基于径向基函数神经网络的高聚物粘结炸药切削表面粗糙度预测研究

唐贤进，张丘，邹刚，吴松，刘维，尹锐

(中国工程物理研究院 化工材料研究所，四川 绵阳621900)

0 引言

高聚物粘结炸药(PBX)是由粘弹性的粘结剂和硬脆性的炸药颗粒混合填充的一种复合材料。PBX炸药的表面质量直接影响着其刚度、疲劳强度、老化度、装配质量以及形位尺寸精度等状态参数，从而最终影响着武器系统的有效性和可靠性［1-2］。而表面粗糙度是评价表面质量的重要指标，也是切削工艺参数对PBX 炸药作用的重要反馈结果。因此，研究PBX 炸药表面粗糙度对于优化切削工艺参数，提高炸药及武器部件的性能有着重要的现实意义。

国内外一些学者通过扫描电子显微镜和原子力显微镜观测了不同PBX 炸药材料的微观形貌并取得了一些成果。Baer［3］利用光学显微镜和电子扫描显微镜分析了HMX(奥克托今)、TATB(1，3，5-三氨基-2，4，6-三硝基苯)、PETN(太安)等炸药晶体的微观形貌。Proud 等［4］利用原子力显微镜分析了纯炸药晶体对粘结剂的增强作用。李明等［5］定量分析了一种TATB 基的PBX 炸药损伤变形局部化特征。唐维等［6］采用轮廓仪测量了某PBX 的车削表面，并推导了粗糙度与车削深度、进给量和机床主轴转速的经验公式。张丘等［1］分析了二维评定法和三维评定法对表面粗糙度评定的差异及其原因。然而，上述研究局限在PBX 炸药表面或者断口的微观形式以及形成机理，缺乏将影响PBX 炸药切削表面粗糙度的多因素综合考虑的定量分析。

人工神经网络由于具有非线性映射能力、自组织和自学习的特性，其在机械加工领域的应用越来越广泛［7］，尤其是在解决加工表面粗糙度的预测［8］。加工过程中切削参数的优化以及加工机床实时误差补偿与控制［9］等这类非线性、数据量大、多因素混杂的问题，人工神经网络表现出了独特的优势。因此，本文利用表面三维轮廓测量仪对PBX炸药切削表面数据观测分析的基础上，分析了PBX炸药切削表面成形的原因以及二维粗糙度评价的误差，通过径向基函数(RBF)人工神经网络建立了PBX 炸药切削表面粗糙度的预测模型，并给出了预测结果以及预测误差。

1 实验

1.1 材料与仪器

材料采用某TATB 基PBX 炸药。机床为NEF400 卧式数控车床。刀具为r =0.2 mm 菱形车刀，刀片牌号为CCGX060202-AL.主偏角Kr=95°和r=5 mm 圆弧车刀，刀片牌号RCGX0803M0-AL.表面三维轮廓测量仪采用NANOVEA PS50 光学轮廓仪。

1.2 实验方法

试样制备:通过对实验条件的分析，选取刀具半径、主轴转速、进给率和切削深度4 个因素来考察切削工艺参数对PBX 炸药切削表面粗糙度的影响。结合PBX 炸药加工的工艺特点，以及加工工艺参数的优化，选取如表1所示不同切削工艺参数的数值。在干切削的状态下，将PBX 炸药柱加工到尺寸为φ40 mm×10 mm，共制得PBX 药柱样品70 个，140 个检测端面。

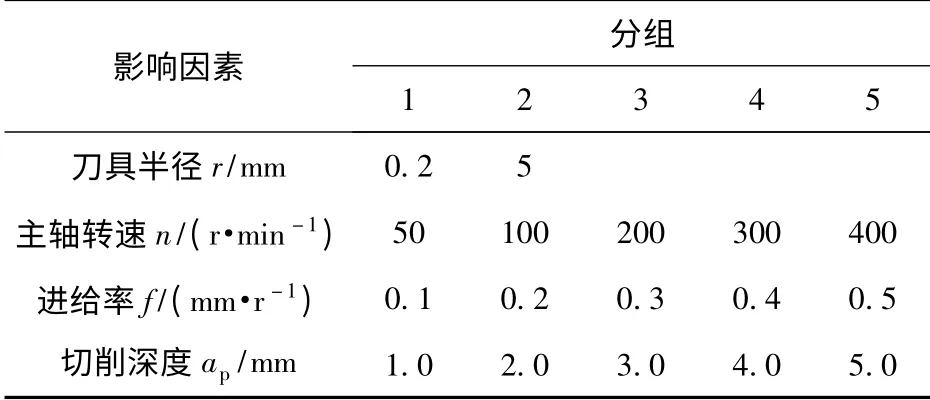
表1 PBX 车削实验表面粗糙度影响因素Tab.1 Suface roughness influence factors of PBX in turning experiment

测量方法:采用非接触式NANOVEA PS50 光学轮廓仪进行测量，如图1所示。其x、y 向分辨率为0.1 μm，z 向垂直分辨率5 nm，z 向精度60 nm.并设置z 向径深量程为400 μm，测量的x、y 表面面积为4 mm×3 mm，采样间距10 μm.

图1 表面三维轮廓测量仪Fig.1 3D contour measuring meter

2 实验结果与分析

2.1 测量结果

通过NANOVEA PS50 光学轮廓仪对140 个PBX 药柱切削表面进行了测量，得到了140 幅切削表面的三维图像以及三维轮廓坐标值。并选取了4组(见图2(a)～图2(d))典型切削工艺参数下的测量图像，如图2所示，图中对明显的崩落处用白色圆圈进行了描绘。

2.2 形貌分析

PBX 药柱在进行端面车削时，切削表面的形成过程其实就是刀具的径向进给运动与药柱的旋转运动的合成，以及PBX 炸药的表面材料不断地被挤压和剪切而断裂形成切屑的过程［1］。如图1所示，由于刀具的副偏角K＇r不可能为0°，因此在切削表面就会形成变径圆弧螺旋线式的残留面积(图3中阴影部分)。而在实际加工中，由于受机床振动、刀具磨损、PBX 炸药材料本身特性等诸多因素的影响，实际切削表面的形貌往往与理论上存在较大差距(图2中圆圈处)。

由于PBX 炸药是由主体炸药和少量粘结剂经过造粒压制后构成的均相颗粒复合材料，在压制过程中，部分炸药晶体颗粒已经受到损伤或破碎［10］。因此，PBX 材料在受刀刃挤压和剪切的作用下，表现为4 种断裂形式:

图2 不同切削工艺参数下PBX 炸药表面形貌观测图像Fig.2 PBX surface morphologies under different process

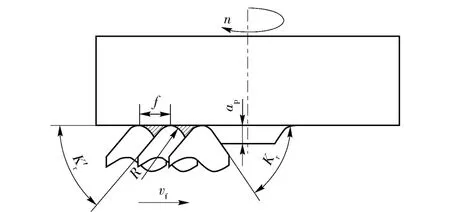
图3 切削表面形貌形成过程Fig.3 Forming process of cutting surface topography

1)炸药晶体被破坏的穿晶断裂;

2)已破碎炸药晶体沿破碎面断裂的孪晶分离;

3)炸药晶体与粘结剂之间的脱落分离;

4)粘结剂被破坏的断裂。

因此，PBX 切削表面的粗糙度由于受切削工艺参数、材料特性、实际工况等诸多因素的影响，很难建立一个涵盖多参数的数学模型来表征其表面粗糙度。然而，通过NANOVEA PS50 光学轮廓仪的观测，可以初步定性地得出3 点结论:

1)由于PBX 炸药经压制粘结而成，在切削表面(见图2(a)～图2(d))总会呈现材料崩落的现象，并且崩落处是随机的;

2)刀具半径越大(见图2(c)、图2(d))，在同等切削参数的情况下，切削表面越光滑，即粗糙度越低;

3)一般来说，主轴转速越快，进给率越低，切削深度越小(见图2(a)、图2(c))，粗糙度越低。

2.3 粗糙度分析

表面粗糙度一般是指加工表面上具有的较小间距和峰谷所组成的微观几何形状特性，其常用的评价参数为Ra(二维轮廓算术平均偏差，μm)。在本文中的车削端面内，二维轮廓是过圆心的径向轮廓，即沿任意刀痕的法向上。其计算表达式为

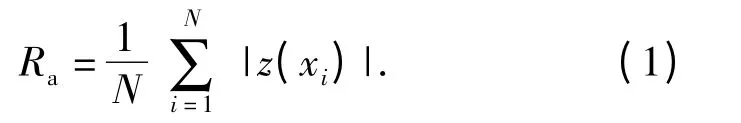
通过2.2 节分析，由于PBX 炸药切削表面的崩落特性，用二维轮廓来评价表面粗糙度势必带来偶然性，在切削表面的不同轮廓下粗糙度不同。因而引入Sa(三维轮廓算术平均偏差，μm)来评价，即整个测量端面内的粗糙度评价值。其计算表达式为

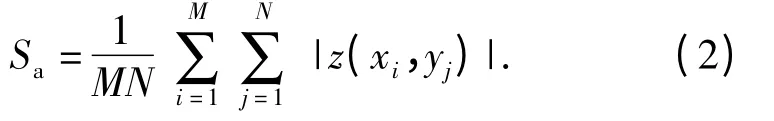
下面通过一具体的PBX 切削表面来考察Ra与Sa的差异。

图4展示了在该切削工艺(r =0.2 mm，n =200 r/min，f =0.3 mm/r，ap=2.0 mm)条件下，PBX切削表面在NANOVEA PS50 光学轮廓仪下的测量图像。该仪器测得在4 mm×3 mm(X-Y)的表面上，Sa的值为9.683 2.并选取图4中的A、B、C、D 四处位置，通过MATLAB 软件绘制出该四处位置的二维轮廓曲线，如图5所示。由于检测面积相对整个PBX 药柱端面极小，未考虑未在A、B、C、D 四处法向位置选线而造成的误差。

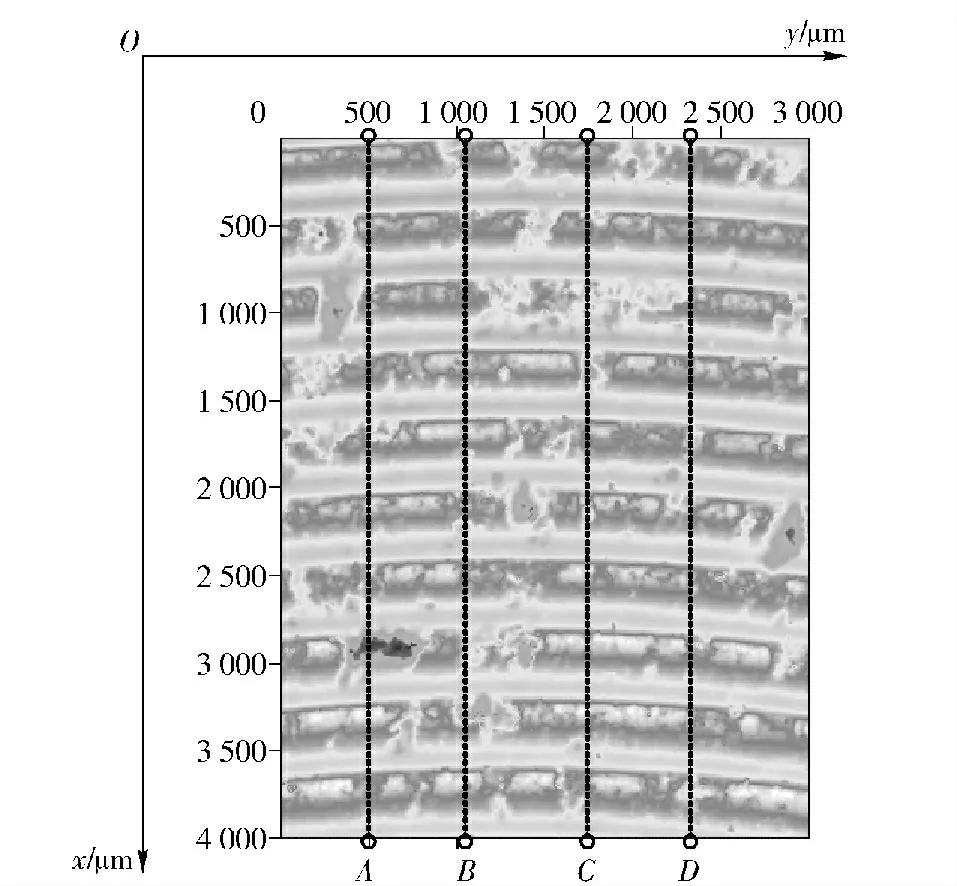
图4 PBX 切削表面形貌观测图(r=0.2 mm，n=200 r/min，f=0.3 mm/r，ap =2.0 mm)Fig.4 PBX surface morphologies

图5中可以明显地看出，在A、B、C、D 四个位置，二维轮廓均不相同，波峰波谷存在显示的差异，相应的Ra也均不相同，分别为14.283 2 μm、12.307 8 μm、13.219 8 μm 和11.514 4 μm.表2还列出了A、B、C、D 四个位置Ra与整个表面Sa的差异。其中η 为相对误差，计算表达式为

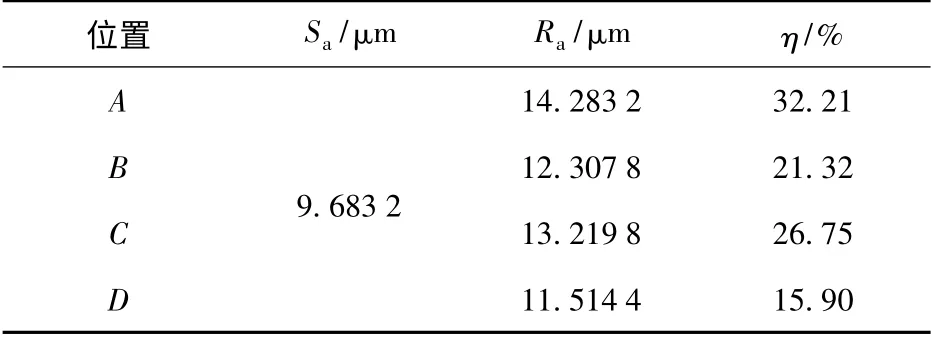
表2 Ra 与Sa 的差异Tab.2 Difference between Ra and Sa

图5 二维轮廓曲线Fig.5 The 2D-contour curves at locations A，B，C and D

因此，通过对PBX 炸药切削表面成形的原因以及二维粗糙度误差分析得出如下结论:PBX 切削表面的形貌受材料特性、切削工艺和切削工况等多重因素影响而具有随机不确定性;单一因素不具备评价PBX 切削表面粗糙度的能力;建立PBX 切削表面粗糙度与影响因素之间的精确数学模型非常困难。为此，本文构建RBF 神经网络预测模型，充分考虑到PBX 表面粗糙度的随机性、非线性和多因混杂的特点。

3 RBF 神经网络预测

3.1 RBF 神经网络设计

RBF 神经网络是一种品质优良的前向网络，具有很强的逼近能力和很快的收敛速度，通过训练RBF 神经网络能够以任意精度近似任意非线性函数［11］。因此本文的PBX 炸药切削表面粗糙度预测模型采用前馈型RBF 神经网络。图6为设计的粗糙度预测模型的神经网络结构。

图6 粗糙度预测模型的神经网络结构Fig.6 Neural network structure of roughness prediction model

图6中的RBF 包含了3 层结构。

第一层输入层，由影响粗糙度的独立变量组成，本文中选取刀具半径r、主轴转速n、进给率f 和切削深度ap4 个变量;而未选取诸如材料和工况直接作为输入，材料和工况对粗糙度的影响正是通过网络的训练学习来表征。

第二层为隐含层，采用RBF 作为网络的激活函数，完成输入空间到隐含单元空间的非线性变换;基函数应具有局部感受的特征，并能体现RBF 网络的非线性映射能力，一般取为Gauss 函数。因此，RBF神经网络隐含层第i 个节点的输出为

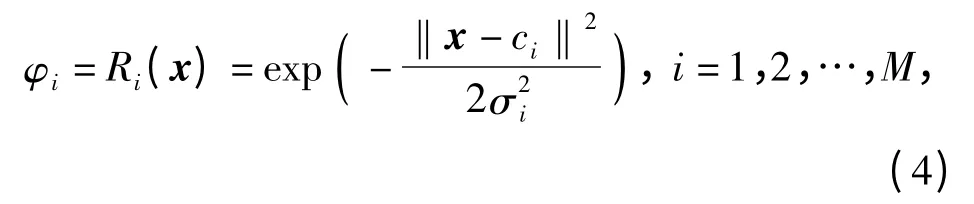
式中:φi为隐含层第i 个节点的输出;Ri(x)为基函数;x 为四维输入向量;ci为第i 个基函数的中心;σi为第i 个基函数的方差;M 为隐含层神经元的个数;‖x-ci‖是向量x -ci的范数，表示x 与ci之间的距离。

第三层为输出层，提供从隐含单元到输出空间的一种线性变换，即输出Sa.

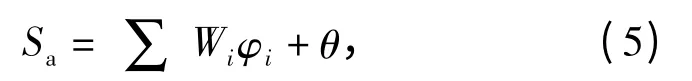
式中:Wi为隐含层第i 个节点与输出层的连接权值;θ 为输出节点的偏移。

3.2 RBF 神经网络训练

设计了神经网络结构之后，需要通过训练样本让神经网络学习，其学习的目的是确定隐含层各个神经元基函数的中心位置ci和方差σi，以及隐含层神经元与输出层之间的连接权值Wi［12］。样本来自于NANOVEA PS50 光学轮廓仪下测得的140 个PBX 药柱切削表面的Sa，并分别以1，2，…，140 进行编号，其中表3列出了PBX 炸药切削表面粗糙度预测模型的部分训练样本(135 个)，表4列出了预测模型的精度检验样本(5 个)。

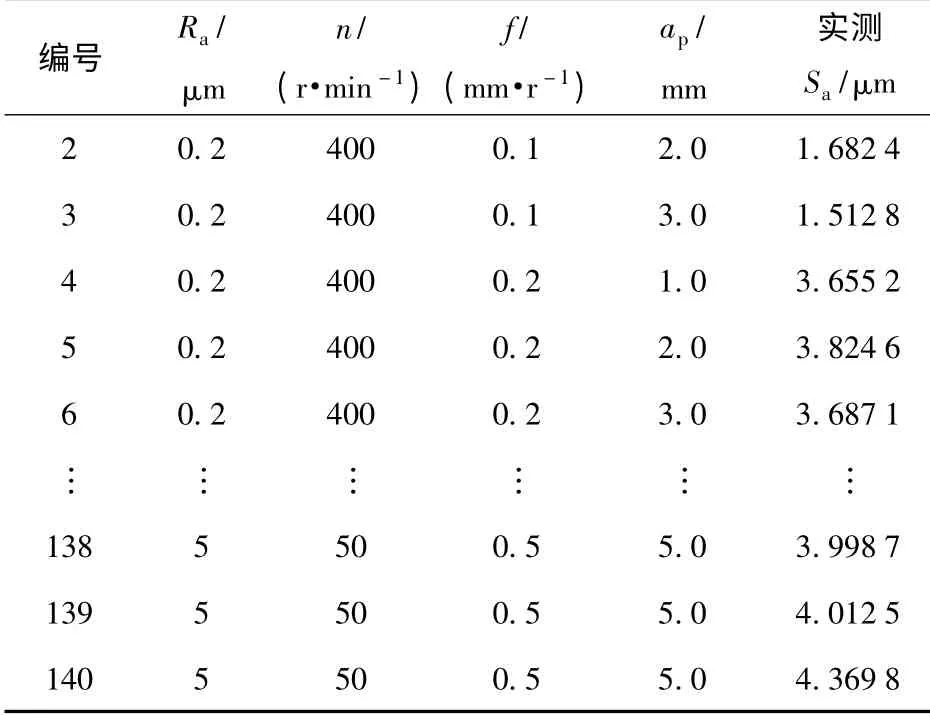
表3 训练样本Tab.3 Training sample

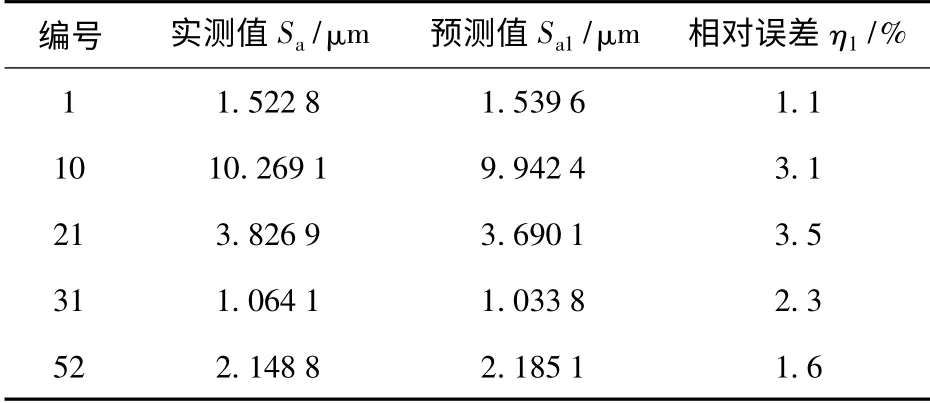
表4 实测值与预测结果比较Tab.4 Comparison of measured results and predicted results

为了提高神经网络的训练效率，对训练样本进行归一化预处理，即将表3中的数据映射到［-1，1］中。使用的归一化公式为

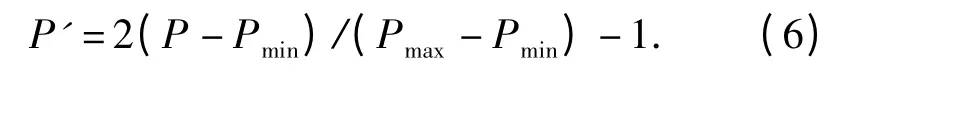
预测完后，还需将数据进行还原，还原公式为

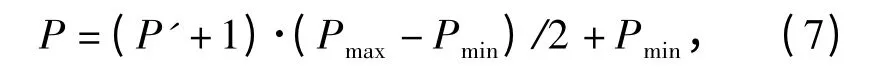
式中:P 为样本原始数据;Pmin为样本中的最小值;Pmax为样本中的最大值;P'为归一化预处理后的数据。

一般地，RBF 神经网络的学习过程分为两个阶段:

第一阶段:采用NSL(自组织学习)确定RBF 的中心和方差。

第一步:初始化基函数中心，从训练样本集中随机选取M 个不同的样本作为初始化中心ci(0)i =1，2，…，M.

第二步:随机输入训练样本xk.

第三步:寻找离xk最近的中心i(xk)，k =1，2，…，45，使其满足

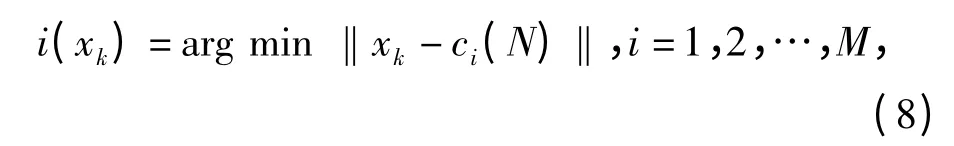
式中:ci(N)为第N 次迭代时的基函数第i 个中心。第四步:调整中心，使其满足

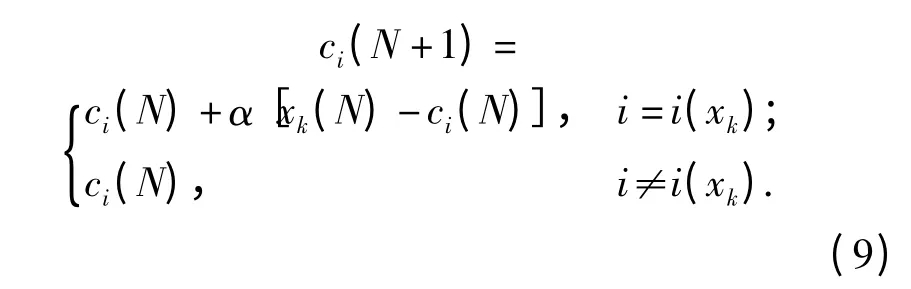
式中:α 为学习速率，满足0 ＜α ＜1.

第五步:判断是否学完所有的样本且中心分布不再变化，否则N=N+1，转到第二步。

最后得到RBF 网络最终的基函数中心ci，i=1，2，…，M.

当隐含层各神经元的基函数中心确定以后，由于选取的是Gauss 函数，所以方差σi可由下式确定。

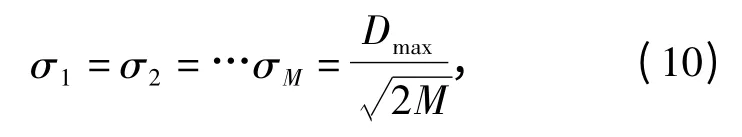
式中:Dmax为所选取中心之间的最大距离。

第二阶段:采用SL(监督学习)确定隐含层与输出层之间的连接权值。

第一步:初始化连接权值Wi(0)，i=1，2，…，M，计算隐含层单元的输出:

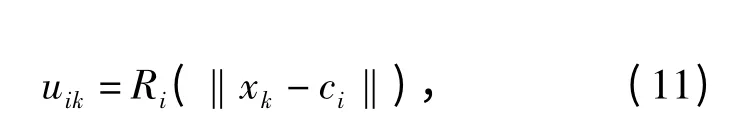
式中:uik为隐含层第i 个神经元的输出;Ri为隐含层第i 个神经元的基函数;ci为隐含层第i 个神经元的基函数中心。

第二步:计算网络的输出

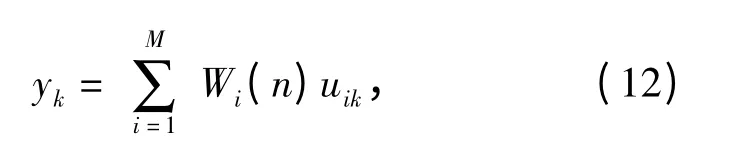
第三步:计算输出结果的误差

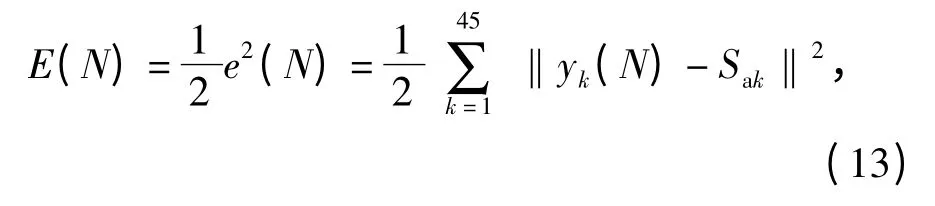
式中:E(N)为第N 次迭代的误差;Sak为第k 个实际Sa的测量值。

第四步:判断误差是否满足要求，否则调整连接权值，重新计算。

式中:β 为学习算子，满足0 ＜β ＜1.

最终得到RBF 网络最终的连接权值Wi，i =1，2，…，M.

3.3 训练结果与验证

选择刀具半径r、主轴转速n、进给率f 和切削深度ap作为网络输入层节点，以及已加工PBX 切削表面的实测Sa作为网络的期望输出。依据3.1 节和3.2 节确定的模型，运用MATLAB 编制算法程序进行训练，其网络训练误差如图7所示。

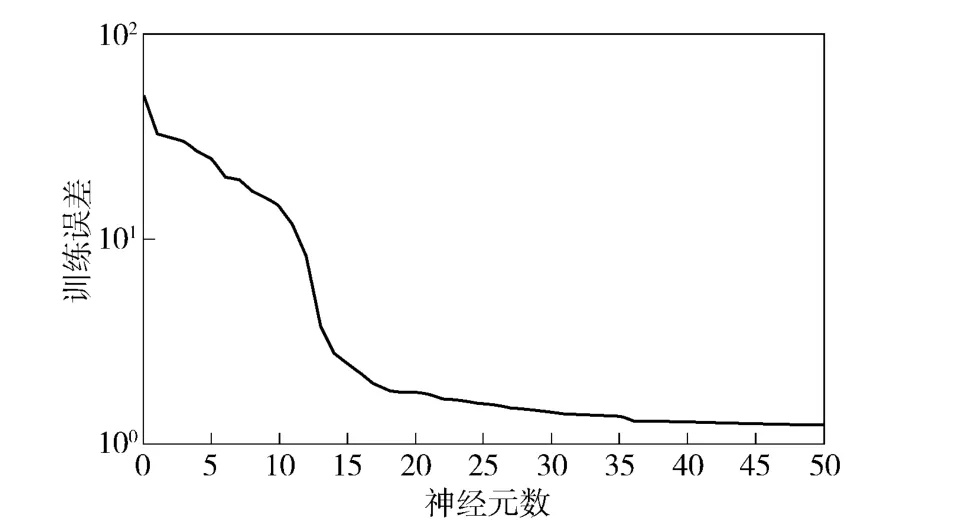
图7 网络训练误差图Fig.7 Error graph of training neural network

从图7中可以看出，随着神经元个数的增加，训练误差在逐步减小，表明了预测的期望值在逐渐地逼近实测值，当误差达到10-3数量级时，训练终止。为了验证构造的预测网络泛化能力，选取了5 个样本来检验训练精度。如表4所示。当中，Sa为实际检测值，Sa1为预测值，η1为实测值与预测值之间的相对误差。结果显示，预测的最大误差不超过3%，表明了文中所建预测模型的合理与正确。如果有足够多的训练样本，预测的误差会更小。

4 结论

PBX 切削表面的形貌因为受到诸多因素的影响而具有随机不确定性，因此Ra不具备评价整个PBX 切削表面粗糙度的能力，同时要建立PBX 切削表面三维粗糙度与影响因素之间的精确数学模型非常困难。

由RBF 神经网络构建的PBX 炸药切削表面粗糙度预测模型，考虑了PBX 炸药表面粗糙度的随机性、非线性和多因混杂的特点。通过对RBF 神经网络预测模型的训练和验证，表明该模型基本上能够反映切削表面成形的基本规律，也能够较好地预测PBX 切削表面的三维粗糙度。

References)

［1］ 张丘，黄交虎，尹锐，等.高聚物粘结炸药切削表面的细观形貌与形成机理［J］.兵工学报，2010，31(10):1337 -1340.ZHANG Qiu，HUANG Jiao-hu，YIN Rui，et al.Micro-appearance and formation mechanisms of PBX cutting surface［J］.Acta Armamentarii，2010，31(10):1337 -1340.(in Chinese)

［2］ 罗景润.PBX 的损伤、断裂及本构关系研究［D］.绵阳:中国工程物理研究院，2001.LUO Jing-run.Study on damage，fracture and constitutive relation of PBX［D］.Mianyan:China Academy of Engineering Physics，2001.(in Chinese)

［3］ Baer M R.Modeling heterogeneous energetic materials at the mesoscale［J］.Thermochinica Acta，2002，384:351 -367.

［4］ Proud W G，Palmer S J P，Field J E，et al.AFM studies of PBX systems［J］.Thermochinica Acta，2002，384(1/2):245 -251.

［5］ 李明，张珏，李敬明，等.高聚物粘结炸药压缩破坏的细观力学实验研究［J］.含能材料，2005，13(2):79 -84.LI Ming，ZHANG Yu，LI Jing-ming，et al.Experimental investigation to the damage localization of PBX mechanical failure at mesoscale［J］.Energetic Materials，2005，13(2):79 -84.(in Chinese)

［6］ 唐维，李明，黄交虎，等.PBX 车削表面的细观形貌与粗糙度研究［J］.含能材料，2009，17(1):59 -62.TANG Wei，LI Ming，HUANG Jiao-hu，et al.Study on turning surface micro-morphology and roughness of PBX parts［J］.Chinese Journal of Energetic Materials，2009，17(1):59 -62.(in Chinese)

［7］ 师汉民，陈吉红，阎兴，等.人工神经网络及其在机械工程领域中的应用［J］.中国机械工程，1997，8(2):5 -10.SHI Han-min，CHEN Ji-hong，YAN Xing，et al.Artificial neural network and its application in the field of mechanical engineering［J］.China Mechanical Engineering，1997，8(2):5 -10.(in Chinese)

［8］ 李晓梅，丁宁，朱喜林.表面粗糙度模糊神经网络在线辨识模型［J］.机械工程学报，2007，43(3):212 -217.LI Xiao-mei，DING Ning，ZHU Xi-lin，et al.On-line identification model of surface roughness based on fuzzy-neural nnetwork［J］.Chinese Journal of Mechanical Engineering，2007，43(3):212 -217.(in Chinese)

［9］ 张毅，杨建国.基于灰色神经网络的机床热误差建模［J］.上海交通大学学报，2011，45(11):1581 -1586.ZHANG Yi，YANG Jian-guo.Grey neural network modeling for machine tool thermal error［J］.Journal of Shanghai Jiaotong University，2011，45(11):1581 -1586.(in Chinese)

［10］ 梁华琼，周旭辉，唐常良，等.HMX 钢模压制的微观结构演变研究［J］.含能材料，2008，16(2):188 -190.LIANG Hua-qiong，ZHOU Xu-hui，TANG Chang-liang，et al.Microstructural evolution of HMX during pressing［J］.Chinese Journal of Energetic Materials，2008，16(2):188 - 190.(in Chinese)

［11］ Skaf Z，Wang H，Guo L.Fault tolerant control based on stochastic distribution via RBF neural networks［J］.Journal of Systems Engineering and Electronics，2011，22(1):63 -69.

［12］ 刘岗.精密车削表面粗糙度预测及切削参数优化研究［D］.秦皇岛:燕山大学，2009.LIU Gang.Predication for surface roughness and optimization of cutting parameters in precision turning［D］.Qinhuangdao:Yanshan University，2009.(in Chinese)