一种新的线性调频脉冲信号参数估计算法

陈磊，陈殿仁，刘颖

(长春理工大学 电信学院，吉林 长春130022)

0 引言

近年来，在雷达信号处理领域，线性调频(LFM)脉冲信号参数检测和估计受到广泛关注［1］。多种信号处理技术被应用于LFM 脉冲信号的的参数检测和估计算法中，包含功率谱估计、Wigner-Ville 分布、Choi-Williams 分布等方法的非线性时频变换技术，用来产生信号的时频图像，进而分析信号瞬时频率随时间的变换情况［2］。邓兵等［3］分析了基于分数阶傅里叶变换的LFM 脉冲时延估计特性。刘锋等［4］提出了一种基于联合Wigner-Ville 分布-随机Hough 变换改进算法的LFM 信号参数快速估计方法;陈鹏等［5］研究了一种基于离散分数阶傅立叶变换的水下动目标线性调频回波检测算法;罗洁思等［6］研究了一种基于多尺度LFM 基信号稀疏分解的多分量LFM 信号检测方法。刘建成等［7］在研究目标径向速度估计算法时采用了Wigner-Hough变换。

Wigner-Ville 分布可有效地用于单分量的LFM信号参数估计，但是在多分量信号的场合交叉项会干扰信号中心频率和调频率的估计;平滑伪Wigner-Ville 分布(SPWVD)和时频分布级数(TFDS)法可以有效的抑制交叉项的影响，但是会降低估计参数的频率分辨率［8］;Wigner-Ville-Hough 变换(WVHT)在针对单分量LFM 脉冲信号参数估计时会有较好的效果，但是在多分量多周期LFM 脉冲信号的参数估计时会出现多个峰值，并且在低信噪比环境中增加观察时间，WVHT 输出信号的信噪比不会有所提高，这就会影响信号初始频率和调频率的检测和估计性能［9］。本文提出一种基于周期Wigner-Ville-Hough变换(PWVHT)的LFM 脉冲信号的参数估计算法，在进行单分量LFM 脉冲信号参数估计时此算法和WVHT 具有相同的优点，在进行多分量LFM 脉冲信号参数估计时该算法在时间域内对周期和脉宽进行搜索，然后将信号处理结果进行折叠加权，一方面提高了信号真值处的信噪比，另一方面避免了WVHT在进行多分量LFM 脉冲信号参数估计时会出现的交叉项干扰。通过分析和仿真表明，与WVHT 相比，在进行多脉冲分量和多周期参数估计时，PWVHT 性能更优。

1 LFM 脉冲信号的PWVHT

1.1 LFM 脉冲信号的数学模型

在LFM 脉冲信号中，第m 个LFM 脉冲信号的数学表达式为

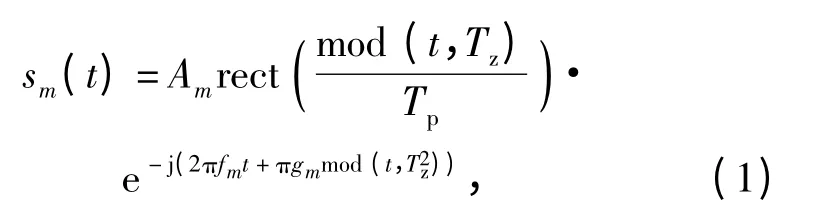
式中:Am为信号幅值;fm为信号初始频率;Tz为脉冲重复周期;Tp为脉冲宽度;gm为信号的调频率，gm=Bm/Tp;t 为时间变量;re ct为矩形信号，且

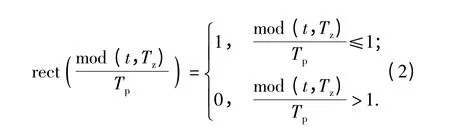
对信号进行离散化之后得到的雷达信号序列可表示为

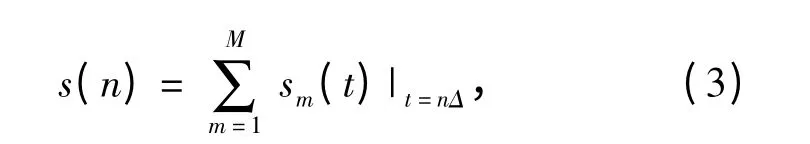
式中:n 为雷达离散信号序列号;M 为LFM 脉冲个数;Δ 为采样周期，Δ=1/fs，fs为采样频率。

本文所讨论的LFM 脉冲信号的任一个重复周期内参数Am、fm、gm、Tz、Tp均相同。

1.2 PWVHT

Wigner-Ville 分布(WVD)是二次时频变换方法中最基本的一种，广泛应用于雷达信号分析领域［10］，离散信号x(n)的WVD 定义为

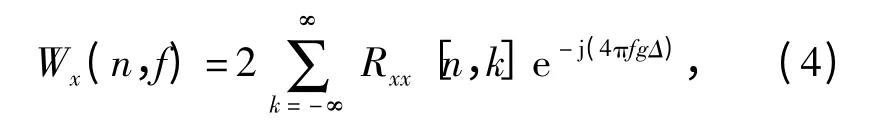
式中:Rxx(n，k)为x(n)的自相关函数，Rxx(n，k)=x［n+k］x*［n -k］;n 为离散信号的序列号，n =0，1，2，…，N-1(N 为离散信号x(n)的长度);k 为时移变量;Δ 为信号的采样周期。

WVHT 算法通常使用于LFM 信号参数估计场合中，其作用是在WVD 变换后的时频图像中搜索直线，文献［11］给出了LFM 信号的WVHT 变换为

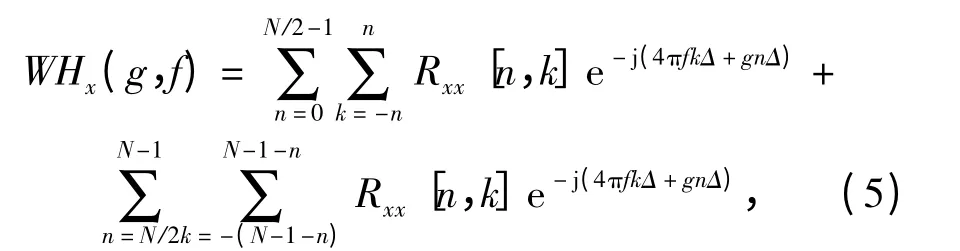
式中:f 为信号初始频率;g 为信号的调频率。

在WVHT 后的(g，f)二维空间内，当g =g1，f =f1(g1，f1为待估计信号的参数准确值)时，WHx(g，f)会出现峰值［12］。

假设一LFM 脉冲信号参数为f1=10 MHz，Tp=10 ms，g1=400 MHz/s，采样周期Δ =10 ns，当信噪比为-10 dB，脉冲个数M=2 时其WVHT 的Matlab仿真如图1所示。

当样本信号中含有2 个脉冲分量时，WVHT 结果中会出现2 个峰值，大小均为1.5×104。当样本信号中含有M 个分量LFM 脉冲时(M≥2)，WVHT图中会出现M 个峰值，且峰值的幅值相同，说明WVHT 峰值只由对应的脉冲内的样本数据计算得到。通过此峰值可以检测出样本信号的起始频率f1和调频率g1.

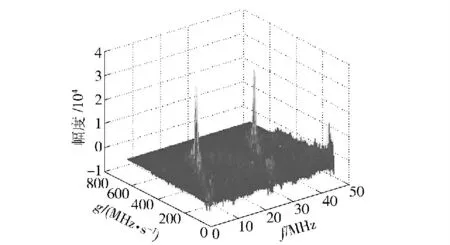
图1 多LFM 脉冲分量信号的WVHTFig.1 WVHT of chirp signal composed of multiple pulses

在噪声环境中，假设样本信号x(n)=s(n)+w(n)，n =0，1，…，K -1，且信噪比为SNRi，其中w(n)是均值为0、方差为σ2v的高斯噪声。则样本信号x(n)经过WVHT 后输出信号Wx(g，f)在峰值(f1，g1)处的信噪比［12］可以表示为

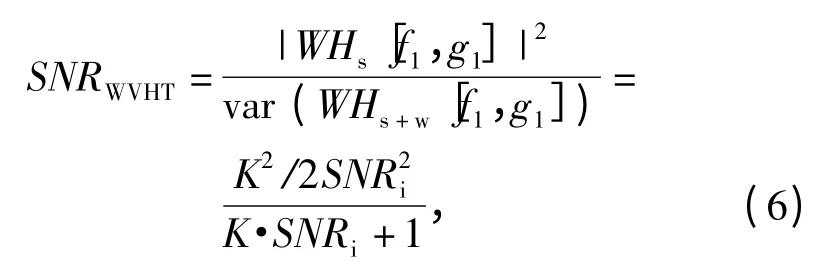
式中:var(WHs+w［f1，g1］)为WHs+w［f1，g1］的方差;WHs［f1，g1］为无噪声干扰的单LFM 脉冲分量信号的 WVHT 在准确估计值(f1，g1)处的值;WHs+w［f1，g1］为噪声干扰下的样本信号WVHT 在准确估计值(f1，g1)处的值;K 为样本信号长度。

由于WVHT 中的任何一个峰值由对应脉冲的样本数据计算得到，则(6)式中K≤Tz/Δ，即WVHT后的输出信噪比不会大于((Tz/Δ)2/2)SNR2i/((Tz/Δ)SNRi+1).因此，WVHT 并非最优的多分量LFM脉冲参数估计方法，因为WVHT 并没有有效地利用所有样本数据信息。当样本观察时间大于一个脉冲周期时，WVHT 输出信噪比并不会因为观察时间的增加而变大;当样本信号信噪比非常小时，图1中的峰值有可能被淹没在噪声中，则无法进行信号的检测和参数估计。由于每个峰值信号的参数都是相同的，如果将这些数据进行折叠相加，可以进一步对噪声进行压缩，提高峰值点的幅值，即提高输出信噪比。

基于这种思想，针对观察信号x(n)，n =0，1，2，…，N-1，令其PWVHT 为

式中:Ω 为待估参数，Ω =(f，g);F［n，k］为匹配函数，且

多分量(M ＞1)LFM 脉冲信号的PWVHT 为

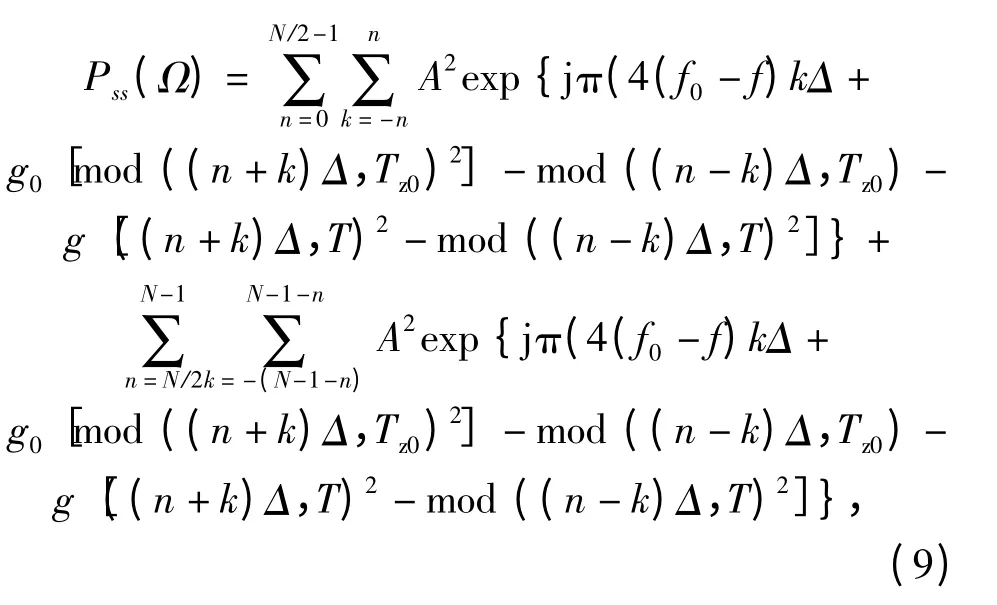
式中:n=0，1，…，N-1(N=M×Tz/Δ);信号中的矩形窗只影响上式中的求和区间。假设在Ω0=(f0，g0，Tp0，Tz0)处Pss［n，k］取最大值，则

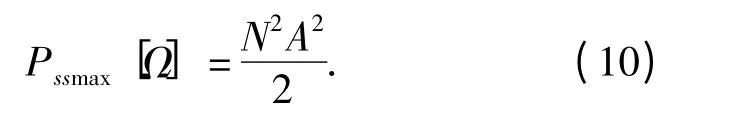
采用1.2 节中相同参数的样本信号进行PWVHT 仿真，结果如图2所示。

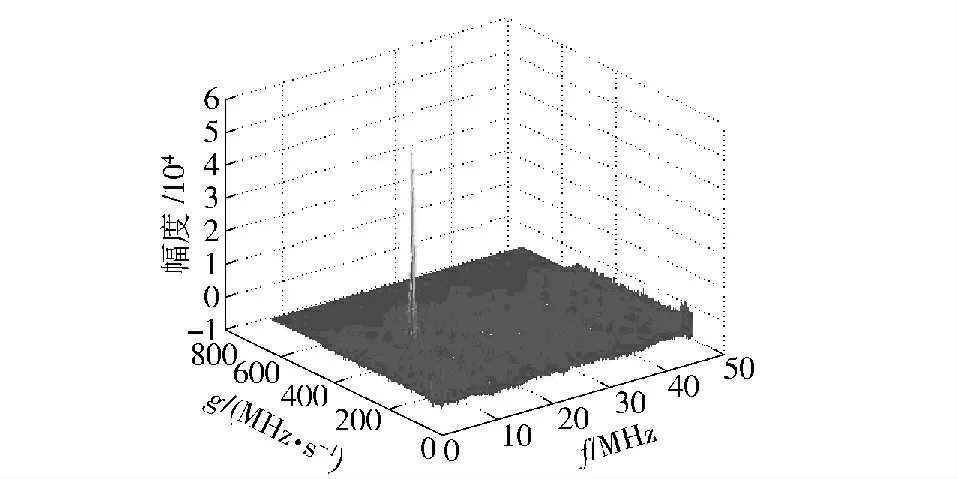
图2 多LFM 脉冲分量信号的PWVHTFig.2 PWVHT of chirp signals composed of multiple pulses

通过PWVHT 运算，图中只出现一个峰值点，幅值为2.9×104，为图1中单个峰值幅度的2 倍。参考(11)式和(6)式，K =N/2，这个仿真结果是正确的。

1.3 参数计算

根据(9)式和图2可知，多分量LFM 脉冲信号的PWVHT 出现一个峰值点，该峰值点的横坐标为LFM 真实频率f0的估计值，纵坐标为调频率的估计值g0.

因此，PWVHT 多分量LFM 脉冲信号参数估计算法实现流程如下:

1)对回波信号进行如(10)式PWVHT;

2)搜索变换结果，并获得峰值点处的横坐标和纵坐标;

3)横坐标为LFM 起始频率f0的估计值，纵坐标为调频率g0的估计值。

2 PWVHT 性能分析

2.1 输出信噪比分析

在噪声环境中，假设样本信号x(n)=s(n)+v(n)的信噪比为SNRi，其中n =0，1，2，…，N -1，v(n)是均值为0、方差为σ2v 的高斯噪声，则样本信号x(n)经过PWVHT 后输出信号Px(Ω)的信噪比可以表示为

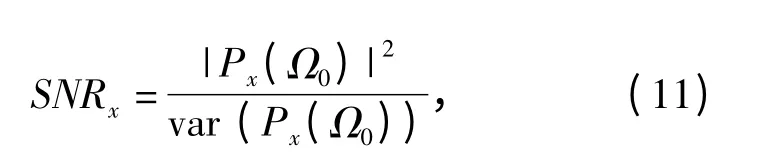
式中:var(Px(Ω))为Px(Ω)的方差，可表示为

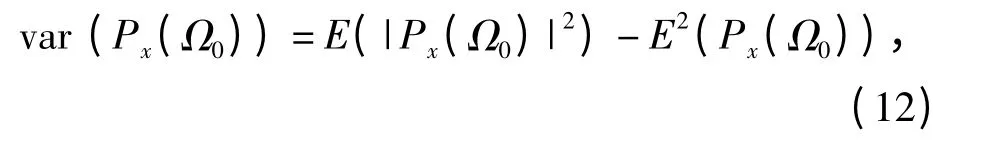
其中:

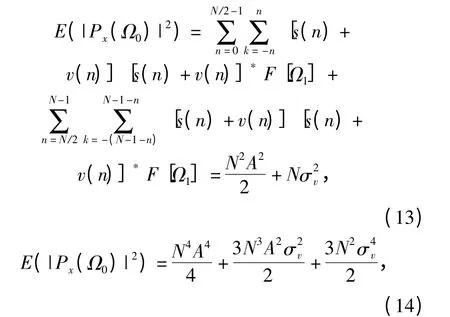
式中:A 为样本信号中LFM 脉冲信号分量的幅度。噪声信号v(n)的自相关函数

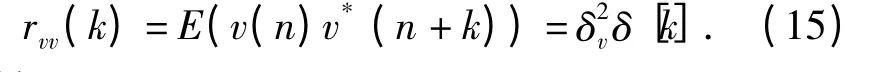
所以

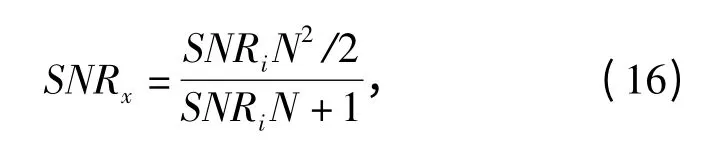
式中:N=MTz/Δ.

由(16)式和N 的取值可以看出，当样本观察时间小于等于一个脉冲周期时，WVHT 和PWVHT 具有相同的输出信噪比。当样本观测时间大于一个脉冲周期时，WVHT 的输出信噪比不会再增大，而PWVHT 输出信噪比随着观测时间的增加继续增加。如图3所示，对f1=10 MHz，Tz=10 ms，g1=400 MHz/s，采样周期Δ=10 ns，信号信噪比为-20 dB，观察时间为30 ms 样本信号的WVHT 与PWVHT 输出信噪比进行了仿真。样本信号WVHT 后的输出信噪比在观察时间达到10 ms 时不再增加，而经过PWVHT 输出的信噪比仍然随着观察时间增加继续变大。

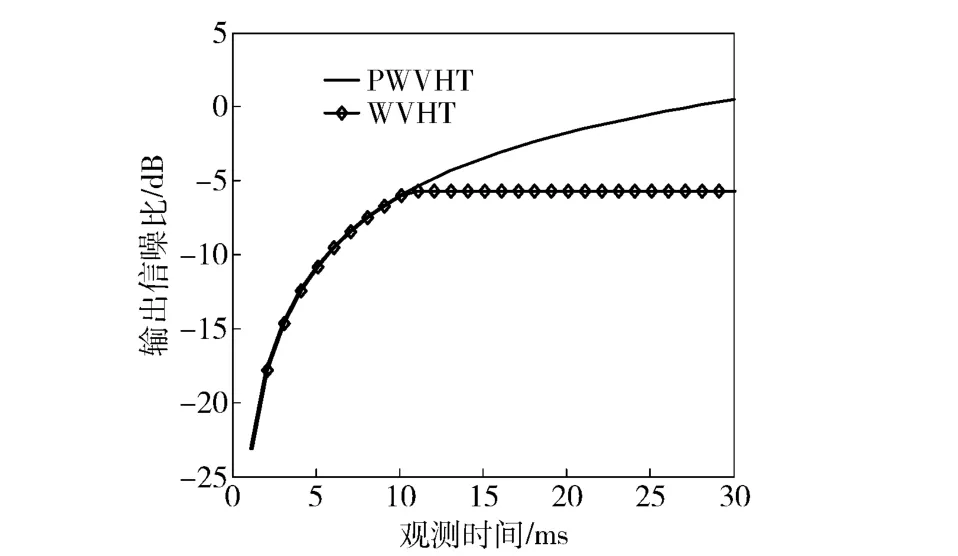
图3 WVHT 与PWVHT 输出信噪比与观察时间的关系Fig.3 The relationship between observation time and output SNR of WVHT and PWVHT

2.2 参数估计精度分析

假设在白噪声v(n)干扰情况下样本信号x(n)= s(n)+ v(n)的PWVHT 中的干扰项为δP(Ω)，则

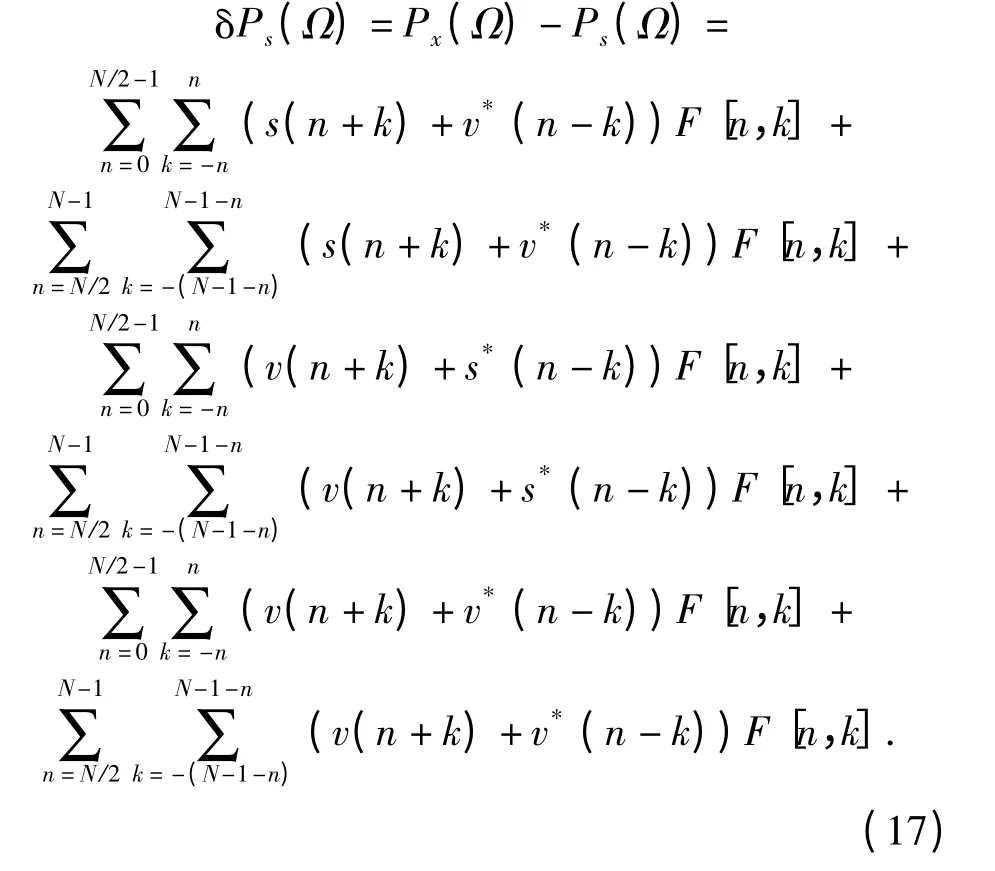
由(17)式可以看出，随着δPs(Ω)的引入，PWVHT 后的峰值点移动到点(f0-δf，g0+δg)处，则Px(Ω)对f 和g 的一阶偏导数在(f0-δf，g0+δg)的取值为0，则

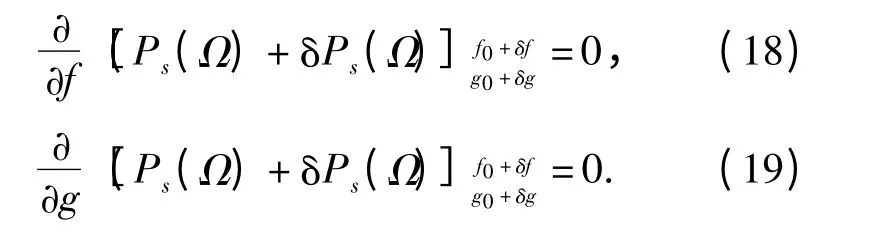
将Ps(Ω)+ δPs(Ω)用泰勒公式将展开，则(18)式和(19)式可写成

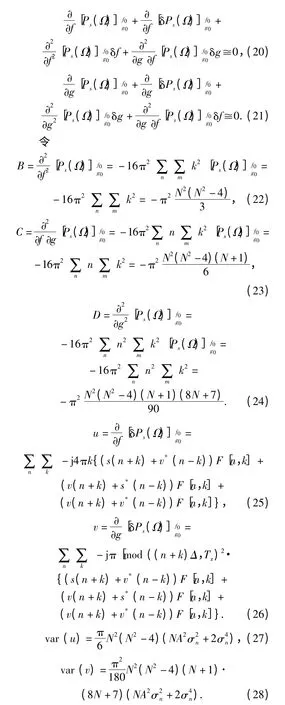
u，v 与噪声v(n)有关，则

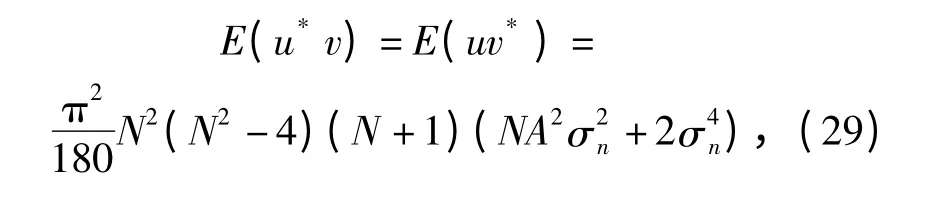
且有

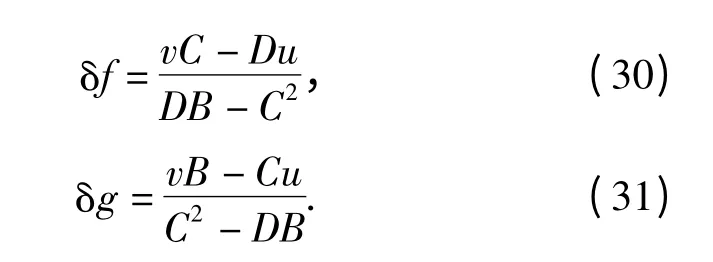
根据(30)式和(31)式，有

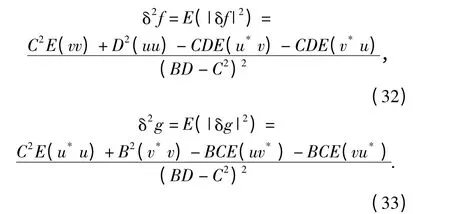
将(22)式～(26)式和(29)式分别带入(32)式和(33)式，可以得到

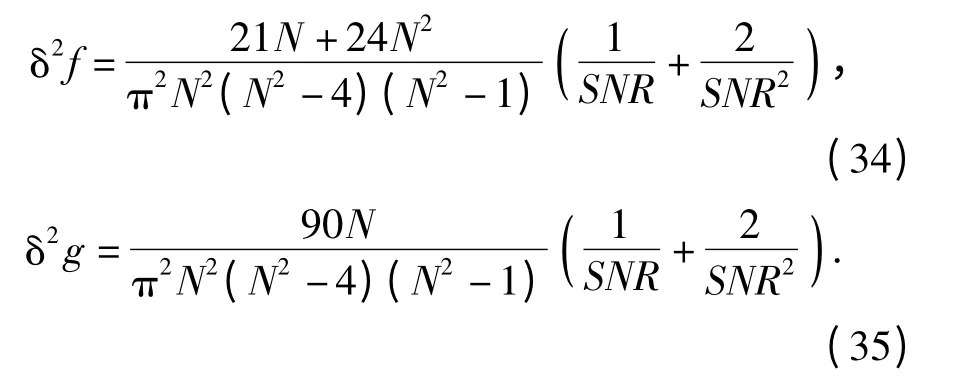
根据(34)式和(35)式，可以得到参数估计均方误差函数与输入信号信噪比和观察时间之间的关系，图4为N=16 时估计均方误差与输入信噪比的关系，图5为估计均方误差与样本观察时间的关系。

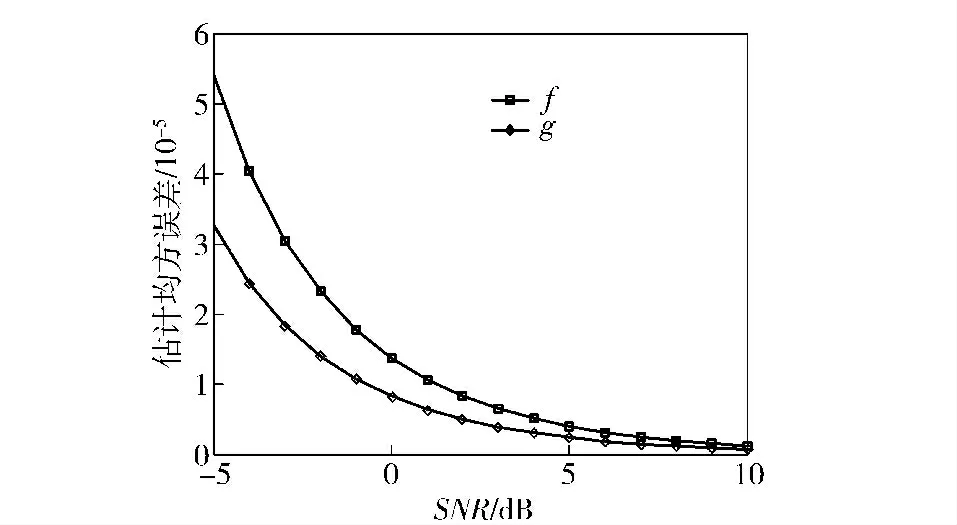
图4 N=16 时估计均方误差与样本信号SNR 的关系Fig.4 The relationship between signal SNR and estimation mean squared error for N=16

由图4和图5可知，当数据长度N 一定时，参数估计误差随着样本数据的SNR 增大而减小，当SNR为定值时，参数估计误差随着观测时间的增长而变小。

2.3 算法仿真分析

针对f1=10 MHz，Tz=30 ms，Tp=10 ms，g1=400 MHz/s，采样周期Δ =10 ns，SNR 分别为-5 dB和-10 dB，观测时间为140 ms 的信号经行500 次PWVHT，取其均值和方差，结果如图6(a)～图6(d)所示。

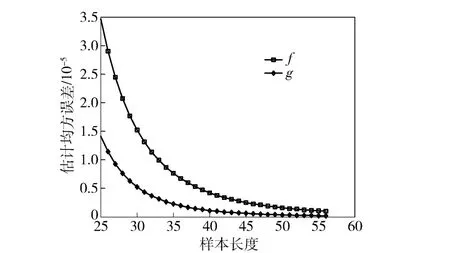
图5 SNR= -10 dB 时估计均方误差与样本长度的关系Fig.5 The relationship between sample length and estimation mean square error for SNR= -10 dB

由图6可知，当观察时间很小时，f 和g 的估计参数会出现偏差，这说明当时间搜索域没有达到最优时，估计结果会出现误差，也就是说，可以通过增加观察时间来提高参数的估计准确性，同时说明PWVHT 和最大似然估计一样，属于渐进有效估计算法。

3 结论

本文在分析了各种不同的LFM 脉冲信号参数估计算法优缺点的前提下，研究了一种基于PWVHT 的LFM 脉冲信号参数估计算法，得到了以下结论:

2)在高斯噪声环境中，采用PWVHT 进行多分量LFM 脉冲信号参数估计时，信号起始频率和调频率的估计均方误差分别为和是样本信号信噪比SNR 和样本长度N 的函数。

3)当样本长度N 很小时，起始频率f 和调频率g 的估计值会出现偏差，这说明当时间搜索域没有达到最优时，估计结果会出现误差，也就是说，可以通过增加观察时间来提高参数的估计准确性，同时说明PWVHT 和最大似然估计一样，属于渐进有效估计算法。

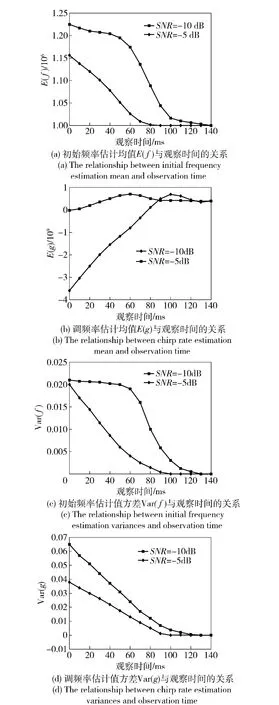
图6 参数估计结果与信号观察时间的关系Fig.6 The relationship between estimation results and signal observation time

4)在进行多分量LFM 脉冲信号参数估计时，PWVHT 不但提高了信号真值处的信噪比，还在不影响估计参数的频率分辨率的前提下，解决了WVHT 在进行多分量LFM 脉冲信号参数估计时会出现的交叉项干扰问题。

References)

［1］ 温景阳，张焕宇，王越.线性调频脉冲压缩雷达参数估计方法［J］.北京理工大学学报，2012，32(7):746 -750.WEN Jing-yang，ZHANG Huan-yu，WANG Yue.Parameters estimation algorithm of LFM pulse compression radar signal［J］.Transactions of Beijing Institute of Technology，2012，32(7):746 -750.(in Chinese)

［2］ Geroleo F G，Brandt-Pearce M.Detection and estimation of multipulse LFMCW radar signals［C］∥Radar Conference.Washington，DC:IEEE，2010:1009 -1013.

［3］ 邓兵，王旭，陶然.基于分数阶傅里叶变换的线性调频脉冲时延估计特性分析［J］.兵工学报，2012，33(6):764 -768.DENG Bing，WANG Xu，TAO Ran.Performance analysis of time delay estimation for linear frequency-modulated pulse based on fractional Fourier transform［J］.Acta Armamentarii，2012，33(6):764 -768.(in Chinese)

［4］ 刘锋，孙大鹏，黄宇.基于联合Wigner-Ville 分布随机Hough 变换改进算法的线性调频信号参数快速估计［J］.兵工学报，2009，30(12):1642 -1646.LIU Feng，SUN Da-peng，HUANG Yu.Fast parameter-estimation of LFM signal based on improved combined WVD and randomized Hough transform［J］.Acta Armamentarii，2009，30(12):1642 -1646.(in Chinese)

［5］ 陈鹏，侯朝焕，梁亦慧.基于离散分数阶傅立叶变换的水下动目标线性调频回波检测算法的研究［J］.兵工学报，2007，28(7):834 -838.CHEN Peng，HOU Chao-huan，LIANG Yi-hui.Research on discrete fractional Fourier transform-based detection algorithm for LFM echo of underwater moving target［J］.Acta Armamentarii，2007，28(7):834 -838.(in Chinese)

［6］ 罗洁思，于德介，彭富强.基于多尺度线性调频基信号稀疏分解的多分量LFM 信号检测［J］.电子与信息学报，2009，31(11):2781 -2785.LUO Jie-si，YU De-jie，Peng Fu-qiang.Multi-component LFM signals detection based on multi-scale chirplet sparse signal decomposition［J］.Journal of Electronics ＆ Information Technology，2009，31(11):2781 -2785.(in Chinese)

［7］ 刘建成，王雪松，肖顺平，等.基于Wigner-Hough 变换的径向加速度估计［J］.电子学报，2005，33(12):2235 -2238.LIU Jian-cheng，WANG Xue-song，XIAO Shun-ping，et al.Radial acceleration estimation based on Wigner-Hough transform［J］.Acta Electronica Sinica，2005，33(12):2235 -2238.(in Chinese)

［8］ 李亚超，王虹现，邢孟道，等.STTFD 的特性分析及其在线性调频信号参数估计中的应用［J］.电子学报，2009，37(9):2102 -2108.LI Ya-chao，WANG Hong-xian ，XING Meng-dao，et al.The analysis of the characteristic and the method of the parameters estimation of LFM signal based on STTFD［J］.Acta Electronica Sinica，2009，37(9):2102 -2108.(in Chinese)

［9］ Millioz F，Davies M E.Detection and segmentation of FMCW radar signals based on the chirplet transform［C］∥2011 IEEE International Conference on Acoustics，Speech and Signal Processing.Prague，CS:IEEE，2011:1765 -1768.

［10］ 王宏禹，邱天爽，陈喆.非平稳随机信号分析与处理［M］.北京:国防工业出版社，2008:311 -313.WANG Hong-yu，QIU Tian-shuang，CHEN Zhe.Nonstationary random signal analysis and processing［M］.Beijing:National Defense Industry Press，2008:311 -313.(in Chinese)

［11］ Geroleo F G，Brandt-Pearce M.Detection and estimation of LFMCW radar signals［J］.IEEE Transactions on Aerospace and Electronic Systems，2012，48(1):405 -418.

［12］ Barbarossa S.Analysis of multicomponent LFM signals by a combined Wigner-Hough transform［J］.IEEE Transactions on Signal Processing，1995，43 (16):1511 -1515.