基于支持向量机的EO-1 Hyperion遥感图像分类研究

毛学刚，郑 淼，郭文茜，马岩岩，胡俊凯，杨天野

(东北林业大学林学院，黑龙江哈尔滨150040)

1 研究区域概况

塔河县是我国最北部的两个县份之一，大兴安岭地区辖县，位于黑龙江省西北部，地处123°～125°E，52°～53°N，与俄罗斯接壤，黑龙江上游右岸，西与漠河县相邻，南与新林区、呼中区接壤，东与呼玛县毗邻，北隔黑龙江与俄罗斯相望，地理位置如图1所示。边境线长173 km，总面积为14 420 km2。塔河县境内地势呈中间高、两侧低，西高东低的地势。境内地形复杂，植被类型多，分布着不同的土壤，以森林和草甸土为主，树种丰富，森林覆盖率为81%;蓄积量5 340万m3，其中成过熟林蓄积为488万m3，主要树种有樟子松、落叶松、白桦、杨树等10余种。

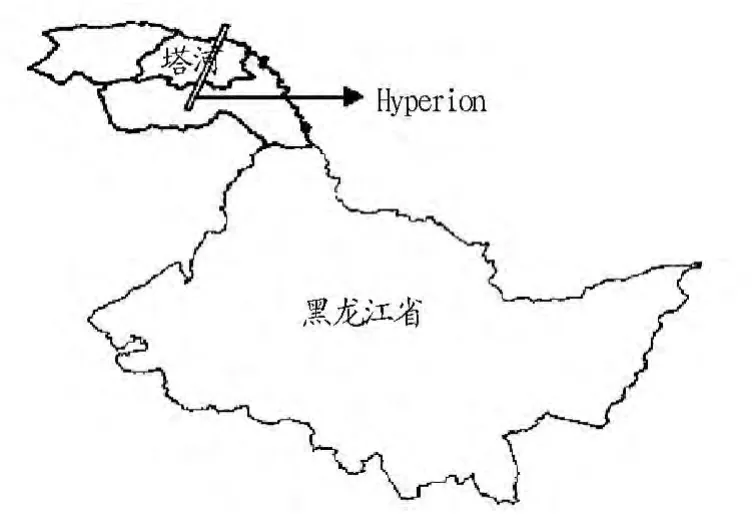
图1 塔河地区位置及Hyperion数据分布

2 数据及研究方法

2.1 遥感数据 Hyperion传感器是美国国家宇航局(NASA)于2000年11月21日发射的地球观测卫星(EO-1)上搭载的3个仪器之一，它提供了242个波段高光谱数据，平均光谱分辨率为10 nm，空间分辨率为30 m。该研究使用的是Hyperion Level 1R(L1R)级产品，L1R产品有242个波段，1～70为可见光近红外波段(VNIR)，71～242为短波红外波段(SWIR)，其中198个波段经过辐射定标处理，定标的波段分别为VNIR 8～57和SWIR 77～224由于VNIR 56～57与SWIR 77～78的重叠，实际上只有196个独立波段。

2.2 遥感数据处理 Hyperion L1级产品的预处理主要包括水汽吸收波段和非定标波段的剔除坏线的修复垂直条纹的去除、Smile效应的校正、大气校正、几何校正等。Hyperion数据存在Smile效应。该研究主要是应用MNF空间列均值调节法(Column Mean Adjusted in MNF Space)，通过对Hyperion图像进行MNF处理，得到最小噪声分离图像，观察变换结果，选择MNF变换后的前20个波段进行MNF逆变换，变换结果可以很好地去除Smile现象。由于高光谱图像受大气影响显著，为减少大气影响，降低噪声，提高图像数据质量，必须进行大气校正。该研究中采用FLAASH(fast line-ofsight atmospheric analysis of spectral hyper-cubes)模块［5-6］进行大气校正。FLAASH是基于MODTRAN-4的大气纠正模块，可以从高光谱遥感图像中复原地物的地表反射率。FLAASH模块结合了MODTRAN-4的大气辐射传输编码，任何有关图像的标准MODTRANMODTRAN大气模型和气溶胶类型都可以直接被选用，进行地表反射率的计算。FLAASH被广泛应用于高光谱和多光谱数据的大气校正［7］。该研究采用多项式校正方法，在Hyperion L1图像中采集16个控制点，运用二次多项式，对大气校正后图像进行几何校正。

2.3 研究方法 支持向量机(Support VectorMachines，SVM)是一种基于统计学习理论的机器学习算法，采用结构风险最小化(Structural Risk Minimization，SRM)准则，在最小化样本误差的同时缩小模型泛化误差的上界，从而提高模型的泛化能力。不同于一些机器学习算法通常采用经验风险最小化(Empirical Risk Minimization，ERM)准则，统计学习理论提出了一种新的策略:将函数集构造为一个函数子集序列，使各个子集按照VC维的大小排列;在每个子集中寻找较小经验风险，在子集间折衷考虑经验风险和置信范围，取得实际风险的最小化，这种思想称作结构风险最小化［8］。支持向量机的基本数学形式是:

约束条件:

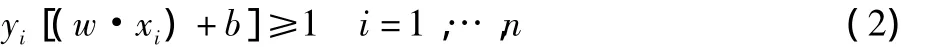
引入拉格朗日乘子ai上式求解方程为:

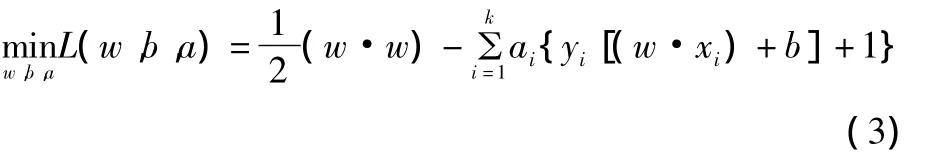
约束条件:

高粱整地工作主要是为了施肥而打基础，因此高粱种植人员需要做好前期准备。例如，耕地、除草等方法，以上操作环节主要是为了高粱种植提供良好的基础。具体方法需要结合各地区的实际情况而定，要遵循因地制宜的原则，具体根据种植地区的当期自然环境而定。

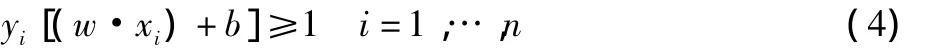
对w、b求偏导，得到:

将式(5)代入式(3)得到:

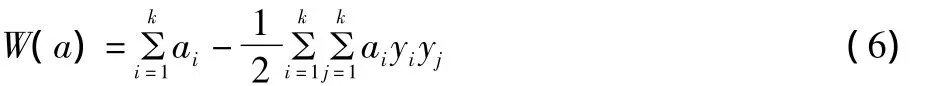
对于高维空间，如果用内积K(x;x')代替最优分类面积中的点积，就相当于把原特征空间变换到了某一新的特征空间，此时的优化函数为:

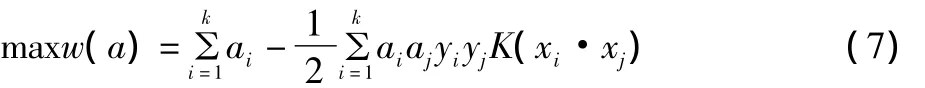
约束条件:

ai为与式(3)中每个样本对应的Lagrange乘子。这是一个不等式约束下二次函数寻优的问题，存在唯一解，而且解中将只有一部分(通常是少部分)ai不为0，对应的样本就是支持向量。

求解上述问题后得到的最优分类函数是:

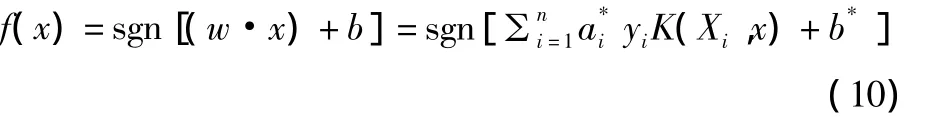
式中的求和实际上只对支持向量进行b*是分类阈值，可以用任一个支持向量求得，或通过两类中任一对支持向量取中值求得。其中核函数K(xi;x)可以有多种形式。

(1)线性核:

(2)多项式核:

式中，d是自然数。

(3)RBF核(Gaussian径向基核):

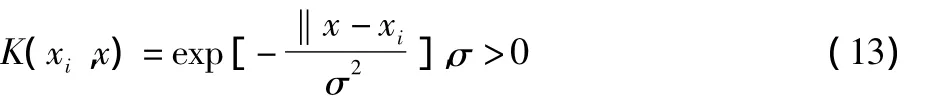
(4)Sigmoid核:

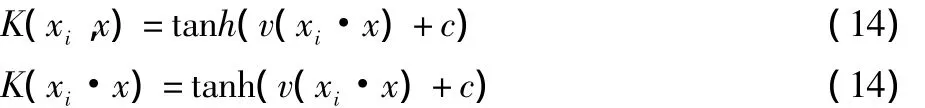
式中，S是Sigmoid函数;a、t是某些常数，一般根据不同分类体系进行确定。

SVM的实质在于:首先通过非线性变换将输入空间变换到一个高维空间，然后在这个高维空间中进行线性回归，求取最优线性分类面，而这种非线性变换是通过定义适当的内积函数实现的。

3 结果与分析

3.1 分类结果 该研究在155个波段中根据地物光谱特点选取具有代表性的21个波段进行分类;选取样本时充分地考虑了各种地物的光谱结构和纹理特征，在该研究中样本种类分别为河流、草地、水田、旱田、道路及建筑区、白桦为主的阔叶林、樟子松为主的针叶林、针阔混交林8种类型。不同的核函数对应不同的特征映射，从而所学习得到的SVM分类超平面也具有不同的特点和能力。核函数选择在SVM应用中非常重要，但到目前为止，还没有一个公认比较好的选择标准。为了比较不同核函数的识别效果，选择了SVM中的4种核函数(线性核、多项式核、径向基核、径向基核)对处理好的高光谱图像进行分类。分类结果如图2～5所示。

图2 线性核分类结果

图3 多项式核分类结果

图4 径向基核分类结果

图5 Sigmoid核分类结果

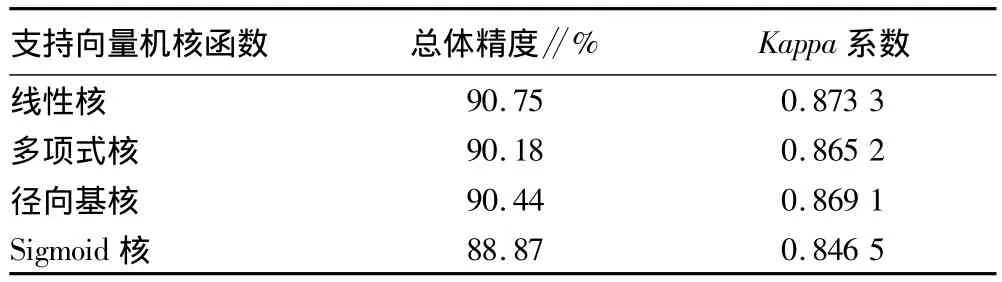
表1 不同核函数分类精度

3.2 精度验证 支持向量机分类方法中采用线性核、多项式核、径向基核、Sigmoid核不同的核函数的精度如表1所示。从表1可以看出，线性核函数分类精度最高，分类精度达到了90.75%，径向基核函数、多项式核函数、Sigmoid核函数精度依次降低，最低的分类精度是88.87%，但4种核函数的分类精度相差不是很大，最大与最小之间相差只有1.88个百分点。

该研究将研究区域的EO-1 Hyperion遥感图像划分为河流、草地、水田、旱田、道路及建筑区、白桦为主的阔叶林、樟子松为主的针叶林、针阔混交林8种类型。总体来看，对森林和水体的识别精度比较高，4种核函数的分类精度基本都超过了90%，4种核函数对农田、草地和道路及建筑区的分类精度不高，基本在80%左右。

表2 不同地物类别分类精度%

4 讨论

该研究采用基于支持向量机方法对大兴安岭塔河地区的EO-1 Hyperion遥感图像进行分类研究，并采用了不同的支持向量机分类核函数进行分类，对分类结果进行了精度对比，结果表明，4种核函数的分类精度相差不大，对于该研究线性核函数相对较好，分类精度达到了90.75%%，线性核、径向基核、Sigmoid核分类精度依次降低。但由于数据比较单一，环境局限，不能说明哪种核函数更适合什么地区，还需要继续进行相关研究才能掌握相关规律。

该研究只是对EO-1 Hyperion高光谱数据做了常规的预处理，并没有什么突破，在坏点、坏线和Smile现象处理中仍需要不断尝试新的方法，更好地恢复该数据。选取合适的纹理特征和其他形状领域等特征集成起来进行分类，有利于分类精度提高和速度提升。

［1］童庆禧.我国高光谱遥感的发展［N］.中国测绘报，2008-04-18.

［2］GOODENOUGH D G，DYK A，NIERNNN K O J，et al.Proeessing Hyperion and ALI for forest classification［J］.IEEE Transaetions on Geo-Science and Remote Sensing，2003，41(6):1321-1331.

［3］张辉.Hyperion高光谱数据条带噪声消除方法研究［J］厦门理工学院学报，2010，18(3):170-178.

［4］陈尔学，李增元，谭炳香，等.高光谱数据森林类型统计模式识别方法比较评价［J］.林业科学，2007，43(1):84-89.

［5］MATTHEW M W，ADLER-GOLDEN S M，BERK A，et al.Status of atmospheric correction using a MODTRAN4-based algorithm［J］.Proc SPIE，2000，4049:199-207.

［6］MATTHEW M W，ADLER-GOLDEN S M，BERK A，et al.Atmospheric correction of spectral imagery:Evaluation of the FLAASH algorithm with AVIRIS data［J］.Proc SPIE，2003，5093:474-482.

［7］ADLER-GOLDEN S M，ACHARYA P K，BERK A，et al.Remote bathymetry of the littoral zone from AVIRIS，LASH，and quickbird imagery［J］.IEEE Transactions on Geoscience and Remote Sensing，2005，43(2):337-347.

［8］张学工.关于统计学习理论与支持向量机［J］.自动化学报，2000，26(1):32-42.

［9］VAPNIK V N.Statistical learning theory［M］.New York:Wiley，1998.