高应变率下弹道明胶的本构模型研究
温垚珂,徐诚,陈爱军
(1.南京理工大学 机械工程学院,江苏 南京210094;2.南京理工大学 理学院,江苏 南京210094)
0 引言
弹道明胶被广泛应用于枪弹和破片终点效应的实验研究中。它是由明胶粉末和水按一定比例混合后经特殊工艺制成的一种物理响应类似肌肉的高分子材料[1]。弹道明胶按所含明胶质量百分比分为10%和20%两种类型,其中质量分数10%的明胶由于与肌肉的性质更相近,因此在国内外终点效应的研究中应用更广泛[2]。随着有限元技术的快速发展,数值计算方法开始应用于终点效应的研究与评判中。要进行合理正确的数值分析,首先要了解弹道明胶的物理特性并采用合适的本构模型来描述其物理响应。
Cronin 等[2-4]、Salisbury 等[5]采用自制的实验装置对质量分数10%弹道明胶(下文统称10%弹道明胶)从低应变率到高应变率(0.01 ~1 550 s-1)的应力应变响应进行了研究,实验表明弹道明胶是一种对应变率和温度较敏感的材料。Kwon 等[6]采用霍普金森压杆实验装置得到了10%弹道明胶在应变率2 000 ~3 200 s-1下的应力应变曲线,但其结果与Cronin 等[2-4]、Salisbury 等[5]的不一致。Parker等[7]研究了温度对10%弹道明胶物理性质的影响,实验表明当温度上升到30.5 ℃时明胶开始从凝胶转化为溶胶,而当温度降低到24.4 ℃时明胶开始从溶胶转化为凝胶。同时,还给出了明胶体积声速随温度的变化曲线。Nagayama 等[8]基于飞片实验得到了10%明胶的Hugoniot 曲线,实验表明弹道明胶质点速度与体积声速在一定压力范围内存在近似线性关系,同时还给出了弹道明胶密度随压力的变化曲线。Appleby-Thomas 等[9]采用飞片实验研究了质量分数25%的明胶、肥皂和猪油在高速冲击下的力学特性,研究表明随着应变率增加、25%的明胶呈现出流体弹塑性介质的性质,而肥皂和猪油则表现出明显的应变率增强效应。文献[10]采用布里渊光谱散射技术测量了不同压力状态(环境压力到12 GPa的压力)下弹道明胶体积声速和泊松比的变化情况。实验表明在一定压力下10%弹道明胶的泊松比大约为0.37,而一些研究者在数值模拟中经常将明胶考虑为类似橡胶的不可压缩材料(泊松比0.5)[3,11]。由于弹道明胶是一种高分子材料且较软,对其物理参数的实验测量技术还不够成熟,已公开发表的实验数据较少且存在不一致性,这给采用数值模拟技术进行终点效应研究带来一定困难。
现有的材料模型只能描述弹道明胶在某一特定应变率范围内的应力应变响应情况,根据研究问题不同,需要采用不同的本构模型。文献[12]建立了ABS 塑料球以低速(小于160 m/s)侵彻明胶的2D模型,该模型采用ALE 算法,将明胶考虑为简单弹性体,以拉伸极限应力作为明胶失效判断准则。针对手枪弹侵彻明胶的问题,Datoc[13]采用LS-DYNA中的弹塑性模型和粘弹性模型分别模拟弹道明胶,对明胶采用不同材料本构的数值结果进行了对比分析。文献[11]则采用LS-DYNA 中的不可压缩橡胶模型来模拟弹道明胶在软防护状态下的物理响应。Cronin[3]认为考虑应变率效应的超弹性模型可以较好模拟弹道明胶在准静态和中等应变率下的物理响应,但是文中没有给出该模型在高应变率下的验证结果。Minisi 等[14]开展了枪弹、球形破片侵彻明胶的数值研究工作,他们认为在高速侵彻下明胶可以看做流体,低速侵彻下明胶可以看做超弹性体,但是文献中没有给出具体的本构关系和材料参数。温垚珂等[15-16]采用流体弹塑性模型对钢球和步枪弹侵彻弹道明胶的过程进行了数值模拟,数值结果与实验结果一致性较好。目前,弹道明胶在高速冲击下的数值模拟问题还罕有文献报道,主要是缺少高应变率下准确的材料参数和合适的本构模型。
本文在综述弹道明胶物理性能的基础上,对用于模拟弹道明胶的两种不同本构模型(应变率相关的超弹性模型和流体弹塑性模型)进行了深入分析,并得到了10%弹道明胶的状态方程系数。基于球形杀伤元高速侵彻弹道明胶的实验研究,对比了两种不同材料模型所得数值结果与实验结果的一致性;认为在高应变率下流体弹塑性模型能更好地模拟破片与明胶的相互作用过程。
1 弹道明胶本构模型
1.1 应变率相关的超弹性模型
结合相关实验得知,弹道明胶具有较敏感的应变率效应,且在准静态和中等应变率下可以考虑为类似橡胶的不可压缩材料。而LS-DYNA 中的181 号材料模型(MAT_SIMPLIFIED_ RUBBER/FOAM)正是用以描述这类性质的较理想本构模型[17]。
该模型采用Ogden 应变能形式,即以主伸长率来表示应变能函数[18-20]:
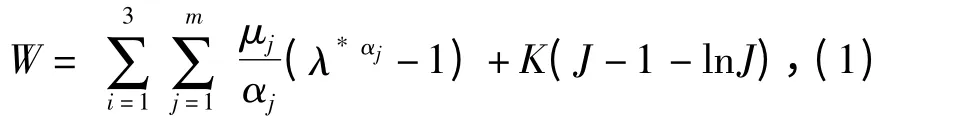
式中:μj和αj为材料常数;K 为体积模量;J 为压缩体积比;λ*i=λiJ-1/3,λi为主伸长率。由此得到主真实应力的表达式:
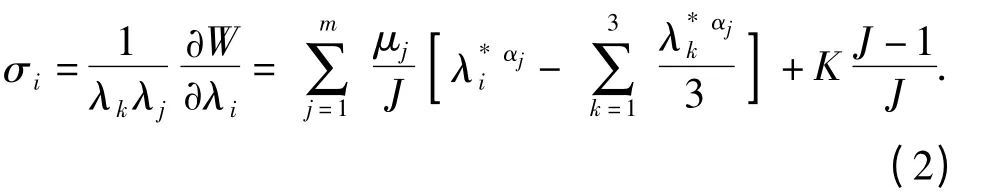
定义函数:
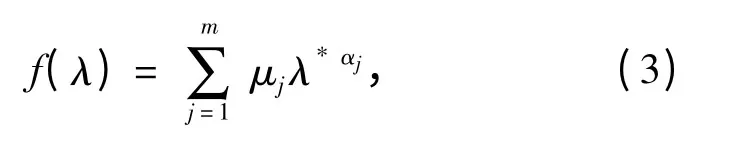
则主真实应力的表达式可以写成如下形式:
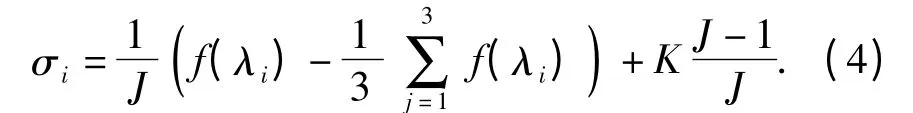
同时,该模型可以将不同应变率下的单轴测试拉压数据直接用于本构模型。采用线性插值的方法得到实验应变率范围内任意应变率下的应力应变响应[19-20]。图1为实验得到的10%弹道明胶在不同压缩应变率下的真实应力应变曲线[5]。由于明胶的拉伸实验技术还不够成熟,有关10%弹道明胶拉伸性质的文献未见公开报道,因此假设明胶在拉伸和压缩状态下具有相同的性质[3]。
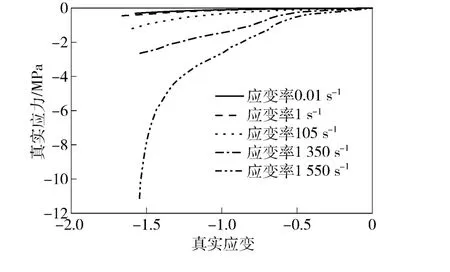
图1 10%弹道明胶在不同应变率下的真实应力应变曲线Fig.1 True stress-strain curves of 10% ballistic gelatin at different strain rates
基于Feng 和Hallquist[21]提出的失效准则如(5)式所示,该材料模型还可以模拟材料的失效过程。
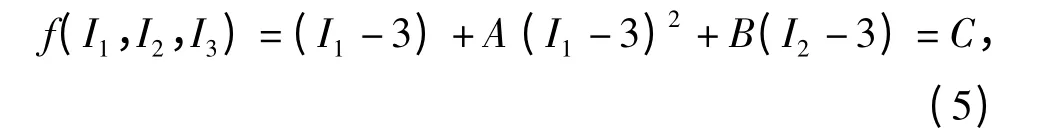
式中:I1、I2、I3为右Cauchy-Green 变形张量的3 个不变量,对于不可压缩材料I3=1;A、B、C 为由实验测得的材料常数。模型中通过损伤因子D 来考虑材料的应力衰减行为,D 的计算方法如(6)式所示。当D=1 时材料完全失效[17]。针对10%弹道明胶,Cronin[3]提出可以将(5)式简化为(7)式的形式,并基于实验数据得到C =5.7,h =0.2. (6)式中,h 用来判断材料何时开始失效。
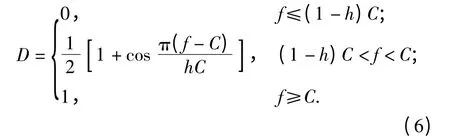
式中:
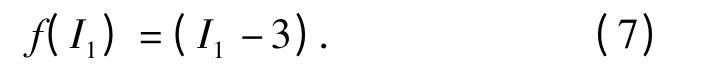
1.2 流体弹塑性模型
固体在动态较高压力下可以采用流体弹塑性模型来描述[17]。该模型不考虑应变率效应,但是结合状态方程可以考虑弹道明胶可压缩性的影响。流体弹塑性模型综合考虑了材料强度效应和可压缩效应,把变形视为形状变形和体积变形两部分之和。形状变形部分用小弹塑性本构方程描写,而体积变形部分用线性多项式状态方程描写[22-23]。
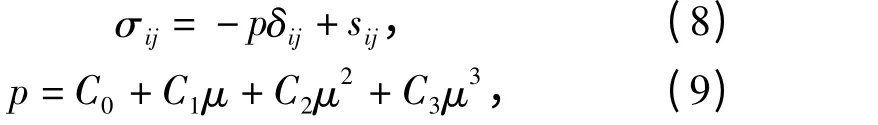
式中:σij为总应力张量;p 为静水压力;δij为单位张量;sij为应力偏张量;μ =ρ/ρ0-1,ρ 和ρ0分别为现时密度和初始密度;C0、C1、C2和C3为材料常数,需要经过实验测定和一定的理论推导才能得到。
Wilbeck[24]基于冲击波阵面上的质量、动量和能量守恒条件,推导出面后压力与密度存在如下关系:
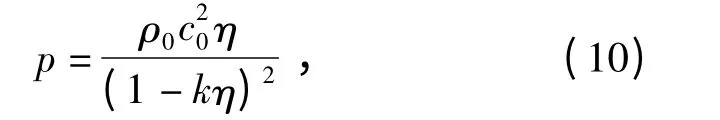
式中:η=1 -ρ0/ρ =μ/(1 +μ);c0为体积声速;k 为材料常速。c0和k 均需要通过实验测定。Nagayama等[8]通过实验得到了10%弹道明胶的Hugoniot 曲线,他们认为冲击波速us和质点速度vp之间存在如下线性关系:

式中:c0=1 520 m/s;k=2.
(10)式可以改写为如下的展开式:
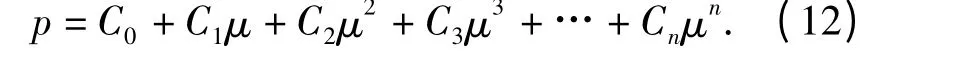
当μ 的范围不是很大的时候,(12)式一般采用(9)式的近似表达形式。其中C0在初始压力平衡时取0;C1=ρ0c20为体积模量;C2=(2k -1)C1;C3=(k-1)(3k-1)C1. 由此可以确定10%弹道明胶的状态方程系数如表1所示。

表1 10%弹道明胶状态方程系数Tab.1 The equation of state of ballistic gelatin
2 实验研究
实验数据可以检验数值方法的可行性与准确性,同时对实验现象观察及分析有助于建立正确合理的数值模型。本文采用弹道枪以不同初速(700 ~1 000 m/s)发射直径4.8 mm 的钢球射击10%弹道明胶(长× 宽× 高= 33 cm × 20 cm ×25 cm),弹道方向为明胶长度方向;光电靶测速系统记录钢球侵入明胶前的速度;高速摄影系统记录钢球在明胶中的运动过程及明胶中的空腔变化情况。如图2所示。
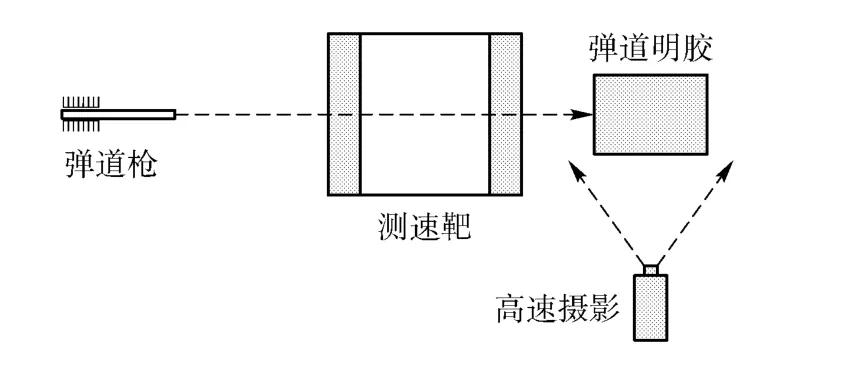
图2 实验装置示意图Fig.2 Schematic diagram of experimental setup
实验中观察到的主要现象为明胶中空腔的膨胀、收缩及脉动。观察实验后的钢球,发现无明显变形。因此可以考虑在数值模拟中采用刚体模型来模拟钢球,以提高运算速度。从表2中可以看到,两组入射速度下的实验结果一致性较好。该弹道明胶的弹道极限速度大约为730 m/s. 通过对高速摄影结果的后处理,还可以得到侵彻过程中钢球的速度衰减曲线及空腔膨胀周期等数据。
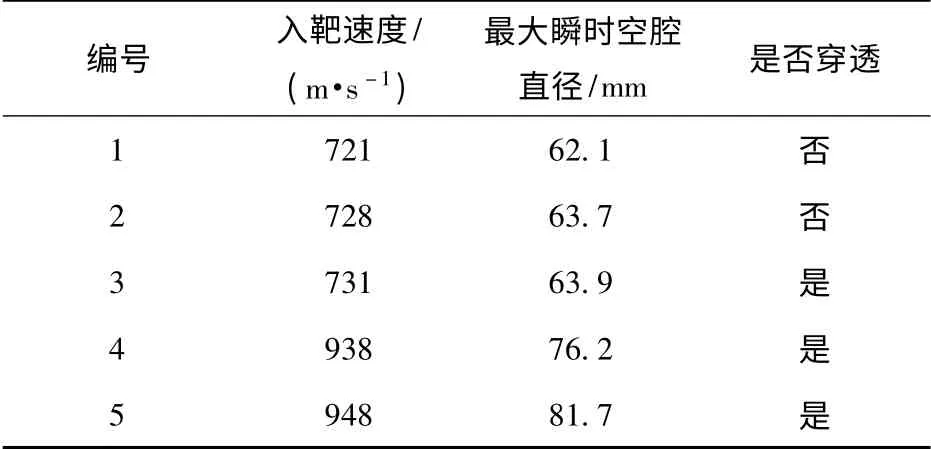
表2 φ4.8 mm 钢球以不同速度侵彻弹道明胶的实验结果Tab.2 Experimental results of φ4.8 mm steel sphere penetrating into ballistic gelatin at different velocities
3 数值结果与实验对比
3.1 有限元模型
建立与实验对应的有限元求解模型,考虑到对称性及求解效率,只需建立1/4 模型。数值模型采用Lagrange 算法,全部用Solid164 实体单元建立,在钢球与明胶之间采用面面侵蚀接触算法。进行网格划分时,如图3所示,钢球与明胶的直接接触区及附近划分较密的网格,远离弹道的区域网格尺寸逐渐增大。钢球采用刚体模型(MAT_RIGID),设定入射速度分别为721 m/s 和948 m/s. 明胶分别采用考虑应变率效应的超弹性本构和考虑可压缩性的流体弹塑性本构来模拟。
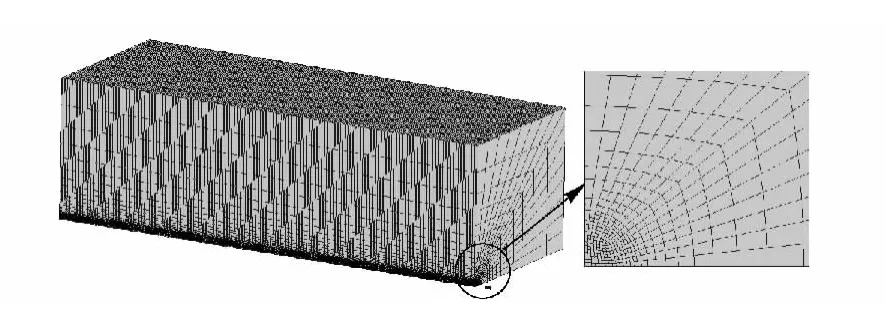
图3 钢球侵彻明胶的有限元模型Fig.3 The finite element model of steel sphere penetrating into ballistic gelatin
3.2 结果与讨论
从图4中可以看到,在两个速度段上流体弹塑性模型的结果均与实验结果较一致,而超弹性模型数值结果的误差较大。从图5中空腔形态的对比也可以明显看出,流体弹塑性模型的数值结果与实验比较接近,而考虑应变率的超弹性模型得到的瞬时空腔较小。在钢球侵入弹道明胶1 000 μs后,超弹性模型得到的瞬时空腔直径约为实验值的一半。
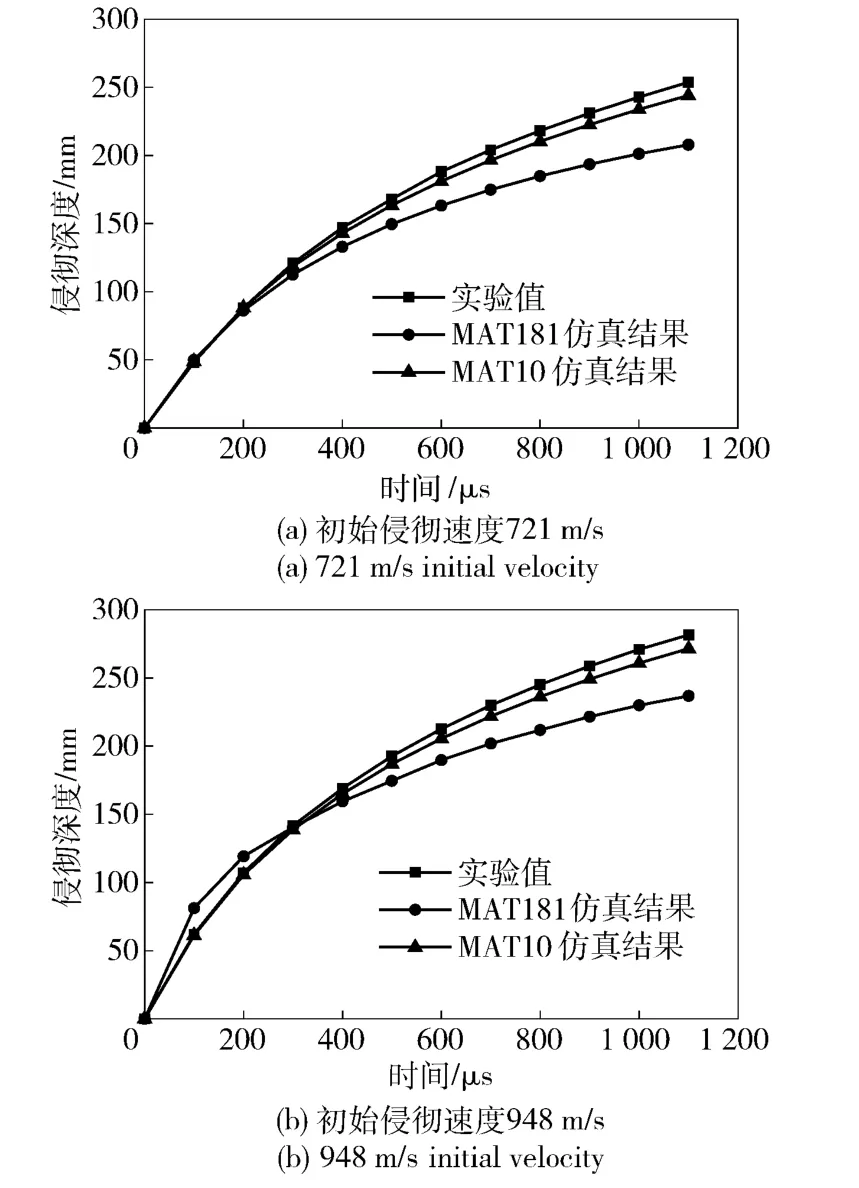
图4 两种材料模型计算得到的侵彻深度随时间变化与实验结果对比曲线Fig.4 Comparison of computed and experimental time histories of the penetration depths
从对比结果可以得到,在高速侵彻下考虑可压缩效应的流体弹塑性模型比考虑应变率效应的超弹性模型能更好地模拟弹道明胶的物理响应。这主要是由于弹道明胶在高应变率下的物理响应是由两个互相竞争的因素来决定的:1)由应变率增加导致的材料强化效应[3-4,6],2)由高压引起的材料可压缩效应[2,7-9,24]。当应变率增加时可压缩效应逐渐占优,当应变率降低时,应变率强化效应占优。因此明胶在准静态和中等应变率范围内可以采用应变率相关的超弹性模型来模拟,但是在高应变率范围内采用考虑可压缩效应的流体弹塑性本构能更准确地模拟其物理响应。

图5 钢球以721 m/s 的速度入射明胶时仿真得到瞬时空腔与高速摄影拍摄到瞬时空腔对比Fig.5 Comparison of computed and experimental temporary cavity profiles at a strike velocity of 721 m/s
4 结论
本文针对弹道明胶物理性质的实验研究情况及其在终点效应数值模拟中的应用,重点研究了可用于弹道明胶模拟的两种不同本构关系:应变率相关的超弹性本构和考虑可压缩性的流体弹塑性本构。结合相关实验数据推导得到了弹道明胶状态方程系数。随后进行了球形杀伤元高速侵彻弹道明胶的实验,并建立了对应的有限元模型。最后将采用两种不同本构模型得到的数值结果与实验数据进行了比较,得出流体弹塑性模型能更准确地模拟弹道明胶在高应变率下的物理响应结论。为采用数值方法研究枪弹及破片的终点效应提供了一定的借鉴。
References)
[1]Jussila J. Preparing ballistic gelatine—review and proposal for a standard method[J]. Forensic Science International,2004,141(2):91 -98.
[2]Cronin D S,Falzon C. Characterization of 10% ballistic gelatin to evaluate temperature,aging and strain rate effects[J]. Experimental Mechanics,2010,51(7):1197 -1206.
[3]Cronin D S. Ballistic gelatin characterization and constitutive modeling[M]∥Dynamic Behavior of Materials:Volume 1. New York:Springer,2011:51 -55.
[4]Cronin D S,Falzon C. Dynamic characterization and simulation of ballistic gelatin[C]∥SEM Conference and Exposition on Experimental and Applied Mechanics. New Mexico,US:Society for Experimental Mechanics,2009:1 -4.
[5]Salisbury C P,Cronin D S. Mechanical properties of ballistic gelatin at high deformation rates[J]. Experimental Mechanics,2009,49(6):829 -840.
[6]Kwon J,Subhash G. Compressive strain rate sensitivity of ballistic gelatin[J]. Journal of Biomechanics,2010,43(3):420 -425.
[7]Parker N G,Povey M J W. Ultrasonic study of the gelation of gelatin:phase diagram,hysteresis and kinetics[J]. Food Hydrocolloids,2012,26(1):99 -107.
[8]Nagayama K,Mori Y,Motegi Y,et al. Shock Hugoniot for biological materials[J]. Shock Waves,2006,15(3 -4):267 -275.
[9]Appleby-Thomas G J,Hazell P J,Wilgeroth J M,et al. On the dynamic behavior of three readily available soft tissue simulants[J]. Journal of Applied Physics,2011,109(8):1 -6.
[10]Aihaiti M,Hemley R J. Equation of state of ballistic gelatin(Ⅱ)[R]. US:Carinegie Institutioin of Washington DC Geophysical Lab,2011.
[11]Shen W,Niu Y,Bykanova L,et al. Characterizing the interaction among bullet,body armor,and human and surrogate targets[J]. Journal of Biomechanical Engineering,2010,132(12):121001.
[12]Koene L,Papy A. Experimental and numerical study of the impact of shperical projectiles on ballistic gelatin at velocities up to 160 m/s[C]∥25th International Symposium on Ballistics. Beijing,China:IBC,2010:1573 -1579.
[13]Datoc D. Fnite element analysis and modeling of a.38 lead round nose ballistic gelatin test[R]. San Luis Obispo,US:California Polytechnic State University,2010.
[14]Minisi M D. Gelatin Impact Modeling,PM-MAS ES-1A-9000[R]. [2013 -04 -10]. Http:∥dtic. mil/ndia/2006smarllarms/minisi.pdf.
[15]温垚珂,徐诚,陈爱军,等. 球形破片高速侵彻明胶靶标的数值模拟[J]. 弹道学报,2012,24(3):25 -30.WEN Yao-ke,XU Cheng,CHEN Ai-jun,et al. Numerical simulation ofspherical fargments penetrating into ballistic gelatin at high velocity[J]. Journal of Ballistics,2012,24(3):25 -30.(in Chinese)
[16]温垚珂,徐诚,陈爱军,等. 步枪弹侵彻明胶靶标的数值模拟[J]. 兵工学报,2013,34(1):14 -19.WEN Yao-ke,XU Cheng,CHEN Ai-jun,et al. Numerical simulation of the penetration of bullet on gelatin target[J]. Acta Armamentarii,2013,34(1):14 -19. (in Chinese)
[17]Hallquist J O. LS-DYNA keyword user's manual volume Ⅱ:material models[M]. CA,US:Livermore Software Technology Corporation,2012.
[18]Du-Bois P A. A simplified approach to the simulation of rubberlike materials under dynamic loading[C]∥4th European LSDYNA Users Conference. ULM,Germany:Livemore Software Technology Corporation,2003:31 -45.
[19]Kolling S,Du-Bois P A,Benson D J,et al. A tabulated formulation of hyperelasticity with rate effects and damage[J]. Computational Mechanics,2007,40(5):885 -899.
[20]Benson D J,Kolling S,Du-Bois P A. A simplified approach for strain-rate dependent hyperelastic materials with damage[C]∥9th International LS-DYNA Users Conference. Detroit,US:Livemore Software Technology Corporation,2006:29 -51.
[21]Feng W W,Hallquist J O. A failure criterion for polymers and soft biological materials[C]∥5th European LS-DYNA Users Conference. Birmingham,UK:Livemore Software Technology Corporation,2005:1 -10.
[22]吕洪生,曾新吾. 连续介质力学(下):动载固体力学与应力波[M]. 长沙:国防科技大学出版社,1999.LYU Hong-sheng,ZENG Xin-wu. Continuum mechanics:dynamical solid mechanics and stress waves[M]. Changsha:National University of Defense Technology Publish House,1999.(in Chinese)
[23]Johnson A F,Holzapfel M. Numerical prediction of damage in composite structures from soft body impacts[J]. Journal of Materials Science,2006,41(20):6622 -6630.
[24]Wilbeck J S. Impact behavior of low strength projectiles,AFMLTR-77-134[R]. US:Air Force Materials Laboratory,1978.

