基于样条函数表征目标运动轨迹事后数据融合方法研究

宫志华，周海银，郭文胜，徐旭

(1.中国白城兵器试验中心，吉林 白城137001;2.国防科学技术大学 理学院，湖南 长沙410073)

0 引言

针对常规武器系统发射目标机动性强、尺寸小、飞行高度低的特点，迫使测控系统向着一个多设备、多体制(光学、雷达、遥感)、多冗余的综合测控体系发展，也驱动着数据处理性能精准化程度要求日益提高。传统、独立、互不交融的数据处理方法不再满足数据处理要求，在此情形下，如何进行多冗余多结构异类测元数据综合处理，以获得更可靠的试验结果一直是学术界一个研究的热点。传统运动目标轨迹参数融合解算方法认为，运动目标在时序上不具有任何关联性，即在每一个采样时刻进行目标轨迹参数融合解算，这种方法没有充分利用测量数据之间的时序关联性[1]，使设计矩阵庞大，耗费运算资源，效率低。针对这一问题，本文结合机动、小型运动目标特点，提出采用基于自由节点样条函数来描述目标运动轨迹并转换，实现以其为基函数对测控设备测元进行表征，将冗余多源异类测元数据、多采样时刻的测量方程联合求解目标轨迹参数的融合方法。该方法充分考虑运动目标全程轨迹特征点和时序关联性，极大减小由数学模型表征目标轨迹造成的截断误差，大量压缩待估参数数量，提高目标轨迹参数估计精度和计算稳定度，同时对各测元潜在的系统误差进行多循环探查和估计，实现系统误差自校准的目的。

1 数据融合模型

1.1 联合误差方程建立与解算

考虑不同测控设备测量原理，可以提供的独立测元种类有多种，这里只列举常用的3 种:GPS、GLONASS、北斗空间定位测元(局部坐标(x，z，y)，由原始大地坐标(纬度b，经度l，大地高h)转换得到)、光学设备测元(方位角α，俯仰角θ)、脉冲雷达测元(距离r，方位角α，俯仰角θ)和连续波雷达测元(距离r，方位角α，俯仰角θ，径向速度v).下面，就以靶场常见的7 种独立测元(x，z，y，r，α，θ，v)为例，具体分析基于样条函数表征测元的联合误差方程的建立和解算过程。

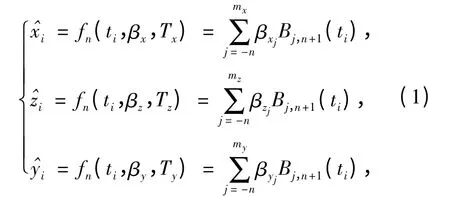
对(1)式进行一阶微分，可得到(2)式，

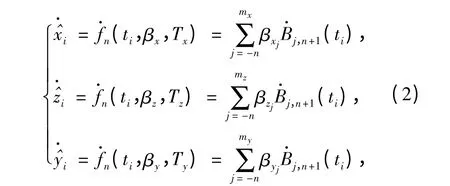
关于各测元误差方程的建立，除定位测元(x，z，y)外，其他测元(r，α，θ，v)均为非线性方程，需按泰勒级数展开转化为线性方程。则以(1)式、(2)式为基函数表征各测元误差方程公式推导总结如下:

定位测元误差方程

距离测元误差方程

方位角测元误差方程

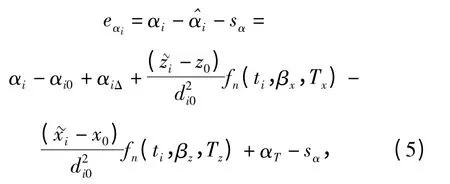
式中:αT为判象限角。俯仰角测元误差方程

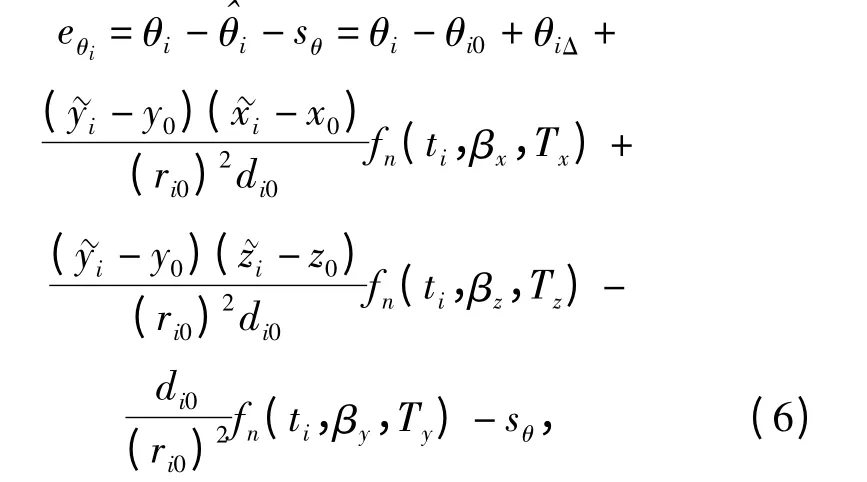
径向速度测元误差方程

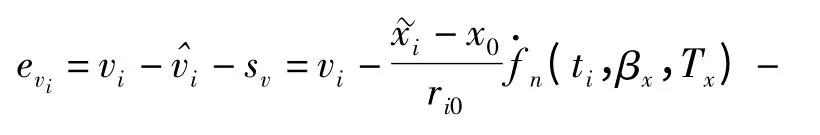
(3)式～(7)式中:(xi，zi，yi，ri，αi，θi，vi)为各测元实测数据;(sx，sz，sy，sr，sα，sθ，sv)为各测元系统误差模型，如常值、线性或非线性函数模型等;(初 值;(x0，z0，y0)为 站 址 已 知 坐 标;ri0=

将(3)式～(7)式各测元误差方程联立，组成目标轨迹联合误差方程，写成矩阵形式，如(8)式所示。

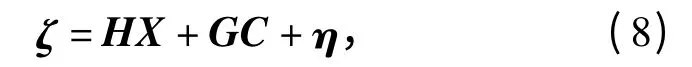
式中:ζ=(exi，ezi，eyi，eri，eαi，eθi，evi)T为测元残差向量;H 为与样条函数有关的系数矩阵(亦称为设计矩阵);X = (βx1，…，βx(mx+n+1)，βz1，…，βz(mz+n+1)，βy1，…，βy(my+n+1))T为与样条函数有关的待估参数向量;G 为系统误差模型系数矩阵;C 为系统误差模型待估参数向量;η=(xi，zi，yi，ri－ri0+riΔ，αi－αi0+αiΔ，θi－θi0+θiΔ，vi)T为常数向量。

在参数估计时，在大数据量处理的情况下，相关性和非高斯性对估计结果影响不大[3]，因此采用白噪声条件下的参数估计方法，在已知最优节点分布的前提下，由最小二乘法原理解算可以得到待估参数(样条拟合函数系数和系统误差模型系数)和其协方差矩阵解，如(9)式所示，

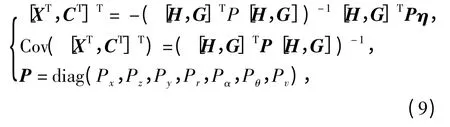
式中:P 为权值矩阵。在实际求解中，由于初始目标轨迹参数的近似性和非线性函数级数展开带来的截断误差，需要进行叠代计算。将最终解算得到的样条函数拟合系数和系统误差函数系数代入目标轨迹参数表达式和误差函数表达式中，即可得到融合计算后的目标轨迹坐标值和系统误差值。

1.2 轨迹误差理论分析

现在考虑融合后目标轨迹坐标的精度估算问题。首先，测元值可写成(10)式的矩阵形式，

即测元值Y 是由以样条拟合系数β 和系统误差模型系数φ 为参数的F 函数表征，ξ 为测元残差向量。这样，将函数F 在样条系数估值处展开[4]，则近似地有

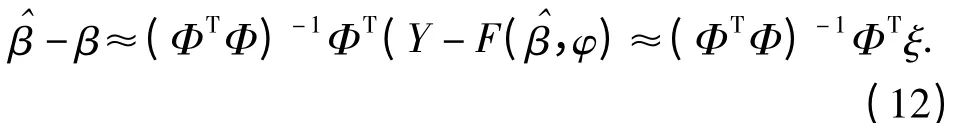
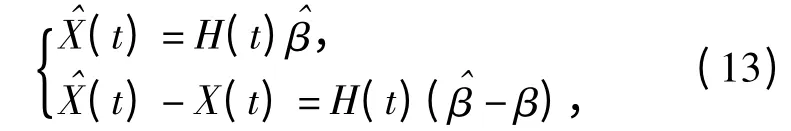
式中:H(t)=(Bx(t)T，Bz(t)T，By(t)T)T为样条基系数矩阵;X(t)为目标轨迹坐标的真值。目标轨迹坐标协方差为

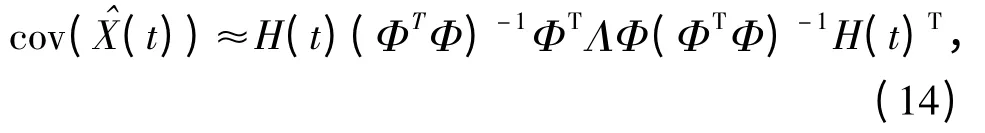
式中:Λ 为由测元残差ξ 的方差组成的对角阵。

1.3 样条节点优化拟合

以上采用样条函数表征目标轨迹，为减小截断误差，必须优选样条节点分布。关于样条节点的选取，首先的一个想法是可以采用等距节点。等距节点的实质是相当于采用一个恒定频率带宽的滤波器对数据进行滤波，但是由于非平稳数据所含噪声频率成分较多，且存在特征点现象，显然，采用恒定滤波器对数据滤波，要达到更好的精度，必然要使用更密的节点数以减小滤波器带宽，这对于节省待估参数进行融合解算是不利的[5]，因此，针对机动、非平稳目标轨迹特性，必须采用自由节点样条函数来对其表征，并在一定约束条件下对节点分布进行优化搜索。

如(1)式所示，用样条函数表征目标轨迹，以x方向为例，可以表示成矩阵形式，如(15)式，

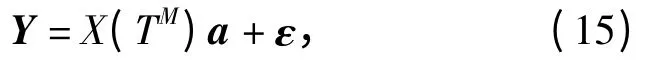
式中:a= (a0，a1，a2，…，amx)T为样条系数参数向量;Y=(x1，x2，…，xn)T为目标轨迹向量;ε =(ε1，ε2，…，εn)T为随机误差向量。

上式参数估计可归为如下非线性优化问题:即求样条拟合系数a 和节点分布TM(M 为节点个数)，使得

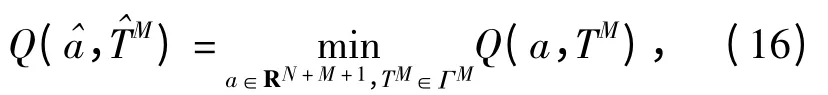
式中:Q(a，TM)=‖Y －X(TM)a‖2=(Y －X(TM)·a)T(Y－X(TM)a).

为定量给出低频信号与随机误差的分频界限，定义一个BIC 值进行判断[2]，如(17)式所示，

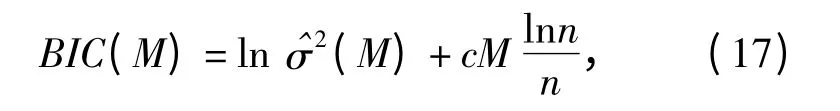
对于(16)式的多参数非线性目标函数，可以采用多种优化算法，文献[5]对这些算法的原理和实现都有详细的说明。本文采用的是模拟退火法。

需要特别注意的是，特征点必须作为已知样条节点使用，参与搜索其他最优节点，以避免产生较大的截断误差。特征点的获得可以采用遥测信息、光学图像判读、雷达回波谱分析和目标轨迹加速度曲线[7]分析等多种手段。

图1 目标轨迹三维坐标样条函数拟合BIC 值曲线Fig.1 The BIC values of three－dimensional trajectory based on spline function representation

2 应用与分析

对以上数据融合方法的合理性、正确性和实用性进行验证分析，结合某靶机飞行试验展开，分别有光学、雷达、遥感等测控设备参试跟踪靶机，包括红外光学经纬仪、脉冲雷达和连续波雷达，其中遥测设备记录GPS 机载设备星历原始数据，事后提供经过GPS 载波相位差分修正后的高精度靶机轨迹坐标数据作为比对真值数据，定位精度优于0.5 m.

选取8 个独立原始测元参与靶机轨迹融合计算，包括红外光学经纬仪两站测量的4 个独立测元数据(方位角和俯仰角)、脉冲雷达测量的3 个独立测元数据(距离、方位角和俯仰角)和连续波雷达测量的1 个独立测元数据(径向速度)。各测元原始数据采样频率不一致。

结合以上联合误差方程建立和最优节点搜索方法进行靶机飞行轨迹数据融合计算。

首先，对8 个独立测元实测数据分别进行已知系统误差修正、跨零跳点修正、合理性检验、数据插值和数据平滑等预处理项工作，本方法不需要进行地球曲率修正。其中，最后比较重要的一项内容是对各测元实测数据进行随机误差统计，可参考文献[6]相关方法。在数据融合处理中，各测元权重是不一样的，随机误差小表示精度高，权值相对大;反之，权值相对小。因此，以独立测元等方差和各测元不相关为依据，由各测元统计方差组成权值系数对角矩阵。

其次，对样条函数最优节点进行搜索确定，选取目标轨迹初值，可以为光学交会数据、雷达定位数据或理论轨迹数据等。考虑本实例中目标轨迹变化比较平稳，因此，先以脉冲雷达定位数据为初值，采用等距节点进行联合方程的解算，测元系统误差不考虑，再用融合后的目标轨迹数据进行最优节点的搜索。其中，公共段数据采用预处理后的50 ～100 s数据，数据采样频率为10 Hz，则按5 s 等间隔取内节点数量为9 个。

然后，分别对初次融合后获得的目标轨迹进行三次B 样条函数拟合，按以上方法搜索样条函数最优节点分布，得到目标轨迹三维坐标样条函数拟合效果的BIC 判定值，如图1 所示。

从图1 可以判断目标轨迹在三维方向上由样条函数拟合的最优节点数不是9 个，而是10 个，接着将搜索获得的最优节点分布分别代入(1)式，并依据以上建立的联合误差方程求解待估参数。

关于各测元系统误差模型的确定，在实际解算过程中可以采用以下过程:1)通过理论分析、比对等手段可以先确定一些测元系统误差的先验信息;2)无先验信息情况下，在初次融合解算时，先不考虑系统误差，查看融合解算后的各测元残差曲线特征;3)对残差有明显趋势项的测元，依残差趋势项特征建模，并重新融合解算，再查看各测元残差曲线特征，循环往复，直到所有残差均值为0;4)各测元系统误差模型需尽量简单。依据的原则是，如果各测元不存在系统误差或系统误差建模正确，则融合后各测元对应的残差应没有明显的趋势项，接近纯随机误差[5]。

本实例在无误差融合解算后发现多数测元残差曲线的均值不为0，如图2 所示，统计结果如表1 所示，表1 中α1、θ1为1 号经纬仪测元，α2、θ2为2 号经纬仪测元，α3、θ3、r3为脉冲雷达测元，v 为连续波雷达测元。这表明参与数据融合的8 个独立测元中，某些测元必定含有系统误差，并感染到了其他测元。

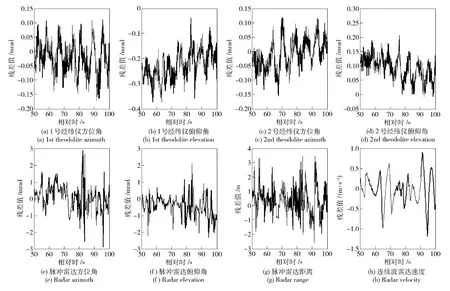
图2 不考虑系统误差情况下融合解算后各测元残差曲线Fig.2 The residual of each measuring element based on data fusion without system error

表1 不考虑系统误差融合解算后各测元残差统计值Tab.1 The residual statistic of each measuring element based on data fusion without system error

经过不断地对各测元系统误差模型的假设建立，并查看融合计算后残差曲线的均值情况，最后判定两站光学经纬仪的俯仰角测元和脉冲雷达的3 个测元均含有常值系统误差。这样，在最终联合方程中需要求解的待估参数总数量是47 个，其中，样条函数待估系数参数是42 个，系统误差待估参数是5 个。经过最后的融合解算，得到各测元残差曲线，如图3 和表2 所示。从表2 中可以明显看到，各测元残差均值都为0;测元的系统误差值也被探查出来，可用于修正原始测元数据。目标轨迹坐标的理论误差估计值如图4 所示，统计结果如表3 所示。

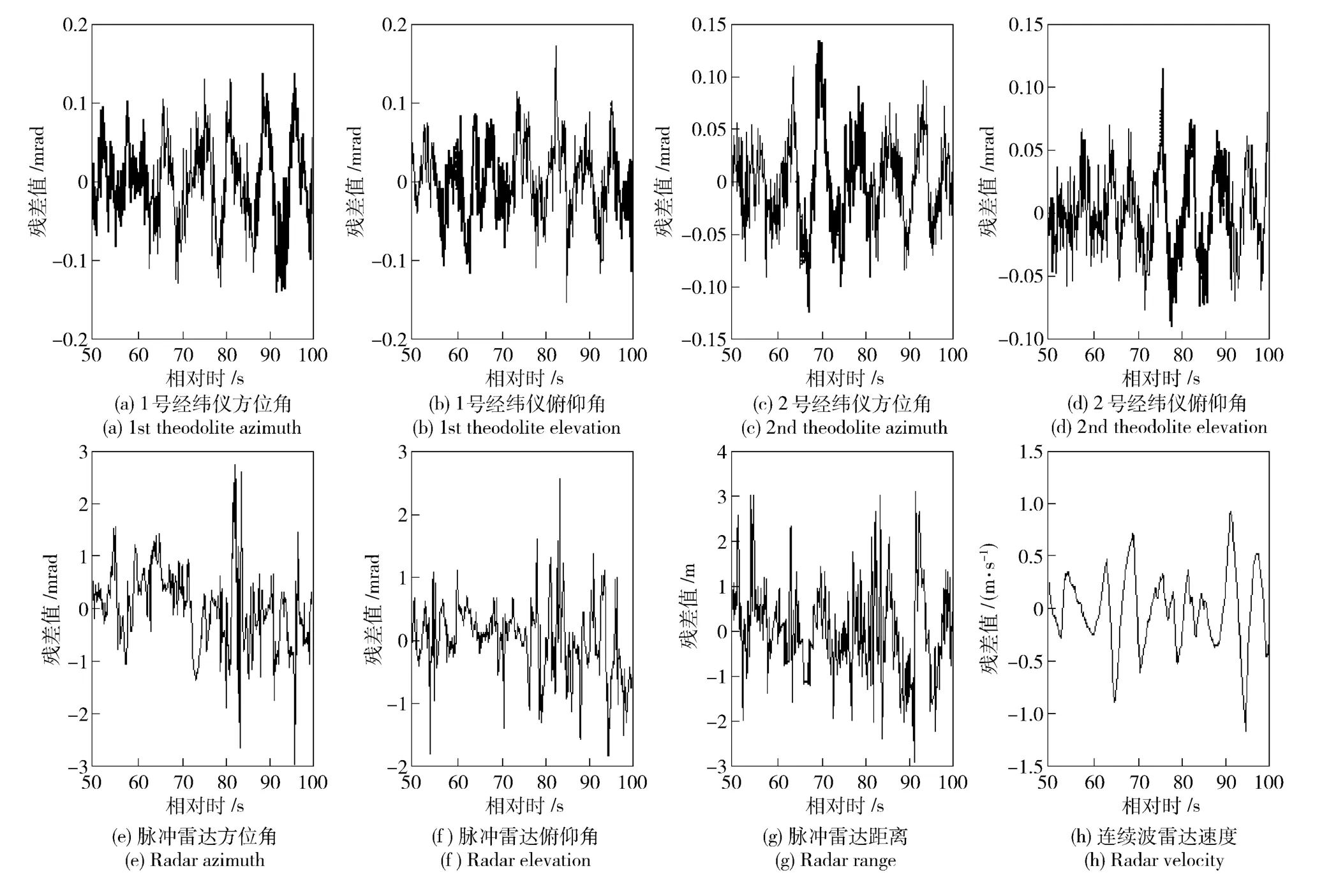
图3 考虑系统误差情况下融合解算后的各测元残差曲线Fig.3 The residual of each measuring element based on data fusion with system error

表2 考虑系统误差融合解算后各测元残差统计值Tab.2 The residual statistic of each measuring element based on data fusion with system error

表3 融合目标轨迹理论误差统计结果Tab.3 The theoretical error statistic based on data fusion

下面，为能直观地表现融合数据的质量和效果，以GPS 定位数据为真值，与两站光学经纬仪交会的目标轨迹坐标数据和由数据融合得到的目标轨迹坐标数据进行比对，查看两组比对误差，如图5 和图6所示，统计结果如表4 所示。

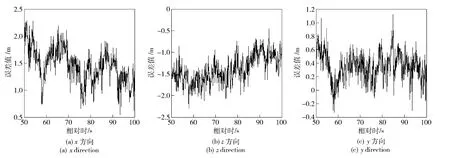
图5 光学交会目标轨迹数据与GPS 定位数据比对误差曲线Fig.5 The error comparison between optical－theodolite and GPS data

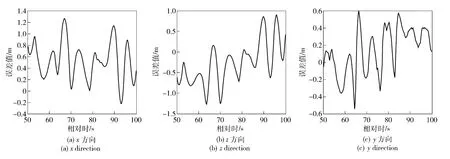
图6 数据融合目标轨迹数据与GPS 定位数据比对误差曲线Fig.6 The error comparison between fused trajectory data and GPS data

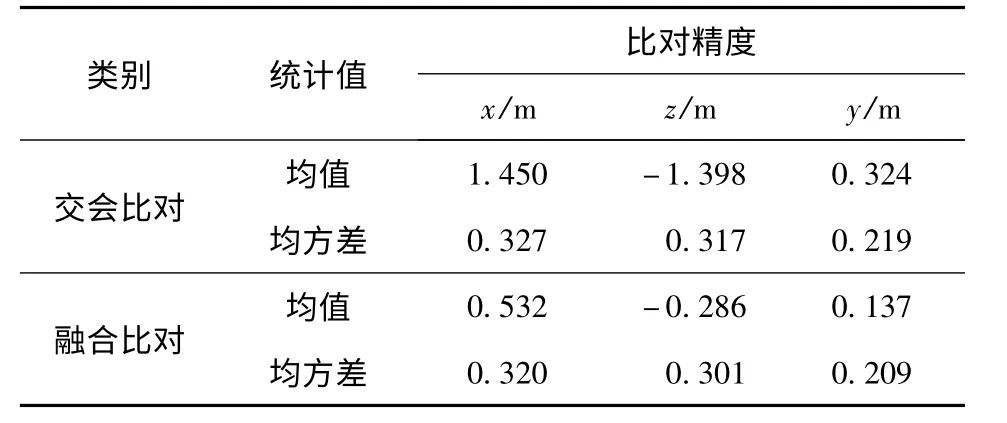
表4 两种目标轨迹与GPS 数据的比对残差统计结果Tab.4 The residual statistic comparison of two larget trajectories with GPS data

从表4 比对误差统计结果来看:1)数据融合比光学经纬仪交会的目标轨迹坐标数据方差和均值都小，更接近真值;2)两组比对误差均值都不为0，因为都含有跟踪部位不一致和大气折射误差修正残差所带来的误差，但光学交会数据还存在由测元系统误差造成的交会误差。

3 结论

基于以上分析，可以得到如下结论:

1)结合运动目标轨迹时序关联特性，可以实现以样条函数为基函数对测控设备各种测元进行表征;结合目标运动特征点情况和建立合理目标函数对样条函数最优节点进行优化搜索解算，使节点分布自适应目标运动特性，极大减小截断误差。这两种手段使得联合误差方程的待估参数被极大压缩，冗余程度极大增强，计算稳定性和效率也提高。

2)建立基于样条函数表征目标轨迹的稀疏参数联合误差方程，在实际计算过程中，对初值准确度要求不高，迭代计算收敛快，解算精度高，这对于需要多次循环反复进行的融合处理过程将极大地提高处理效率，并对各测元潜在系统误差具有较敏感的探查能力。因此，该方法实际应用效果明显。

3)上述针对运动目标轨迹数据融合计算方法得到的结果不是最优。因为，由于样条函数最优节点和权值都需要在融合前确定，由目标轨迹初值或半程融合得到的目标轨迹来约束搜索获得的节点分布不是最优;由高斯—马尔可夫定理又知，线性方程融合最优权值可由统计方差获得，但非线性方程并不是最优[7]。

关于目标运动轨迹数据融合研究领域，当前，有专家学者提出在融合模型中将节点和权值都当作待估参数，通过融合模型迭代计算改进节点和权值估计[8]，这种方法由于解空间维数高，计算量大、非线性程度高和效率低等问题，其工程实用性还有待进一步完善。因此，这一领域的工程研究今后还会不断深入地进行下去。

References)

[1]朱武宣，高耀文.基于样条约束“EMBET”的再入轨道测量数据融合方法[J].飞行器测控学报，2005，24(6):49 －53.ZHU Wu－xuan，GAO Yao－wen.A data fusion method for re－entry ballistic measurementwith spline restraint EMBET[J].Journal of Spacecraft TT＆C Technology，2005，24(6):49 － 53.(in Chinese)

[2]王正明，易东云，周海银.弹道跟踪数据的校准与评估[M].长沙:国防科技大学出版社，1999.WANG Zheng－ming，YI Dong－yun，ZHOU Hai－yin.Tracking trajectory data calibrating and evaluating[M].Changsha:National University of Defense Technology Publishing House，1999.(in Chinese)

[3]原野.基于GNSS 和陆基测量的外弹道数据事后融合方法研究[D].长沙:国防科学技术大学，2008.YUAN Ye.Research on the post－flight method of exterior ballistic measurement with GNSS data and ground－based TT ＆C network data[D].Changsha:National University of Defense Technology，2008.(in Chinese)

[4]童丽，易东云.非线性融合模型的弹道估计精度评定[J].弹道学报，2002，14(4):1 －5.TONG Li，YI Dong－yun.Assess accuracy of orbit parameters estimated from nonlinear fusion model[J].Journal of Ballistics，2002，14(4):1 －5.(in Chinese)

[5]宫志华，董立涛，徐旭.外弹道测量数据融合方法研究[J].兵器试验，2012，261(3):1 －6.GONG Zhi－hua，DONG Li－tao，XU Xu.The method of exterior measured trajectory data fusion[J].Ordance Test，2012，261(3):1 －6.(in Chinese)

[6]王正林，龚纯，何倩.精通MATLAB 科学计算[M].北京:电子工业出版社，2007.WANG Zheng－lin，GONG Chun，HE Qian.Master matlab scientitic calculation[M].Beijing:Publishing House of Electronics Industry，2007.(in Chinese)

[7]朱炬波.不完全测量数据建模与应用[D].长沙:国防科学技术大学，2004.ZHU Ju－bo.The incompletely measured data modeling and appling[D].Changsha:National University of Defense Technology，2004.(in Chinese)

[8]周海银.空际目标跟踪数据的融合理论和模型研究及应用[D].长沙:国防科学技术大学，2004.ZHOU Hai－yin.Researches on theories and models of spatial targets tracking data fusion with applications[D].Changsha:National University of Defense Technology，2004.(in Chinese)