硬质合金刀具的动态可靠性灵敏度研究
王新刚,李鹤,吕春梅,王雪玲,逄旭
(1.东北大学 控制工程学院,河北 秦皇岛066004;2.东北大学 机械工程与自动化学院,辽宁 沈阳110819)
0 引言
在当今机械制造及切削加工自动化系统不断提高的同时,对刀具可靠性的要求也越来越高。刀具可靠性差,会产生废品,损坏机床和设备,甚至造成人员伤亡。硬质合金刀具具有较高的耐热性和耐磨性,切削性能优良等特点,广泛应用于断续切削淬硬钢。从以往的实验数据看,其主要的失效形式是疲劳破坏[1-2]。目前,国内外学者对于切削速度、切削用量和刀具几何参数等因素对刀具寿命及可靠性的影响研究较多,且有大量的实验数据来说明上述参数的敏感度[3],而对硬质合金刀具的物理参数和材料参数的可靠性灵敏度研究以及考虑冲击载荷作用次数的灵敏度计算方法还未有报道。
本文从可靠性的概念出发,结合随机过程、应力-强度干涉(SSI)模型、灵敏度等数学力学方法,建立硬质合金刀具的动态可靠性及灵敏度的数学模型。研究刀具物理参数和材料参数的可靠性灵敏度变化规律,为进一步完善硬质合金刀具可靠性和可靠性灵敏度奠定理论基础。同时设计人员可以迅速找到敏感参数并加以控制来保证刀具的高可靠性[4-6],省去了大量的物理实验,节约成本。
1 硬质合金刀具的动态可靠性模型建立
目前数控机床使用的硬质合金刀具构成材料大部分为粉末冶金,其内部组织不均匀性使得刀具产品内部存在着许多微观裂纹。刀具在切削工件时受到随机变化的切削力作用,致使刀具内的裂纹核发生疲劳扩展,最后导致刀具发生疲劳破坏。还有一小部分刀具产品中的裂纹核初始尺寸几乎接近其临界断裂尺寸,当切削工件时就容易发生崩刀,出现早期失效[7]。
为了降低刀具的失效概率,需要对刀具可靠性敏感的参数进行分析研究,建立刀具可靠性和灵敏度分析的数学模型。本文提出了以SSI 模型为基础的刀具内部应力与临界疲劳应力干涉的数学模型作为刀具的失效判据,即以应力极限状态表示的状态方程为

式中:σ 为刀具体内某一点应力;σt为刀具临界疲劳应力;X 为随机变量向量。
刀头内的应力分布F(σ)函数通过现有的实验数据和有限元分析是很容易确定的,如果知道了刀具材料的临界疲劳应力σt的分布函数Ft(σ)以及其概率密度函数ft(σ),利用可靠性理论中的干涉理论,就可以确定刀具的可靠度,即
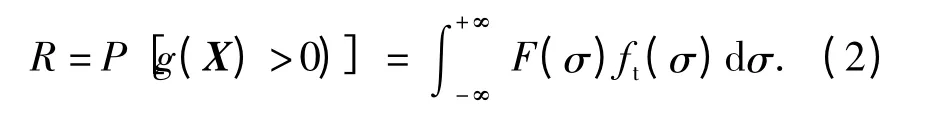
硬质合金刀具在断续切削工件时,失效的主要原因是由于其内部微观裂纹受到冲击载荷作用而发生疲劳扩展,当刀具内部应力没有达到刀具临界疲劳应力时,刀具不一定马上失稳扩展,而是要冲击N 次才能失效,所以考虑冲击载荷作用次数的等效载荷的累积分布函数[8-10]为
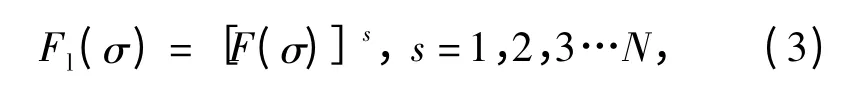
其概率密度函数应为
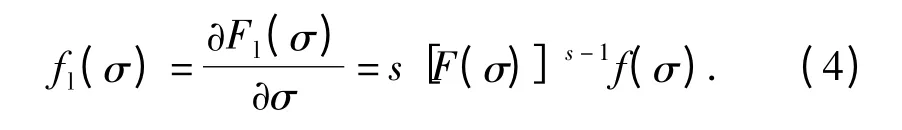
所以,考虑冲击载荷作用s 次的SSI 模型可靠度计算公式应为
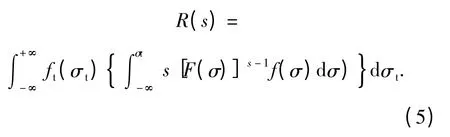
当s=1 时,(5)式变为传统的SSI 模型。
由于冲击载荷作用次数是随着加工时间的增加而递增的,所以冲击载荷作用过程可用泊松随机过程来描述[11]。当冲击载荷作用次数N(t)服从参数为λ(t)的泊松随机过程时,在任意时刻t 冲击载荷出现s 次的概率可表示为
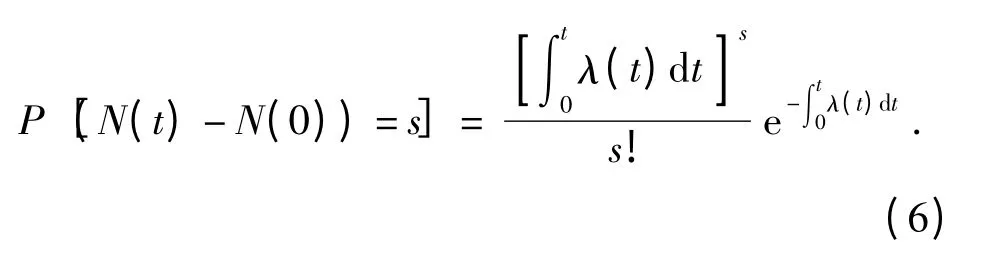
由(5)式、(6)式可知,刀具在t 时刻的可靠度为
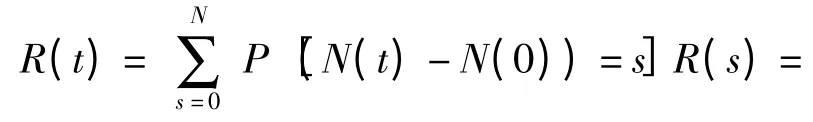
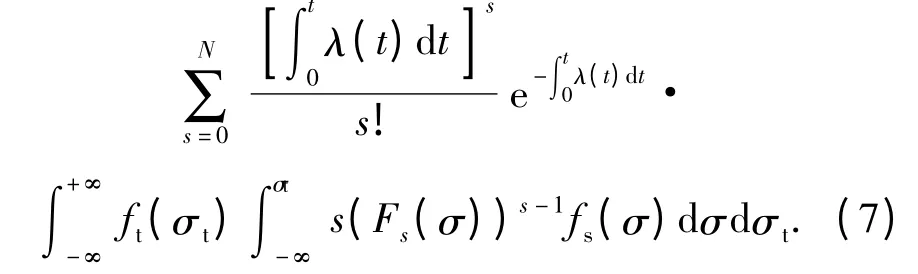
由(7)式可知,只要确定了临界疲劳应力σt的概率密度函数ft(σ),就可以求出刀具的动态可靠度。一般刀具材料的抗弯强度比较容易测出,根据抗弯强度和抗拉强度之间的关系,可以确定出抗拉强度的分布,然后根据裂纹的疲劳扩展过程,把抗拉强度和临界疲劳应力进行等效,即可求出临界疲劳应力的分布。
硬质合金刀具在机械冲击和热冲击的双重作用下,刀片内的裂纹核发生疲劳扩展,最后导致刀具发生破损,其中机械冲击应力主要与切削速度和进给量有关,热冲击应力主要与切削速度有关。而刀具发生早期破损时热应力影响很小,主要是机械冲击造成的。当刀具内部微观裂纹受到冲击作用时发生疲劳扩展[12],使其裂纹尖端应力强度因子达到或超过其材料的断裂韧性而发生断裂。当刀具内存在一定长度的裂纹时,施加于其上的应力不同,断裂时的裂纹长度也必定不同。假设刀片内最危险处存在一长度为lei的裂纹,当对其施加σc力时,裂纹马上断裂,即不发生疲劳扩展,这时必定有

式中:lei、lc为裂纹长度;KIC为平面断裂韧性;Y 为裂纹形状因子;σc为应力;
而对于同一长度的裂纹,施加另一应力σt(σt<σc)时,裂纹不一定马上失稳扩展,而是可能要冲击N 次才能失效,即

式中:l 为裂纹长度;N 为刀具寿命;n、A 为材料参数,可由Ⅰ型裂纹扩展速率测得;ΔKI=KImax- KImin为等效应力强度因子幅值,当切削力在0 ~Fmax之间变化时,有
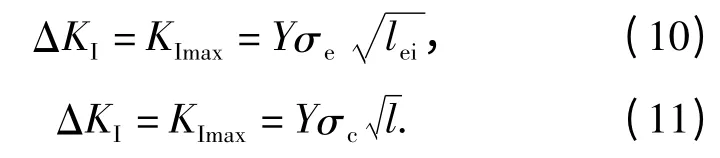
对(9)式积分得
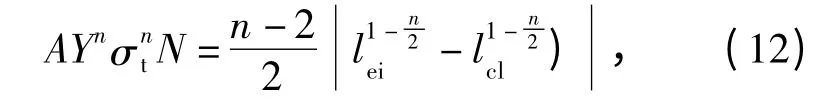
式中:lcl为施加σt时裂纹的断裂长度。当lcl≫lei时,则有
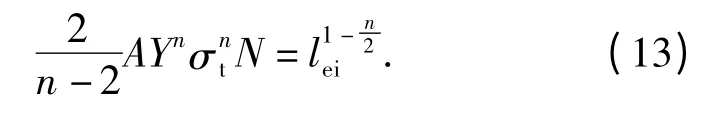
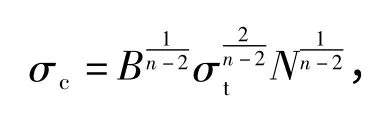
式中:
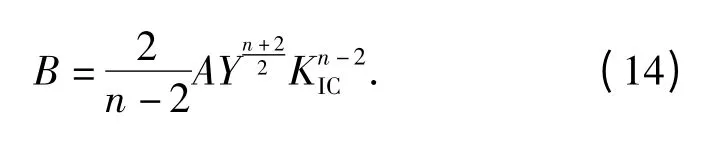
由文献[13]可知材料的抗拉强度服从威布尔分布,所以其概率密度函数为
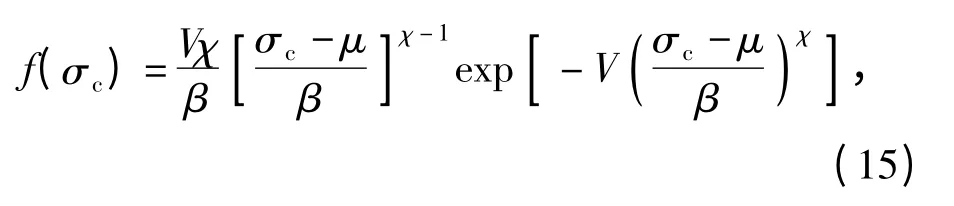
式中:V 为试件体积;χ、β、μ 分别为抗拉强度的形状参数、比例参数和位置参数;
结合(14)式和(15)式,可得临界疲劳应力的概率密度函数,即
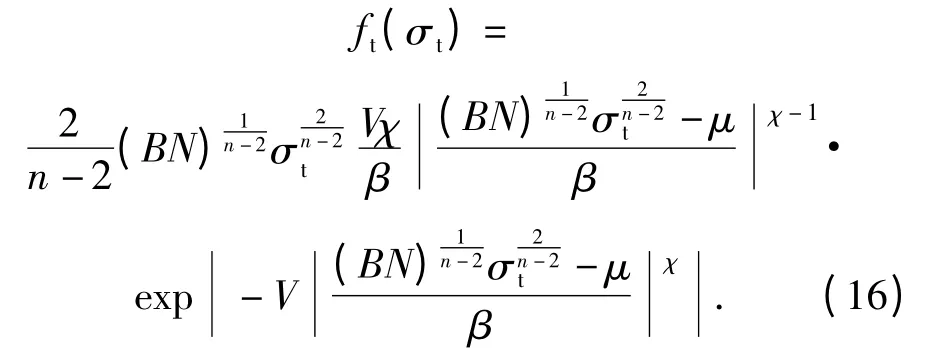
将(16)式代入(5)式可得考虑冲击载荷作用s 次可靠度函数为
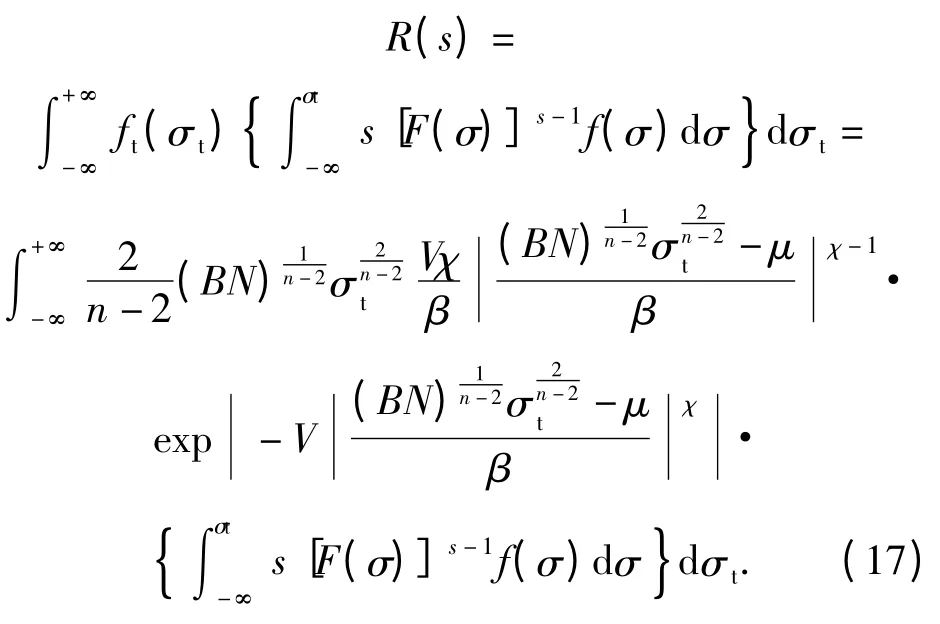
将(16)式代入(7)式可得考虑刀具切削加工时间的动态可靠度函数为
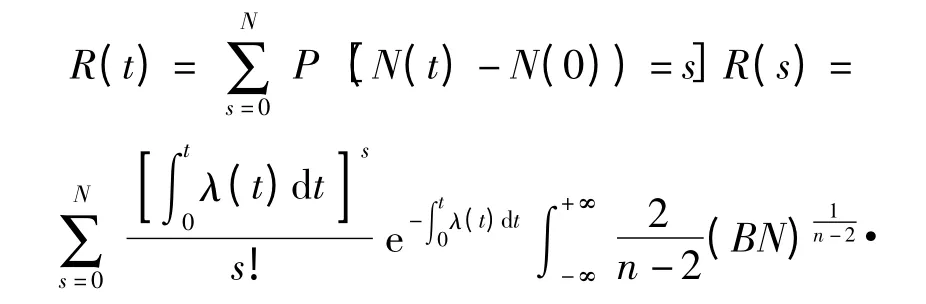
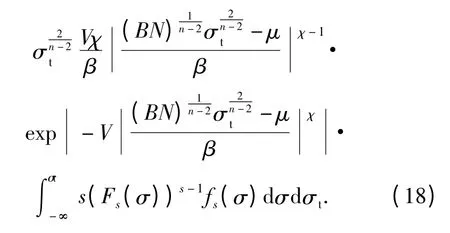
2 硬质合金刀具的动态可靠性灵敏度分析
在切削加工中对方差求灵敏度的物理含义至今还没有统一的定论,所以本文只对参数均值做了灵敏度分析。这里假设基本随机变量向量X =(V β χ μ σt)T,Z=(n Y A KIC)T.基本随机变量向量X、Z的均值E(X)和E(Z)是已知的,可以认为基本随机变量是相互独立的随机变量。通过理论分析,考虑冲击载荷作用次数下的刀具动态可靠性灵敏度分别为(19)式和(20)式;考虑刀具切削加工时间的刀具动态可靠性灵敏度分别为(21)式和(22)式:
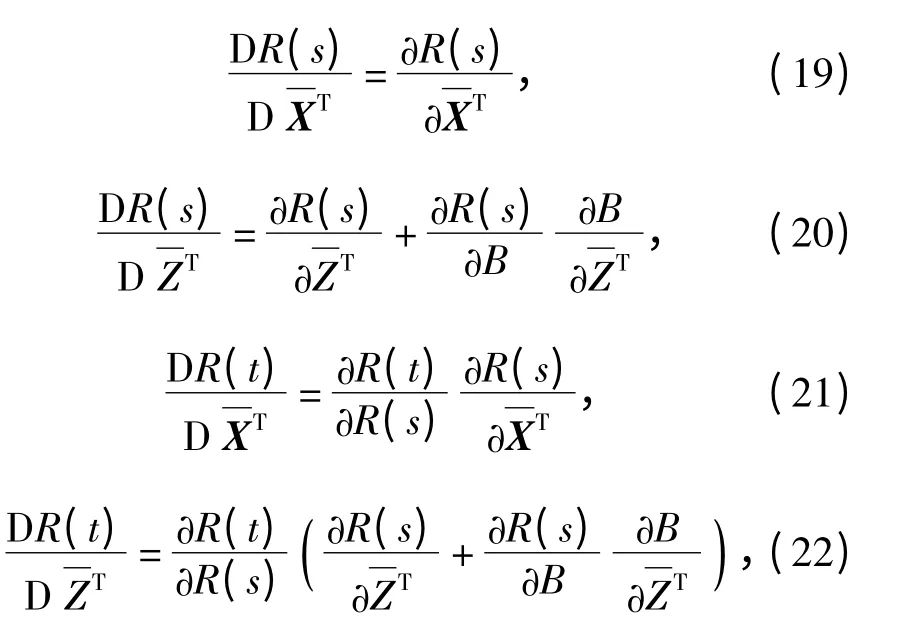
式中:
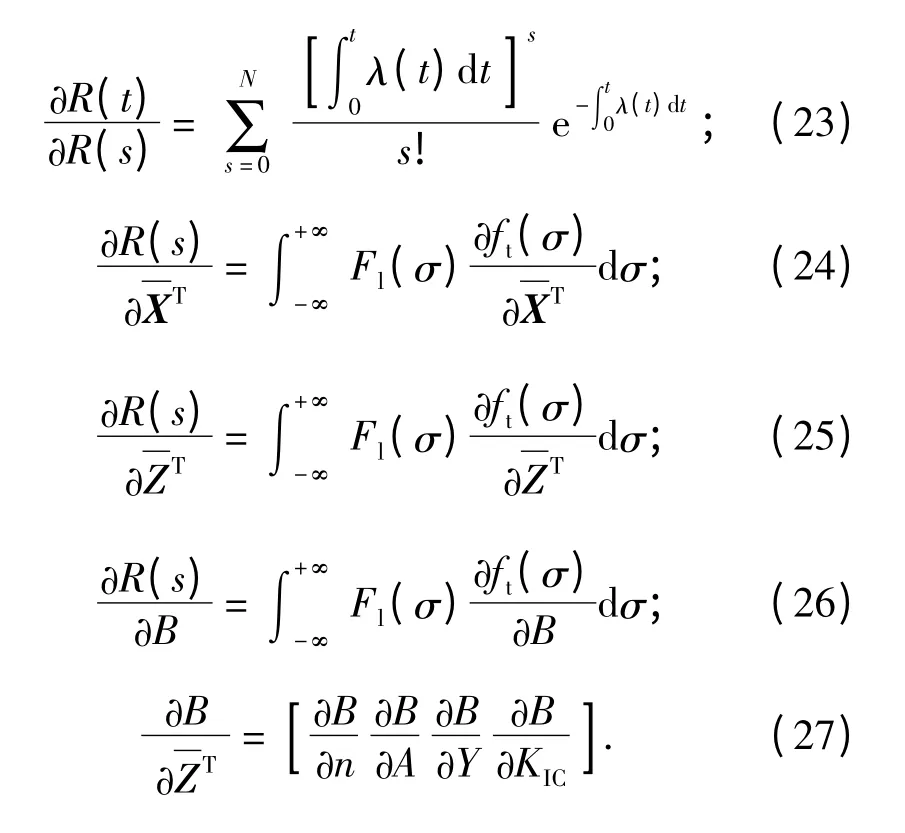
当某参数的可靠性灵敏度数值为正值时,说明随着该参数均值的增加,其结果将使刀具趋于更加可靠。而当某参数的可靠性灵敏度数值为负值时,则说明随着该参数均值的增加,其结果将使刀具趋于更加不可靠(失效)[14-15]。对可靠性灵敏度绝对数值较大的参数,其变化率较大,对刀具可靠度最为敏感,在参数选取时应加以控制,以提高刀具可靠度和被加工零件的精度。
3 测试与理论分析
测试条件:CL-15 数控机床;工件材料为45#淬硬钢,HRC51 ~52 ;工件组装后外圆直径130 mm;刀具材料为YT05 硬质合金,密度12.5 ~12.9 g/cm3,HRA92.5;刀具几何参数为γ0= -5°,α0=6°,λs=-5°,KR=75°,K'r=15°,γ01= -20°,br1=0.1 mm;切削用量为v = 1.6 mm/s,f = 0.15 mm/r,ap=0.35 mm;刀具其他设计参数为KIC均值11 MPa·m1/2,标准差0.06 MPa·m1/2;A 的均值5.6 ×10-15,标准差2.4×1026;Y 的均值1.16,标准差0.88;n 的均值13,标准差1.6;V 的均值1.045 mm3,标准差0.68 mm3;β 的均值1,标准差0.002;χ 的均值2,标准差0.04;μ 的均值200,标准差8.98.
通过测试与分析,在切削过程中所受到的冲击载荷作用次数与时间的关系服从参数λ(t)=26 min-1的泊松随机过程。通过有限元分析可知刀具内部危险位置的应力大小服从均值E(σ)=660 MPa、方差Var(σ)=40 MPa 的正态分布;刀片抗弯强度的形状参数、尺度参数和位置参数服从(3.008,1.336)、(130.68,98.662)、(880,560)的正态分布,刀具寿命N=20 000.考虑冲击载荷作用次数下的刀具对各参数的动态可靠性灵敏度如图1和图2 所示。考虑刀具切削加工时间的刀具可靠度对各参数的灵敏度如图3 和图4 所示。
从图1 ~图4 中可以看出,随着冲击载荷作用次数和切削加工时间的增加,各参数的灵敏度也逐渐增大。R(s)和R(t)对参数V、σt、A、Y 和KIC的灵敏度大于0,随着其均值增加,结果将使刀具趋于更加可靠。对参数n、β、χ 和μ 的灵敏度小于0,随着其均值增加结果将使刀具趋于不可靠(失效)。参数σt和KIC的灵敏度数值较大,是最敏感的两个参数。工程设计人员从图1 ~图4 中可以迅速地确定影响刀具可靠度的参数,并对该参数进行直接或过间接的控制。例如参数V和σt可通过改变切削用量来直接实现参数的控制;参数n 和A 可通过间接改变切削环境温度、切削液和介质来实现参数控制等,以便保证刀具在工作时的高可靠度。
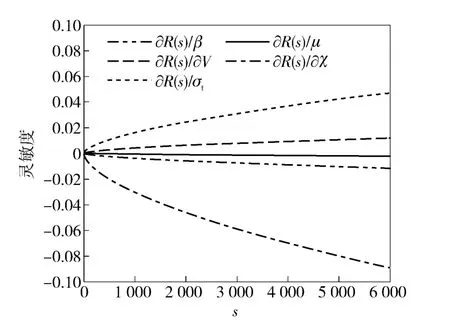
图1 R(s)对参数V、β、χ、μ 和σt的灵敏度曲线Fig.1 R(s)as functions of V,β,χ,μ and σt with the increase in impact loading time
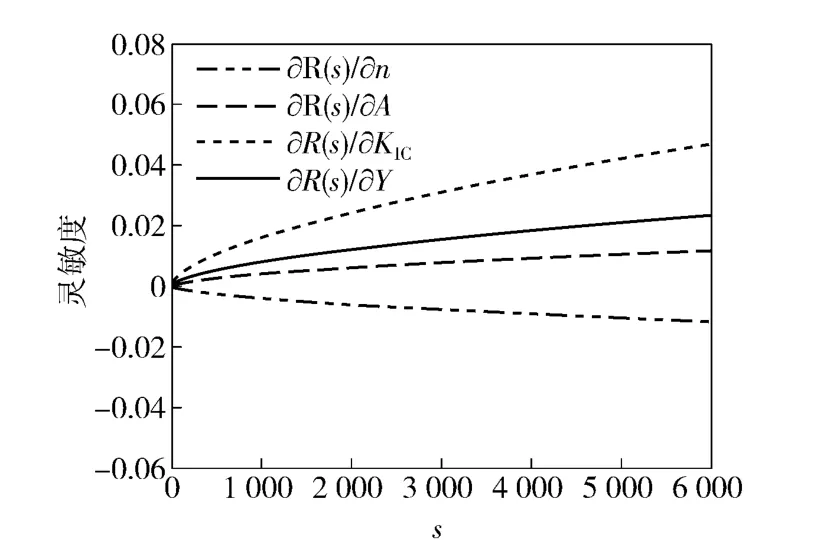
图2 R(s)对参数n、A、Y 和KIC的灵敏度曲线Fig.2 R(s)as functions of n,A,Y and KIC with the increase in impact loading time
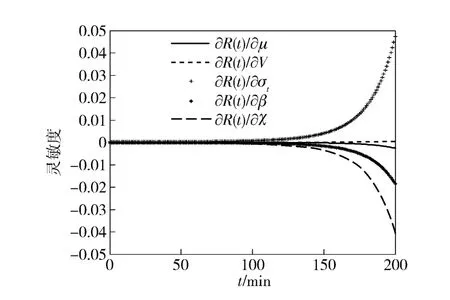
图3 R(t)对参数V、β,χ,μ 和σt的灵敏度曲线Fig.3 R(t)as function of v,λ,χ,μ and σt with the increase in machining time
4 结论
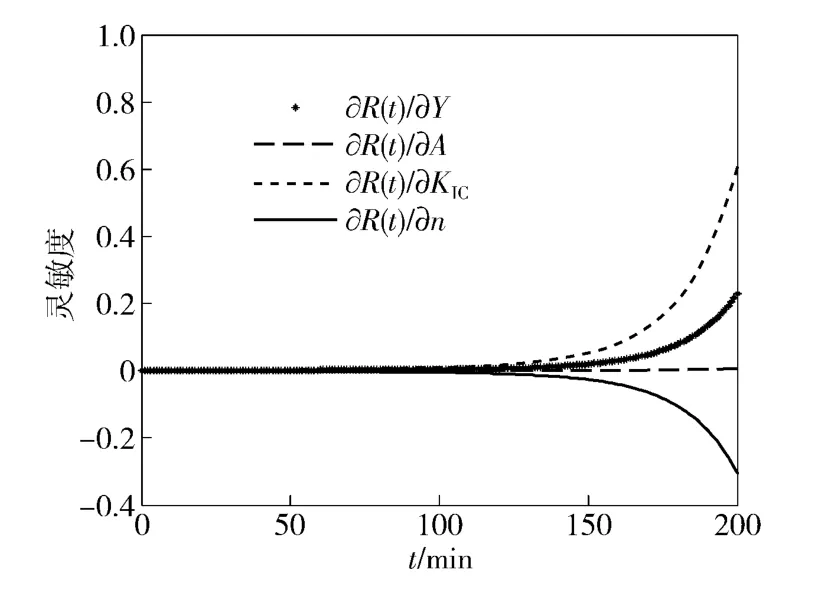
图4 R(t)对参数n、A、Y 和KIC的灵敏度曲线Fig.4 R(t)as function of n、A、Y and KIC with the increase in machining time
1)本文提出了以刀具内部的最大拉应力超过材料的临界疲劳应力作为刀具失效的判据,只需要测出切削力,便可利用本文给出的动态可靠度计算方法求出在不同切削条件下的硬质合金刀具的动态可靠度,对预测刀具寿命有实际的指导意义。
2)本文推导出了硬质合金刀具的动态可靠性灵敏度计算方法,给出了刀具物理参数和材料参数的变化对刀具整体结构可靠性的影响程度,为合理确定刀具设计参数和加工条件奠定了理论基础。
3)随着切削加工时间和冲击载荷作用次数的增加,刀具对各参数的敏感程度也逐步增大。特别是敏感参数的变化将影响刀具的可靠度。对敏感参数应直接或间接加以控制,使刀具可靠性对这些敏感参数的变动不敏感,来达到提高刀具可靠度的目的。
References)
[1]LIU Z Q,LI Z Q,AI X.Study on the life distribution of cemented carbide tools[J].Cemented Carbide,1995,12(1):7 -10.
[2]LI Z Q,DENG J X,HUANG C Z.A tool reliability model under combined effects of s several failure mechanisms[J].Journal of Shandong University,1995,25(3):201 -206.
[3]金雅娟 张义民 张艳林.基于鞍点逼近的机械零部件可靠性及其灵敏度分析[J].机械工程学报,2009,45(12):102 -107.JIN Ya-juan ZHANG Yi-min ZHANG Yan-lin.Analysis of reliability and reliability sensitivity for machine componentsby meanvalue virst order saddlepoint approximation[J].Journal of Mechanical Engineering,2009,45(12):102 -107.(in Chinese)
[4]李常有,张义民,王跃武.恒定加工条件及定期补偿下的刀具渐变可靠性灵敏度分析方法[J].机械工程学报,2012,48(12):162 -168.LI Chang-you,ZHANG Yi-min,WANG Yue-wu.Gradual reliability and its sensitivity analysis approach of cutting tool in invariant machining condition and periodical compensation[J].Journal of Mechanical Engineering,2012,48(12):162-168.(in Chinese)
[5]Wu Y T,Mohanty S.Variable screening and ranking using sampling-based sensitivity measures[J].Reliability Engineering and System Safety,2006,91(6):634 -647.
[6]Li Z Q,Tian Z,Ai X.Stochastic model for tool wear and its application in tool reliability test[J].Journal of Mechanical Engineering,1994(4):7 -11.
[7]Lee Y M,Sampath W S,Shaw M C.Tool fracture probability of cutting tools under different exiting conditions[J].ASME,1984:168 -170.
[8]王新刚,张义民,王宝艳.机械零部件的动态可靠性分析[J].兵工学报,2009,30(11):1510 -1514.WANG Xin-gang,ZHANG Yi-min,WANG Bao-yan.Dynamic reliability analysis of mechanical components[J].Acta Armamentarii,2009,30(11):1510 -1514.(in Chinese)
[9]王正,谢里阳,李兵.考虑失效相关的系统动态可靠性模型[J].兵工学报,2008,29(8):985 -989.WANG Zheng,XIE Li-yang,LI Bing.Dynamic reliability model of the system with dependent failure[J].Acta Armamentarii,2008,29(8):985 -989.(in Chinese)
[10]王新刚,张义民,王宝艳.机械零部件的动态可靠性灵度分析[J].机械工程学报,2010,46(10):187 -193.WANG Xin-gang,ZHANG Yi-min,Wang Bao-yan.Dynamic reliability sensitivity analysis of mechanical components[J].Journal of Mechanical Engineering,2010,46(10):187 -193.(in Chinese)
[11]王正,谢里阳.不确定性载荷作用下的零件时变可靠性模型[J].航空学报,2009,30(7):1243 -1247.WANG Zheng,XIE Li-yang.Iime-variant reliability model of components under uncertain loads[J].Acta Aeronautica et Astronautica Sinica,2009,30(7):1243 -1247.(in Chinese)
[12]Yang J,Fan Y X,Yu T.Theoretical analysis and experimental study on improving the reliability of cemented carbide tools[J].Machine Tool & Hydraulics,2002(6):74 -79.
[13]杨俊茹,李兆前.确定硬质合金刀具可靠度的理论研究[J].山东大学学报:工学版,2003,33(3):235 -237.YANG Jun-ru,LI Zhao-qian.Theoretical study on reliability of cemented carbide tool[J].Journal of Shandong University:Engineering Science,2003,33(3):235 -237.(in Chinese)
[14]张义民,刘巧伶,闻邦椿.汽车零部件可靠性灵敏度你计算和分析[J].中国机械工程,2005,16(11),1026 -1029.ZHANG Yi-min,LIU Qiao-ling,WEN Bang-chun.Reliabilitybased sensitivity computation and analysis of automobile components[J].China Mechanical Engineering,2005,16(11),1026-1029.(in Chinese)
[15]Wang X G,Zhang Y M,Wang B Y.Reliability-based design of automobile components[J].Journal of Mechanical Engineering Science,2009,223(C2):483 -490.

