典型装药水下爆炸的殉爆规律研究
鲁忠宝, 胡宏伟, 刘 锐, 杨 帆
典型装药水下爆炸的殉爆规律研究
鲁忠宝1, 胡宏伟2, 刘 锐1, 杨 帆1
(1. 中国船舶重工集团公司 第705研究所, 陕西 西安, 710075; 2. 西安近代化学研究所, 陕西 西安, 710065)
针对典型的壳装炸药殉爆更接近炸药实际使用状态, 采用ANSYS/LS_DYNA软件建立了典型装药水下殉爆的有限元仿真模型, 通过计算得到了殉爆距离与安全距离, 基于此加工了试验样弹, 并进行了相应的水下殉爆试验。试验结果与数值仿真结果较为吻合, 表明了本文的仿真模型能够有效描述带壳装药的水下殉爆情况, 水下试验中由冲击波压力和气泡周期来判断被发装药是否殉爆是可行的。最后, 在水下殉爆理论分析基础上, 根据试验结果预计了大药量水中兵器战斗部的安全性。本文的研究可为水中兵器战场环境的安全性设计提供依据, 并可为水中兵器战斗部殉爆毁伤能力评估提供参考。
水中兵器; 战斗部; 水下爆炸; 殉爆; 有限元仿真模型; 安全性
0 引言
炸药作为一种含能物质, 在受到足够强的外界刺激如力、热、光和电等作用时会发生爆炸, 并可能造成临近炸药的殉爆[1]。炸药殉爆主要有裸装炸药殉爆和壳装炸药殉爆2类, 其中壳装炸药殉爆更接近炸药实际使用状态。根据所处的环境, 主要有空气中殉爆与水下殉爆2类。目前, 国内外对炸药空气中的殉爆研究较多, 如Howe等人采用欧拉程序2DE对壳装炸药殉爆进行了2D数值仿真[2]; Lu 等人对裸装PBXN2109炸药殉爆进行了数值仿真[3]; Fisher等人对壳装PBXN29 炸药殉爆进行了数值仿真[4]; 陈朗等人计算了不同距离下裸装炸药的殉爆距离[5]; 文献[6]的表1中, 给出了当主发药和被发药均为柱状TNT散装单质炸药时的殉爆试验数据; 王晨等人进行壳装固黑铝(GHL)炸药殉爆试验[7]; 周保顺等对冲击波作用下炸药殉爆过程进行了数值仿真并进行了试验验证[8]。不过, 对炸药水中殉爆研究尚未见详细报道。
对于水中兵器, 战斗部水下爆炸可能激起一定距离上的另一水中兵器战斗部发生爆炸, 即产生殉爆, 殉爆也是摧毁敌方水中兵器的作用方式之一。研究典型装药水下爆炸的殉爆机理, 分析水中兵器战斗部对来袭水中兵器战斗部的安全距离与殉爆距离, 可为水中兵器战场环境的安全性设计提供依据, 同时也可为打击水中兵器用的水中兵器战斗部的毁伤威力评定提供一种新方法。
1 水中殉爆的理论分析
1.1 影响水中殉爆的因素
水中殉爆规律很复杂, 引起殉爆的原因可能有主发装药爆炸产生的冲击波、气泡、二次压力波及爆轰产物直接作用等。影响水中殉爆的因素很多, 主要有以下几个方面。
1.1.1主发装药的影响
不同种类主发炸药其爆炸能量释放与输出特性存在差异, 其殉爆距离也不同。相同种类的炸药, 主发装药的药量越大, 能量越高, 被发装药越容易被起爆。主发装药带外壳时, 爆轰产物受到约束, 增大了主发装药的爆轰性能, 使殉爆距离增大。外壳强度越大, 这种效应越显著。
1.1.2被发装药的影响
被发装药对外界刺激越敏感, 殉爆距离越大。装药密度较低时, 也容易殉爆。另外, 外壳对爆轰产物、冲击波和破片有衰减、阻挡作用, 能导致殉爆距离减小。
1.1.3装药的布局
主发装药与被发装药按同轴线的摆放方式比按轴线垂直摆放方式更容易殉爆, 起爆方式对殉爆距离也有影响。
当主发装药和被发装药的种类确定时, 影响殉爆的主要因素为壳体厚度和材料, 壳体厚度和材料都会对冲击波大小产生影响。有研究表明, 带壳装药水下爆炸的冲击波峰值压力随壳厚与装药半径比的增加先增大后减小, 当壳厚装药半径比为0.07~0.08时, 峰值压力随壳厚变化的趋势发生改变, 对主发装药适当的壳体厚度可以增大殉爆距离。但对被发装药, 可能会导致殉爆距离减小。当主、被发装药都带壳体时, 难以判断出壳体对殉爆距离的影响。
1.2 水中爆炸的起爆判据和殉爆阈值
1.2.1水中爆炸的起爆判据
起爆判据是判断主发装药爆炸后, 被发装药是否爆炸的依据, 空气中一般用爆炸产生的特征参量(冲击波超压)或试验现象(残药或见证板的破坏情况)来判别。对于水中爆炸, 被发装药的残药或残留外壳、见证板难于回收, 可采用水中冲击波压力和气泡周期来判断被发装药是否发生爆轰。
1.2.2水中爆炸的起爆阈值
冲击起爆是炸药对压力脉冲的一种动态响应形式。对于均质炸药, 早期认为只要冲击波压力超过临界起爆压力, 炸药就会被引爆。对于非均质炸药, 其起爆阈值既与冲击波压力有关, 又与其持续时间有关。因此, 水中爆炸殉爆的临界起爆判据需要综合考虑临界起爆压力或临界起爆能量, 殉爆临界起爆阈值应符合:>,≥(为冲击波能,为临界起爆能)。
1.3 带壳装药水中爆炸的殉爆相似律



函数的具体形式可通过试验确定, 当以冲击波超压作为判别殉爆的主要参数时, 水中殉爆距离与主发药量、壳体厚度和装药半径(包括主发和被发装药)的比值有关。
2 数值仿真
有限元分析软件ANSYS/LS_DYNA强大的自适应线谱增强算法(adaptive line enhancement, ALE)和Euler算法及炸药的材料与状态方程广泛应用于各种水下爆炸分析中, 相关资料表明[9], ANSYS/LS-DYNA在水中爆炸分析中有很多成功的案例。对炸药水下殉爆试验的数值仿真可以描述炸药在殉爆中的反应规律, 同时能够获得殉爆过程中的细节规律, 在很大程度上可以减少试验数量。
2.1 计算模型
2.1.1 物理模型及算法
炸药装药水下爆炸殉爆模型见图1,为2个装药的中心距,为2个装药的边距。主发装药与被发装药外形尺寸均为f90 mm×90 mm的圆柱体, 装药类型均为GUHL-1, 主发装药包裹有 1.5 mm的铝壳, 被发装药包裹有1 mm的铝壳。
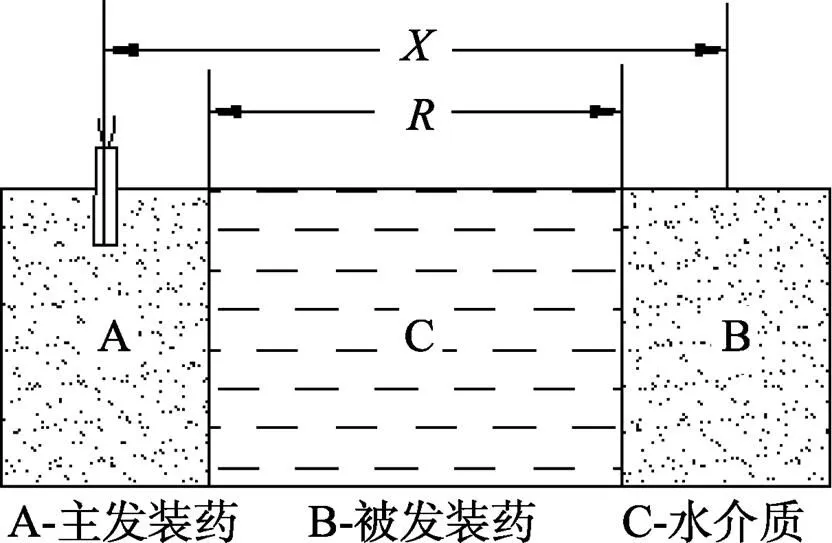
图1 装药水下殉爆示意图
计算模型由主发装药、被发装药、主发装药外壳、被发装药外壳和水介质5部分组成, 其中主发装药、水介质采用欧拉网格建模, 单元使用多物质ALE算法, 被发装药、主发装药外壳、被发装药外壳采用LAGRANGE算法, 在被发装药、主发装药外壳、被发装药外壳与水域间采用关键字*CONSTRAINED_LAGRANGE_IN_SOLID实现耦合算法[10]。主发装药采用圆柱体中心起爆, 根据模型对称性特点, 主发装药及其外壳采用1/2有限元建模。选择SOLID164单元和相应的材料属性对几何模型划分网格, 创建PART, 施加对称约束和透射边界条件, 调整主发装药与被发装药间的距离, 设置求解时间等操作。形成有限元模型如图2所示。

图2 装药水下殉爆有限元模型
2.1.2材料与状态方程
主发装药及被发装药的铝壳选用各项同性随动强化的弹塑性金属材料模型MAT_PLASTIC_ KINEMATIC, 密度=2.7×103kg/m3, 弹性模量=70 GPa,泊松比=0.35, 屈服应力=0.3 GPa; 水选用空白材料模型NULL, 状态方程为EOS_GRUNEISEN, 密度为水=1.025×103kg/m3; 主发装药选用高能炸药燃烧与增长模型MAT_ HIGH_EXPLOSIVE_BURN, EOS_JWL状态方程, 其密度药=1.8×103kg/m3, 爆速=7020 m/s, 爆压P=21.5 GPa, 炸药及水的具体参数可参考文献[11]。被发装药采用流体弹塑性材料模型*MAT _ELASTIC_PLASTIC_HYDRO[12], 采用点火增长反应速率方程*EOS_IGNITION_AND_ GROWTH_ OF_REACTION_IN_HE[12], 方程如下

GUHL-1炸药点火增长模型参数选取如表1所示。
2.2 仿真计算结果
选取几种不同作用距离进行仿真模型的计算。当=3 cm时, 被发装药未被殉爆, 冲击波传播、被发装药变形、被发装药内部#120154单元的压力时程曲线(峰值压力P= 2.31714GPa)见图3。当=1 cm时, 被发装药被殉爆, 冲击波传播、被发装药殉爆、被发装药内部#120154单元的压力时程曲线(峰值压力P=23.224 5 GPa)见图4。

表1 GUHL-1炸药点火增长模型反应速率方程参数

图3 作用距离R=3 cm时, 冲击波传播、被发装药变形以及内部单元压力时程曲线图

图4 R=1 cm时, 冲击波传播、被发装药殉爆以及内部单元压力时程曲线图
3 殉爆试验
按照2.1中的仿真研究模型, 加工了试验样弹, 尺寸都为f90mm×90mm, 装药品种都为GUHL-1, 密度大于1.8×103kg/m3, 主发装药铝壳厚1.5 mm, 传爆药柱为20 g JH-14, 采用8#铜壳电雷管端面中心起爆。被发装药铝壳厚1 mm。
试验水池为圆柱形结构, 试验时将主发装药、被发装药悬吊在水池中心, 入水深度5 m, 并处于同一水平面上, 主发装药和被发装药的距离通过铁丝编制的架子来控制。同时在距爆心2.5 m处布放3个水下传感器, 传感器与两装药处于同一水平面。测定炸药爆炸时水中压力随时间而变化的-曲线。
测试系统由高速采集仪(见图5)、适配器、水下冲击波压力传感器(见图6)、低噪声电缆和专用软件组成。传感器采用美国PCB公司生产的PCB138A型大量程电气石压力传感器, 测量系统有专用软件, 能自动找出气泡脉动周期和冲击波峰值压力等参数。
首先测量了单个1 kg的GUHL-1炸药(主发装药, 见图7)水中爆炸的冲击波压力和气泡周期, 测距为2.5 m, 3点的峰值压力平均值为16.27 MPa, 气泡周期平均值为322.9 ms。GUHL-1和GUHL-1的殉爆试验装配见图8。殉爆的试验结果见表2。

图5 水下数据采集系统

图6 传感器

图7 单个1 kg的GUHL-1炸药

图8 GUHL-1和GUHL-1的殉爆试验装配图
4 结果分析及讨论
针对相同的主发装药、被发装药的水下殉爆研究模型, 采用数值仿真以及试验测试的方式展开研究。
由图4可看出, 在=1 cm时, 被发装药发生膨胀, 其内部一单元的峰值压力达23.224 5 GPa,大于该炸药的爆压P, 被发装药被殉爆; 由图3可看出, 在= 3 cm时, 被发装药发生压缩变形, 内部同一单元的峰值压力仅为2.31714 GPa, 远远小于该炸药的爆压P, 被发装药未被殉爆。同样可得在= 6 cm和= 8 cm工况下, 被发装药均未被殉爆。采用数值仿真方法, 可以明显地观测到被发装药是否被殉爆。数值仿真结果与试验结果的吻合表明, 采用数值仿真方法能较好地模拟水下殉爆, 本文2.1节中的材料与状态方程参数是合理可行的。

表2 GUHL-1和GUHL-1的殉爆试验结果
当殉爆距离较近时, 难以准确测量冲击波峰值压力, 通过数值仿真计算可知, 被发装药GUHL-1的殉爆冲击波压力阈值约为7.49 GPa。
由表2可知, 2个装药表面距离为3 cm, 6 cm和8 cm时, 测点处的冲击波峰值压力和气泡周期与单个1 kg的GUHL-1装药一致, 被发装药未殉爆。2个装药表面距离为1 cm时, 测点处的冲击波峰值压力和气泡周期都大于单个1 kg的GUHL-1装药的冲击波峰值压力和气泡周期, 被发装药殉爆, 与数值仿真结果吻合。研究表明, 在水下殉爆试验中, 由冲击波压力和气泡周期来判断被发装药是否殉爆是可行的。
当主发装药和被发装药都为带壳的1 kg的GUHL-1时, 水中爆炸的殉爆中心距离约为10 cm, 安全中心距离约为12 cm, 距离很近。根据水中爆炸的殉爆相似律可知, 大药量的水中兵器战斗部在水下战场环境下的安全性也很高。
5 结束语
本文选取了水下典型的主发装药与被发装药模型, 采用有限元软件ANSYS/LS-DYNA对典型带壳装药的水下殉爆进行了数值仿真, 并加工了试验样弹, 开展了水下殉爆的试验研究, 得到了典型带壳装药的水下殉爆距离与安全距离。数值仿真结果与试验结果较为吻合, 表明数值仿真模型能够有效描述带壳装药的水下殉爆情况, 试验中由冲击波压力和气泡周期来判断被发装药是否殉爆是可行的。由水下殉爆的理论分析, 可以预计大药量水中兵器战斗部的殉爆安全性。
本文仅选取了典型的水下装药模型, 有关不同装药品种、不同装药形式与起爆方式、不同装药外壳的水下殉爆现象与规律的研究尚没有涉及, 有待后续深入研究。
[1] 章冠人, 陈大年. 凝聚炸药起爆动力学[M]. 北京: 国防工业出版社, 1991.
[2] Howe P M, Huang Y K, Arbuckle A L. A Numerical Study of Detonation Propagation Between Munitions[C]//Pro- ceedings of the 7th Symposium(International) on Detonation, 1982.
[3] Lu J P, Lochert I J, Kennedy D L, et al. Simulation of Sy- mpathetic Reaction Rests for PBXN2109[C]//Proceedings of 13th Symposium(International) on Detonation, 2006.
[4] Fisher S, Baker E L, Wells L, et al. XM982 Excalibur Sympathetic Detonation Modeling and Experimentation
[C]//Insensitive Munitions & Energetic Materials Te- chnology Symposium, 2006.
[5] 陈朗, 王晨, 鲁建英, 等. 炸药殉爆实验和数值模拟[C] //第四届爆炸计算力学会议论文集, 2008.
[6] 李铮, 项续章. 各种炸药的殉爆距离[J]. 爆炸与冲击, 1994, 14(3): 231-241.
[7] 王晨. 壳装炸药殉爆实验和数值模拟[J]. 爆炸与冲击, 2010, 30(2): 152-158.Wang Chen. Experiments and Numerical Simulations of Sympathetic Detonation of Explosives in Shell[J]. Explosion and Shock Waves, 2010, 30(2): 152-158.
[8] 周保顺. 非均质炸药殉爆试验数值模拟[J]. 弹箭与制导学报, 2009, 29(5): 145-148.Zhou Bao-shun. Numerical Simulation of Sympathetic Detonation of Heterogeneous Condensed Explosives[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2009, 29(5): 145-148.
[9] 张胜民. 基于有限元软件ANSYS7.0的结构分析[M]. 北京: 清华大学出版社, 2003.
[10] ANSYS股份有限公司北京办事处. ANSYS/LS-DYNA算法基础和使用方法[M], 2000.
[11] 刘锐. 不同条件下水中爆炸冲击压力场分布特性研究[D]. 北京: 北京理工大学, 2010.
[12] 美国ANSYS公司. ANSYS/LS-DYNA User′s Manual[M], 2003.
(责任编辑: 杨力军)
Research on Law of Sympathetic Detonation of Typical Charge Subjected to Underwater Explosion
LU Zhong-bao,HU Hong-wei,LIU Riu,YANG Fan
(1. The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710075, China; 2. Xi′an Modern Chemistry Research Institute, Xi′an 710065, China)
Aiming at typical charge in shell, a finite element analysis (FEA) model of sympathetic detonation of typical charge subjected to underwater explosion is established using the simulation software ANSYS/LS_DYNA. The distance of sympathetic detonation and the distance of safety are achieved by calculation, and a prototype ammunition is manufactured for underwater sympathetic detonation experiment. The experimental result indicates that the FEA model can describe the underwater sympathetic detonation of charge in shell effectively, and that explosive pressure and bubble period can be used to estimate the occurrence of sympathetic detonation of acceptor charge. Based on the theoretical analysis of underwater sympathetic detonation, the warhead security of typical underwater weapon is estimated according to the experiment result. This study may give a reference for the safety design and the destroy ability evaluation of underwater weapon warhead.
underwater weapon; warhead; underwater explosion; sympathetic detonation; finite element analysis(FEA) model; security
TJ630.1; TP391.9
A
1673-1948(2014)03-0230-06
2013-12-16;
2014-01-27.
鲁忠宝(1978-), 男, 硕士, 高级工程师, 主要从事水中兵器战斗部的研究与设计.

