汽车同步器换挡二次冲击的动态仿真*

李晓春,褚超美，缪 国

(1.上海理工大学机械工程学院，上海 200093；2.上海汽车变速器有限公司，上海 201800)

前言

汽车同步器是保证平顺换挡和延长变速器寿命的重要部件，广泛应用于手动变速器和机械式自动变速器中。由于同步器输出端具有较大的当量转动惯量，而输入端的当量转动惯量相对较小，工作时又受到搅油阻力矩和密封件摩擦阻力矩等因素的影响，所以同步结束后，输入端与输出端会产生新的角速度差，造成齿套与接合齿圈啮合过程中锁止面之间发生碰撞，产生二次冲击现象。严重时会引起噪声和振动，甚至使同步器主要工作部件加剧磨损，进而导致脱挡，影响换挡平顺性和同步器的工作寿命[1-2]。

同步器主要零部件的结构较为复杂，而且整个换挡过程的时间较短，所以很难利用物理样机试验的方法来进行研究[3]。为实现同步器二次冲击的动态仿真，本文中借助动态仿真软件ADAMS建立虚拟样机，研究同步器换挡二次冲击现象。重点分析花键齿端锁止角与棱线角对二次冲击力峰值的影响，为评价二次冲击力峰值提供参考。

1 同步器换挡二次冲击分析

为了研究同步器换挡二次冲击，对同步器的工作过程进行分析。根据同步器的工作过程建立ADAMS动态仿真模型。

1.1 同步器换挡过程分析

本文中对某型乘用车变速器惯性式单锥面同步器3挡升4挡过程进行仿真分析。该同步器主要由齿套、齿毂、锁环、接合齿圈和滑块组等零部件构成，各零部件均按设计要求进行参数化建模。其中滑块组包括滑块、钢球和弹簧等。

同步器整个换挡过程可分为预同步、锁止、解锁、自由滑行和啮合等5个阶段。

同步器的主要工作部件为齿套、锁环和接合齿圈，在整个换挡过程中，三者的位置关系如图1所示。图1(a)为初始位置；开始换挡时，齿套受到拨叉的轴向推力，带动钢球和滑块一起轴向运动，当滑块前端面与锁环突耳接触后，推动锁环与接合齿圈的摩擦锥面接触，在轴向力作用下产生摩擦力矩，使锁环快速转过半个齿宽，完成预同步；图1(b)中ω代表输入端角速度；轴向力使齿套压下钢球迅速与锁环锁止面接触，进入锁止阶段；图1(c)中，摩擦力矩Ms大于作用在锁止面上的拨环力矩Mr，齿套受到锁环阻挡而不能继续轴向移动；随着齿套与锁环角速度差的逐渐减小，当Ms≤Mr时，齿套在轴向力作用下拨开锁环，完成解锁阶段；图1(d)中，直到两部件的锁止面脱离接触，即虚线位置；拨环后齿套不再受锁环阻碍而快速滑行，直至与接合齿圈的锁止面接触；图1(e)为完成自由滑行阶段；图1(f)表示齿套与接合齿圈的锁止面接触后到完成换挡的啮合阶段，虚线位置为其最终位置。

1.2 同步器换挡二次冲击动态仿真

根据同步器工作过程中各零部件的运动形式，利用ADAMS/view建立动态仿真模型，为各零件赋予属性与名称，设置约束和接触，如表1所示[4]。

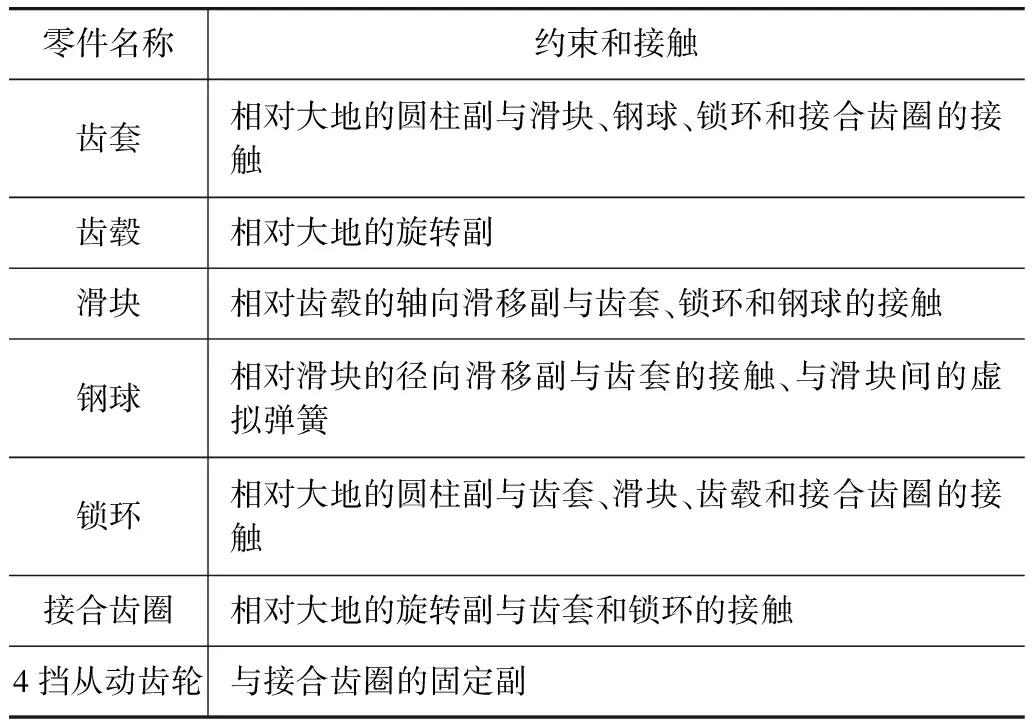
表1 设置约束和接触

建立二次冲击仿真模型如图2所示，仿真结果如图3所示。i,ii,…,v表示上述换挡过程的5个阶段。其中各零件间的接触采用冲击函数法求解，冲击函数方程为

(1)

式中：Fn为冲击力；k为接触刚度；g为切入深度；e为力指数；STEP为阶跃函数；dmax为最大阻尼系数；cmax为最大摩擦因数；dg/dt为切入速度。

乘用车的典型换挡力转换成同步器齿套上的当量轴向力Fax为510N；换挡时发动机转速ne为3 000r/min；单锥面平均工作半径Rc为33.5mm；锥面间摩擦因数μCD为0.08；锥面半锥角α为6.5°；被同步端当量转动惯量IR为4 457kg·mm2；i3和i4分别为3挡和4挡的传动比，则理论同步时间[5]为

(2)

仿真得到同步结束时刻为0.027 6s，由式(2)求得理论同步时间约为0.028 5s，由于在ADAMS的计算过程中考虑了物体在接触受力时发生弹性变形的实际情况，因而产生误差，约为3.2%，小于5%，与同步器实际工作情况基本相符。

2 花键齿参数对二次冲击力峰值的影响

2.1 换挡二次冲击产生机理

同步结束后同步器输入端与输出端产生新的角速度差，造成了齿套和接合齿圈非同步啮合而引起碰撞，即二次冲击。

解锁阶段和自由滑行阶段是影响二次冲击的主要阶段，而影响这两个阶段的同步器主要设计参数为花键齿端锁止角和棱线角，因而重点分析两者与二次冲击力峰值的关系。

2.2 花键齿端锁止角对二次冲击力峰值的影响

花键齿端锁止角是影响二次冲击力峰值的主要参数之一，包括：齿套锁止角β1、锁环锁止角β2和接合齿圈锁止角β3，如图4所示。

为保证同步器正常工作，要求β1≥β2=β且满足如下锁止条件[5]：

(3)

式中：μ1为锁止面静摩擦因数；μ为锥面静摩擦因数；r为锁环工作半径；R为锥面平均半径；β为锁止角值。

解式(3)不等式得105°≤β≤167°，结合目前实际生产要求，选择β值为100°、105°、110°、115°、120°和125°进行分析。同步器齿套为钢制件，锁环为铜制件，可取β1=β2=β。为便于换挡，取β3值小于β，本文中β3取定值95°。以β为变量，齿套、接合齿圈和锁环的棱线角取“s7c7r7”组合，对同步器二次冲击进行仿真，获得齿套和锁环锁止角对同步器二次冲击的影响，如图5所示。

图5(a)为齿套和锁环锁止角取不同β值时齿套质心位置变化的仿真结果。由图可见，当锁止角为100°(小于下限105°)时，预同步结束后齿套迅速穿过锁环，质心位置由3mm处快速运动到8mm处，之后经过一段波动后直接运动到9.5mm处，未出现平直的锁止阶段，即同步器失去锁止能力，因而会产生更大的二次冲击力；当锁止角在105°～125°范围内时，质心位置曲线均出现平直的锁止阶段，即同步器均能完成锁止；取不同锁止角时，分析自由滑行阶段曲线可知，β为115°时齿套质心位置在6.25mm处，移动距离最短。

图5(b)为齿套和锁环锁止角取不同β值时角速度随时间的变化曲线。由图可见，在0.03s之前，3条曲线近乎重合，说明齿套和锁环锁止角的变化对接合齿圈的角速度基本上没有影响，而它们与水平方向的点划线(齿毂角速度)交点对应的时刻即同步结束时刻，约为0.027 6s，与理论同步时间非常接近。角速度曲线在预同步阶段和锁止阶段重合度很高，说明锁止角对预同步阶段和锁止阶段无明显影响。同步结束时刻对解锁阶段和自由滑行阶段无明显影响，即对二次冲击峰值无显著影响。

图5(c)为齿套和锁环锁止角取不同β值时，二次冲击力峰值时间历程的仿真结果。由图可见，齿套和锁环的锁止角对同步器二次冲击力峰值的影响较为显著。随着锁止角的增大，二次冲击力峰值先减小后增大，当锁止角为115°时峰值最小。

2.3 花键齿端棱线角对二次冲击力峰值的影响

目前国内外的研究主要考虑锁止角对二次冲击力峰值的影响，但齿端棱线角对二次冲击力峰值也有较大的影响。定义棱线角分别为齿套棱线角φ1、接合齿圈棱线角φ2和锁环棱线角φ3，如图6所示。现阶段同步器产品的花键齿端棱线角通常取值为0°～9°，本文中结合目标产品的设计要求，取φ1和φ2的值为6°、7°和8°，取φ3值为7°和8°进行研究。

分别以φ1、φ2和φ3为设计变量，β1=β2=β取值为115°，分3组对同步器二次冲击力峰值进行仿真，即第1组以φ1为变量，选取最佳值作为第2组仿真常量，再以φ2为变量，最后以φ3为变量。齿端棱线角对二次冲击的影响如图7所示，图中“s”表示齿套，“c”表示接合齿圈，“r”表示锁环，数字表示棱线角的角度取值。

图7(a)为齿套、接合齿圈和锁环的齿端棱线角取3种不同组合时，接合齿圈和齿毂的角速度随时间的变化曲线。由图可知，不同棱线角组合得到的角速度曲线几乎重合，说明改变齿套、锁环或接合齿圈的棱线角对同步结束时刻基本上没有影响，且与上节仿真结果相同(0.027 6s)。

截取解锁阶段与自由滑行阶段质心位置变化仿真曲线如图7(b)所示。当锁环棱线角比齿套和接合齿圈的棱线角稍大时，齿套质心位置轴向变化较小，自由滑行距离较短，因而碰撞引起的冲击较小。

图7(c)～图7(e)为二次冲击力峰值仿真结果。由图7(c)可知，φ2、φ3取值为7°，φ1为变量，当其为7°时二次冲击力峰值最小；由图7(d)可知，取φ1、φ3角度为定值，φ2为变量，当其为7°时二次冲击力峰值最小；由图7(e)可知，取φ1、φ2角度为定值，φ3为变量，当其为8°时二次冲击力峰值最小。综上所述，当棱线角取值为φ1=φ2=7°，φ3=8°时，产生的二次冲击力峰值最小。

3 同步器换挡二次冲击力峰值评价

为保证变速器换挡的平顺性满足设计要求，对二次冲击力峰值进行评价。文献[6]中将二次冲击力峰值与换挡力峰值的比值定义为二次冲击力峰值系数，来衡量二次冲击的影响程度：

K=FB/Fa

(4)

式中：K为二次冲击力峰值系数；FB为二次冲击力峰值；Fa为换挡力峰值，即当量轴向力Fax，设为定值510N。

根据前面第2.2节和第2.3节的部分仿真结果，即图5(c)和图7(c)～图7(e)所示的二次冲击力峰值数据，按式(4)算得对应于不同锁止角和不同棱线角组合的二次冲击力峰值系数，结果如图8所示。图中横坐标的数据点序号对应的锁止角和棱线角组合见表2。

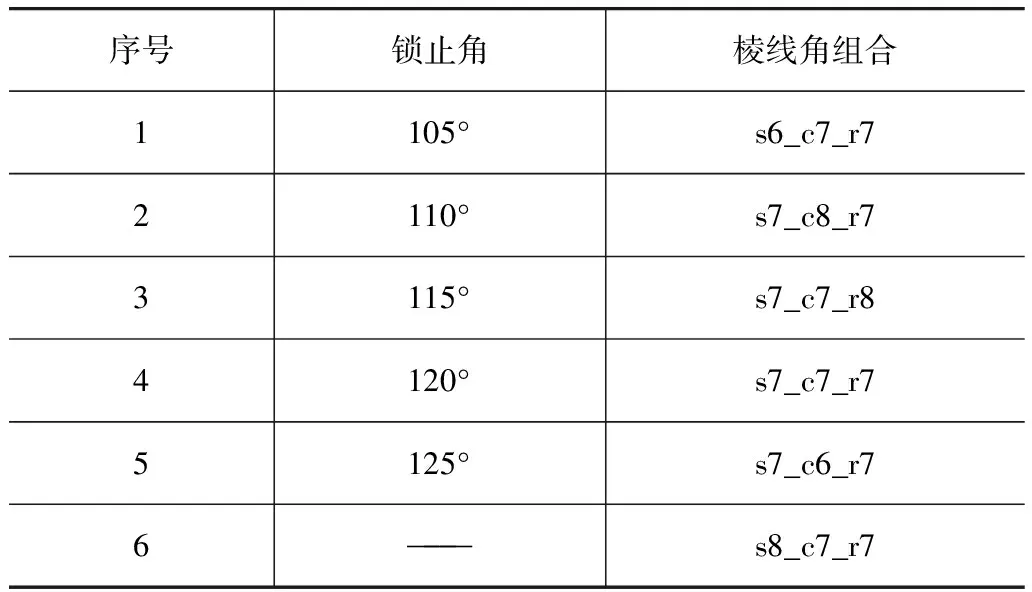
表2 锁止角与棱线角分组列表

由图可见，锁止角取115°，棱线角组合为“s7_c6_r7”时，K值在60%以内，二次冲击可以接受；而锁止角取115°，棱线角组合为“s7_c7_r8”和“s7_c7_r7”时，K值在40%以内，二次冲击更为理想。

4 结论

(1) 当锁止角的取值满足锁止要求时，改变锁止角对同步结束时刻无显著影响，但对二次冲击力峰值影响较大。

(2) 棱线角组合对二次冲击力峰值有较显著的影响。

(3) 最终以二次冲击力峰值系数为评价指标，获得锁止角为115°，齿套、接合齿圈和锁环的棱线角分别为7°、7°和8°为最佳设计参数组合。

[1] Amit Sandooja,Rohit Kunal.Automotive Synchronizer with Asymmetric Toothing[C].SAE Paper 2011-01-0724.

[2] Hiroaki Hoshino.Simulation on Synchronization Mechanism of Transmission Gearbox[C].International ADAMS User Conference,1998.

[3] Hiroaki Hoshino.Analysis on Synchronization Mechanism of Transmission[C].SAE Paper 1999-01-0734.

[4] 陈震,钟再敏,章桐.基于ADAMS的同步器同步过程仿真分析[J].汽车工程,2011,33(4):340-344.

[5] 王望予.汽车设计[M].北京:机械工业出版社,2003.

[6] Manish Kumar Sharma,Jinesh Savla.Shift System Inertia Mass Optimization Techniques to Minimize Double Bump for Manual Transmission[C].SAE Paper 2012-01-1999.