混沌逃逸粒子群优化算法在WSN 覆盖优化中的应用

潘丽姣，吴红英

(义乌工商职业技术学院，浙江义乌， 322000)

0 引言

无线传感器网络(wireless sensor networks，WSN)是一种由大量能量有限的微型传感器节点通过自组织形式形成的网络，它往往部署于环境恶劣、人不易到达的地方，且不易对节点更换电池或充电。WSN覆盖关系到节点的分布，分布越均匀，覆盖率越高，因此，覆盖优化的目标就是在足够覆盖监测区域条件下，尽可能延长网络生存时间，对WSN应用至关重要［1］。如何寻找最优的WSN覆盖优化算法，保持整个网络能量的平衡，成为当前研究的热点［2］。

针对WSN节点覆盖优化问题，国内外学者进行了广泛而深入的研究，提出了大量的WSN节点覆盖优化算法。传统覆盖优化算法包括图论和探测算法，图论算法假设WSN监测区域内，任意位置均能找到一个节点，这与WSN实际部署情况不一致，没有什么实际应用意义;探测覆盖优化算法只适合于小规模的WSN，对于现代大规模WSN，无法获得覆盖率高的方案［3］。随着人工智能技术发展，学者们提出了基于遗传算法、人工鱼群算法、模拟退火算法、粒子群优化算法、蚁群算法等WSN传感器节点覆盖优化算法，相对于传统优化算法，智能算法可以获得更优的覆盖方案，使整个网络节点的分布更加均匀，能量利用率更高，整个网络生存周期得到延长［4－7］。尤其是粒子群优化(particle swarm optimization，PSO)算法具有参数设置少，全局搜索能力强等优点，在WSN覆盖优化应用最为范围。然而，在实际应用过程中，标准PSO算法易早熟收敛，陷入局部最优解，局部搜索能力差，影响其在WSN覆盖优化中的应用［8］。

为了获得更优的WSN传感器节点覆盖率，克服标准粒子群优化算法存在的缺陷，提出一种混沌逃逸粒子群优化(chaotic escape particle swarm optimization，ECPSO)算法的WSN覆盖优化方法，并通过具体仿真对比实验验证算法的性能。

1 无线传感器网络覆盖模型

1.1 WSN传感器节点覆盖优化问题描述

设WSN的节点si的坐标为(xi，yi)，目标区域为二维矩形区域，则节点si对目标点p(xp，yp)的检测概率为

(1)式中:Rs和Re分别为传感器节点感知半径和通信半径;λ1，λ2，β1，β2是与传感器节点特性相关的测量参数;d(si，p)为传感器节点si与目标点p的欧氏距离;

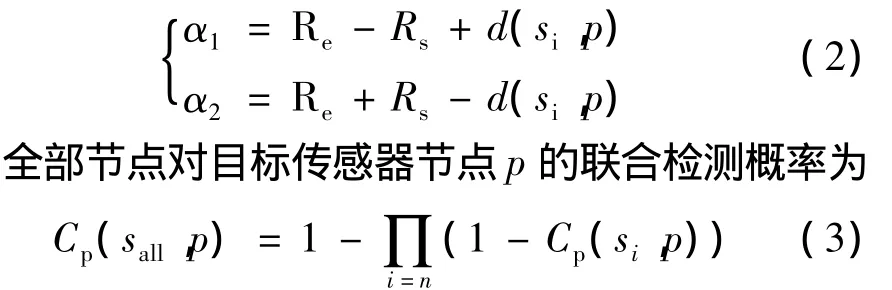
(3)式中，Sall表示测量目标传感节点集合。

设无线传感器目标节点可以被检测到的概率阈值为Cth，那么，传感器目标节点能被检测到的限制条件为

1.2 WSN传感器节点覆盖优化的数学模型

为了有效评价整个无线传感器网络的覆盖率，将无线传感器监测区域划分为m×n个网格，然后将网格简化成为像素点。在本研究中，WSN传感器节点覆盖率定义为满足(4)式要求的网格数量与监测区域网络数量之比，即:

(6)式中:|S'|表示工作传感器节点数;|S|为所有传感器的节点数。考虑到无线传感器网络能量消耗均衡性，引入如下2个定义。

1 )区域能量Ek。将无线传感器监测区域均匀分为K个网格，该网格能量等于该网格中全部传感器节点的剩余能量与该网格中全部传感器节点个数之比，即

(7)式中:mk为第k个网格中的传感器节点数目;Eki为第k个网格中传感器节点i的剩余能量。

2 )能量均衡系数Ea。Ea计算公式为

Ea描述了传感器网络区域间能耗均衡程度，Ea越小，能耗越均匀，反之，能耗越不均匀。

在最优覆盖节点集选取基础上，增加一个能量均衡系数子函数，用于描述网络的能量均衡性，即令f3=Ea。综合考虑传感器节点的覆盖率、工作节点数和能量均衡，在满足一定覆盖率基础上，既节省能量消耗并保持能量均衡，因此，将WSN覆盖优化的目标函数定义为

综合上述可知，要找到最优WSN覆盖方案，实质就是要找到最优的w1，w2和w3以及节点位置。本研究通过采用混沌逃逸粒子群优化算法对(9)式进行求解，找到最优WSN传感器节点覆盖方案。

2 混沌逃逸粒子群优化算法

2.1 标准粒子群优化算法

在标准PSO算法中，每一个粒子代表待求解问题的一个潜在解，适应度函数确定粒子的优劣程度。首先随机产生一群粒子，然后计算粒子的适应度值，最后粒子在解的空间不断飞行，最终找到问题的解［9］。

分别表示粒子i当前的位置和速度，pbest和gbest分别为粒子自身和群体经历过的最好位置，那么粒子速度和位置更新公式为

(10)式中:c1，c2为加速度系数;k为当前迭代次数;r1和2为［0，1］的随机数;ω 为惯性权重。

设Vmax和Xmax分别表示粒子的最大速度和最大位置，那么对粒子速度和位置采用(12)式和(13)式进行限制，防止越界。

2.2 混沌逃逸粒子群优化算法

一个粒子若发现一个当前最优位置，其他粒子就迅速向其聚集，如果该最优位置为一局部最优点，那么粒子群出现“早熟”现象，陷入局部最优。混沌具有对初始条件敏感性、遍历性、随机性等特点，利用混沌运动的这些性质帮助粒子群逃逸局部最优。要帮助粒子群逃逸局部最优，最为关键就是判断何时出现“早熟”收敛现象，本文通过粒子群体多样性和平均适应度进行判断。

1 )粒子群多样性。设粒子飞行空间对角线的长度为L;粒子群大小为m，所示问题的解空间维数为p;pid表示粒子i的第d维坐标值，pd表示粒子群第d维坐标的增均值，那么粒子群的多样性可以采用(14)式描述。

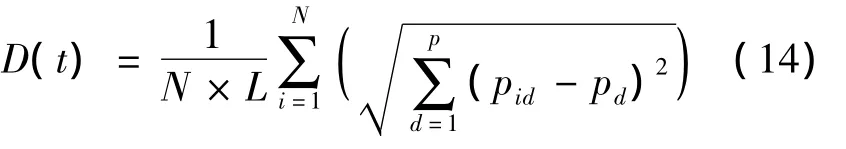
对(14)式进行分析可知，D(t)越大表示粒子群越分散，相反粒子群越集中。

2 )粒子群的适应度方差。随着粒子群不断迭代，粒子间差异变小，粒子间差异由适应度值判断，因此可根据粒子群适应度变化对“早熟”收敛现象进行判断。粒子群的适应度方差σ2定义为

σ2越大，表示粒子群中个体聚集程度越小，反之越大。

当粒子群的D(t)和σ2小于预先给定的阈值时，则表示粒子群可能出现了“早熟”收敛现象，此时，本文采用混沌机制对粒子进行扰动，保证粒子群多样性，使其逃逸局部最优点进而寻找全局最优点。

2.3 粒子群的混沌扰动

一个典型的Logistic方程见(17)式，根据(17)式可知，由任意初值z0，可迭代出一个确定的时间序列 z1，z2，z3，…。

(17)式中，μ为控制参量。

粒子群的混沌扰动过程具体如下:

1 )粒子i的pbesti将通过(18)式映射到(17)式Logistic方程的定义域［0，1］上。

5 )从当前粒子群中随机选择一个粒子，用P*的位置向量代替选出粒子的位置向量。

2.4 ECPSO的WSN传感器节点覆盖优化步骤

1 )设置WSN传感器节点覆盖环境，并随机产生一组初始粒子。

2 )根据(10)式计算每一个粒子的适应度值、初始个体极值Pbestt和群体极值gbest。

3 )根据(10)式和(11)式更新粒子的速度和位置，产生新一代粒子群。

4 )计算新一代粒子群的个体适应度值。

5 )对于每个粒子来说，若粒子适应度值优于自身历史最优值，则用该粒子位置替代个体历史最优位置。

6 )对于每个粒子来说，若粒子适应度值优于群体最优适应度值，则用该粒子位置替代群体历史最优位置。

7 )计算粒子群的D(t)和σ2值，如果小于阈值时，转步骤8)，否则根据正常状态进行，转步骤9)。

8 )对粒子群的最优位置向量进行混沌扰动操作。

9 )若达到最大迭代次数，那么返回全局最优粒子位置，否则跳转步骤3)继续搜索。

10 )输出WSN传感器覆盖的最优解。

3 仿真实验

3.1 仿真环境

为了验证 ECPSO算法的性能，在 MATLAB 2007工具箱进行仿真实验，并与基本PSO算法进行比较。其中Cth=0.65，D(t)，σ2的值根据(14)式和(15)式进行计算。WSN传感器监测区域大小为10 m×10 m的正方形区域，节点感知半径均为1m，20个节点随机分布在监测区域内，节点初始化位置具体见表1。

表1 传感器节点的初始分布Tab.1 Initial distribution of the sensor nodes

3.2 结果与分析

3.2.1 与标准PSO算法的性能对比

PSO和ECPSO算法的WSN节点覆盖方案如图1和图2所示。

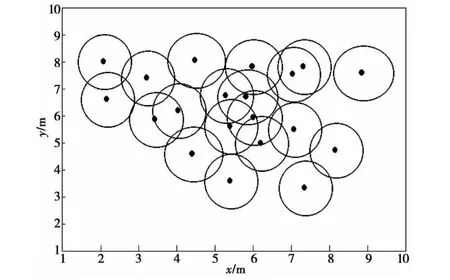
图1 PSO算法的传感器节点分布图Fig.1 Sensor node distribution map of PSO algorithm

图2 ECPSO算法的传感器节点分布图Fig.2 Sensor node distribution map of ECPSO algorithm

在图1和2中，圆表示节点的感知半径，实心点表示节点的位置。对图1和图2进行分析对比得知，PSO算法覆盖方案的节点分布极不均匀，出现大面积重复覆盖。而ECPSO文算法不仅节点覆盖均匀性优于PSO算法，而且重复覆盖区域大幅度减少。仿真结果表明，ECPSO由于引入混沌机制，可以帮助PSO算法逃逸局部最优解，大幅度提高了节点的覆盖率。

3.2.2 与其他优化算法性能对比

对ECPSO算法与其他WSN覆盖优化算法进行对比，在相同环境下，采用遗传算法(genetic algorithm，GA)、人工鱼群算法(artificial fish swarm algorithm，AFSA)、蚁群算法(ant colony optimization algorithm，ACOA)进行对比实验，结果见表2。

从表2可知，ECPSO算法的平均覆盖率要高于对比算法，并且休眠率以及能量均衡性均优于其他算法。搜索最优覆盖方案的速度最快，对比结果表明，ECPSO是一种高效的、覆盖率高的WSN传感器节点覆盖算法。

表2 不同覆盖优化算法的性能对比Tab.2 Performance comparison of different coverage optimization algorithm

4 结束语

覆盖优化是当前WSN中的一个重要研究方向，在分析WSN覆盖优化问题基础上，建立了覆盖优化的数学模型，并提出采用混沌逃逸粒子群优化算法对数学模型进行求解。仿真结果表明，相对其他WSN覆盖优化算法，ECPSO提高了WSN节点覆盖率，重复区域减少，提高了整个WSN网络的性能。

［1］WANG Yang，WANG Ruchuan，CHENG Xi.Improved multipath routing with WNN for the Open Networks［J］.The Journal of China Universities of Posts and Telecommunications，2008，15(2):107－113.

［2］张静，黄宪通，杨新锋.基于传感器网络节点配置优化仿真研究［J］. 计算机仿真，2012，2(11):85－88.

ZHANG Jing，HUANG Xiantong，YANG Xin－feng.Research on Sensor Deployment Based on Probabilistic Detection Model［J］.Computer Simulation，2012，2(11):85－88.

［3］张晋，刘大昕，徐悦竹，等.WSN关键区域覆盖启发式优化算法［J］. 计算机工程，2009，35(14):162－164.

ZHANG Jin，LIU Daxin，XU Yuezhu，et al.Critical Area Coverage Heuristic Optimization Algorithm in WSN［J］.Computer Engineering，2009，35(14):162－164.

［4］李燕君，潘建.无线传感器网络的节点智能部署方法研究［J］.计算机科学，2012，39(8):115－118.

LI Yanjun PAN Jian. Intelligent Node Deployment Scheme for Wireless Sensor Networks［J］.Computer Science，2012，39(8):115－118.

［5］贾杰，陈剑，常杜然，等.无线传感器网络中基于遗传算法的优化覆盖机制［J］.控制与决策，2007，22(11):1289－1301.

JIA Jie，CHEN Jian，CHANG Guiran，ZHAO Lin－liang，et al.Optimal coverage scheme based on genetic algorithm in wireless sensor networks［J］.Control and Decision，2007，22(11):1289－1301.

［6］刘丽萍，李桂丹，王智，等.无线传感器网络多重覆盖算法［J］.天津大学学报:自然科学与工程技术版，2009，42(4):310－314.

LIU Liping，LIGuidan，WANG Zhi，et al.A Weighted Multiple Coverage Algorithm in Wireless Sensor Networks［J］.Journal of Tianjin University:Science and Technology，2009，42(4):310－314.

［7］XU Bo，GUAN Qing，CHEN Ke.Multi－Agent Coalition Formation Based on Quantum－behaved Particle Swarm Optimization［J］.Journal of Information ＆ Computational Science，2010，7(5):1059－1064.

［8］赫然，王永吉，王青，等.一种改进的自适应逃逸微粒群算法及实验分析［J］.软件学报，2005，16(12):2036－2044.

HE Ran，WANG YongJi，WANG Qing，et al.An Improved Particle Swarm Optimization Based on Self－Adaptive Escape Velocity［J］.Journal of Software，2005，16(12):2036－2044.

［9］冯昌利，高雷阜.一种结合混沌和逃逸的自适应粒子群优化方法［J］.计算机工程与应用，2011，47(26):35－38.

FENG Changli，GAO Leifu.Improved adaptive particle swarm optimization method based on self－adaptive escape and chaos［J］.Computer Engineering and Applications，2011，47(26):35－38.

(编辑:魏琴芳)