子矩阵约束下广义反中心对称矩阵的广义特征值反问题
王小雪,程宏伟,杨琼琼,周 硕
(1.东北电力大学理学院,吉林 吉林132012;2.吉化一中,吉林 吉林132022)
1 引 言
矩阵反问题和矩阵特征值反问题是近年来计算数学的重要研究方向之一,在科学和工程技术中具有广泛应用[1-7].矩阵的广义特征值反问题在结构动力学,分子光谱学,结构设计,参数识别和自动控制等许多领域都有重要应用,它主要讨论Ax=λBx成立的条件及通解表达形式[2-5];随着科学技术的发展,有各种各样已有的系统需要改善或扩充,这实际上就是矩阵的扩充问题,矩阵扩充问题即为子矩阵约束下的矩阵反问题,研究矩阵扩充问题对矩阵理论及其实际应用具有重要意义[6-7]。本文应用矩阵对的商奇异值分解[8],研究子矩阵约束下广义反中心对称矩阵的广义特征值反问题及其最佳逼近问题。
Rm×n表示所有m×n实矩阵的集合,ORn×n表示n阶正交矩阵的集合,用rank(A)表示矩阵A的秩,Ik表示k阶的单位矩阵,Sk表示k阶的反序单位矩阵,对A=(aij),B=(bij)∈Rm×n,A*B=(aijbij)∈Rm×n为矩阵A与B的Hadamard积;Rm×n中定义A与B的内积为 <A,B>=tr(BTA),由此内积导出的范数,即为矩阵A的Frobenius范数,并且Rm×n是一个完备的内积空间。
定义1 设P、Q分别是给定的n阶对称正交矩阵,如果A∈Rn×n,满足PAQ=-A,则称矩阵A为关于P、Q的广义反中心对称矩阵。所有n×n阶广义反中心对称矩阵的全体记为ACSRn×n(P,Q)。
显然,矩阵集合 ACSRn×n(P,Q)与矩阵 P、Q 有关,当 P=Q=Sn时,集合 ACSRn×n(P,Q)即为反中心对称矩阵的集合ACSRn×n。全文假定矩阵P、Q是给定的。
本文讨论如下问题:
问题1 给定X∈Rn×m,Λ =diag(Λ1,Λ2,……Λl)∈Rm×m。Λj(j=1,2,……l)为一阶或二阶矩阵,A0∈ Rr×r,B0∈ Rr×r,求矩阵 A,B ∈ ACSRn×n(P,Q),使得

其中A([1,r])是矩阵A的r阶顺序主子矩阵。
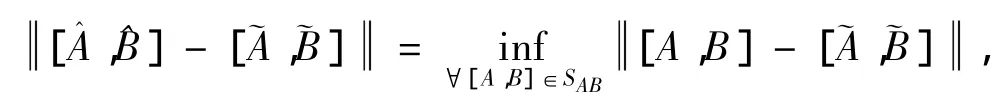
其中SAB为问题1的解集合。
第2节利用商奇异值分解给出了问题1有解A,B∈ACSRn×n(P,Q)的充分必要条件,并在有解的情况下,给出了问题1的通解表示。第3节证明了问题2最佳逼近解[A^,^B]的存在唯一性,并且给出[A^,^B]的表达式。
2 问题1有解的条件及通解表示
引理1 设P,Q∈Rn×n为对称正交矩阵,则存在n阶正交阵U,V,使得P,Q的谱分解为
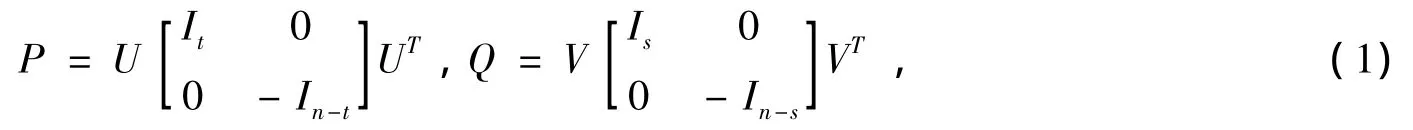
引理2 设A∈Rn×n,P,Q∈Rn×n为对称正交矩阵,且P,Q的谱分解为式(1),则A∈ACSRn×n(P,Q)为广义反中心对称矩阵当且仅当

记
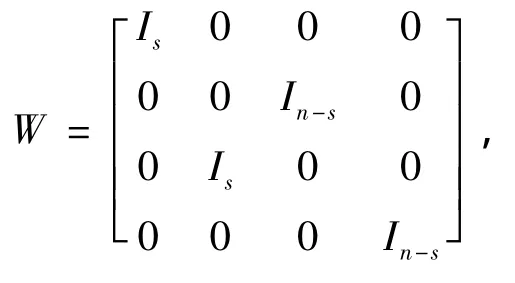
对给定 X ∈ Rn×m,记


其中
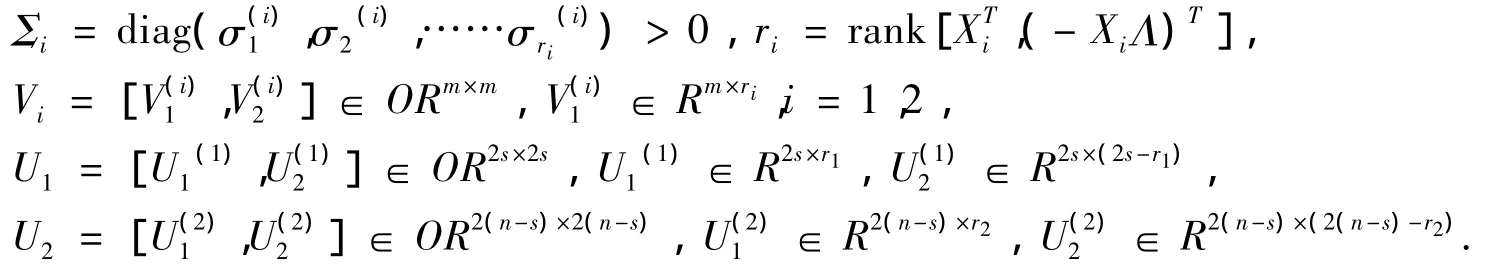
对文献[9]中的定理1进行推广可得如下结论:
引理3 设X∈Rn×m,Λ =diag(Λ1,Λ2,……Λl)∈Rm×m,Λj(j=1,2,……l)为一阶或二阶矩阵,P,Q为对称正交矩阵,则问题AX=BXΛ恒有解A,B∈ACSRn×n(P,Q),且其通解可表示为

其中 G1∈ R(n-t)×(2s-r1),G2∈ Rt×(2(n-s)-r2)是任意矩阵。
由引理3知AX=BXΛ在ACSRn×n(P,Q)中总有解,解的一般形式如(4)式所示,设其解集合为Ω,则求问题1的解等价于求
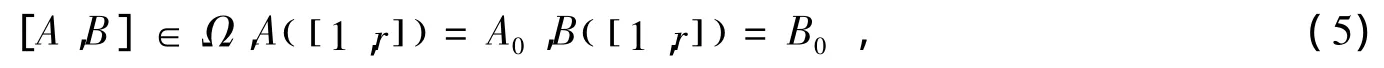
因为A0,B0分别是A,B的顺序主子阵,则

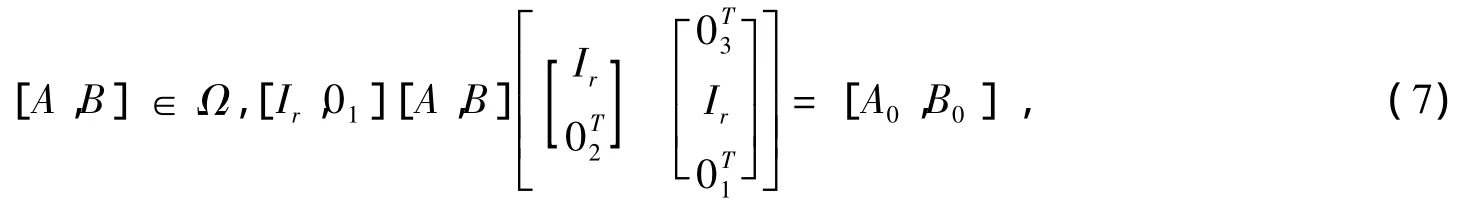
记


将矩阵对W1,W2和分别作商奇异值分解[8](QSVD)

有如下分块形式

这里

C1=diag(a1,a2,……ar4)>0,C2=diag(b1,b2,……br6)>0,0,01,02,03,04为相应阶数的零矩阵;
将(10)式代入(9),得


根据(11),(12)式中 Σi(i=1,2,3,4)的分块形式,将 Y=(Yij)3×3,Z=(Zij)3×3,C=(Cij)4×4进行相对应的分块,则(14)式可化为
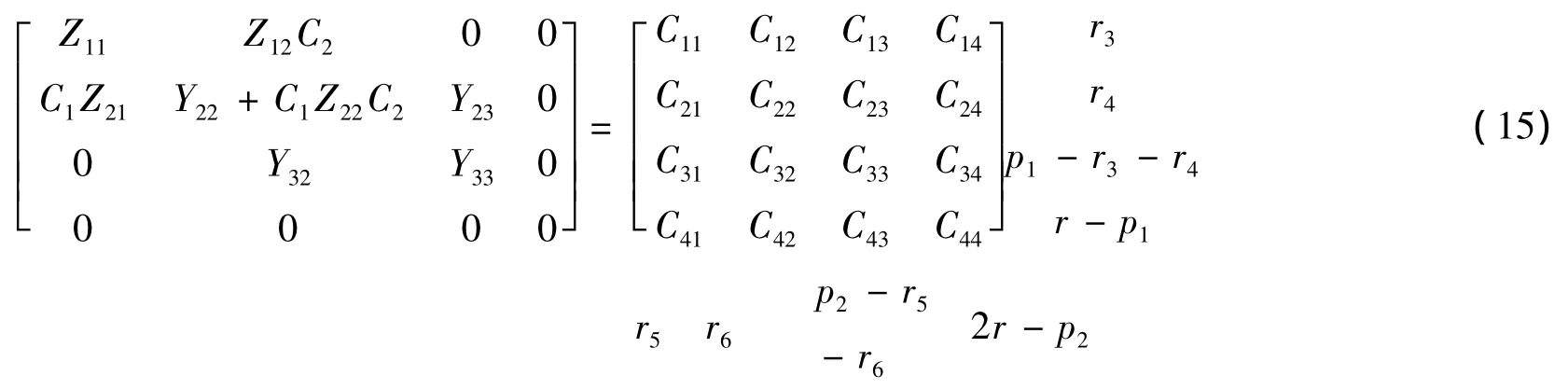
综合上述分析,可得如下定理。
定理1 问题1有解的充分必要条件是

并且在有解情况下,问题1的通解为

其中
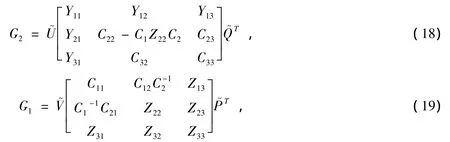
这里 Y11,Y12,Y13,Y21,Y31,Z13,Z23,Z31,Z32,Z33分别为对应阶的任意矩阵。
证明 问题1有解等价于(15)式成立,从而问题1有解的充要条件是(16)式。在有解情况下,由,及公式(3),(15)可得问题1 的通解表达式为(17)式到(19)式。
3 问题2的解
为了证明问题2解的存在唯一性,我们需要如下有限维内积空间的最佳逼近定理[10]。
引理4 设V1是有限维内积空间V的一个闭凸集,则V中任一向量α在V1上存在唯一的最佳逼近。
引理 5[11]给定,则有唯一解
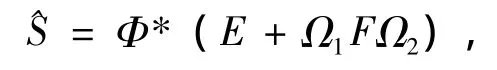

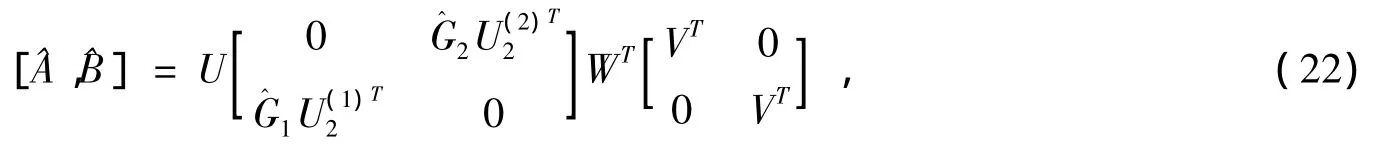
其中
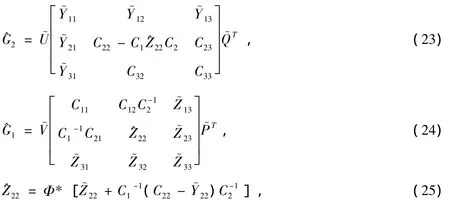
这里
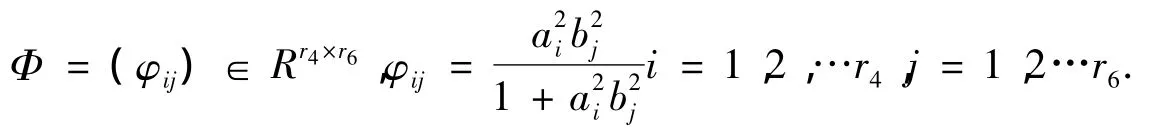
证明 若定理1的条件满足,则SAB非空,且SAB是内积空间Rn×n×Rn×n中的一个闭凸集。由引理4知在 SAB中存在唯一的最佳逼近。由(20)-(21)式及均为正交矩阵,可得

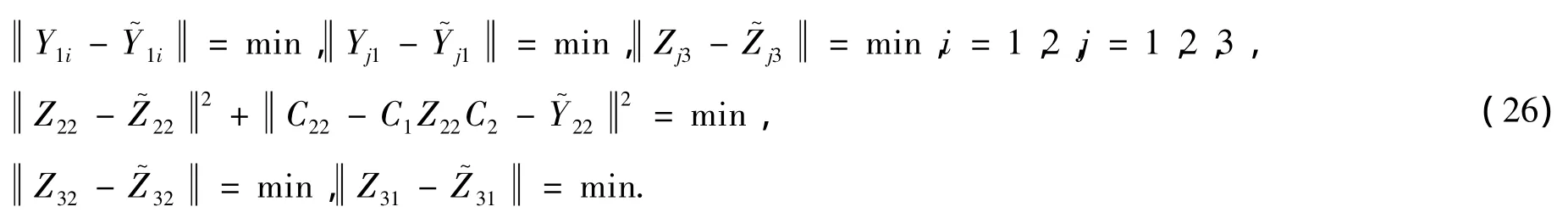
由引理5可得
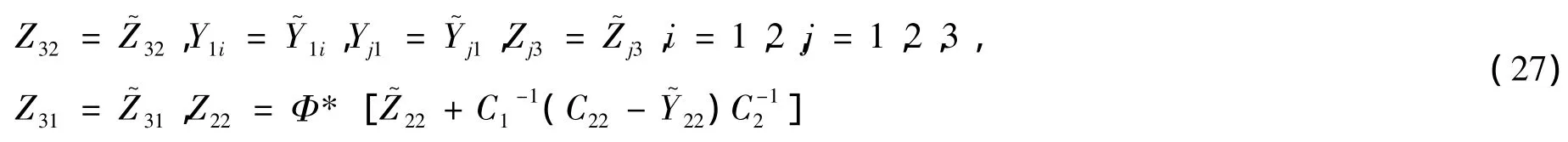
这里

将(27)式代入(17)-(19)式即得(22)-(25)式。
[1]周树荃,戴华.代数特征值反问题[M].郑州:河南科学技术出版社.1991.
[2]邓继恩,王海宁,崔润卿.广义反自反阵的广义特征值反问题[J].河南理工大学学报,2007,26(3):340-344.
[3]王江涛,张忠志,谢冬秀,雷秀仁.埃尔米特自反矩阵的广义逆特征值问题与最佳逼近问题[J].数值计算与计算机应用,2010,31(3):232-240.
[4]周硕,吴柏生.对称正交对称矩阵的广义特征值反问题[J].吉林大学学报:理学版,2006,44(2):185-188.
[5]吴春红,林鹭.自反阵的广义特征值反问题[J].厦门大学学报,2006,45(3):305-310.
[6]龚丽莎.关于子矩阵约束下矩阵方程问题的研究[D].湖南大学.2006.
[7]莫荣华,黎稳.子矩阵约束下的埃尔米特广义反汉密尔顿矩阵特征值反问题及其最佳逼近[J].数学物理学报,2011,31A(3):691-701.
[8]Delin Chu,Bart De Moor.On a variational formulation of the QSVD and the RSVD[J].Linear Algebra and its Applications,2000,311:61-78.
[9]周硕,吴柏生.反中心对称矩阵的广义特征值反问题[J].高等学校计算数学学报,2005,27(1):53-59.
[10]戴华.矩阵论[M].北京:科学出版社,2001.
[11]廖安平.一类逆特征值问题的拓广[J].湖南大学学报:自然科学版,1995,22(2):7-10.

