基于改进组搜索优化算法的输电网规划

聂宏展，段柯均，王 瑞，赵 丹

(东北电力大学输变电技术学院，吉林吉林132012)

输电网起到传输电能的作用，在电力系统中具有不可替代的地位。为了满足日益增长的电力需求与越来越高的供电要求，电力系统的规模不断扩大，电网规模的扩大已成为电网发展的必然趋势。而在满足经济可靠地输送电能的前提下，如何计算出最佳的电网结构，成为电力系统规划中亟待解决的问题。

近年来，智能优化算法被大量应用于大规模输电网规划中，其中差分进化算法［1］、粒子群算法［2］、遗传算法［3］、人工鱼群算法［4］、蚁群算法［5］，这些优化算法的应用有利于快速、准确地获得输电网规划的最优方案。但随着大规模输电网的不断发展，优化问题的维数不断增大，以上优化方法难免出现“维数灾”和“组合爆炸”等问题［6］，往往难于快速求得全局最优解。

组搜索优化算法(GSO)是由S.He等人于2006年提出的一种模拟食肉动物种群觅食策略的优化算法，主要对种群成员间明确的分工行为及分工对应的搜索策略进行模仿。GSO算法采用Producer－Scrounger模型作为框架，文献［7］中证明GSO算法除发现者个数、追随者与巡逻者的比例之外的参数不敏感，这体现出了GSO算法的鲁棒性。而且，GSO算法在已被广泛应用于工程结构优化设计［8］，求解多维函数优化问题［9］等问题中。但目前，还未有相关文献提出将GSO算法应用于求解输电网规划问题中。

基于GSO算法优良的搜索特性，本文首次将组搜索优化算法以及改进型组搜索优化算法应用到求解输电网规划的数学模型中，希望能丰富输电网规划求解思路。但作为一种新的方法，目前的研究还不够深入，还有许多需要研究以及改进的问题。

1 输电网规划模型

本模型以新扩建线路为变量，采用直流潮流方程模拟网络运行，以新扩建线路投资费用、运行时网络损耗费用、正常运行时过负荷惩罚费用以及输电走廊建设费用最小为目标函数并计及系统正常运行时不过负荷为约束的输电网络规划的数学模型可描述为。

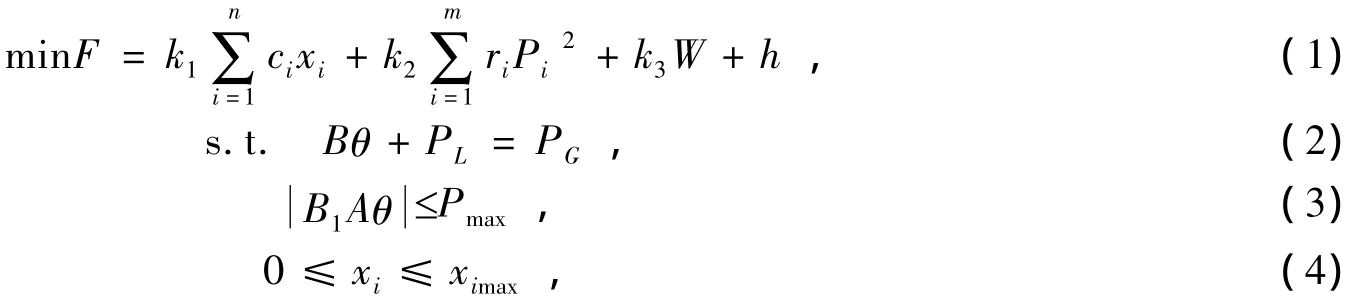
其中，F为规划年建设费用;k1为新扩建线路单位公里的建设费用;ci为第i条新扩建线路的公里数;xi为输电走廊内扩建线路的回路数;k2为网络损耗费用系数;Pi为正常运行时支路i输送的有功功率;Pimax为线路i的传输功率上限;ri为支路i的电阻;k3为过负荷费用惩罚系数;W为模型中总的过负荷量;h为输电走廊的建设费用;B为系统节点导纳矩阵;B1为由各支路导纳组成的对角矩阵;θ为节点电压相角矢量;PL为负荷矢量;PG为发电机出力矢量;A为系统关联矩阵;ximax为支路i可以新增线路的上限。

其中过负荷费用和输电走廊费用如下。

式中:a为输电走廊单位面积费用;w为输电走廊宽度;l为输电走廊长度;Ω为过负荷线路集合;Ψ为扩建线路集合。

本文所采用的评价方法中认为目标函数值越低，规划结果的经济性越好，相应的，适应度值就越高。目标函数值与适应度值成反比的关系。

2 组搜索优化算法(GSO)

组搜索优化算法(Group Search Optimizer，GSO)又称群搜索优化算法，因其独特的种群结构和在处理优化问题时的优异表现，逐渐被人们关注并推广。

GSO算法通过将种群中的寻优个体分为3种角色，即搜索资源并发布资源信息的发现者，向发现者靠近以协助搜索的追随者，在可行域内随机游荡避免算法陷入局部极值的巡逻者。每种角色均具有单独进化的能力，有效地增加了种群进化的多样性。因此相对于其他启发式算法，组搜索算法在处理多变量，大规模，复杂化的输电网规划问题上具有一定优势。三种角色的搜索行为如下:

在n维搜索空间中，第i个个体在第k次迭代过程中的位置可以表示为一个n维的候选解向量

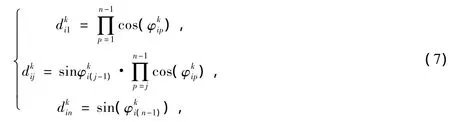
每次迭代中选择种群中适应度最好的成员为发现者，其坐标为XP，它对周围的区域进行局部搜索，其最大搜索角为θmax，最大搜索距离为lmax，那么在第k次迭代时发现者将对如下三个区域执行搜索:

前方区域

右侧区域

左侧区域

式中:μ1∈R1为符合标准正态分布的随机数，μ2∈Rn－1是在(0，1)之间的随机序列。通常θmax为设定参数，lmax的计算公式为:

其中:Ui、Li分别为设计变量取值范围的上界和下界。

发现者根据适应度的优劣，将以上三个区域进行对比，若某位置比当前位置更好，则发现者移动至新的区域。否则，发现者将停留在原位置，只转换一个方向角:

式中:ωmax为最大转换角度，取为π/(n+1)。

如果发现者在α次角度转换后，依然没有发现更好的位置，则搜索方向角变回原方向角:φk+α=φk，式中α是一个常数。

种群剩余成员中80% 被选作追随者，它们将向发现者移动，协助发现者对周围区域进行搜索。对于第k次迭代的第i个追随者，其追随搜索行为可用公式表示为:

式中:μ3∈Rn是(0，1)之间符合均匀分布的随机序列。

此外，对可行域内进行随机搜索，寻找未知资源最有效的角色就是巡逻者。取种群剩余成员中的20% 作为巡逻者。对于第k次迭代的第i个巡逻者，将生成一个随机方向角φi:

式中:ωmax为最大转换角度;然后随机选择一个移动距离:

巡逻者随机移动至新位置:

3 改进组搜索算法(CAGSO)

通过编制GSO算法MATLAB程序并应用于输电网规划后发现GSO算法的角度搜索机制十分复杂，每次迭代初期均需要大量的角度计算，影响搜索效率;发现者搜索行为具有局限性，仅能通过搜索角度的变化搜索左侧，正前方，右侧的区域，无法大面积搜索附近区域。此外，迭代后期追随者行为趋同性严重。由于在GSO算法中，追随者始终以生产者的位置为行动方向，产生候选解。随着迭代的进行，这些候选解趋向于生产者，表现出强烈的趋同性，影响算法对可行域的空间勘探能力。

综合以上分析，本文对应用于输电网规划中的组搜索优化算法进行改进。

改进型组搜索算法(CAGSO)的主要改进如下:

混沌动力学中的Iogistic映射［6］计算简单，参数少，搜索效率高。故摒弃组搜索算法发现者搜索方式中复杂的角度搜索策略，引入Iogistic映射。令k=0;随机生成N维变量t(k)。按照式 t(k+1)=μt(k)(1－t(k))，得到混沌变量t(k+1)。其中，μ为控制变量，μ∈[0，4]，当u=4时，Logistic映射为满映射.此时系统处于完全的混沌状态。依式x*(k+1)=x*+Bt(k+1)对当前最优变量x*进行混沌优化搜索。若f(x*(k+1))＜f(x*(k))，则f*=f(x*(k+1))，x*=x*(k);若 f(x*(k+1))≥f*，则保留上次迭代f*与x*，并重新进行搜索，其中f*为当前最优适应度值，x*为当前最优解，B为一很小的常数。

针对迭代后期，追随者逐步趋向于发现者从而出现趋同性的缺点，通过引入反方向视角搜索策略加以改进。反方向视角策略［10］的引入使成员能以一定的概率做反方向搜索，以增加成员的多样性，提高算法的空间勘探能力，减少算法陷入局部最优的概率。反方向搜索新位置公式如下:

其中，r表示接受反方策略的概率阈值，rand是(0，1)区间的均匀分布随机数。

摒弃角度搜索后，通过引入循环平移因子［13］概念对巡逻者的搜索策略进行改进。循环平移算子Dshift(a，k)表示将向量 a循环平移 m个元素，如Dshift(［1，2，3，4］，2)=［3，4，1，2］。

则巡逻者搜索策略如公式(18)所示:

4 算法流程图

CAGSO算法的流程图，如图1所示。

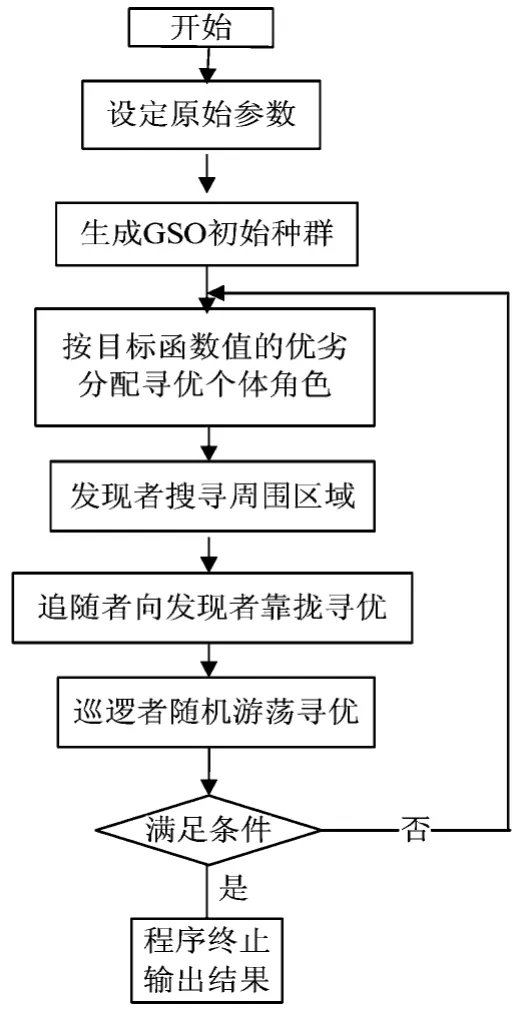
图1 算法框图

5 算 例

5.1 算例1

采用IEEE－18节点系统进行试验，算例网络结构及参数参见文献［4］。根据分析调试经验，对算法中种群个数取为51，初始搜索角度取φ0=4/π，常数a设为对取整数，最大搜索角度取θmax=π/a2，最大转向角度取amax=π/2a2。CAGSO算法中取μ =2，N=33，B取0.05 ～ 0.15的随机数，反方向策略概率阀值r为0.3。过负荷检验采用直流潮流，最后一次迭代生成的发现者的位置信息为最优结果。

应用MATLAB软件进行组搜索算法程序编制并求解，最快通过6.8 s的计算得到最优解，其中输电走廊费用为14051万元，规划方案如下图2所示，这也与最优的网络规划结果一致。

图2 规划结果图

根据文献［11］确定a的取值，取单回线输电走廊综合成本为1.45(元/m2)，取双回线输电走廊综合成本为1.32(元/m2)，取三回线输电走廊综合成本为1.25(元/m2)，取四回线输电走廊综合成本为1.20(元/m2)。根据文献［11］，在220 kV线路中，单回线走廊宽度为48.27 m，2回线走廊宽度为68.27 m，3回线走廊宽度为88.27 m，4回线走廊宽度为108.27 m。

为了论证CAGSO算法的优越性，将其与AFSA与GSO算法进行比较，迭代次数设为1000次，分析结果见表1。通过表1可以看出，经过50次运算，在最优解出现代数和计算时间上，CAGSO算法具有很大的优势，在收敛次数和计算时间上均有较大提升。

表1 结果比较

5.2 算例2

采用巴西南部46节点系统进行试验，算例网络结构及参数参见文献［12］及算例1。

应用MATLAB编制CAGSO算法程序并求解。模型中不计输电走廊费用的最优结果为188 005万元，规划方案如下表2所示:

为了论证CAGSO算法的优越性，将其与GSO算法进行比较，迭代次数均设为1 000次，分析结果如下图4。从图4中可以看出，CAGSO算法在求解巴西南部46节点系统上可以快速求得最优结果，算法在求解大规模规划问题上有很大的优势，而GSO算法收敛速度十分缓慢，收敛过程中多次陷入局部极值。

图3 CAGSO、GSO、AFSA寻优路径比较

图4 CAGSO算法和GSO算法寻优路径比较

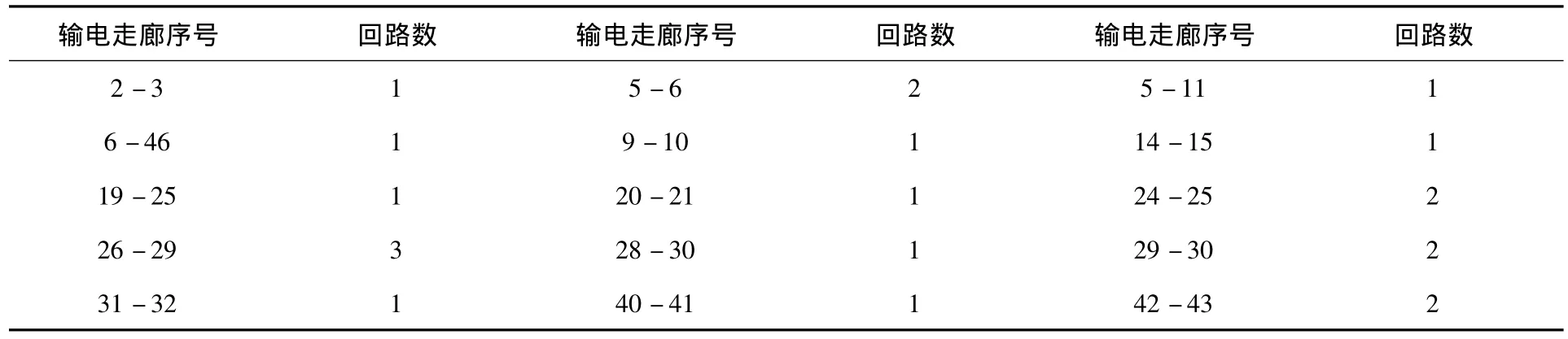
表2 巴西南部46节点系统优化方案

6 结 论

通过将GSO算法与CAGSO算法应用于求解IEEE－18节点系统以及巴西南部46节点的编程试验，并与广泛应用的人工鱼群算法进行比较可以得出:相较于GSO算法与人工鱼群算法，Iogistic模型，反视角搜索策略以及循环平移因子的加入使CAGSO算法拥有更为良好的搜索特性。在寻优过程中，收敛次数少，计算时间短，有效地提高了组搜索优化算法在求解大规模输电网规划问题时的搜索效率。

［1］聂宏展，郑鹏飞，于婷，等.基于多策略差分进化算法的输电网规划［J］.电工电能新技术，2013，32(1):13-18.

［2］金义雄，程浩忠.改进粒子群算法及其在输电网规划的应用［J］.中国电机工程学报，2005，25(4):46-50.

［3］王赛一，王成山.遗传禁忌混合算法及其在电网规划中的应用［J］.电力系统自动化，2004，28(20):43-46.

［4］聂宏展，吕盼，乔怡.基于人工鱼群算法的输电网络规划［J］.电工电能新技术，2008，27(2):11-15.

［5］翟海保，程浩忠，吕干云，等.基于模式记忆并行蚁群算法的输电网规划［J］.中国电机工程学，2005，25(9):17-22.

［6］方振国，陈得宝.新的基于混沌搜索的组优化算法［J］.计算机应用，2011，31(03):657-659.

［7］He S，Wu Q H，Saunders J R.Group search optimizer:An optimization algorithm inspired by animal searching behavior［J］.IEEE Trans.on Evolutionary Computation，2009，13(5):973-990.

［8］李丽娟，黄振华，刘锋.用于结构优化设计的改进多目标群搜索算法［J］.工程设计学报，2013(1):11-17.

［9］任凤鸣，王春，李丽娟.多目标群搜索优化算法及其在结构设计中的应用［J］.广西大学学报:自然科学版，2010，35(2):216-221.

［10］王李进，钟一文，胡欣欣.一种求解多维函数优化问题的改进组搜索优化算法［J］.小型微型计算机系统，2013，34(3).

［11］Haffner S，Monticelli A，Garcia A，et al.Branch and bound algorithm for transmission system expansion planning using a transportation model［J］.Proceedings of the IEEE，2000，147(3):149-156.

［12］詹俊鹏，郭创新，吴青华，等.快速群搜索优化算法及其在电力系统经济调度中的应用［J］.中国电机工程学报，2012，32(1):1-6.