基于相对主元分析的风电机组塔架振动状态监测与故障诊断

周 进，房 宁，郭 鹏

(新能源电力系统国家重点实验室(华北电力大学)，北京市102206)

0 引 言

风电机组安装在户外，工作条件恶劣，导致机组的故障率高。通过有效的状态监测和故障诊断方法能够及早发现风电机组部件的早期故障隐患，避免或减小故障带来的损失，对提高风电场运行的经济性和安全性有重要意义。振动分析是风电机组状态监测的重要方法，用来监视如风电机组齿轮箱、塔架等部件的工作状态［1］。文献［2］利用小波分析具有良好的时频定位特性和对非平稳信号的自适应能力，对风电机组传动链振动信号进行分析和处理。为了克服振动信号调制载波边带重叠和测量噪声的影响，文献［3］首先采用经验模态分解(empirical mode decomposition，EMD)将非平稳的风电机组振动信号分解为基本的固有模态函数，然后对其采用希尔伯特变换，以达到精确识别故障的目的。但在上述文献中，仅对某部件本身的振动信号进行了分析和处理。实际上，风电机组各部件之间存在着严重的机械耦合关系，如叶轮气动特性变化时，塔架受到的载荷会发生变化，进而塔架振动会发生变化［4-9］。本文以某风电场数据采集与监控系统(supervisory control and data acquisition system，SCADA)运行数据为基础，对塔架振动及其影响因素进行详细的分析。采用相对主元分析方法(relative principal component analysis，RPCA)建立塔架与其影响因素之间的关系模型。通过计算监控统计量Hotelling T2(简称T2)和平方预测误差SPE(squared prediction error)的计算实现塔架振动运行数据的分析挖掘，从而实现对其的状态监测与故障诊断。

1 风电机组塔架振动分析

本研究选用的风电机组为变速恒频双馈机组，额定功率为1.5 MW，其切入风速、额定风速和切出风速分别为3，12，25 m/s，额定转矩为880 kN·m。该风电机组的SCADA 采集和记录运行数据的时间间隔为10 min，记录了有功功率、无功功率、风速、桨距角、塔架和传动链振动等多个风电机组的运行参数。通过对这些运行数据的深入分析，能够得到风电机组各个部件的真实运行状态。塔架振动传感器安装在塔筒内壁的顶端，测量塔架振动加速度。传动链振动传感器安装在传动链末端。本文所选用的SCADA 数据为在2011年3 ～5月采集记录的共5 500条记录。大型MW 级风电机组为变速变工况运行，随着风速的改变，机组的运行状态也随时变化。在切入风速和额定风速之间，风电机组工作在最大风能追踪状态，在此风速段，机组的桨距角固定。当风速变化时，通过控制发电机转矩来改变机组的转矩和转速，从而使叶尖速比保持在最佳值附近，使叶轮捕获更多的风能，达到最大风能追踪的目的。

图1 为2011年3月25 ～30 日期间，风电机组工作正常时塔架振动和其他相关SCADA 变量的趋势图。图2 为2011年4月30 日至5月3 日期间，塔架振动和相关SCADA 变量的趋势图。图2 中椭圆标识出的区域中塔架振动出现异常。

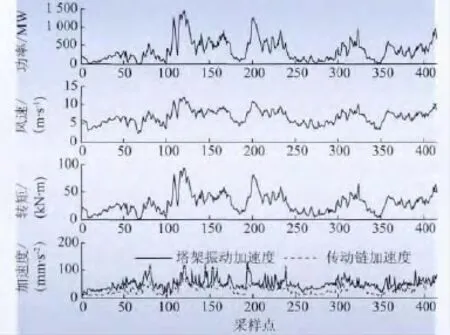
图1 2011-03-25 至2011-03-30 塔架振动及相关变量趋势图Fig.1 Tower vibration and other related variables trend graph from 2011-03-25 to 2011-03-30

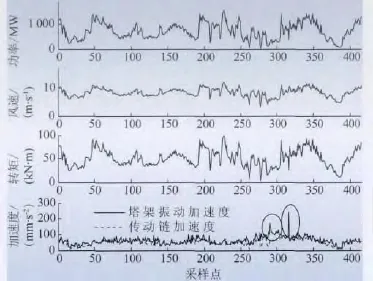
图2 2011-04-30 至2011-05-03 塔架振动及相关变量趋势图Fig.2 Tower vibration and other related variables trend graph from 2011-04-30 to 2011-05-03

在切入风速和额定风速之间，风电机组的桨距角固定不变(为2°)。由图1 可知，塔架振动受以下多个因素的影响:

(1)风速。风电机组的能量来源为风，叶轮是风能转换为机械能的装置，当其受到风的作用时，在叶轮平面内产生气动转矩，使叶轮转动;在机组水平轴向方向上，产生轴向推力和载荷［4］。该轴向推力和载荷与风速近似成正比，激励塔架发生振动。因此，风速变化是塔架振动幅值变化的最重要的影响因素。

(2)转矩和功率。在额定风速以下的最大风能追踪控制方式下，为保持最佳叶尖速比，当风速增大时，机组的设定转矩和功率也随之改变，传动链上的旋转部件如齿轮箱的转速也相应升高，振动加剧，进而导致塔架振动也相应增大。

(3)传动链振动。塔架作为机舱和传动链的支撑部件，机舱内的传动链振动会传递给塔架，这也是塔架振动的重要激励源之一［10-11］。

2 塔架振动建模

2.1 塔架振动监测

在SCADA 数据中，塔架振动与其他多个变量之间不是孤立的，而是存在密切的相关关系，这种相关关系是由风电机组的运行方式决定的。塔架振动建模是利用SCADA 中记录的风电机组正常运行时的数据，建立塔架振动与其相关变量之间的复杂隐含关系。建立的塔架振动模型能够反映机组正常运行时多个变量之间的关系，可以作为标尺，来监测和发现风电机组在运行中的早期异常变化和故障。

本文采用RPCA 方法，将风电机组正常运行时SCADA 数据中记录的塔架振动和其相关变量风速、转矩、功率、传动链振动等变量组成样本作为相对主元模型的输入和建模数据。机组正常运行时的RPCA 塔架振动模型完成后，输入1个当前时刻的输入量时，可以实时计算出2个统计量SPE、T2及其阈值。当这2个统计量超出阈值时，预示风电机组运行出现异常［11］。

2.2 塔架振动建模方法

传统的主元分析(principle component analysis，PCA)方法在进行塔架振动的监测时会存在以下问题:

(1)计算出系统多变量序列构成的协方差阵特征值，再依据特征值的大小来确定各级主元。然而，特征值与对应分量的数据残差或误差的大小密切相关，同时残差或误差的大小又与相应分量所使用的量纲密切相关。由于量纲的不同，使传统方法中误差大的量不一定就是对系统起主导作用的分量。

(2)选取主元的个数以及其代表性是由数据间的关系决定，因此只有从相关性高的数据中提取的主元才具有更大的代表意义。在上述情况下，提取有代表性的主元时会遇到困难，不能有效地建立主元模型。

针对传统PCA 方法存在的问题，本文采用RPCA 方法［11-14］建立塔架模型。

记X 为变量数为N，采样样本数为n 的某系统的数据矩阵

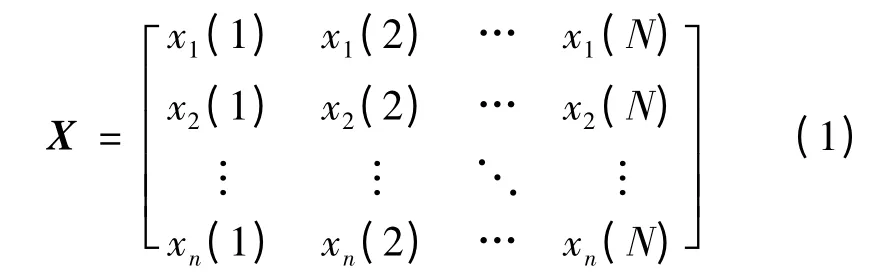
对其进行相对变换，得到:

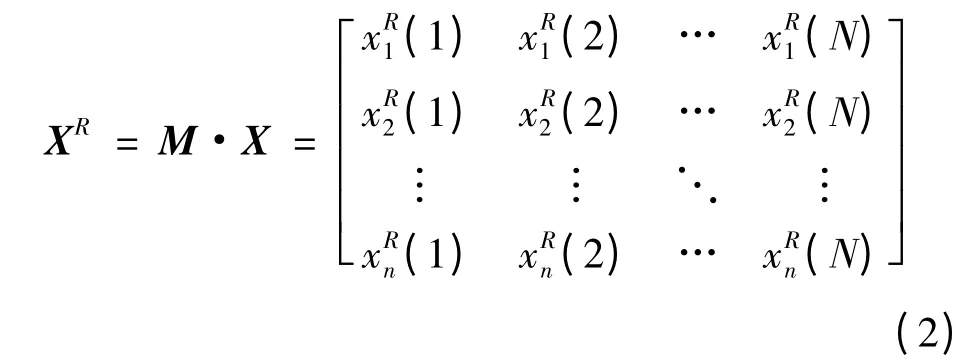
式中xiR= mixi，mi= μiωi＞0。μi为比重因子，是一种根据实际系统而定的先验信息，分别作用在每个变量上，其大小体现了相应分变量在系统中的相对重要程度;ωi是对应随机变量的标准化因子，根据系统的不同，标准化选择方式也有多种，可以根据下列原则来确定相对化变换算子M:

(1)相对化变换能够使系统变量序列构成的数据尽量摆脱分布均匀的现象。

(2)经相对化变换后求取的相对主元更具有代表性和表征系统变化的能力，相对化变换后系统的能量保持不变或者能量为原来系统的倍数，即

经相对变换后的随机矩阵XR，不仅保持了原随机变量间的相关性，摆脱了原有分布均匀的现象，而且使主元的选取更加容易，从而能进行更有效的特征提取、数据压缩和故障诊断等工作。

采用PCA 或者RPCA 方法进行性能监控时，通常是利用监测主元空间的Hotelling T2统计量和残差空间的SPE 统计量来获取整个生产过程运行状况的实时信息。其中，SPE 统计量反映了在某一时刻测量值对模型的偏离程度;而T2统计量是通过主元模型内部主元向量模的波动来反映变量的变化情况，反映的是采样数据在主元平面上的映射点与多变量数据均值之间的距离［15］。采用RPCA 方法进行过程监控和故障诊断的流程如图3 所示。

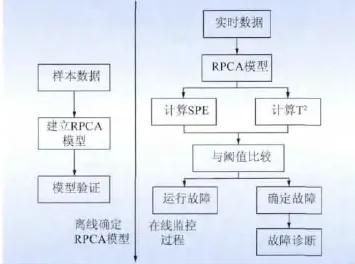
图3 RPCA 过程监控和故障诊断算法的实现模型Fig.3 Implementation model of process monitoring and fault diagnosis algorithm for RPCA

3 塔架振动模拟

根据2011年3月25 日至2011年5月30 日期间机组的报警和停机记录，将机组故障停机或切入风速以下的低风速停机时段的SCADA 记录从建模数据集中剔除，得到正常工作状态下各变量的运行数据(图1 为部分正常运行数据)，采用这些数据建模并求其主元。继而对2011年4月30 日至2011年5月3 日，即图2 数据所在时间段的415个数据进行检测与诊断。

图4、5 是采用传统PCA 进行分析得出的结果。图4 的阈值为25.47，图5 的阈值为0.79。由图4、5可知在316 点SPE、T2统计量的值超过阈值且远远大于其他采样点的值，可以判断在此点出现了故障。但由于T2统计量描述了由前K个主元所解释的数据的综合波动程度;SPE 统计量描述了未被主元模型所解释的数据变化，是对数据在残差空间中的描述，故SPE 统计量对数据的变化会表现得比较敏感，致使图5 中在316 点之前出现了一些误报点，即SPE 统计量超出了设定阈值。

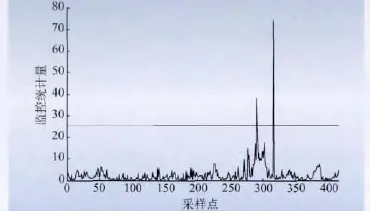
图4 PCA 的T2 统计量监控图Fig.4 T2 statistic monitoring chart of PCA

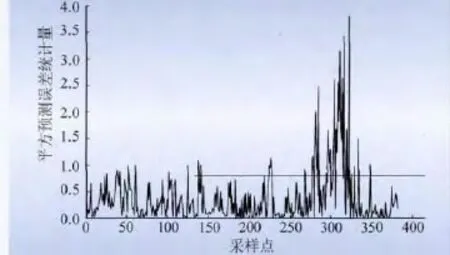
图5 PCA 的SPE 统计量监控图Fig.5 SPE statistic monitoring chart of PCA

为使主元更具有代表性，并消除这些误报点，在进行RPCA 分析时，将比重因子设为1 ∶1 ∶1 ∶0.8 ∶1.1，得到图6、7。通过对比图5 与图7，可以看到SPE 图中大量误差点已被消除，验证了RPCA 方法的有效性。从图6、7 中可看出:从275 点开始，T2统计量和SPE 统计量已经持续不断地超过阈值，预示实际运行数据已出现异常，偏离正常的塔架模型特性。

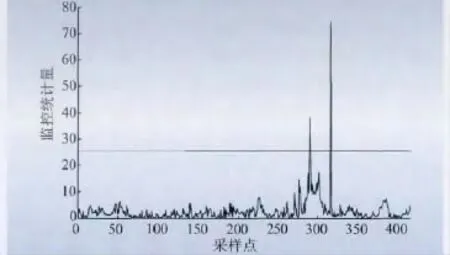
图6 RPCA 的T2 统计量监控图Fig.6 T2 statistic monitoring chart of RPCA

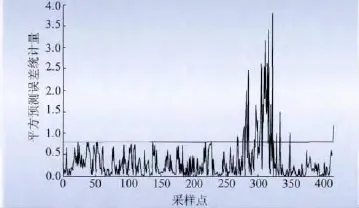
图7 RPCA 的SPE 统计量监控图Fig.7 SPE statistic monitoring chart of RPCA

通过分析SCADA 系统的运行记录，风电机组在316 点，即2011年5月2 日10:51，由于桨距角不对称故障，致使机组停机，故障记录如表1 所示。监测结果与运行故障记录一致。这是由于风电机组变桨系统在出现桨距角不对称故障时，每个叶片的桨距角不同，使3个叶片产生的升力与阻力无法保持一致，继而产生不对称的气动载荷(特别是轴向载荷)，激励塔架，使其振动加剧。而包括齿轮箱在内的传动链系统由于位于具有止推作用的主轴轴承之后，受不平衡载荷影响较小，其振动特性基本保持不变。塔架振动和传动链振动的以上区别导致在图2 中275点后两者呈现相反的变化趋势(见图2 中塔架和传动链振动曲线上椭圆标出的区域)。在此情况下，相关变量集中的塔架振动和传动链振动两个变量之间的关系与机组正常运行时两者变化趋势相同的特性相比发生了显著异常变化。这种变量之间关系的异常变化被本文RPCA 监测方法准确及时捕捉到。采用本文的基于RPCA 的塔架振动建模和监测方法能够及时准确地发现如上述桨距角不对称故障(从275 点超过阈值至316 点故障导致停机，提前约7 h 发现桨距角不对称故障)，避免机组长时间运行在严重影响其健康和寿命的载荷不对称状态。

表1 故障数据Tab.1 Failure data

4 结 论

风电机组SCADA 系统中记录的运行数据能够真实地反映机组部件的运行状态。本文采用风电机组实际运行数据，结合其运行原理，详细分析了塔架振动的主要影响变量。进而采用相对主元分析方法建立了额定风速以下的塔架振动模型，该模型揭示了塔架振动的重要激励源之一为叶轮气动特性，因此叶轮运行异常会导致塔架振动的异常变化，并能够被相对主元塔架振动模型及时监测出来。本文以叶轮的桨距角不对称故障为例，验证了塔架振动监测的有效性。

［1］Hameed Z，Hong Y S，Cho Y M，et al． Condition monitoring and fault detection of wind turbines and related algorithms:a review［J］． Renewable and Sustainable Energy Reviews，2009，13(1):1-39．

［2］张照煌，丁显，刘曼，等． 基于小波变换的风电机组传动系统故障与分析［J］． 应用基础与工程材料学报，2011，19(s):210-218．

［3］Yang W X ，Richard C ，Tavner P J． Bivariate empirical mode decomposition and its contribution to wind turbine condition monitoring［J］． Journal of Sound and Vibration，2011，330:3766-3782．

［4］贺德馨．风工程与工业空气动力学［M］． 北京:国防工业出版社，2006:124．

［5］朱鑫鑫，邵立峰． 基于PC104 的风电机组在线振动状态监测系统［J］． 自动化应用，2013(10):48-49．

［6］梁瑞庆，王浩，王炽欣． 风电机组塔架桩基础的基桩竖向力计算方法［J］． 电力建设，2010，32(6):80-83．

［7］傅质馨，赵敏，袁越，等． 基于无线传感网络的海上风电机组状态监测系统构建方法［J］． 电力系统自动化，2014(7):23-28．

［8］姚兴佳，刘颖明，刘光德，等． 大型风电机组振动分析和在线状态监测技术［J］． 沈阳工业大学学报，2007，29(6):627-632．

［9］郭鹏，Infield D，杨锡运． 风电机组齿轮箱温度趋势状态监测及分析方法［J］． 中国电机工程学报，2011，31(32):129-136．

［10］郭鹏，徐明，白楠，等． 基于SCADA 运行数据的风电机组塔架振动建模与监测［J］． 中国电机工程学报，2013，33(5):128-136．

［11］文成林，胡静，王天真，等．相对主元分析及其在数据压缩和故障诊断中的应用研究［J］．自动化学报，2008，34(9):1128-1139．

［12］王天真，汤天浩，文成林． 相对主元分析方法及其在故障检测中的应用［J］． 系统仿真学报，2007，19(13):2889-2894．

［13］胡静，刘荣利，文成林． 基于相对主元分析的故障检测与诊断方法［J］．弹箭与制导学报，2007，27(3):329-331．

［14］王海清，宋执环，王慧． PCA 过程监测方法的故障检测行为分析［J］． 化工学报，2002，53(3):297-301．

［15］李想．基于主元分析的工业过程故障诊断算法研究［D］． 沈阳:沈阳大学，2010．