风力发电机组旋转Fourier 谱物理机制

贺广零，佟 辉

(1．中国电力工程顾问集团华北电力设计院工程有限公司，北京市100120;2．大庆油田电力集团宏伟热电厂，黑龙江省大庆市163411)

0 引 言

基于常规的紊流风速功率谱(如Von Karman 谱，Kaimal 谱，Davenport 谱等)很难准确预测风力发电机组的疲劳荷载，实际的疲劳荷载往往远比预测值大。此外，也无法成功建立实测风速和风力发电机组动力响应(尤其是塔筒基底弯矩)之间的联系。现场实测表明，旋转叶片上的紊流风谱与固定点的紊流风谱大相径庭，其能量分布发生了根本变化。总体上，是由于叶片旋转效应导致作用在叶片上的风场结构发生变化所致。因此，为准确描述作用在旋转叶片上的风荷载，必须考虑叶片旋转效应。1955年，Rosenbrock［1］最早提出了考虑叶片旋转效应的紊流风速模型。半个世纪以来，考虑叶片旋转效应的紊流风速模型主要有:PNL 模型和SNL 模型。

为了能够描述作用在旋转叶片上的风速，Connell［2-3］将欧拉坐标系转换到旋转坐标系，并在该坐标系下建立了一种风速功率谱数学模型，即PNL模型。之后，Powell ＆ Connell［4-7］、Connell［8］对PNL模型进行了持续完善，并推广应用。然而，PNL 模型自身存在如下缺陷:(1)仅能模拟叶片上一点的风速，无法考虑风轮平面上不同点之间的相关性;(2)未能考虑叶片数量的影响;(3)需要源谱在进行Fourier 变换后能获得解析表达式，要求过于苛刻。

与此同时，Veers［9-10］对风轮平面上各取样点进行风场模拟以获取风速时程，然后随着叶片旋转移动逐点提取瞬时风速，所提取的瞬时风速依序构成一组新的风速时程。与PNL 模型相比，SNL 模型简单、直观，能对整个风场进行有效模拟，且对源谱和相干函数没有特殊要求，故而更具开放性。然而，该模型同样存在一些弊端:(1)只是在风速层次上考虑了叶片旋转效应，并未真正构建旋转样本谱;(2)进行风场模拟时，相位信息不太容易精确控制，容易导致较大的误差;(3)叶片上点暂时不经过的位置也会进行风场模拟，计算效率较低。PNL 模型和SNL 模型具有共同的本质，是从不同角度来诠释叶片的旋转效应。简单来说，PNL 模型是从Lagrange 描述的角度研究叶片旋转效应，而SNL 模型则立足于Euler 描述。有关叶片旋转效应，尽管已有学者进行了较长时间的探索，但其物理机制并非如人们所期望的那样清晰，其物理意义及工程价值还有待进一步探索。

本文从一个新的角度来探索叶片旋转效应的物理机制，推导基于物理机制的叶片旋转Fourier 谱。在推导过程中，摈弃平稳过程概念和各态历经假定，反映真实动力过程的特征。进一步地，在完成旋转Fourier 谱参数分析的基础上，明确其物理意义。

1 旋转Fourier 谱的物理机制

近年来，相当一部分学者认为［11-12］:风场中大部分漩涡尺寸要小于叶片尺寸，当该漩涡经过叶轮平面时，叶片将切割漩涡若干次，即所谓的"漩涡切割"现象(图1)。换句话说，相对固定点的风速而言，旋转叶片上的风速经历了紊流风场的空间结构变化。因为叶片切割漩涡若干次，叶片将经历相应次数紊流风场结构的变化，从而导致紊流风谱出现能量重分布。显然，这种对叶片旋转效应物理机制的阐述晦涩难懂，且难以用数学公式来衡量。

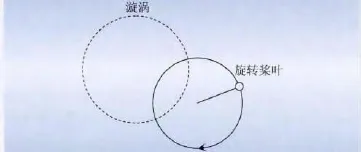
图1 漩涡切割现象Fig．1 Eddy slicing phenomenon

为拨开叶片旋转效应的重重迷雾，笔者将从另一角度探索其物理机制。一般来说，紊流风场是一个时变随机场，即空间中任意一点的紊流风速不仅与该点的空间位置有关，而且还与时间有关。此外，风力发电机组紊流风场还具有其特殊性:叶片上任意一点的空间位置随着叶片旋转而不断变化，从而使得紊流风场空间变化性更为复杂。为了能较好地刻画作用在旋转叶片上的风速时程，首先需要转换思考角度，将坐标系切换至旋转坐标系。为了能跟踪旋转叶片的轨迹，可有规律地沿着旋转叶片的轨迹选取样本点(图2)。在旋转叶片经过某样本点时，提取该样本点风速时程在该时刻的瞬时风速，依此类推，将提取的瞬时风速按既有的时间顺序排列可构建一组新的风速时程。显然，这组风速时程的共同特征在于:自始至终作用于旋转叶片上某一点，而这组风速时程对应的紊流风速谱模型即为旋转Fourier 谱。

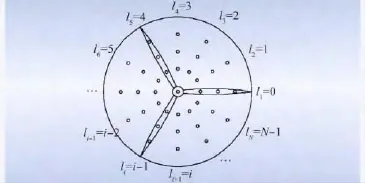
图2 风轮平面上取样点位置Fig．2 Sampling location on rotor plane

2 样本互相关函数与Fourier 互谱

在旋转Fourier 谱物理过程分析中，需要获得样本互相关函数与Fourier 互谱之间的关系。在此，首先对二者之间的关系进行推导。值得说明的是，以下推导均基于有限时长的样本时程，摈弃了平稳过程概念和各态历经假定，反映了真实动力过程的特征。

对于2个不同的样本时程x1(t)、x2(t + τ)，其Fourier 变换可分别定义为

其相应的样本Fourier 密度谱可分别定义为

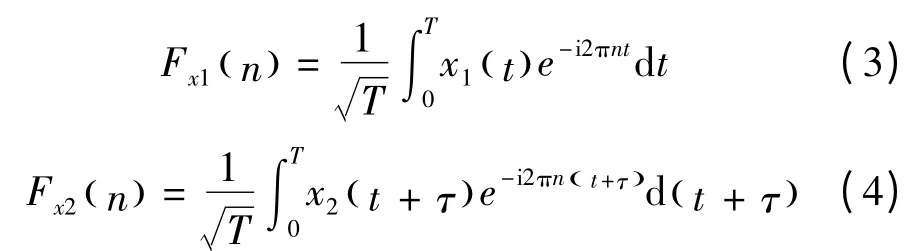
同时，时程x1(t)、x2( )t 的样本互相关函数可定义为

利用式(1)、(2)，可得

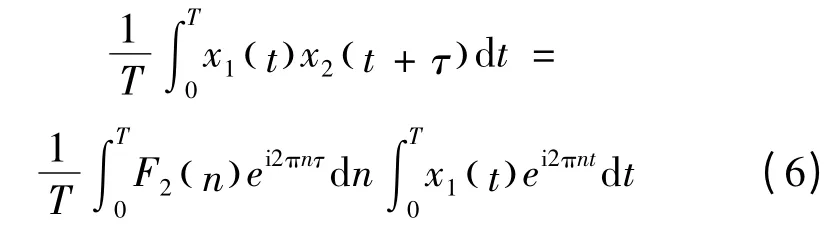
故

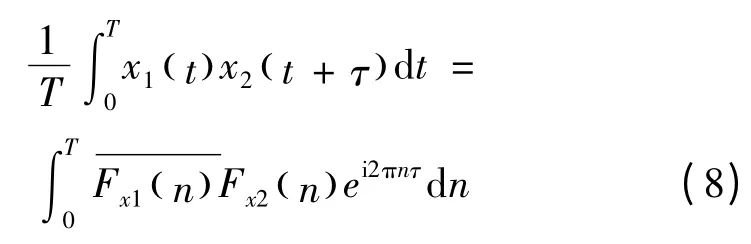
即

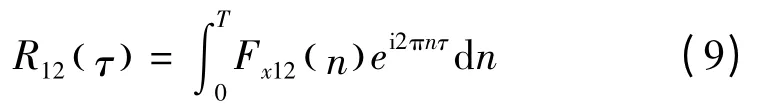
同理可得

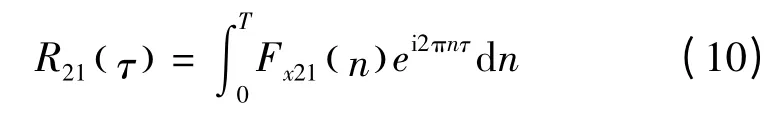
显然，Fourier 互谱Fx12(n)可以表示为

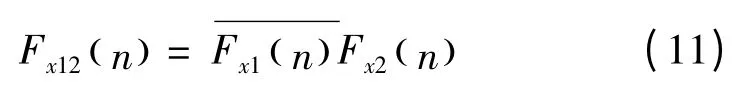
在另一方面，引入相干函数概念，Fourier 互谱也可以表示为

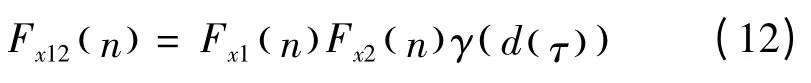
显然，相干函数(γ d(τ))为

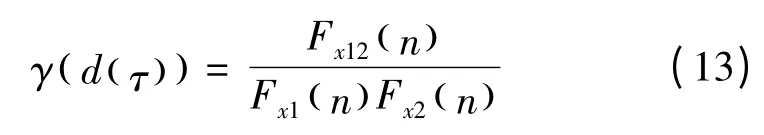
一般情况下，(γ d(τ)) 取决于两点之间的距离d(τ)。

依据式(12)，式(13)可以改写为

由上式可知，样本互相关函数与Fourier 互谱构成Fourier 变换对。

样本时程x(t)自相关函数R11(τ) 可定义为

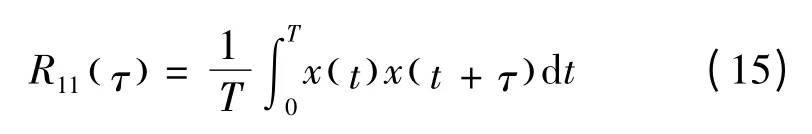
依据(8)式，当x1(t) = x2(t)时可得

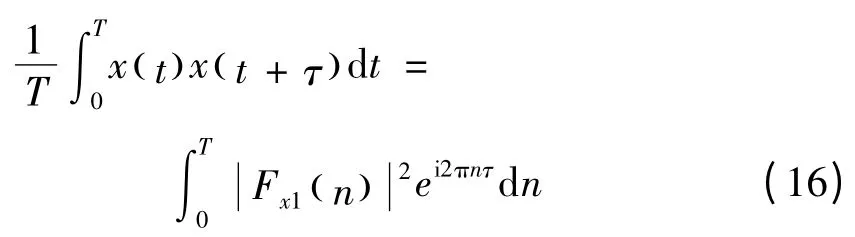
即

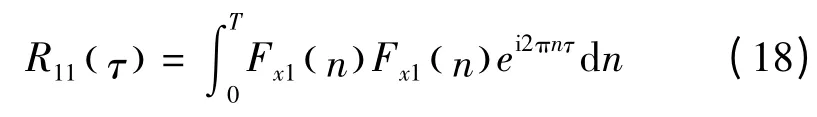
由上式可知，样本自相关函数与Fourier 自谱构成Fourier 变换对。

3 旋转Fourier 互谱

由旋转Fourier 谱的物理机制可知，旋转Fourier互谱与经典的紊流风谱互谱存在本质的不同，已然不再是自谱与相干函数的简单乘积。已知叶片以转速n0匀速旋转，半径ri上的一点在t 时刻的风速时程样本为xi，半径rj上的一点在t + τ 时刻的风速时程样本为xj(图3)。d(τ)为两点间距离(图3)，其表达式为

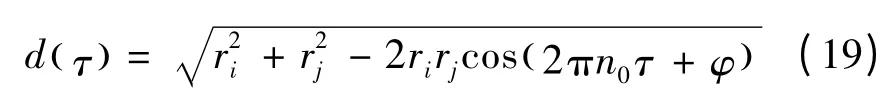
式中φ 为相位因子。当i、j 两点处于同一片叶片上时，φ = 0 ;当i、j 两点处于不同叶片上时，φ 则为2π/Nb(Nb为叶片数目)的整数倍。对于三叶片风力发电机而言，φ 始终维持为2π/3 。

由(14)式可知，Fourier 互谱与互相关函数构成Fourier 变换对。对Fourier 互谱［13］进行逆Fourier 变换，可得两点间的互相关函数为

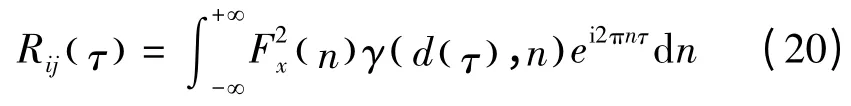
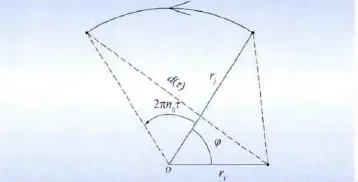
图3 旋转叶片相对位置关系Fig．3 Relative position of rotational blade

根据旋转Fourier 谱的物理机制，旋转叶片上任意两点在不同时刻的相关函数可用两点间的互相关函数来代替，即

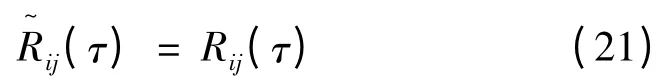
值得注意的是，Rij(τ)为i 点与转动时间τ 后j点的互相关函数。对互旋转相关函数进行Fourier 变换可得到旋转Fourier 互谱ij(n)为

将式(20)、(21)代入式(22)中

与前述分析类似，将γ(d(τ)，n')进行Fourier 级数展开

式中:n0为叶片转动频率;k'm(n)为相干函数γ(d(τ)，n)的Fourier 展开系数。

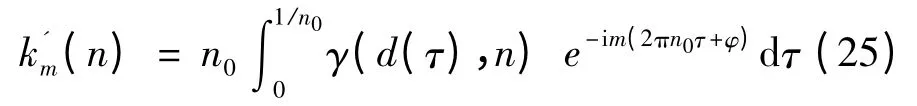
将(24)式代入(25)式中，有

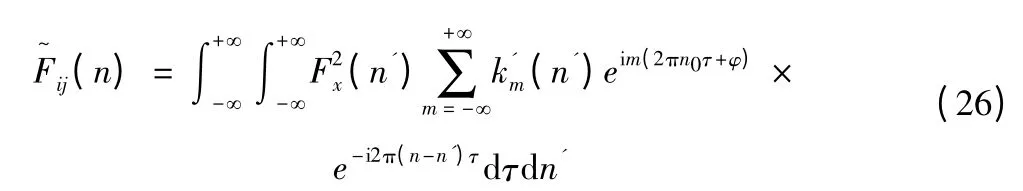
亦即

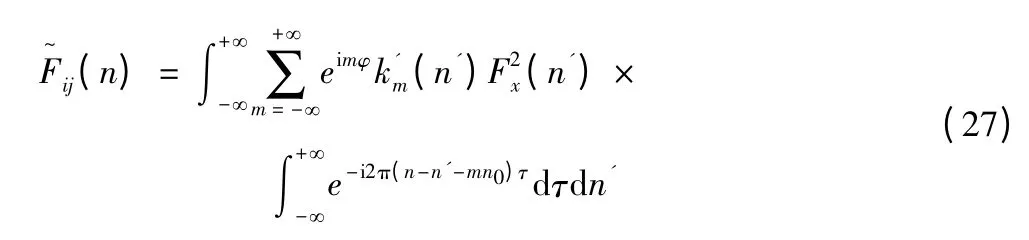
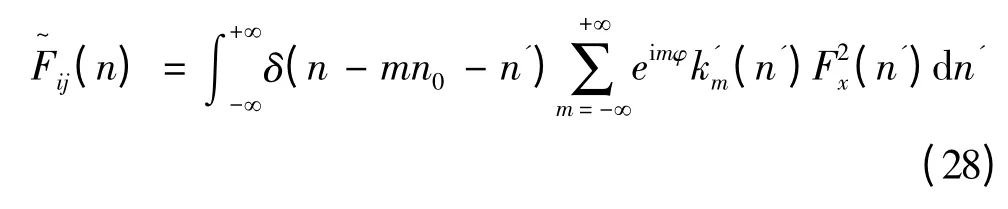
进而可得

式中，k'm(n － mn0)为旋转模态，本质上为相干函数的Fourier 展开系数。eimφ为叶片标识项，当φ = 0 时，为同一片叶片上的互谱;当φ ≠0 ，为不同叶片上的互谱。令ri= rj且相位因子φ = 0 ，可得旋转Fourier自谱ii(n)为

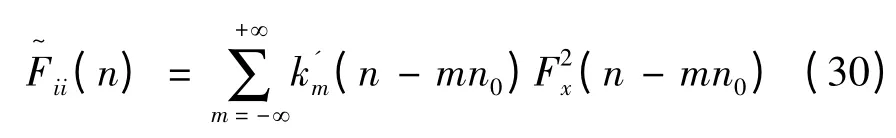
4 旋转Fourier 谱参数分析

以典型的1.25 MW 三叶片变桨距风力发电机组为例进行分析。依据风机厂家提供的资料，该机型主要参数如下:叶轮直径为64 m，转速为30 r/min(0.5 Hz)，轮毂高度为68 m，10 m 高处平均风速为15 m/s，地面粗糙度为0.02 m，湍流积分长度73.5 m。

图4 给出了旋转Fourier 谱与样本Fourier 谱之间的比较。由图4 可知，旋转Fourier 谱出现能量重分布:由低频向高频大幅度转移，并在旋转频率n0的整数倍处出现峰值。由式(29)可知，旋转Fourier 谱ij(n)是由无限个样本Fourier 谱Fii(n)叠加而成，而这些样本Fourier 谱在叠加之前先进行了叶片旋转频率n0整数倍平移。如此，旋转Fourier 谱能量重分布的本质一目了然。

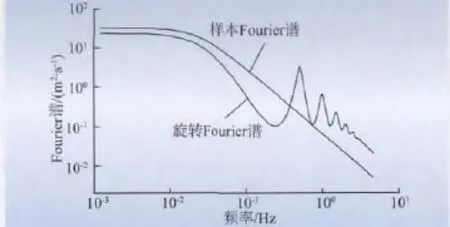
图4 旋转Fourier 谱与样本Fourier 谱比较Fig．4 Comparison between rotational ＆sampling Fourier spectrum

不难判断，旋转Fourier 谱与计算点半径、叶片旋转频率密切相关。同时，旋转Fourier 谱以随机Fourier 谱为源谱［14］，自然相应地以10 m 高平均风速、地面粗糙度为主要影响因素。以下将针对各影响因素逐个进行参数分析。

(1)计算半径的影响。图5 分别给出了计算半径为30，20，10，0 m 时的旋转Fourier 谱曲线。由图5不难发现:计算点半径r 对旋转Fourier 谱的影响:当r =30 m 时，旋转效应最为显著，能量重分布最为突出;r =20 m、r =10 m 旋转效应依次减弱;r =0 m 时，叶片旋转效应彻底消失。总体上，随着计算半径的递减，叶片旋转效应逐渐减弱。

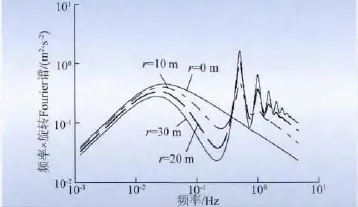
图5 计算点半径对旋转Fourier 谱的影响Fig．5 Influence of computing radius on rotational Fourier spectrum

(2)旋转频率的影响。图6 展现了叶片旋转频率n0对旋转Fourier 谱的影响。对于大型风力发电机组而言，叶片旋转频率范围大致为0.2 ～0.6 Hz，不妨取0.2，0.4，0.6 Hz 为代表进行分析。旋转Fourier 谱对旋转频率高度敏感，旋转频率的些许变化就会引起旋转Fourier 谱曲线较大的调整，主要体现在以下2个方面:1)随着旋转频率的增加，旋转Fourier 谱峰值快速增大，谷值快速减少，叶片旋转效应趋于显著;2)旋转Fourier 谱的峰值出现在叶片旋转频率的整数倍处。因此，随着旋转频率的增加，旋转Fourier 谱峰值整体向右平移。值得指出的是，三者在低频阶段基本重合，只是在高频阶段开始分化。

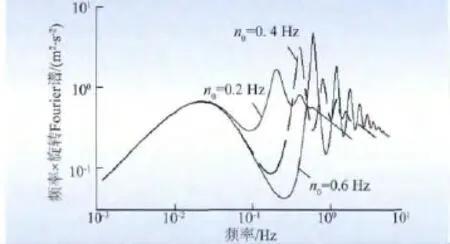
图6 旋转频率对旋转Fourier 谱的影响Fig．6 Influence of rotational frequency on rotational Fourier spectrum

(3)平均风速的影响。图7 展示了轮毂高度处平均风速对vh旋转Fourier 谱的影响。一般地，风力发电工程以10 m 高度处平均风速为代表，而风电项目则习惯以轮毂高度处平均风速为代表，二者存在一定的换算关系。该风力发电机组的切入风速、切出风速分别为4、25 m/s，因此在二者中间选择了3个代表性风速(8、16、24 m/s)进行分析。为了获得比较明显的计算结果，选定计算点距轮毂中心30 m。不难发现，当轮毂高度处平均风速较小时，旋转Fourier谱峰值较大，谱谷值较小，谱曲线形状细长、尖锐。随着平均风速的逐渐增大，旋转Fourier 谱峰值减少，谱谷值增大，谱曲线形状趋于平缓、丰满。此外，在低频阶段，三者峰值对应的频率存在一定差异。

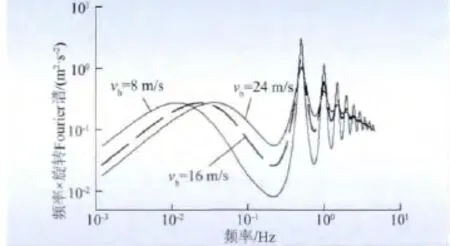
图7 平均风速对旋转Fourier 谱的影响Fig．7 Influence of mean wind speed on rotational Fourier spectrum

(4)地面粗糙度的影响。图8 体现了地面粗糙度z0对旋转Fourier 谱的影响。地面粗糙度z0与地形地貌紧密相关。在分析过程中，赋予z0= 0． 005，0.07，0.3，1.0，分别对应于海岸区、开阔地形、郊区地形、城市中心四种地形。由图8 可知，随着地面粗糙度z0增大，旋转Fourier 谱值整体向上平移。其原因在于增大地面粗糙度z0会使得剪切流动速度变大，进而导致脉动风标准差增大，最终引起旋转Fourier 谱能量增加，在图形上则表现为谱值向上平移。

(5)自谱与互谱的比较。图9 为旋转Fourier 互谱与自谱的比较。以不同半径r1=30 m 和r2=20 m上的2 点之间的互谱为例，同时与r1= r2=30 m，r1=r2=20 m的自谱进行比较。互谱的形状与自谱的形状大体相似。在低频段，互谱值介于2个自谱值之间;而在高频段，互谱值衰减非常迅速，以至于远小于2个自谱值。

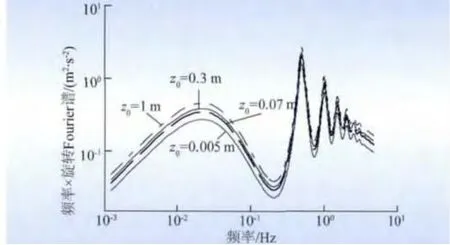
图8 地面粗糙度对旋转Fourier 谱的影响Fig．8 Influence of surface roughness on rotational Fourier spectrum

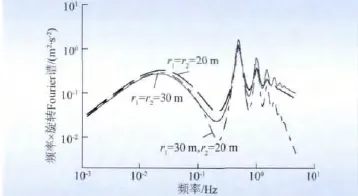
图9 旋转Fourier 互谱与自谱的比较Fig．9 Comparison between cross ＆auto rotational Fourier spectrum

5 旋转Fourier 谱的物理意义与工程价值

(1)旋转Fourier 谱以随机Fourier 谱为源谱，而随机Fourier 谱本质上为物理随机函数模型。物理随机函数模型可以有效地避免经典现象学随机过程模型的种种局限性［15］，不仅可以给出风电机组随机风场的完整数学描述，而且由于其具备明确的物理意义，使得对于风电机组随机风场的实验验证成为可能，同时也有助于发现随机性的客观来源。

(2)PNL 模型和SNL 模型都是从时域角度来分析叶片旋转效应，本文则从频域的角度出发，建立了旋转Fourier 谱物理模型。这不仅是思考角度的变化，更重要的是建立了旋转Fourier 谱与其源谱之间的映射关系，这意味着旋转Fourier 谱的源谱可以是任意一种合理的紊流风谱。同时，由于以随机Fourier 谱为源谱，且该谱本质上为随机函数，具有明确的物理机制，是迄今为止最为合理的紊流风速谱。当然，旋转谱的源谱也可以是经典功率谱，如Karman谱、Kaimal 谱、Simiu 谱等，功率谱对应的旋转谱可定义为旋转样本谱［16］。同时，若将来出现的更为合理的风速谱，则可直接纳入本文提出的映射机制获得更为精确的旋转谱。因此，本文提出的旋转谱不仅简单、明确，而且具有很强的兼容性和普适性。

(3)旋转Fourier 谱反映了风速作用在旋转叶片上的物理机制，其本质上为作用在旋转叶片上紊流风速时程对应的随机Fourier 谱。旋转Fourier 谱反映了作用在旋转叶片上风速的时间、空间双重变化，不仅体现了风速自身的脉动特性(时变特性)，而且刻画了叶片高度周期性变化引起的脉动风速调整(空间变化特性)。因此，旋转Fourier 谱能更准确地预测风力发电机组极值荷载，尤其是疲劳荷载。

(4)旋转Fourier 谱的突出优势是:在保证分析结果可靠的前提下，能将叶片旋转这一个运动学问题简化为静力学问题［13，17-18］。如何考虑叶片旋转效应是风力发电机组风致随机动力响应分析的核心问题。事实上，基于有限元法建模无法模拟叶片旋转(刚体运动)。运动具有相对性，以旋转叶片为参照物，视叶片风场在不停地反方向旋转，基于这种思想构建旋转Fourier 谱，显然已经有效地考虑了叶片旋转效应。因此，基于该谱进行风力发电机组风致动力响应分析时无须再次考虑该效应，这对风力发电机组结构分析而言，无疑是个很大的简化。

6 结 论

基于风速作用于旋转叶片的物理机制，对相干函数进行Fourier 级数展开，利用δ 函数的性质，推导了旋转Fourier 自谱和互谱表达式。研究表明，旋转Fourier 谱会出现能量重分布现象，且与计算半径、叶片旋转频率、平均风速、地面粗糙度等因素密切相关。采用旋转Fourier 谱，能够更准确地预测风力发电机组极值荷载，尤其是疲劳荷载;在保证分析结果可靠的前提下，能将叶片旋转这一个运动学问题简化为静力学问题。

［1］Rosenbrock H H． Vibration and stability problem in large turbines having hinged blades［D］． E．R．A．，Surrey，U．K．，1955．

［2］Connell J R． Turbulence Spectrum observed by a fast-rotating wind turbine blade ［R］． Technical Report PNL-3426，Batelle Pacific Northwest Laboratory，Richland，WA，1980．

［3］Connell J R． The spectrum of wind speed fluctuations encountered by a rotating blade of a wind energy conversion system ［R］．Technical Report PNL-4083，Batelle Pacific Northwest Laboratory，Richland，WA，1982．

［4］Powell D C，Connell J R，George R L． Verification of theoretically computed spectra for a point rotating in a vertical plane［R］．Technical Report PNL-5440，Battelle Pacific Northwest Laboratory，Richland，WA，1985．

［5］Powell D C，Connell J R． A model for simulation rotational data for wind turbine applications［R］． Technical Report PNL-5857，Battelle Pacific Northwest Laboratory，Richland，WA，1986．

［6］Powell D C，Connell J R． Review of wind simulation methods for horizontal-axis wind turbine analysis［R］． Technical Report PNL-5903，Battelle Pacific Northwest Laboratory，Richland，WA，1986．

［7］Powell D C，Connell J R． Verification of theoretically computed spectra for a point rotating in a vertical plane［J］． Solar Energy，1987，39(1):53-63．

［8］Connell J R． A primer of turbulence at the wind turbine rotor［J］．Solar Energy，1988，41(3):281-293．

［9］Veers P S． Modeling stochastic wind loads on vertical-axis turbines［R］． Technical Report SAND83-1909， Sandia National Laboratories，A1buquerque，New Mexico，1984．

［10］Veers P S． Three-dimensional wind simulation［R］． Technical Report SAND88 -0152， Sandia National Laboratories，A1buquerque，New Mexico，1988．

［11］Salzmann D J C． Dynamic response calculation of offshore wind turbine monopile support structures ［D］． Delft University of Technology，Netherlands，2004．

［12］Tempel J V D． Design of support structures for offshore wind turbines［D］． Delft University of Technology，Netherlands，2006．

［13］贺广零，李杰．风力发电机组风致动力响应分析［J］． 电力建设，2011，32(10):1-9．

［14］贺广零，李杰．基于物理机制的风力发电高塔系统风场模拟［J］．同济大学学报:自然科学报，2010，38(7):976-981．

［15］Li J，Chen J B． Stochastic dynamics of structures ［M］． John Wiley ＆Sons，2009:11-32．

［16］贺广零，李杰． 风力发电高塔系统基于物理机制的旋转样本功率谱研究［J］． 中国电机工程学报，2009，29(26):85-91．

［17］贺广零，李杰． 风力发电高塔系统风致随机动力响应分析［J］．振动工程学报，2011，26(4):696-703．

［18］贺广零，李杰． 风力发电高塔系统抗风动力可靠度分析［J］． 同济大学学报:自然科学报，2011，39(4):474-481．