架空线路用货运索道承载索数值模拟分析
钮永华,王志华,夏顺俊
(江苏省送变电公司,南京市211102)
0 引 言
随着特高压电网的大面积开工建设,长距离跨区输电线路路径的地形地势、地貌特征复杂多变[1-2]。特高压架空输电线路在进行基础、组塔、架线等工序施工时,所需运输的材料、设备、工器具等,其形体尺寸和质量均较一般架空输电线路更为庞大。当施工区域在高山大岭地区时,若采用车辆或人力畜力运输,必将采取开山放炮、伐木毁林、填土铺路等措施以开辟运输通道。当采取上述措施时,不仅大大增加了运输成本,而且由于破坏环境所造成的损失也大大增加。特别是在山区无运输道路的条件下,当所运输的物件形体尺寸和质量超过一定限度时,人力或畜力就无法运输,如特高压架空输电线路钢管塔的大型钢管及座地式抱杆的大型部件等。若采用直升飞机空运,目前国内成熟的案例并不多见,且运输成本也比地面运输增加很多。因此,目前国内特高压架空输电线路在山区无运输道路条件下的工地运输,越来越普遍地采用架空输电线路施工专用货运索道。专用货运索道运输方式经济合理、适用范围广阔、可显著地提高施工效率、减少环境破坏及节约人力成本[3]。
架空输电线路施工专用货运索道由工作索(承载索、返空索和牵引索)、支架、行走机构(承载索和返空索鞍座、行走小车和挂钩等)、牵引装置及起始端锚固系统(含锚板、拉棒或钢丝绳、卸扣、调整用链条葫芦、测力装置等)等部分组成。架空输电线路施工专用货运索道的各组成部分中,工作索的受力计算是专用索道施工计算中的核心部分,工作索中承载索设计计算的精度直接影响专用货运索道在使用过程中的安全性及经济合理性[4]。承载索的受力计算结果不仅是承载索选型及施工现场定位的基础,而且直接影响支架的受力和起始端锚固系统的受力,承载索的受力计算也是支架和起始端锚固系统设计和选型的基础。
当承载索的跨距足够大时,可视之为像链条一样的柔软而无刚性的悬链[5],并以此来建立承载索的悬链线方程。本文将承载索简化为多跨的悬链线方程组,建立计算模型,直观快速地解算承载索的各关键数值。
1 建立承载索计算模型
架空输电线路施工专用货运索道承载索的两端在地面锚固,中间选择合适的位置用支架撑高,由压覆在承载索上的行走小车承担货物的荷重。承载索空载及荷载时的断面简图如图1 所示。
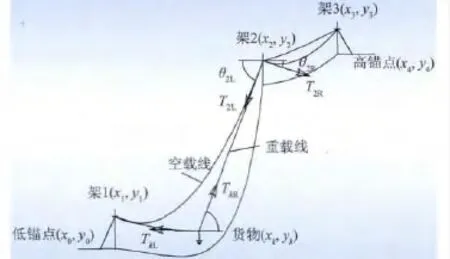
图1 承载索空载及荷重时的断面简图Fig.1 Section diagram of load cable with load and non-load
1.1 确定承载索断面坐标
架空输电线路施工专用货运索道路径确定后,承载索的高低锚固点,必要的中间支撑点均初步选定。以承载索低端锚固点的断面坐标值为(0,0),实测高端锚固点的坐标值为(xn,yn),并实测各支撑点的坐标值及地表线关键点的坐标值(xi,yi)。按照所测断面各点的坐标值,承载索各跨的档距及高差分别为
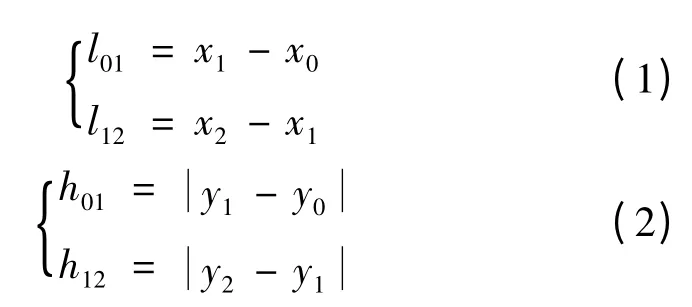
式中:li(i+1)为水平档距,m;hi(i+1)为悬点高差,m。
1.2 承载索初始张力及承载索空载线长计算
承载索的初始张力可根据经验初步设定,一般设承载索低端锚点处初始张力为T(0)0,则低端锚点至架1 档内的悬链线公式为
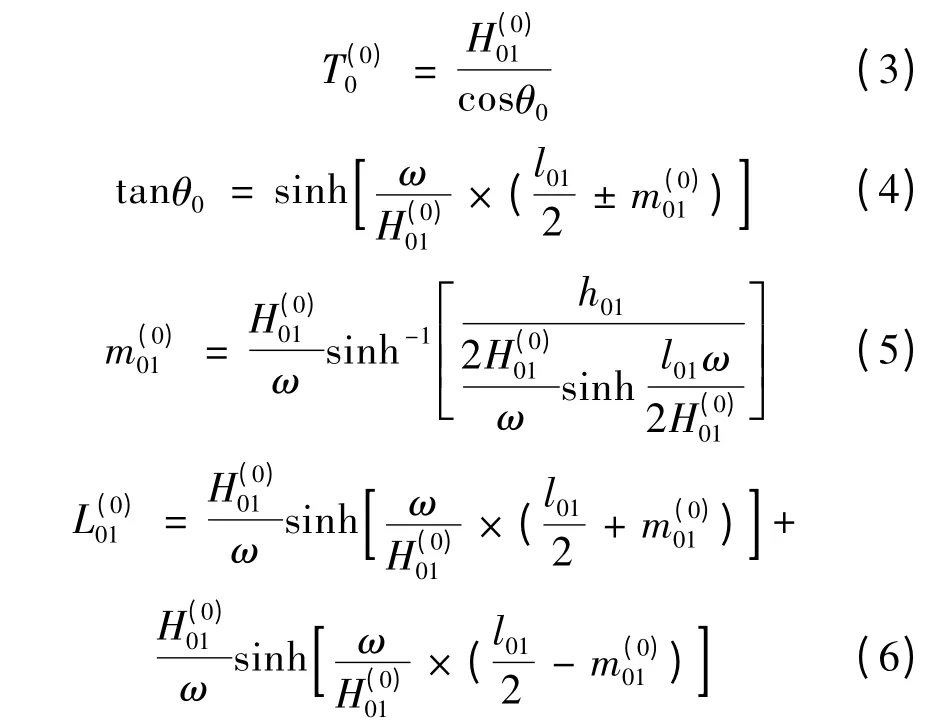
承载索在架1 处左侧张力的计算公式如下:

式中:θ1L为承载索在架1 处左侧切线对水平线夹角,(°)。
承载索支点为鞍座结构,材质为钢,承载索是涂油的钢丝绳,鞍座在加工时均考虑过承载索钢丝绳需在其内部滑移,一般均要求其摩阻系数小于0.02。承载索在支点处的滑动摩擦力等于正压力乘以摩阻系数,支点处的正压力远小于承载索的张力,因此承载索因支点处摩擦而增加的张力小于承载索总张力的1%。为简化计算,可假定架1 处承载索支点摩阻系数为0(其余支点处摩阻系数也假定为0),承载索右侧张力等于左侧张力,即。由架1 右侧的张力可计算架1 和架2 档内水平张力及架2 的左侧张力。通过逐档推进演算,空载时承力索的所有张力线长均可进行计算。
任意档内的悬链线计算公式如下:
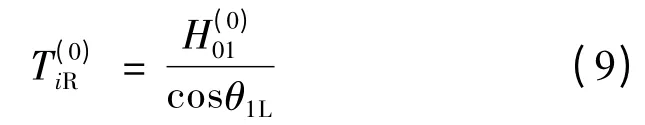
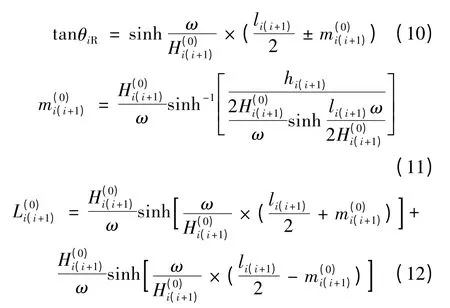
因此,承载索在空载状态下,若中间有n个支架,则承载索将被分割为n +1个档距,可以建立n +1个悬链线方程,所有方程中可将各档水平张力视为自变量,其余各点的张力、高程及线长均为应变量。
上述n +1 悬链线方程组可以利用Excel 中的规划求解工具进行解算。即设各档水平张力为可变单元格(共n + 1个可变单元格),约束条件为(有n个约束条件)及= a(a 为初始设定的张力)。
承载索空载时的总线长计算公式如下:
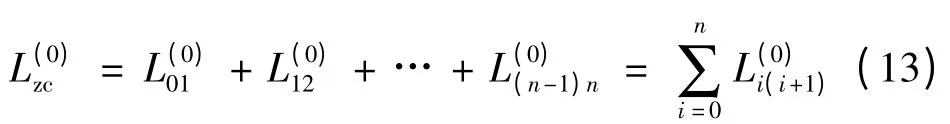
1.3 单个集中荷载时承载索的断面坐标参数
承载索在承载单个最大集中荷载时是最恶劣工况[6],数值模型以此工况进行模拟分析。
设集中荷载的断面坐标为(xk,yk),则集中荷载至左侧最近支架为一悬链线,至右侧最近支架为另一悬链线。集中荷载左侧的水平档距lik= xk-xi、左侧悬点高差,集中荷载右侧的水平档距lk(i+1)= x(i+1)-xk、右侧悬点高差
1.4 集中荷载处承载索张力的垂直分量计算
集中荷载处承载索左右侧的垂直分量之和与集中荷载的重力相平衡,计算公式如下:
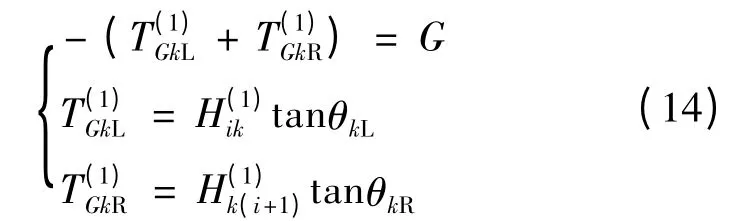
1.5 支架处的垂直下压力计算
任意支架垂直下压力的计算公式如下:

1.6 承载索空载和荷载时线长的平衡方程
承载索由于两端锚固,在荷载时由于张力的增加和温度的改变使其与空载时的总线长相比有变化,计算公式如下:
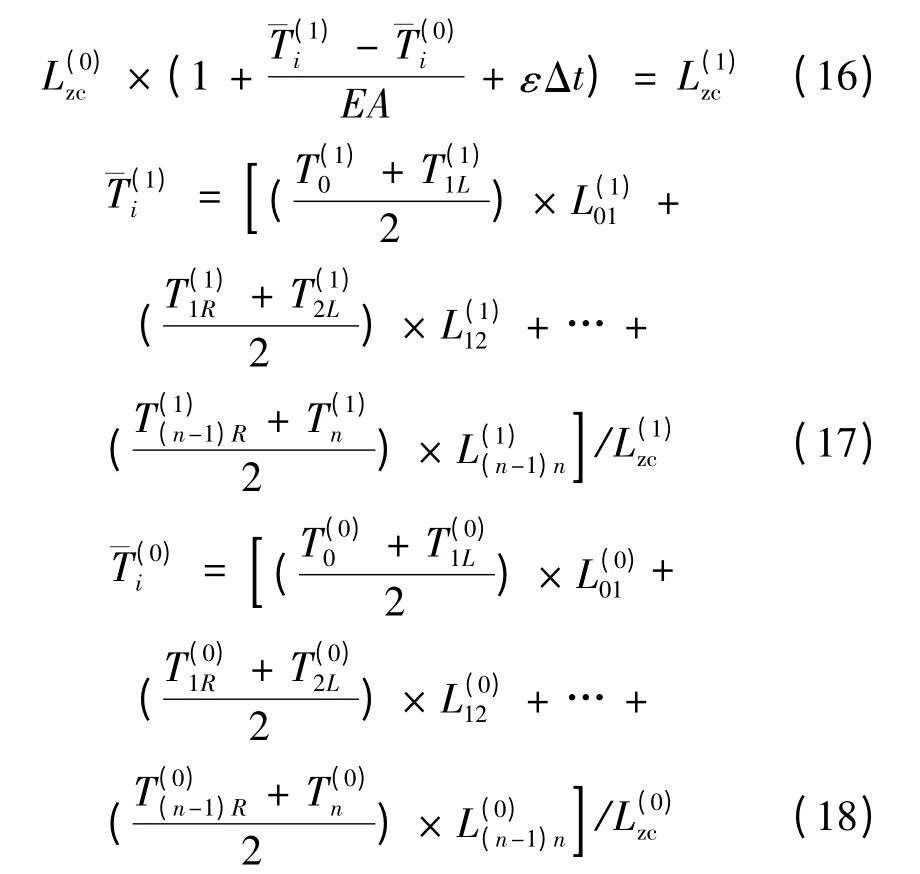
1.7 承载索空载和荷载时平衡方程的求解
承载索在单个集中荷载时,中间有n个支架,则承载索将被分割为n +2个档距,可以建立n +2个悬链线方程,所有方程中可将各档水平张力和荷载处纵坐标yk视为自变量,其余各点的张力、高程及线长均为应变量。
上述n +2 悬链线方程组可以利用Excel 中的规划求解工具进行解算。即设各档水平张力和荷载处纵坐标yk为可变单元格(共n + 3个可变单元格),约束条件为有n +1个约束条件)、= G(中荷载重力平衡)(空载和荷载时线长平衡)。
当集中荷载的个数增加时,可变单元格和约束条件也增加[7-9],仍可用Excel 中的规划求解工具进行解算。
1.8 承载索荷载时在障碍点处的标高yZA 解算
当荷载位于障碍点所在的档内时,若障碍点处的横坐标为xZA,则障碍点处承载索的标高yZA按此处的悬链线方程进行解算,公式如下:
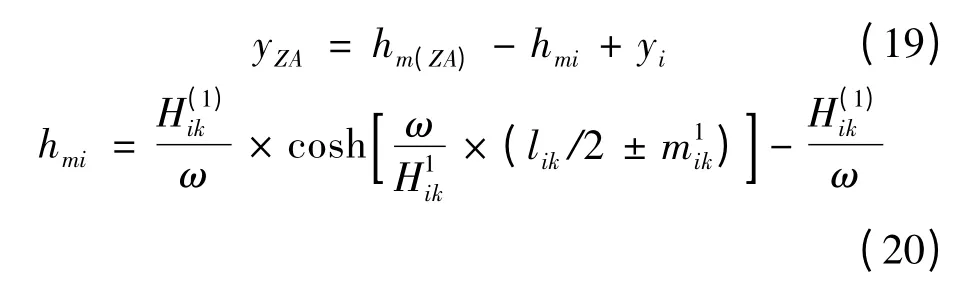
悬链线最低点在档内时,hm(ZA)按式(21)计算:
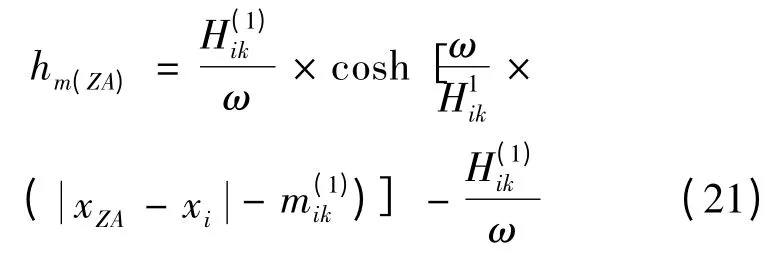
悬链线最低点在档外时,hm(ZA)按式(22)计算:
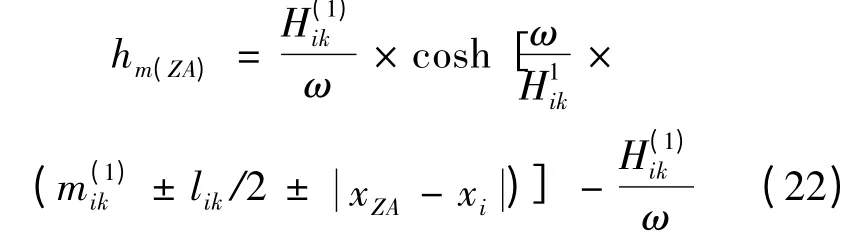
式中:hmi为悬链线最低点至支架点i 的高差,m;hm(ZA)为悬链线最低点至障碍点i 的高差,m。
当承载索上的荷载点位于障碍点处时,障碍点处的标高yZA为最小值,该处的标高值需大于障碍点处的地面标高加安全高度要求。若此处的标高不能满足要求,则需调整承载索空载的初始张力,直至符合要求[10]。
上述承载索计算模型适用承载索的刚度影响极小,承载索形状符合悬链线线型,承载索受力变形在线弹性变形范围以内,也即承载索的最小跨距大于10 m,最大跨越小于1 000 m 范围以内[11-14]。
2 实例计算及其与实测的比较
1 000 kV 浙福线8 标段4040 号塔位,架设重型往复式双承载索架空输电线路施工专用货运索道,支架为6 柱式钢管“A”字架结构,支架横梁为双拼工字钢结构,额定荷载为300 kN;行走机构为50 kN 级双索小车;起始端锚固系统为单索2 ×150 kN 级;牵引机为80 kN索道专用牵引机;牵引索为φ16 mm、6 ×19 结构、油麻芯、公称抗拉强度1 870 MPa、最小破断拉力为158 kN的钢丝绳。承载索使用规格φ28 mm、6 ×19 结构、油麻芯、公称抗拉强度1 870 MPa、最小破断拉力为484 kN的钢丝绳。承载索米重ω=26.87 N/m、钢丝总截面A =289.85 mm2、弹性模量E=100 GPa、线性膨胀系数ε=11.5 ×10-6/℃。索道断面参数为:低端锚点(0,0)、架1(15,3.5)、架2(424,120.5)、架3(447,123.5)、高锚点(462,120)、障碍点(215,35.4)。单根承载索最大集中荷载G =24.517 kN。
2.1 最大集中荷载在障碍点处的计算
将上述参数代入计算模型,按障碍点标高进行控制,并于2013年9月15 日在现场实际测量,所得结果见表1。
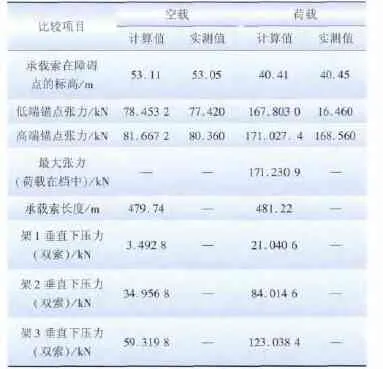
表1 数据测试结果与计算结果对比Tab.1 Contrast of test data and calculation data
2.2 最大集中荷载在最大档(架1 至架2 之间)内移动时的高程和张力变化
将承载索处最大集中荷载在最大档内的横坐标值xk从架1 起,每次增加10 m,计算承载索荷载处的纵坐标值yk。将xk、yk相对应的值通过Excel 的“concatenate”命令转化(xk、yk)数组,在AutoCAD 中利用line 或pline 生成相应的轨迹点,生成的轨迹点如图2 所示。通过比较轨迹点与地面线之间的距离,可直观地看到断面各处的安全高度。

图2 最大集中荷载在最大档内移动的轨迹点Fig.2 Track points of the maximal concentrated load in the longest span
记录障碍点的高程值yZA,转化成坐标数组(xk、yZA)生成障碍点高程曲线如图3 所示,用全站仪实测障碍点处的高程,也在图3 内显示。通过比较障碍点处高程的计算值与实测值,可判断此处高程的变化趋势并验证计算的正确性。
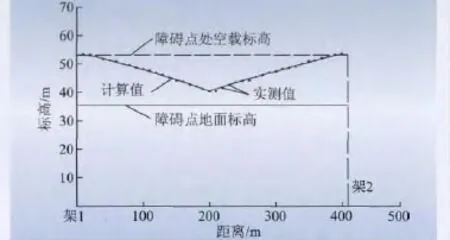
图3 最大集中荷载在最大档内移动时障碍点处的高程变化Fig.3 Elevation change of obstacle when the maximal concentrated load move in the longest span
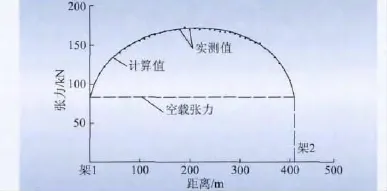
图4 最大集中荷载在最大档内移动时高端锚点的张力变化Fig.4 Tension change of higher anchor point when the maximal concentrated load move in the longest span
通过比较最大集中荷载在最大档内移动时障碍点的高程和高端锚点的张力,实测值与理论计算值的误差均不超过3%,实测的障碍点的高程略大于理论计算值,实测的高端锚点张力略小于理论计算值。
1 000 kV 浙福线8 标段4040 号塔位的架空输电线路施工专用货运索道(重型)已安全运输钢管塔材约2 ×105kg,其余塔位已架设约6 处专用索道(重型),专用索道试运行时所测结果均符合理论计算值。
3 结 论
架空输电线路施工专用货运索道承载索断面坐标和张力问题,可通过建立悬链线方程,以张力平衡、线长平衡和重力平衡为条件,利用Excel 的规划求解工具解算各未知量。并将断面参数和张力参数变换为数组,可简单快速地在AutoCAD 内画出荷载前后的断面和张力变化曲线。该模型计算结果与实测记录相吻合,适用于施工现场的实际应用。
[1]白雪松,缪谦.货运施工索道悬索理论计算模型研究[J]. 电网技术,2008,32(20):90-94.
[2]熊织明,钮永华,邵丽东.500 kV 江阴长江大跨越工程施工关键技术[J].电网技术,2006,30(1):28-34.
[3]白雪松,缪谦,王立军,等.货运施工索道工作索计算软件开发与应用[J].电力建设,2009,30(2):41-44.
[4]单圣涤.工程索道[M].北京:中国林业出版社,2000:75-84.
[5]李博之.高压架空输电线路施工技术手册(架线工程计算部分)[M].北京:中国电力出版社,1989:1-5.
[6]丁宗保,黄成云,朱立明,等.1 000 kV 淮上线特高压钢管塔重型构件索道运输[J].电力建设,2012,33(7):99-101.
[7]郑丽凤. 架空索道悬链线理论研究[D]. 福州:福建农业大学,2002.
[8]靳义奎,陆建荣.多支点循环索道运输在输电线路中的应用[J].青海电力,2009,28(4):41-45.
[9]国家电网公司基建部.国家电网公司输电线路工程货运架空索道运输标准化手册[M].北京:中国电力出版社,2010.
[10]孙竹森,缪谦,江明.输电线路工程货运架空索道标准化施工方案[J].电力建设,2011,32(3):117-120.
[11]Q/GDW 418—2010 输电线路工程货运架空索道运输施工工艺导则[S].北京:国家电网公司,2010.
[12]国网交流工程[2013]237 号. 浙北—福州特高压交流输变电工程架空输电线路施工货运索道施工管理规定(试行)[S]. 北京:国家电网公司交流建设分公司,2013.
[13]中国电力科学研究院. 输电线路工程货运架空索道运输标准化手册:设计篇[S].北京:中国电力科学研究院,2009.
[14]中国电力科学研究院. 输电线路工程货运架空索道运输标准化手册:施工运行篇[S].北京:中国电力科学研究院,2009.

