常用坐标系间GNSS基线向量误差转换方法研究*
孙小荣 李明峰 刘支亮 卞和方
1)宿迁学院建筑工程系,宿迁 223800
2)中国矿业大学国土环境与灾害监测国家测绘地理信息局重点实验室,徐州 221116
3)南京工业大学测绘学院,南京210009
GNSS 相对定位得到的是两点在空间直角坐标系下的基线向量(ΔX,ΔY,ΔZ)及其协方差阵,而在GNSS 控制网二维平差中,需已知两点在高斯平面直角坐标系下的基线向量(Δx,Δy)及其协方差阵DΔxy[2-5],因而须将GNSS 基线向量误差从空间直角坐标系转换到大地坐标系、再从大地坐标系转换到高斯平面直角坐标系[3-5]。文献[4-5]推导了上述误差转换公式,但均假设基线向量的起点位于零子午线上,而实际起点可能位于全球的任何位置。在大地坐标系下,基线向量以角度量表示的误差在数值上非常小,且同一经差所对应的平行圈弧长在不同纬度处会相差较大,不利于实际应用[6-7]。本文借助子午圈曲率半径和平行圈半径将角度量误差转换为以长度为单位的误差(等效长度量误差)。在此基础上,研究GNSS 基线向量误差从空间直角坐标系到站心直角坐标系的转换。理论和算例证明,本文推导的严密公式是正确的,而后两种简化公式可代替此严密公式,且形式更为简单。
1 ΔXij、ΔYij、ΔZij 误差转换为ΔBij、ΔLij、ΔHij误差
设空间直角坐标系下基线向量的起点为i(Xi,Yi,Zi),终点为j(Xj,Yj,Zj),则基线向量ij 的(ΔXij,ΔYij,ΔZij)与其大地坐标差(ΔBij,ΔLij,ΔHij)的关系式为:

式中,Ni、Nj分别为i、j 点法线与椭球面交点的卯酉圈曲率半径。
为将式(1)展开成关于ΔBij、ΔLij、ΔHij的级数形式,需使用以下级数公式:

式中,Bj= Bi+ ΔBij,Lj= Li+ ΔLij,同理Hj= Hi+ΔHij。式(1)关于ΔBij、ΔLij、ΔHij的级数式展开到三阶项即可满足精度要求[4]。
将Nj展开到二阶项为:

为公式推导及计算方便,令

再令ne0=n0(1-e2),ne1=n1(1-e2),ne2=n2(1-e2),nh0=n0+h0,neh0=ne0+h0。将式(2)、(3)代入式(1),不考虑关于ΔBij、ΔLij、ΔHij的四阶及以上项,略去复杂的推导过程,经整理得ΔXij、ΔYij、ΔZij关于ΔBij、ΔLij、ΔHij的级数式为:

式中,
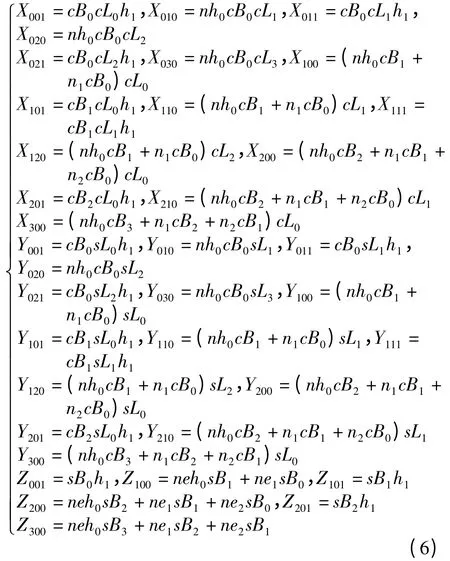
将式(5)对ΔBij、ΔLij、ΔHij求偏导数,得:

式(5)的全微分形式为:
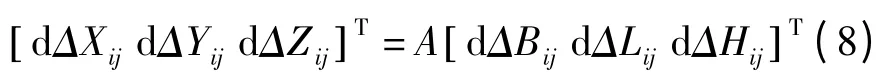
式中,dΔXij、dΔYij、dΔZij、dΔHij以m 为单位,dΔBij、dΔLij、ρ=180/π×3 600,以″为单位。

因A是可逆阵[4],得:

由式(9)及协方差传播定律,得基线向量ij 在大地坐标系下的方差协方差阵为:

2 ΔBij、ΔLij误差转换为Δxij、Δyij误差
由高斯投影坐标正算公式(保留经差的二阶项即可满足精度要求[4])得基线向量ij 的(ΔBij,ΔLij)与(Δxij,Δyij)的关系式为:

式中,Ci、Cj分别为i、j 点到赤道的子午圈弧长。
设高斯投影分带中央子午线经度为L0,i、j 点与中央子午线的经差分别为li=Li-L0,lj=Lj-L0,单位均为rad(图1)。则lj= li+ ΔLij,即得将Ci展开到二阶项为:

图1 经差关系Fig.1 Relation of longitude difference

为公式推导及计算方便,令

将式(12)、(13)代入式(11),不考虑关于ΔBij、ΔLij的三阶及以上项,略去复杂的推导过程,经整理得Δxij、Δyij关于ΔBij、ΔLij的级数式为:

式中,

将式(14)对ΔBij、ΔLij求偏导数,得:
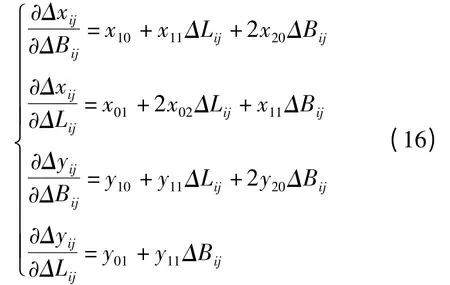
式(14)的全微分形式为:
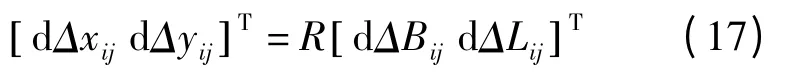
式中,dΔxij、dΔyij以m 为单位,

由式(17)及协方差传播定律,得基线向量ij 在高斯平面直角坐标系下的方差协方差阵为:

3 ΔXij、ΔYij、ΔZij误差转换为Δxij、Δyij误差
转换过程分两步进行。首先将ΔXij、ΔYij、ΔZij误差转换为ΔBij、ΔLij、ΔHij误差,然后将ΔBij、ΔLij误差转换为Δxij、Δyij误差。综合式(9)、(17)得:

式中,S=RC,C 为A-1的第一、二行元素构成的矩阵。
由式(20)及协方差传播定律,得基线向量ij 在高斯平面直角坐标系下的方差协方差阵为:
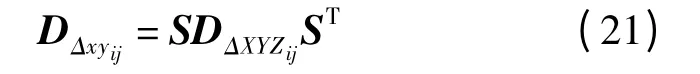
上式即为GNSS 基线向量误差从空间直角坐标系到高斯平面直角坐标系的严密转换公式。
4 ΔXij、ΔYij、ΔZij误差转换为ΔEij、ΔUij误差
由文献[8]可知,在子午圈方向(南北方向)长度达440 km 范围内,可认为地面两点的子午圈曲率半径近似相等,可得M'i=Mi+Hi≈M'j;在平行圈方向(东西方向)任何长度范围内,可认为地面两点的平行圈半径近似相等,可得ri=(Ni+Hi)cosBi≈rj。令,则dΔEij分别表示基线向量ij 的角度量误差引起的沿子午圈方向和平行圈方向的长度量误差,这相当于以子午圈和平行圈上两个微小的曲线长度来表示基线向量ij 在该方向上的误差,则:

垂直方向(法线方向)误差用dΔUij表示,则:

将式(22)、(23)、(24)代入式(9),整理得:
式中,F=AG,G=diag(ρ/M'iρ/ri1),diag(·)表示对角矩阵。
由式(25)及协方差传播定律,得基线向量ij 在大地坐标系下的方差协方差阵为:

5 ΔXij、ΔYij、ΔZij误差转换为误差
由文献[1-3]可知,以基线向量ij 的起点i 为原点,建立站心直角坐标系,则其与空间直角坐标系的关系为:

式(27)的全微分形式为:

由式(28)及协方差传播定律,得基线向量ij 在站心直角坐标系下的方差协方差阵为:

由于Helmert 点位误差度量在2 维和3 维情形下具有旋转不变性,与坐标系的选择无关,即点位方差等于任意两个和三个垂直方向的方差之和[7,9-12],若方向相同,各方向的方差也相等。因ΔN1ij、ΔEij方向分别和Δxij、Δyij及方向相同,若忽略基线向量ij 的高斯投影长度变形、i、j 点大地高(因大地高最大也不会超过9 km,与地球曲率半径相比为微小值)和i 点曲率半径误差的影响,得
6 实例分析
设基线向量(ΔXij,ΔYij,ΔZij)在WGS-84 坐标系中的方差协方差阵为:

取最不利情况:Bi=45°,Li=117°30',Hi=10 000 m,L0=117°,ΔBij=1°,ΔLij=1°,ΔHij=10 000 m。
6.1 ΔXij、ΔYij、ΔZij误差转换为Δxij、Δyij 误差
由式(21)计算得:

6.2 ΔXij、ΔYij、ΔZij误差转换为ΔUij误差
由式(26)计算得:

6.3 ΔXij、ΔYij、ΔZij 误差转换为误差
由式(29)计算得:

表1 4 种坐标系下的误差(单位:m)Tab.1 Errors in the four coordinate systems(unit:m)
由表1 可知,向量误差在空间直角坐标系和站心直角坐标系下其数值是相等的,但与大地坐标系有微小差异,这是由基线起点的曲率半径误差引起的。N1、E 方向误差分别与x、y 及x*、y*方向误差几乎相等,前者的微小差异是由基线向量的高斯投影长度变形及两端点大地高引起的,后者的微小差异是由基线起点的曲率半径误差引起的。U 方向误差与z*方向误差也几乎相等。N1、E、U 方向误差更能直观地反映基线向量误差在3 个重要方向上的大小。
为了与文献[4-5]推导的公式进行比较,将本文前面数据改为Li=L0=0°,其他数据不变,计算该基线向量在大地坐标系、高斯平面直角坐标系下的方向误差和向量误差,结果见表2。
由表2 的结果也能得到类似于表1 的结论。由表1、2 可知,两表中大地坐标系下的向量误差其数值几乎相等,其微小差异是由基线起点的经度不同引起的,两表中方向误差分别相差4.3、3.7 mm,这是公式推导的前提假设不同导致的,基线越长,其差异将越大。
7 结 论
本文高精度地推导了GNSS 基线向量误差从空间直角坐标系到高斯平面直角坐标系的严密和通用转换公式,通过算例验证了公式的正确性。
鉴于严密转换过程分两步进行,且转换矩阵复杂,从本文推导的空间直角坐标系到大地坐标系的全微分公式入手,将大地坐标系中的误差单位统一用长度表示,推导了基线向量误差从空间直角坐标系到大地坐标系的转换公式。理论和算例证明,大地坐标系下3 个参数的误差能直接反映平面和高程上的测量精度,该公式可代替严密公式的转换结果,且误差转换矩阵形式简单,能满足转换精度的要求。
本文也从理论和算例证明,GNSS 基线向量误差从空间直角坐标系到站心直角坐标系的转换公式也可代替严密转换公式,其误差转换矩阵不仅形式更简单,且为正交矩阵,能满足转换精度要求。
1 李征航,黄劲松.GPS 测量与数据处理[M].武汉:武汉大学出版社,2010.(Li Zhenghang,Huang Jinsong.GPS surveying and data processing[M].Wuhan:Wuhan University Press,2005)
2 徐绍铨.GPS 测量原理及应用[M].武汉:武汉大学出版社,2008.(Xu Shaoquan.Principle and application of GPS surveying[M].Wuhan:Wuhan University Press,2008)
3 孔祥元,郭际明,刘宗泉.大地测量学基础[M].武汉:武汉大学出版社,2010.(Kong Xiangyuan,Guo Jiming,Liu Zongquan.Foundation of geodesy[M].Wuhan:Wuhan University Press,2010)
4 刘经南.三维基线向量与大地坐标差间的微分公式及其应用[J].武汉测绘科技大学学报,1991,16(3):70-78.(Liu Jingnan.The formula between 3-D baseline vector and geodetic coordinate differences and its application[J].Journal of Wuhan Technical University of Surveying and Mapping,1991,16(3):70-78)
5 赵长胜,乔仰文.空间三维基线向量大地坐标差与高斯平面二维基线向量间的精度转换[J].测绘工程,1995,4(1):14-19.(Zhao Changsheng,Qiao Yangwen.Precision transformation between space three-dimensional baseline vector geodetic coordinate difference and gaussian plane two-dimensional baseline vector[J].Engineering of Surveying and Mapping,1995,4(1):14-19)
6 施一民.采用新型大地坐标系进行地形变分析的探索[J].大地测量与地球动力学,2007(1):65-68.(Shi Yimin.Analysis of crustal deformation with a new type geodetic coordinate system[J].Journal of Geodesy and Geodynamics,2007(1):65-68)
7 卞和方.在常用坐标系下GNSS 点位误差转换方法研究[J].大地测量与地球动力学,2012(4):83-86.(Bian Hefang.On GNSS positional error transformation between common coordinate systems[J].Journal of Geodesy and Geodynamics,2012(4):83-86)
8 施一民,朱紫阳,范业明.坐标参数为长度量的一种新型的大地坐标系[J].同济大学学报:自然科学版,2005,33(11):1 537-1 540.(Shi Yimin,Zhu Ziyang,Fan Yeming.New form of geodetic coordinate system taking two length quantity as coordinate parameters[J].Journal of Tongji University:Natural Science,2005,33(11):1 537-1 540)
9 张书毕.测量平差[M].徐州:中国矿业大学出版社,2008.(Zhang Shubi.Surveying adjustment[M].Xuzhou:China University of Mining and Technology Press,2008)
10 蔡剑红.一种新的点位误差度量[J].测绘学报,2009,38(3):276-279.(Cai Jianhong.A new measure of positional error[J].Acta Geodaetica et Cartographica Sinica,2009,38(3):276-279)
11 杨元喜.关于“新的点位误差度量”的讨论[J].测绘学报,2009,38(3):280-282.(Yang Yuanxi.Discussion on“A new measure of positional error”[J].Acta Geodaetica et Cartographica Sinica,2009,38(3):280-282)
12 卞和方.点位误差位置相关性分析及验证[J].中国矿业大学学报,2013,42(1):129-133.(Bian Hefang.Analysis and validation of location correlation for positional error[J].Journal of China University of Mining & Technology,2013,42(1):129-133)

