带有记忆的热弹盘方程整体吸引子的存在性

马志勇

带有记忆的热弹盘方程整体吸引子的存在性

马志勇

(上海第二工业大学理学院,上海201209)

研究了带有记忆的热弹盘模型整体吸引子的存在性。在已知解的衰减结论下,建立恰当的符号空间,利用能量方法通过抬高初值正则性,得到解的渐近正则性结果,同时在Kuratowski测度下,证明了吸收球的紧性,最终得到吸引子的存在性。

热弹盘;吸引子;整体存在

0 引言

热弹性是通过温度变化引起固体弹性模量变化的性质[1-2],粗略地说,它既具有某些弹性固体材料的性质,又具有某些黏性流体的性质。热弹方程是热弹性力学方程组的简称,是根据热弹性体的变形和温度的分布规律建立的数学模型。关于材料的弹性、黏性性质的研究历史悠久,近几十年来,新型复合材料、功能材料、生物材料、建筑材料等材料科学的发展,愈来愈深入地涉及到热黏弹性性质。对于本文研究的热弹模型,Romero和Kranosel’skii等[4]也进行了研究,前者在La Salle原则下证明了解不是指数衰减的,但并没有给出任何衰减率,后者在提高初值正则性后证明了解是呈多项式衰减的。本文证明此方程吸引子的整体存在性。

1 模型介绍及分析

本文研究下面的黏弹方程:

初值为:

边值为:

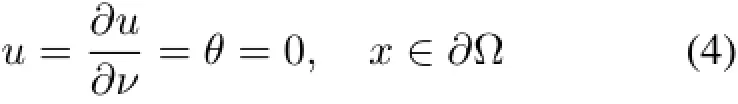
式中:u,θ分别代表位移和温度;x,t分别表示空间和时间变量;Ω是Rn中的一个集合;u0,u1,θ0以及ψ是给定的函数;ρ,c,m,γ为常数;函数k是记忆核函数。定义µ(s)=-k＇(s),给函数µ一些假设条件:

其中,σ为大于0的常数。

同时装备有内积:

进一步有

令Φ=(u,v,θ,ηt),Φ0=(u0,v0,θ0,η0),这样原方程组可变为下面的形式:

式中,A是定义在空间M上的线性算子,

算子A的定义域为

2 已有的结论

下面这些已有的结论[3-4]说明了该模型解的整体存在性,以及大时间性态。

引理1.1算子A是C0半群S(t)的极小生成元。

引理1.2如果Φ0∈D(A),那么一定存在常数

C使得:

进一步对任意的m∈N成立:

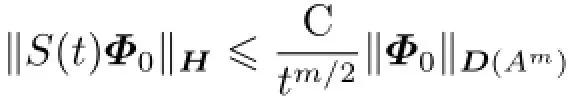
3 结论

定理1.1在假设条件式(5)成立下,式(1)～(4)存在唯一整体吸引子Λ。

下面将利用上面已有的结论证明该模型吸引子的存在性。采取的方法是通过提高初值正则性得到解的渐近正则性,同时证明吸收球的存在性以及紧性,进而通过定义证明吸引子的存在性。

证明为了便于证明,作变量代换,令ut=v,这样式(1)、(2)转变为下面的形式:

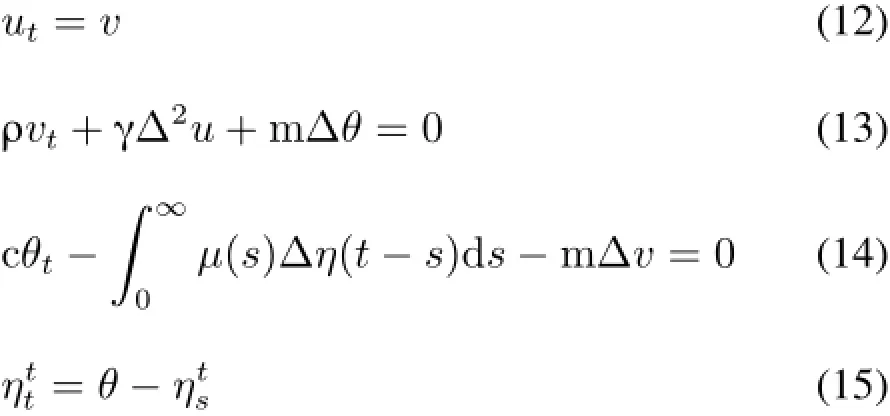
在下面的Hilbert空间中考虑式(12)～(15):

当紧集Λ⊂H满足下面两个条件时就变为吸引子:

(1)Λ是关于S(t)的不变集,即对任意的t满足S(t)Λ=Λ;

由引理1.2的结果可得到对于C0半群S(t)存在有界吸收集ℜ∗⊂H,即对于任意的有界集ℜ⊂H成立:

接下来,定义线性算子A满足Af=-f,众所周知,A是L2上的正定算子,定义域为D(A)= H2∩H10,进一步定义算子As,在其定义域为V2s= D(As)上装备内积:

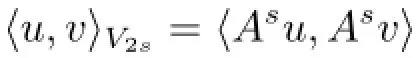
特别地,V-1=H-1,V0=L2,V1=H10,当s1＞s2时,Vs2|←Vs2是紧嵌入,定义Hilbert空间:

很明显,H0=H。

现在,令Φ0=(u0,v0,θ0,η0)∈ℜ0,其中ℜ0为半群S(t)的不变吸收集,在H0中对式(12)～(15)两边分别与〈Aσu,Aσv,Aσθ,Aσηt〉做内积得到:

定义下列函数:

这里qk∈C2,在边界Γ满足qk=νk,这样我们定义下面的函数:

类似于引理1.1、引理1.2和文献[3]中定理1.1的证明,选择合适的系数,得到:

利用紧嵌入[8]:

同时定义空间G(t)=ℜ(t)×B(t)⊂H,由式(19)可得,G(t)是H中的紧集,同时,对任意固定的t≥0以及当时,一定成立:

这里αH表示Kuratowski测度。

由于ℜ0是不变、联通、紧的吸收集且满足式(20),故利用吸引子经典理论[9],可以断定ω-极限集,即

是整体吸引子。这样就完成了定理1.1的证明。

4 结语

本文通过能量方法证明了带有记忆的热弹盘模型整体吸引子的存在性,此方法还可应用到其他带有能量耗散性质的偏微分方程中去。

[1]马志勇,罗琳.带有记忆的黏弹方程解的整体存在性[J].上海第二工业大学学报,2011,28(2):103-105.

[2]马志勇,秦玉明.热弹方程组及相关模型整体适定性的研究[D].上海:东华大学,2009.

[3]ROMERO P G.Polynomial dacay to thermoelastic plateswith memory[J].Quarterly of Applied Mathematics,2009, 3:553-558.

[4]KRASNOSEL’SKII M A,VAINIKKO G M,ZABREIKO P P,et al.Approximate solution of operator equations[M]. Groningen:Noordhoff,1972.

[5]TEMAM R.Infnite-dimensional dynamical systems in mechanics and physics[M].New York:Springer-Verlag, 1988.

[6]PATA V,ZUCCHI A.Attractors for a damped hyperbolic equation with linear memory[J].Adv Math Sci Appl, 2001,11:505-529.

[7]HALE J.Asymptotic behavior and dynamics in infnite dimensions[M].Boston:Pitman,1985.

[8]QIN Y.Nonlinear parabolic-hyperbolic systems and their attractors[M].Basel:Boston-BerlinBirkhauser,2008.

[9]PAZE A.Semigroups of linear operators and applications to partial differential equations[M].Berlin:Springer-Verlag,1983.

Global Attractors for Thermoelastic Plates with Memory

MA Zhi-yong
(School of Science,Shanghai Second Polytechnic University,Shanghai 201209,P.R.China)

The thermoelastic plates with memory is considered.The existence of the global attractor for this system is given.Under the decay result of the solution and the symbol space properly,by using the energy method through raising the initial regularity,the asymptotic regularity results of solutions is proven.At the same time in the Kuratowski measure,the global attractor follows directly from the compactness of the absorption ball is proved.

thermoelastic plates;attractors;global exist

O29

A

1001-4543(2014)04-0316-04

2014-06-26

马志勇(1980–),男,河南安阳人,副教授,博士,主要研究方向为偏微分方程。电子邮箱zyma@sspu.edu.cn。

数学天元基金(No.11326047)、上海市优青资助计划项目(No.zzegd12006)、上海第二工业大学曙光研究院应用数学研究所项目No.A30XK121y03)、上海第二工业大学重点学科项目(No.XXKZD1304)资助