关于二元函数极值判别法的改进
冯守平
(安徽财经大学统计与应用数学学院,安徽蚌埠233030)
关于二元函数极值判别法的改进
冯守平
(安徽财经大学统计与应用数学学院,安徽蚌埠233030)
提出了将二元函数极值化为一元函数极值的一种新方法;给出了二元函数极值存在的充分必要条件,改进了二元函数极值的判别法;并给出了判别式Δ=fxx(P0)fyy(P0)-fxx2(P0)的几何意义.
数学分析;极值判别法;充分必要条件;判别式的几何意义
设二元函数z=f(P)在区域D上连续,P0(x0,y0)为D0的驻点或偏导数不存在点.过点(x0,y0,0)作平行于z轴的平面簇:

此平面簇与二元函数z=f(P)所代表的空间曲面相交所得到的交线簇为:

在本文的讨论中均假设涉及到的邻域U(P0,δ)⊂D0.
定理1设P0为f(P)在的驻点D0或偏导数不存在点,则:f(P0)是f(P)的极小(大)值⇔∃δ>0,∀k∈R,当P (x,y0+k(x-x0))∈U(P0,δ)时,恒有:

证"⇒"设f(P0)是f(P)的极小值,由定义,∃δ>0,∀P∈U(P0,δ),有f(P)≥f(P0).因此∃δ>0,∀k∈R,当P (x,y0+k(x-x0))∈U(P0,δ)时,有f(P)≥f(P0).这说明在U(P0,δ)的每条直线y=y0+k(x-x0)(k∈R)上,一元函数f(x,y0+k (x-x0))恒取得极小值f(P0).
"⇐"设∃δ>0,对∀k∈R,当P(x,y0+k(x-x0))∈U(P0,δ)时,恒有f(P)≥f(P0),即在U(P0,δ)内的每条直线y=y0+k(x-x0)上,一元函数f(P)都取得极小值f(P0);按极小值定义,还需要证明在U(P0,δ)内的直线x=x0上,当 (x0,y)∈U(P0,δ)时,有f(x0,y)≥f(P0).若在直线x=x0上∃已知f(P)在D上连续,,恒有f(P)=f(x,y0+k(x-y0)) 由定理1的充分条件知:若在驻点P0的邻域U(P0,δ)内的所有直线y=y0+k(x-y0)上,一元函数z=f(x,y0+k (x-y0))恒在x0取得极小(大)值,则二元函数f(P)就在P0取得极小(大)值.在判别极值过程中并不需要再研究直线x=x0上情形,这简化了判别过程. 在定理1的充分条件中要求存在点P0的某个邻域U(P0,δ),这里要求针对∀k∈R,存在统一的δ,这一要求是必不可少的,如例1. 例1讨论f(x,y)=(y-x2)(y-2x2)在点(0,0)是否存在极值[1]. 解易知点(0,0)是f(x,y)的驻点,但(0,0)不是f(x,y)的极值点.这里对一元函数:来 说,∀k∈R,均∃δk>0.当(x,0+k(x-0))=(x,kx)∈U((0,0),δk)⊂R2时,函数: 即∀k∈R,f(x,kx)均在x=0取得极小值0,但不存在定理1中统一的δ>0,因为对∀δ>0,当(x,kx)∈U((0,0),δ)⊂R2时,可选择适当x,k使(2)式中的k-x与k-2x异号,从而f(x,kx)的值有正有负,故f(0,0)=0不是极值. 注若对某个k,一元函数f(x,y0+k(x-x0))在x=x0无极值,则二元函数f(x,y)在(x0,y0)无极值;若对两个不同的k,f(x,y0+k(x-x0))在x=x0虽有极值,但不同,则二元函数f(x,y)在(x0,y0)也无极值. 例2讨论f(x,y)=exy2+x2y3+2在驻点(0,0)是否有极值[2]. 解易验证判别式.在直线y=x上: 显然x=0是f(x,y)的驻点,而: 定理2设二元函数f(P)在区域D上连续,P0为D0驻点或偏导数不存在点.∀k∈R,当P=(x,y0+k(x-x0))∈D时,恒有: 则P0是f(P)在D上的最小(大)值点. 定理2的证明与定理1的充分条件证明类似. 定理2说明:若对∀k∈R,(x,y0+k(x-x0))∈D,f(x,y0+k(x-x0))恒在点x0取得最小(大)值,则二元函数f(P)就在驻点或偏导数不存在点P0取得最小(大)值. 定理3P0是f(P)在区域D0的驻点⇔∀k∈R,x=x0为一元函数f(x,y0+k(x-x0))的驻点. 定理4设f(P)在驻点P0的某邻域U(P0,δ)有连续二阶偏导数,且A2+B2+C2≠0,则∀P∈U(P0,δ),△(P)≥0⇔P0是f(P)的极值点. 当P0是f(P)的极值点时,若A>0(<0)或C>0(C<0),则P0是f(P)的极小(大)值点. 证"⇒"设∃δ>0,∀P∈U(P0,δ),△(P)≥0.当△(P0)>0时,若A=fxx(P0)>0(<0),∃P0的某邻域,不妨设定理4中的邻域U(P0,δ),在此邻域中,fxx(P)>0(<0),△(P)≥0,则∀k∈R,P=(x,y0+k(x-x0))∈U(P0,δ),有: 所以,∀k∈R,驻点x=x0恒是一元函数f(x,y0+k(x-x0))的极小(大)值点,由定理1知P0是f(P)的极小(大)值点. 当△(P0)=AC-B2=0,A>0(<0)时,∃U(P0,δ),∀P∈U(P0,δ),fxx(P)>0(<0),△(P)≥0,∀k∈R;当P=(x,y0+k(xx0))∈U(P0,δ)时,有: 所以,∀k∈R,驻点x=x0恒是一元函数f(x,y0+k(x-x0))的极小(大)值点,由定理1知P0是f(P)的极小(大)值点. 当A=0时,若C=0,则由△(P0)=AC-B2=0,知B=0,这与定理4中条件A2+B2+C2≠0矛盾,所以C2≠0.仿上文对A>0(<0)情形的讨论可知,当C>0(C<0)时,P0也是f(P)的极小(大)值点. "⇐"设P0是f(P)的极值点.若∀δ∈0,∀P∈U(P0,δ),△(P)≤0(≢0),当C=fyy(P0)≠0时,不妨设C>0,于是∃U(P0,δ),∀P∈U(P0,δ),fyy(P0)>0,且△(P)≤0(≢0).此时: 都与k有关,都在闭圆U¯(P0,δ1)(⊂U(P0,δ))上连续,设它们分别在U¯(P0, δ1)上的点(x1,y0+k1(x1-x0))与(x2,y0+k2(x2-x0)),(x3,y0+k3(x3-x0))与(x4,y0+k4(x4-x0))处取得最小值、最大值m-与M-,m+M+,即: 由于∀δ>0,∀P∈U(P0,δ1),Δ(P)≢0,显然,m-≤M- 而当k 由定理1知P0不是f(P)的极值点,这与假设矛盾. 当A=fxx(P0)≠0时,类似讨论,并有同样的结论. 若A=C=0由定理4条件A2+B2+C2≠0知B=fxy(P0)≠0.此时,二阶导数: 在点P0充分小邻域内的符号由2fxy(P)k中的k的符号来确定,由定理1知P0不是f(P)的极值点,这与假设矛盾. 若∀δ>0,∀P>U(P0,δ),Δ(P)有正有负,0<θ<1,由二元函数泰勒公式,得: 若A=fxx(P0)>0(<0),∃U(P0,δ),∀P∈U(P0,δ),fxx(P)>0(<0).设P1∈U(P0,δ),Δ(P1)<0,则∃U(P1,δ1)⊂U(P0,δ1),∀P∈U(P1,δ1),Δ(P)<0.此时∃k1,k2,k1 设P2∈U(P0,δ),Δf(P2)>0,则∃U(P2,δ2)⊂U(P0,δ),∀P∈U(P2,δ2),Δ(P)>0.此时与上面情形类似,∃k3,k4, k3 根据上述讨论,由定理1知P0不是f(P)的极值点,这与假设矛盾. 若C=fyy(P0)>0(<0),类似讨论,并有同样的结论. 若A=C=0,由定理4条件A2+B2+C2≠0知B≠0,此时由(5)知:F(h,k)=fxx(x0+θh,y0+θkh)+2fxy(x0+θh,y0+θkh) k+fyy(x0+θh,y0+θkh)k2,在点P0充分小邻域内的符号由2fxy(x0+θh,y0+θkh)k中的的符号来定,此时,P0不是f(P)的极值点,这与假设矛盾. 注1当A=B=C=0时,若∃δ>0,∀P∈U(P0,δ),Δ(P)≥0,且fxx(P)≥0(≤0),则P0是f(P)的极小(大)值点.由公式(3)易知结论成立.由此结合定理4可知:不论A,B,C取何值,只要条件"∃δ>0.∀P∈U(P0,δ),Δ(P)≥0"满足,P0就是f(P)的值点. 注2若∃δ>0,∀P∈U(P0,δ),Δ(P)≤0(≢0),则P0是否为f(P)的极小(大)值点,需另行判别. 如xy2,x2y2都属于情形注2:对前者,∀P∈U((0,0),Δ(P)=-4y2≤0),易知它在点(0,0)无极值;对后者,∀P∈U((0,0),Δ(P)=-12x2y2≤0,易知它在点(0,0)有极小值. 注3公式(3)给出了判别式Δ(P0)=AC-B2的几何意义:设f(P)在驻点P0某个邻域内有连续的二阶偏导数,若Δ(P0)>0,A>0(<0),则∃δ>0,∀P∈U(P0,δ)使空间中过点的曲线:在点(x0,y0,z0)附近是下(上)凸的. 例3求函数f(x,y)=x2+y4+3的极值[2]. 解f的驻点为(0,0),易知它是极小值点,用定理4判别. fxx=2,fxy=0,fyy=12y2,Δ(0,0)=AC-B2=0,A2+B2+C2=4≠0.∀(x,y)∈U(0,0),Δ(x,y)=2X12y2-0=24y2≥0,又A=2>0,由定理4知,f(0,0)是f的极小值. 例4(最小二乘法)证明:在最小二乘准则 证易知有惟一的驻点(a0,b0),由定理3知,∀k∈R,a=a0是f(a,b0+k(a-a0))的惟一驻点.∀k∈R,f(a,y0+k(a-x0))∈U(x0,y0),有所以,∀k∈R,a=a0是一元函数f(a,b0+k(a-b0))的极小值点,同时也是最小值点,由定理2知(a0,b0)是f(a,b)在R2中的最小值点. 由定理2及定理4得: 推论设f(P)在区域D上有连续二阶偏导数,在D0有惟一驻点P0,且∀k∈R,一元函数f(x,y0+k(x-x0))仅有一个驻点x0,则当Δ(P0)=AC-B2>0,A>0(<0)时,x0恒是f(x,y0+k(x-x0))的最小(大)值点,从而P0是二元函数f(P)在D上的最小(大)值点. 例5证明:若二元二次有理整式函数f(x,y)=ax2+bxy+cy2+dx+ey+g(a2+b2+c2≠0)有惟一的极值点,则该点就是最值点. 证令 当(6)式的系数行列式4ac-b2≠0时,解(6)式可得f(x,y)在R2内惟一驻点(x0,y0).又: 所以,∀k∈R,x=x0是f(x,y0+k(x-x0))的惟一驻点.若Δ(x0,y0)=AC-B2=4ac-b2>0,a>0(<0),则: 即∀k∈R,f(x,y0+k(x-x0))在惟一驻点x=x0处取得极小值(极大值),它也是最小(大)值,由定理4的推论知,f (x0,y0)也是f(x,y)在R2内的最小(大)值. 对二元函数f(x,y)来说,当f(x,y)仅有一个驻点(x0,y0),该点又是极值点,由文[3]和文[4]知该点未必就是最值点,但对二元二次有理整式函数来说,若它有惟一极值点,则该极值点就是最值点.二元二次有理整式函数是空间解析几何及经济数学的主要研究对象之一,在文献[1]、[2]、[5]等中也是常见的. 以上是针对二元函数讨论的,对一般的多元函数,笔者认为也应有类似定理4的结论. [1]华东师范大学数学系编.数学分析:下册[M].3版.北京:高等教育出版社,2001:138-139. [2]Raymond A,Barnett,M R,Ziegler K E,etal.Calculus[M].9版.高等教育出版社,2005:509-516. [3]冯守平.求多元函数最值中值得注意的一个问题[J].高等数学研究,2007,10(2):23-24. [4]菲赫金哥尔茨.微积分教程:第一卷:第二分册[M].北京:人民教育出版社,1957:435. [5]Finney W G.托马斯微积分[M].叶齐孝,译.北京:高等教育出版社,2003:964-970. On the im provement of the discrim inantm ethod of binary function extreme value FENG Shou-ping The paper discusses a new method of transforming the binary function extreme value into the linear function extreme value by providing the sufficient and necessary conditions of the existence of the binary function extreme value,and hence improves the discriminantmethod.It also gives the geometric meaning of the discriminant function mathematical analysis;discriminant method of extreme value;the sufficient and necessary conditions;the geometricmeaning O172 :A :1007-5348(2014)06-0011-05 (责任编辑:邵晓军) 2014-02-18 国家自然科学基金青年项目(61305070). 冯守平(1954-),男,安徽淮南人,安徽财经大学统计与应用数学学院教授,主要从事函数论及数量经济数学方面的研究.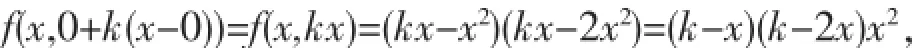










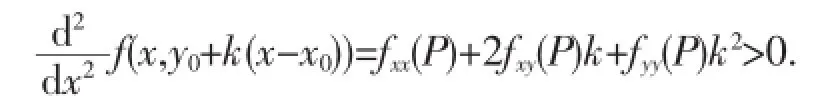




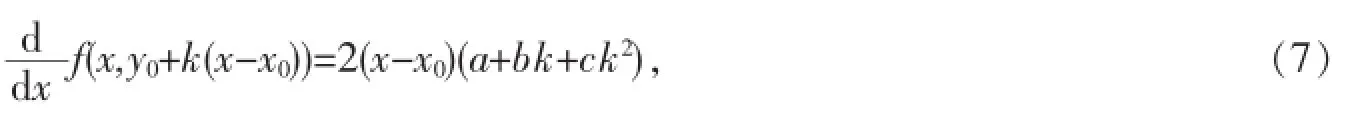

(School of Statistics&Applied Mathematics,Anhui University of Finance and Economics, Bengbu 233030,Anhui,China)

