高斯尺度混合大气噪声模型的参数估计*
应文威,李成军,冯士民
(1.91635部队,北京102249;2.海军工程大学兵器工程系,湖北武汉430033)
高斯尺度混合大气噪声模型的参数估计*
应文威1,李成军1,冯士民2
(1.91635部队,北京102249;2.海军工程大学兵器工程系,湖北武汉430033)
非高斯大气噪声的参数估计对甚低频、超低频信号的最佳接收有重要意义。对大气噪声采用基于逆高斯分布的高斯尺度混合分布模型建模,研究了基于逆高斯分布的高斯尺度混合分布模型参数的性质,设计了高斯尺度混合大气噪声模型参数的马尔可夫链蒙特卡罗(MCMC)算法。算法在贝叶斯层次模型下,采用Gibbs抽样和M-H抽样更新参数。仿真结果表明,该模型对大气噪声有很好的适用性,MCMC算法迭代效率和精度高,具有实际的应用价值。
高斯尺度混合 逆高斯分布 大气噪声 马尔可夫链蒙特卡罗
0 引 言
甚低频和超低频通信系统中,对噪声的建模都是基于高斯分布,然而在实际应用中,受雷电等产生的大气噪声的影响,噪声往往具有明显的非高斯特性[1]。为了实现最佳接收,必须对噪声进行参数估计。对噪声的参数估计,传统上采用最大期望算法或最大似然估计[2-4];对噪声的建模也以对称α稳定分布居多[5-6]。高斯尺度混合分布模型是更广泛意义上的非高斯分布模型,近年来受到广泛关注。基于逆高斯分布的高斯尺度混合分布模型,具有更好的高尖峰、重拖尾特性,能很好反映大气噪声的非高斯特性[7-9]。同时,由于该模型参数较多,概率密度计算难度大,精度也不够理想,所以本文采用马尔可夫链蒙特卡罗(MCMC,Markov chain Monte Carlo)算法,设计了基于逆高斯分布的高斯尺度混合分布模型下的参数估计算法。
MCMC算法,能够解决具有高维度且形式复杂的未知参数的后验概率计算问题,是一种在统计计算中性能优越的方法[10-11]。本文通过设计MCMC层次算法来估计混合模型的参数,迭代收敛快,精度高,具有明显的优势。
1 高斯尺度混合分布模型
1.1 高斯尺度混合分布模型
高斯尺度混合分布模型是由高斯分布的随机变量和非负尺度随机变量混合形成的,其表达式为:

式中,g服从0均值的高斯分布g~N(0,δ2),概率密度函数为:
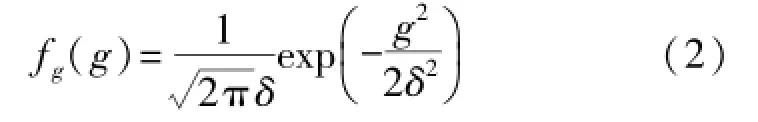
式中,τ为非负尺度的随机变量,典型的分布可以取为伽马分布,逆伽马分布等。为了更好的拟合大气噪声特征,文中τ服从逆高斯分布τ~IG(μ,λ),其中μ为形状参数,λ为尺度参数,其概率密度函数的表达式为:
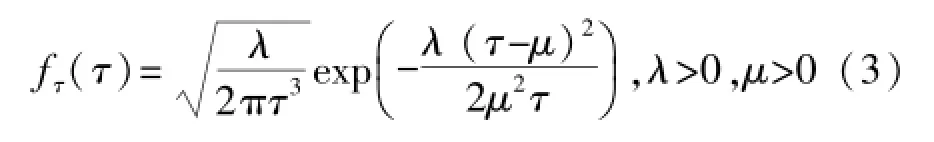
通过对随机变量x的概率密度函数的计算可以发现,随机变量x的概率密度函数的表达式复杂,难以用解析表达式表达。
1.2 性质
通过对上述高斯尺度混合分布概率密度函数的特征函数的计算,不难证明有如下性质:
性质若随机变量x=τ1/2g,其中,g服从0均值的高斯分布:g~N(0,δ2),τ服从逆高斯分布:τ~IG(μ,λ),则随机变量x可以等效为:
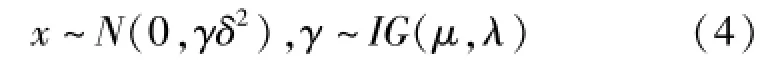
并且,对于上述一个固定的分布,满足μδ2=a,其中a为固定常数。
从上述性质可以得出,对于一个固定的分布,参数δ2,μ,λ不是固定值,可以有多种组合,只有在其中一个参数固定的条件下,才可以确定其他两个参数。
2 贝叶斯层次模型
2.1 大气噪声模型
根据1.2节所述性质,高斯尺度混合分布大气噪声的参数{δ2,λ,μ}满足一定关系,那么可以固定μ=10,则混合模型需要估计的参数为{δ2,λ}。
假设观测到的噪声数据集x={xi,i=0,1,2,…,n},根据式(4),可以得出高斯尺度混合分布大气噪声的等效形式:
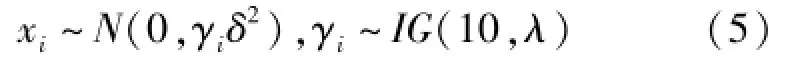
2.2 贝叶斯层次模型
贝叶斯推断通过先验分布来推断后验分布,参数集变量{δ2,λ}的后验分布为:

选取合理的共轭先验能够充分利用先验信息,这使得贝叶斯模型的性能显著提高,对上述参数选取以下先验分布:
参数δ-2的共轭先验分布为伽马分布:δ-2~Γ(α,β),其中α和β分别为伽马分布的形状参数和逆尺度参数。
参数λ的后验概率分布计算复杂,难以得到其共轭先验分布,所以λ取惯常的先验分布,为伽马分布:λ~Γ(ξ,τ)。
为了使超参数β,τ具有更强的灵活性,增加两个额外层,他们的共轭先验分别为:β~Γ(g,h),τ~Γ(κ,ε)。
为了直观表述参数之间的关系,画出高斯尺度混合分布模型各参数的直接非循环图,图中圆圈代表参量,是需要估计的值,方框代表定值,如图1所示。
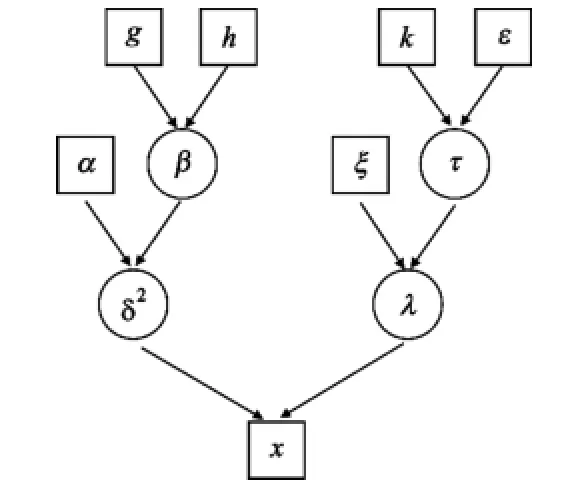
图1 模型的直接非循环Fig.1 Direct acyclic graph specific to the model
3 MCMC算法
在MCMC算法中,常采用Gibbs抽样和Metropolis-Hasting(M-H)抽样算法对更新参数进行抽样。本文对于容易计算的、常见的后验概率采用Gibbs抽样,对复杂、不常见的后验概率采用M-H抽样。具体算法流程如下:
步骤1通过Gibbs抽样更新参数δ2。
步骤2通过M-H算法更新参数λ。
步骤3通过Gibbs抽样更新参数β,τ。
步骤4通过M-H算法更新变量{γi}。
3.1 通过Gibbs抽样更新参数δ2
δ-2的全条件后验分布为:
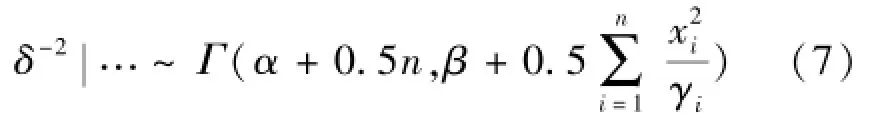
通过Gibbs抽样,生成新的伽马分布随机数对δ2进行更新。
3.2 通过M-H算法更新参数λ
λ的全条件后验概率为:

因为λ的全条件后验概率复杂,不是常见的分布,所以通过M-H抽样算法更新λ值,算法步骤如下:
1)λ选用建议分布为q():μ~N(λ(t),0.1)。
2)从1)中抽样λ′作为备选值。
3)从均匀分布中生成随机数u~U(0,1)。
4)计算接受概率R=min(1,A),其中:

因为建议分布是对称的,所以式(14)可以化简为:
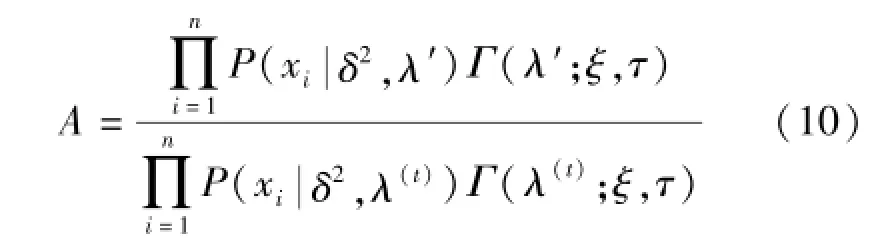
5)若u≤R,则接受新值λ(t+1)=λ′,否则不接受新值,则λ(t+1)=λ(t)。
3.3 通过Gibbs抽样更新参数β,子
β,τ的全条件后验分布分别为:
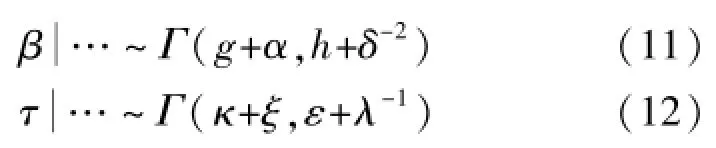
通过Gibbs抽样,生成新的伽马分布随机数对β,τ进行更新。
3.4 通过M-H算法更新变量{γi}
γ的全条件概率分布为:
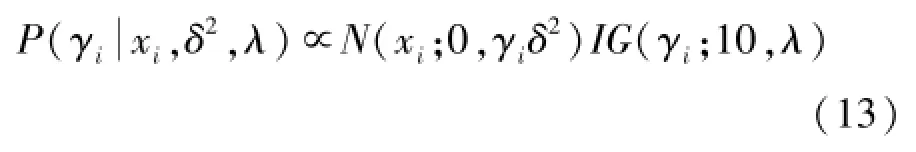
1)γi选用建议分布为:γi~IG(10,λ)。
2)从1)中抽样γi'作为备选值。
3)从均匀分布中生成随机数u~U(0,1)。
4)计算接受概率:
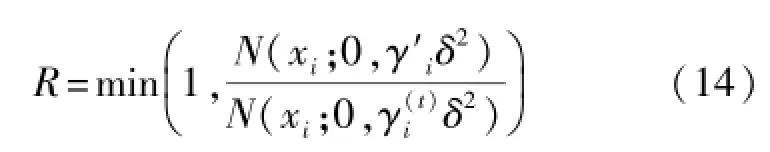
5)若u≤R,则接受新值,否则不接受新值,则。
4 仿真及测试
仿真实验中,将混合模型的参数设置为δ2=1,λ=0.5,仿真数据数目设为n=2 000。超参数简单的设置为α=0.5,β=1,ξ=0.5,τ=1,g=2,h=1,κ= 2,ε=1。设置算法的预烧期为400,总迭代次数为1 000。仿真的结果如图2和图3所示。
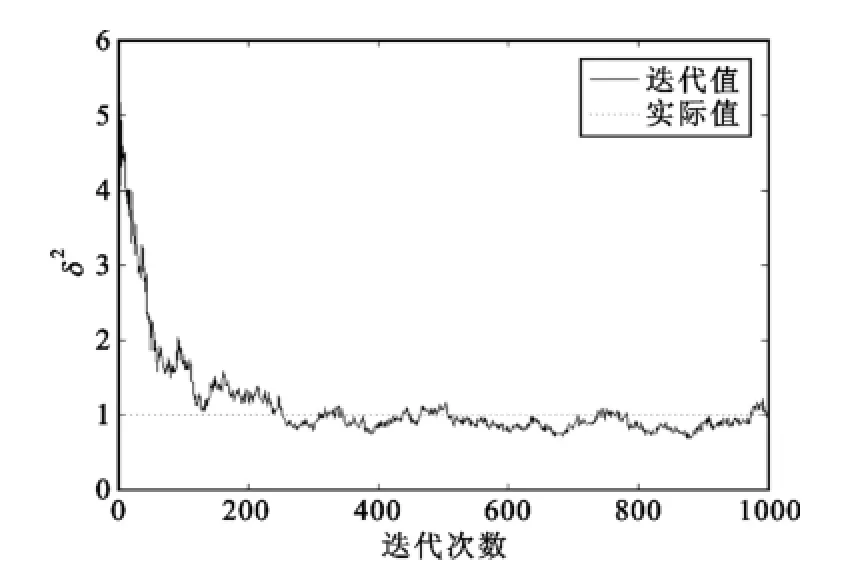
图2 δ2的迭代收敛Fig.2 Time-average convergence ofδ2
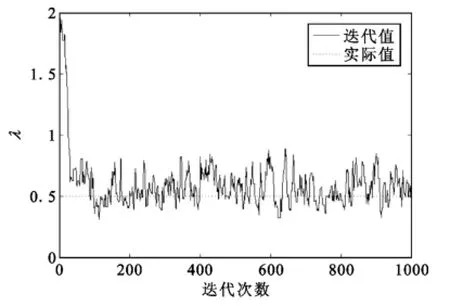
图3 λ的迭代收敛Fig.3 Time-average convergence ofλ
从各参数的迭代收敛情况可以看出,在进行200次迭代后,各参数就收敛到实际值。对预烧期之后的迭代值进行平均,得到各参数的估计结果为δ2=0.971,λ=0.509。
图4为上述参数下噪声模型数据,可以看出其中明显的非高斯特征。图5为用参数的估计结果画出的幅度概率分布(APD,Amplitude Probability Distribution)曲线,圆圈代表仿真的噪声数据的实际值,曲线为用参数的估计值画出的APD曲线(X轴尺度为-0.5 log10(-lnP(>x0)),Y轴尺度为10lg(x0) dB)。从图5中可以看出,估计参数画出的APD曲线与噪声数据吻合的很好,这也说明了本文的模型对大气噪声的适用性,并且,用MCMC算法能对模型参数进行有效估计。
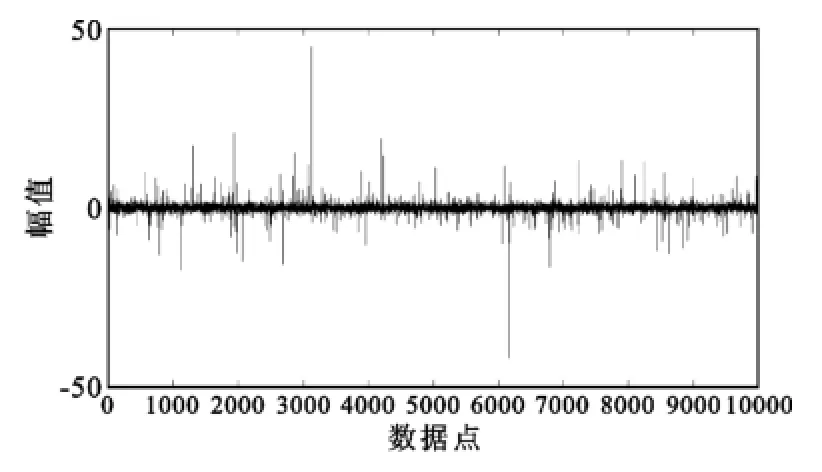
图4 仿真大气噪声数据Fig.4 Simulation data of the atmospheric noise
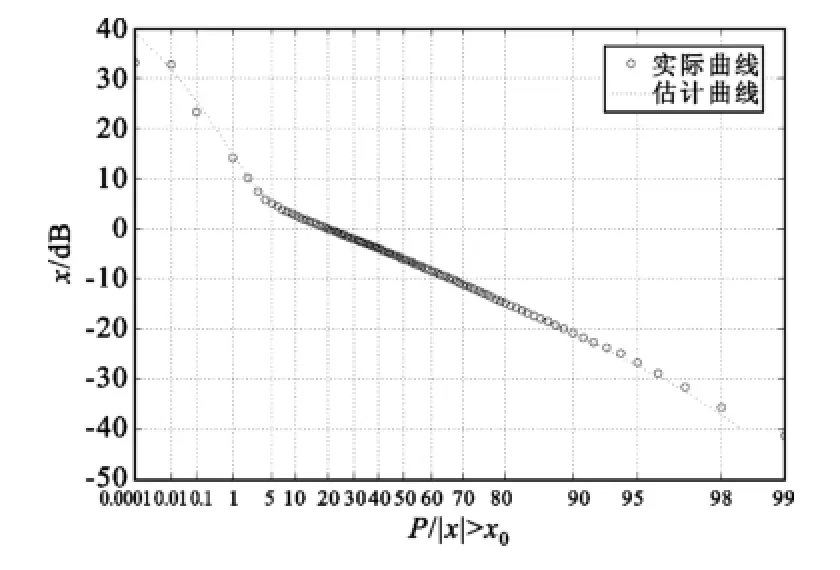
图5 实际仿真数据和估计参数下的APD曲线Fig.5 APD graphs of the actual noise data and noise data with estimation parameters
5 结 语
本文通过对噪声采用基于逆高斯分布的高斯尺度混合分布模型建模,研究了基于逆高斯分布的高斯尺度混合分布模型的性质,将高斯尺度混合分布等价为高斯分布,使算法有更高的迭代效率和精度。通过设计贝叶斯层次模型,采用MCMC算法,对参数通过Gibbs抽样和M-H抽样算法进行更新和估计。仿真结果表明,该模型对大气噪声有很好的适用性,MCMC算法迭代效率和精度高,对水下低频非高斯噪声下通信接收有实际的意义。
[1] 施意,张爽,张昕.大气噪声对甚低频通信系统干扰仿真分析[J].通信技术,2013,46(09):32-34.
SHI Yi,ZHANG Shuang,ZHANG Xin.Simulation and Analysis of Atmospheric Noise Interference on VLF/LF Communication[J].Communications Technology,2013, 46(9):32-34.
[2] 赵宜楠,李风从,尹彬.严重拖尾复合高斯杂波中目标的自适应极化检测[J].电子与信息学报,2013, 35(02):376-380.
ZHAO Yi-nan,LI Feng-cong,YIN Bin.Adaptive Polarimetric Detection of Targets in Heavy-Tailed Compound-Gaussian Clutter[J].Journal of Electronics&Information Technology,2013,35(2):376-380.
[3] WANG J,ALEKSANDAR D,and ARYE N.Maximum Likelihood Estimation of Compound-Gaussian Clutter and Target Parameters[J].IEEE Transactions on Signal Processing,2006,54(10):3884-3898.
[4] BALLERI A,NEHORAI A,and WANG J.Maximum Likelihood Estimation for Compound-Gaussian Clutter with Inverse Gamma Texture[J].IEEE Transactions on Aerospace and Electronic Systems,2007,43(02):775-780.
[5] 应文威,蒋宇中,刘月亮.大气低频噪声混合模型的MCMC参数估计[J].系统工程与电子技术,2012, 34(06):1241-1245.
YING Wen-wei,JIANG Yu-zhong,LIU Yue-liang.Parameter Estimation for Mixture Model of Atmospheric Noise through MCMC Method[J].Systems Engineering and Electronics,2012,34(6):1241-1245.
[6] YING Wen-wei,JIANG Yuzhong,and LIU Yue-liang, et al.A Blind Receiver with Multiple Antennas in Impulsive Noise Modeled as the Sub-Gaussian Distribution via the MCMC Algorithm[J].IEEE Transactions on Vehicular Technology,2013,62(07):3492-3497.
[7] LIU B,CHEN Biao,and JAMES H M.A GLRT for Radar Detection in the Presence of Compound-Gaussian Clutter and Additive White Gaussian Noise[C]//Sensor Array and Multichannel Signal Processing Workshop Proceedings.USA:IEEE,2002:87-91.
[8] ESA O,DAVID E T,and VISA K,et al.Compound-Gaussian Clutter Modeling with An Inverse Gaussian Texture Distribution[J].IEEE Signal Processing Letters, 2012,19(12):876-879.
[9] CHEN Sijia,KONG Lingjiang,and YANG Jianyu.A-daptive Detection in Compound-Gaussian Clutter with Inverse Gaussian Texture[J].Progress in Electromagnetics Research M,2013(28):157-167.
[10] PENG Geng,HUANG Zhitao,and WANG Fenghua,et al.Single Channel Blind Signal Separation with Bayesian-MCMC[C]//Wireless Communications&Signal Processing.China:IEEE,2009:1-4.
[11] ANTHONY L,CHRISTOPHER Y,and MICHAEL B G,et al.On the Utility of Graphics Cards to Perform Massively Parallel Simulation of Advanced Monte Carlo Methods[J]Journal of Computational and Graphical Statistics,2010,19(04):769-789.
YING Wen-wei(1987-),male,Ph.D.,majoring in digital signal processing;
李成军(1976—),男,博士,高级工程师,主要研究方向为数字信号处理;
LI Cheng-jun(1976-),male,Ph.D.,senior engineer, mainly engaged in digital signal processing.
冯士民(1987—),男,博士,主要研究方向为通信信号处理。
FENG Shi-min(1987-),male,Ph.D.,mainly engaged in communication signal processing.
Parameters Estimation for Gaussian Scale Mixture Atmospheric Noise
YING Wen-wei1,LI Cheng-jun1,FENG Shi-min2
(1.Unit 91635 of PLA,Beijing 102249,China; 2.Department of Weaponry Engineering,Naval University of Engineering,Wuhan Hubei 430033,China)
Parameters estimation of the non-Gaussian atmospheric noise has an important significance to the signals optimal detection in very low frequency(VLF)and extremely low frequency(ELF)communication.A model based on Gaussian scale mixture(GSM)distribution with inverse-Gaussian is proposed. The characteristic of parameters of GSM distribution with inverse-Gaussian is studied.Markov chain Monte Carlo(MCMC)method is designed to estimate parameters.This method,based on Bayesian hierarchical model,updates the parameters through Gibbs sampler and M-H algorithm.The experimental results show that the proposed model performs well.The MCMC method is of good iterative efficiency and precision,and can be excellently applied in practice.
Gaussian scale mixture(GSM);inverse-Gaussian distribution;atmospheric noise;Markov chain Monte Carlo(MCMC)
TN911.7
A
1002-0802(2014)09-1010-04
10.3969/j.issn.1002-0802.2014.09.007
应文威(1987—),男,博士,主要研究方向为数字信号处理;
2014-06-10;
2014-07-10 Received date:2014-06-10;Revised date:2014-07-10

