标准卷积码在QPSK相位模糊下的研究*

涂 榫,高 勇

(1.四川大学电子信息学院,四川成都610065;2.解放军78009部队,四川成都610066)

标准卷积码在QPSK相位模糊下的研究*

涂 榫1,2,高 勇1

(1.四川大学电子信息学院,四川成都610065;2.解放军78009部队,四川成都610066)

在数字相位调制系统的相干解调过程中,普遍存在着载波相位模糊问题,以往的解决方法是遍历所有可能的相位模糊情况,通过解模糊处理、后续判断来验证每种可能的正确性,效率较低。针对QPSK解调过程中存在的8种相位模糊情况,利用卷积码编码约束关系,分析研究了标准(2,1,m)卷积码和各种码率的删余卷积码在每种相位模糊下其采样校验元的变化情况,以及相位模糊对译码后信息的影响,给出了基于采样校验元检测的相位模糊识别方法。该方法有效降低了相位模糊情况的可能数量,提高了人工观察判断的工作效率。

卷积码 相位模糊 采样校验元

0 引 言

卷积码由于其设备实现简单,编码性能良好,而被广泛应用于实际的通信系统中[1]。正交相移键控(QPSK,Quadrature Phase Shift Keying)调制方式具有较高的频谱利用率、较强的抗干扰性等特点,是卫星传输系统中最常用的调制方式。若在接收端采用相干解调方式,则在恢复载波的过程中,可能出现相位模糊的问题[2],从而导致解调后的数据比特位翻转,降低系统的可靠性。因此接收端必须克服由于同步和相位跳变发生的相位模糊问题,需要进行解模糊处理。以往的解决方法是对全部可能的相位模糊情况均试一遍,通过后续分析来验证每种可能的正确性,没有利用信道纠错编码的约束关系,没有挖掘更多的有用信息。本文结合信道编码和调制2个方面,在利用卷积码编码约束关系的基础上,给出信道编码层次上抗相位模糊处理方法,通过分析标准(2,1,m)卷积码和各码率删余卷积码在每种相位模糊情况下其采样校验元的变化情况,以及相位模糊对译码后信息的影响,给出了基于采样校验元检测的相位模糊识别方法。

1 标准卷积码和QPSK相位模糊情况

1.1 标准卷积码的删除模式及基本校验矩阵

目前卫星通信中常用的卷积码有码率为1/2的非系统卷积码、以及码率为1/2的源卷积码经删除后生成的(n-1)/n型码率的删余卷积码,本文重点对(2,1,6)卷积码及其删余卷积码进行相位模糊的讨论,(2,1,6)标准卷积码的删除模式和基本校验矩阵如表1所示。

表1 (2,1,6)标准卷积码删除模式和基本校验矩阵关系Table 1 (2,1,6)Standard convolution code delete mode and basic check matrix relations

1.2 QPSK相位模糊情况

对于QPSK相位调制系统,采用相干正交支路解调时,通常使用4次方环、costas环等非线性载波恢复方法,从而带来了相位模糊,其相位模糊值可能为00,900,1800或2700,同时还可能存在支路翻转的情况[3]。若未对调制信号调制数据与载波相位做明确约定,相位模糊发生时接收端总共有8种可能的解调结果[4](如表2所示),而每一种解调结果惟一对应一种相位模糊可能。

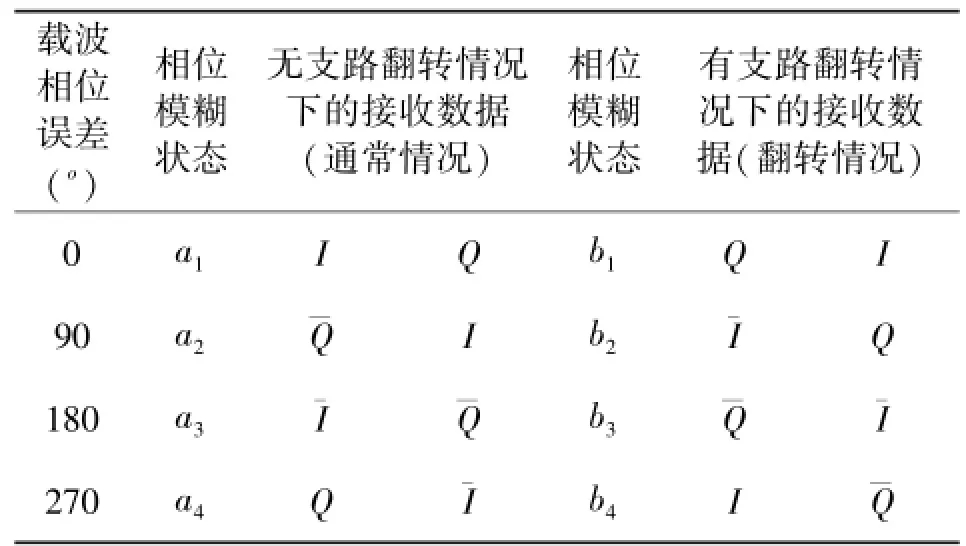
表2 相位模糊中发送和接收数据间的关系Table2 Relations between transmission and reception data in phase-ambiguity

注:在无支路翻转、00相位误差情况下,通过解调恢复的接收端同相支路I和正交支路Q的二进制数据与发送端相同,符号上的横杠表示取该符号的反码。

从表1中可看出,相位模糊共有8种情况。a1状态下接收端的数据与发送端一致,b1状态下接收端的数据可由a1状态下接收端的数据经IQ路比特交换产生,b2、b4、a3状态下接收端的数据可由a1状态下接收端的数据分别经I路比特取反、Q路比特取反、IQ路比特取反产生;a2、a4、b3状态下接收端的数据可由b1状态下接收端的数据分别经I路比特取反、Q路比特取反、IQ路比特取反产生。

以下将对IQ路比特交换、I路比特取反、Q路比特取反和IQ路比特取反共4种情况下的采样校验元变化情况、译码后信息变化情况分别进行讨论。

2 采样校验元在相位模糊下的变化情况

设卷积码接收序列为c,基本校验矩阵为h,由卷积码的性质有c·hT=0成立,因QPSK调制方式中1个码元含2个比特,令基本校验矩阵h经奇数位抽取、偶数位抽取分别得到的2个校验元为采样校验元,分别记为h1、h2。

2.1 基本校验矩阵对于相位模糊的透明性分析

在校验过程中,序列c参与校验的比特数与基本校验矩阵h的维数相同,因h由0和1构成,h中0的位置对应的序列c中的比特,实质上对校验没有贡献,即序列c中实质参与校验的比特个数与h的抽头数相同。由表1可知,(2,1,6)卷积码及其各码率删除卷积码的基本校验矩阵抽头数均为偶数,即序列c实质参与校验的各比特模2加的结果为0,故序列c中实质参与校验的0比特个数和1比特个数也均为偶数。

从通常情况的a1状态或翻转情况的b1状态来看,在1800相位模糊下,IQ路比特取反后实质参与校验的0比特个数和1比特个数仍为偶数,若基本校验矩阵保持不变,实质参与校验的各比特模2加的结果仍为0,满足校验关系,故基本校验矩阵保持不变,也即是对1800相位模糊是透明的;在900或2700相位模糊下,IQ路比特交换后任一路比特取反将导致基本校验矩阵发生变化,故基本校验矩阵对900或2700相位模糊均不透明。

2.2 IQ路比特交换(IQ→QI)对采样校验元的影响

IQ路比特交换,相当于仅存在支路翻转情况,无载波相位误差,只需将基本校验矩阵相邻的2个比特进行交换,就可得变换后的基本校验矩阵,即原采样校验元相互交换可产生变换后的采样校验元,原采样校验元为(h1,h2),变换后采样校验元为(h2,h1),卷积码码率、抽头数和采样校验元如表3所示。

表3 卷积码码率、抽头数和采样校验元关系Table 3 Relations among convolution code bit rate,tap numbers and sample check codes

由表3可看出,3/4、4/5、5/6三种码率的删余卷积码在通常情况下,其采样校验元的抽头数均为偶数,由透明性分析可知,I路比特取反,若采样校验元不变,将不会影响到I支路的校验,故采样校验元对IQ→Q变换是透明的。由于采样校验元不变,故无法通过采样校验元来判断是否存在I路比特取反的情况。

1/2、2/3、6/7、7/8四种码率的删余卷积码的采样校验元的抽头数均为奇数,I路比特取反,将使I支路的校验结果取反(I支路的校验结果将由0变为1或1变为0),Q路比特不变,将不会影响Q支路的校验结果(仍为1或0),最终导致基本校验矩阵h的校验结果取反(由0变为1),因此基本校验矩阵、采样校验元将发生变化,故采样校验元对IQ→Q变换是不透明的,因此可通过采样校验元的变化来判断是否存在I路比特取反的情况。

对于n-1/n码,令,由卷积码的性质可知,φ1、φ2也为卷积码的校验矩阵,通过以上分析可得,校验矩阵φ1、φ2的校验结果均为1,故将φ1与φ2作模2加运算可产生变换后的基本校验矩阵φ,基本校验矩阵φ对I路比特取反后的数据进行校验的结果均将为0。卷积码码率、抽头数和采样校验元如表4所示。

表4 卷积码码率、抽头数和采样校验元关系Table 4 Relations among convolution code bit rate,tap numbers and sample check codes

以2/3码为例,其基本校验矩阵、采样校验元、子校验元如表5所示。

表5 2/3码率卷积码的基本校验矩阵、采样校验元、子校验元关系Table5 Relations among basic check matrix,sample check codes and sub-check codes of 2/3 convolution code

I路比特取反后,变换后基本校验矩阵φ是基本校验矩阵h与h移位3比特后模2加的结果,故其变换后子校验元是变换前子校验元ε与ε延迟一位后模2加的结果,相当于各子校验元进行了差分译码,因此只要对I路比特取反情况下的子校验元进行0初态的差分编码即可恢复标准子校验元。

分析过程类似于I路比特取反,3/4、4/5、5/6三种码率的删除卷积码的采样校验元将不会发生变化,对IQ→I变换是透明的,无法通过采样校验元来判断是否存在Q路比特取反的情况。

1/2、2/3、6/7、7/8四种码率的删除卷积码的采样校验元将发生变化,因采样校验元的抽头数均为奇数,I路比特取反与Q路比特取反对校验结果的影响相似,对于n-1/n码,基本校验矩阵h与h移位n比特后模2加的结果,就是变换后的基本校验矩阵φ,故Q路比特取反与I路比特取反的采样校验元相同,卷积码码率、抽头数和采样校验元关系如表6所示。

表6 卷积码码率、抽头数和采样校验元关系Table 6 Relations among convolution code bit rate,tap numbers and sample check codes

2.5 IQ路比特取反(IQ→)

由基本校验矩阵的透明性分析可知,各种码率卷积码的抽头数都为偶数,其基本校验矩阵、采样校验元对1800相位模糊均是透明的,故采样校验元对于IQ→变换将保持不变。

3 译码后信息在相位模糊下的变化情况

3/4、4/5、5/6三种码率卷积码的采样校验元对于I路比特取反、Q路比特取反、IQ路比特取反均保持不变,无法通过采样校验元来判断相位模糊情况,可分析以上3种情况对卷积码译码后信息的影响,以便正确还原卷积码译码信息,而后对译码后信息开展进一步的后续检验。

令信息序列为m,卷积码生成多项式为G,卷积码接收序列为c,I路比特取反后卷积码序列变为u,相当于在序列c上增加了一层底码序列t,即u=c⊕t,其中序列t=(10101010…),满足以下关系:

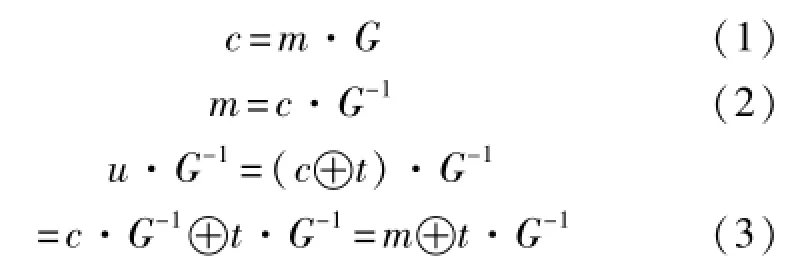
式(2)中序列c乘以G-1相当于对序列c进行译码,式(3)中序列u乘以G-1相当于对变换后序列u进行译码,将变换后序列u的译码结果u·G-1与t·G-1进行模2加,就能还原出信息序列m。

以3/4卷积码为例,根据文献[5]可求出生成多项式矩阵,由不变因子分解定理[6]可求出生成多项式逆矩阵,结果如下:

将序列t分成4路,以多项式形式表示,即:

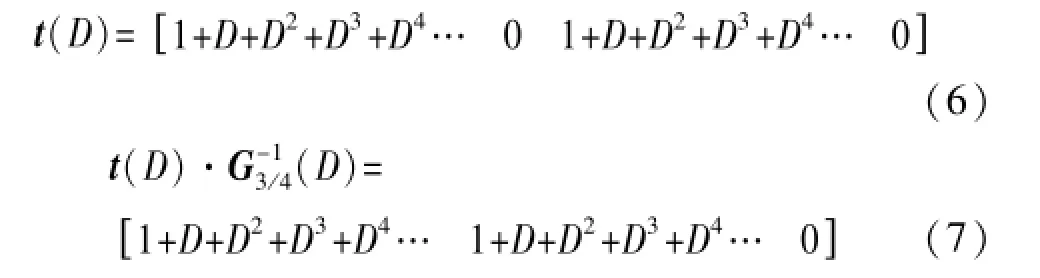
故t·G-1=(110110110110…),从式(5)的生成多项式逆矩阵(D)也可看出,其第1列中的第1行和第3行共计9个抽头,第2列中的第1行和第3行共计9个抽头,第3列中的第1行和第3行共计6个抽头,故第1列、第2列译码后信息为1,第3列译码后信息为0,相当于存在"110"的底码,即对译码后信息加上″110″的底码,就能得到正确的信息序列。同理可获取4/5、5/6码率的底码序列。

3/4、4/5、5/6码率卷积码的序列t和译码后底码序列如表7所示。

表7 3/4、4/5、5/6码率卷积码的序列t和译码后底码序列Table 7 Original sequences and sequences after decoding of 3/4,4/5 and 5/6 convolution codes

Q路比特取反变换相当于在序列u上增加一层t=(01010101…)的底码序列,3/4、4/5、5/6码率卷积码的序列t和译码后底码序列如表8所示。

表8 3/4、4/5、5/6码率卷积码的序列t和译码后底码序列Table 8 Original sequences and sequences after decoding of 3/4,4/5 and 5/6 convolution codes

IQ路比特取反变换相当于在序列u上增加一层t=(11111111…)的底码序列,3/4、4/5、5/6码率卷积码的译码后底码序列均为(11111111…)。

4 仿真测试及结论

对接收的卷积码通过文献[7]求取基本校验矩阵,再经间隔抽取获得采样校验元,通过采样校验元判断相位模糊情况。

例如一标准2/3删除卷积码序列不存在支路翻转、仅有900相位误差,即IQ→,相当于先进行支路翻转、再进行I路比特取反,即IQ→QI→(I路比特取反即为第一路比特取反,故此时对QI进行第一路比特取反的结果为I),对接收的卷积码求取基本校验矩阵为h=(111110111011000001111101),采样校验元h1=(111111000110),h2= (110101001111),与表3、表4、表6对比可看出存在支路翻转,但无法判断是I路比特取反,还是Q路比特取反,需进行进一步的分析,但这已经减少了人工判断的工作量,从全部8种可能降低为2种可能,即排除了6种错误可能。

例如一标准3/4删除卷积码序列存在支路翻转和1800相位误差,即IQ→,相当于先进行支路翻转,再进行IQ路比特取反,即IQ→QI→,对接收的卷积码求取基本校验矩阵为h= (1111111001011100100101111100),采样校验元h1=(11110010100110),h2=(11101110011110)。与表3、表4对比可看出存在支路翻转,但无法判断是无支路取反、I路比特取反、Q路比特取反还是IQ路比特取反,需将译码后信息与表7、表8中各种可能的译码后底码序列进行模2加,再开展进一步的分析判证,通过这项工作已将全部8种可能降低为4种可能,即排除了4种错误可能。

对标准(2,1,6)卷积码及其各码率删余卷积码有以下结论:

①对于3/4、4/5、5/6三种码率,可通过采样校验元判断是否存在IQ路比特交换,但对无支路取反、I路比特取反,IQ路比特取反或Q路比特取反的情况无法识别,需将译码后信息与各种可能的译码后底码序列进行模2加,再分别对各个结果的正确性开展进一步的分析判断,最终确定相位模糊情况。

②对于1/2、2/3、6/7、7/8四种码率,可通过采样校验元或子校验元判断是否存在IQ路比特交换,能正确区分两类支路取反情况(无支路取反、IQ路比特取反为一类,I路比特取反、Q路比特取反为一类),但对每一类的具体取反情况,需将译码后信息与可能的译码后底码序列进行模2加,再开展进一步的分析判断。

5 结 语

文中重点研究了(2,1,6)卷积码及其各码率删余卷积码的采样校验元与相位模糊间的关系,对于(2,1,3)、(2,1,7)、(2,1,8)等各种码率的标准卷积码与删余卷积码均可通过基于采样校验元的识别方法进行相位模糊分析,证明该方法对于标准卷积码具有普遍适用性。该方法相比于通过遍历所有可能的相位模糊情况、对每种可能情况开展后续判证的传统方法,充分利用了信道纠错编码的约束关系,挖掘了更多的有用信息,降低了相位模糊情况的可能数量,继而在可能情况的范围内开展后续分析,减少了人工观察判断的工作量,提高了工作效率。

[1] 张梦龙,胡艳君.基于FPGA的卷积码的编/译码器实现[J].通信技术,2011,44(05):1-5.

ZHANG Meng-Long,HU Yan-Jun.Encoder and Decoder Design for Convolutional code based on FPGA[J]. Communication Technology,2011,44(5):1-5.

[2] 曹志刚,钱亚生.现代通信原理[M].北京:清华大学出版社,1992.

CAO Zhi-Gang,QIAN Ya-Sheng.Principles of Modern Communications[M].Beijing:TsinghuaUniversity press,1992.

[3] TSUJI Y.Phase Ambiguity Resolution in a 4-Phase PSK Modulation System with Forward Error Correcting Convolutional Codes[J].Comsat Technical Review,1976,6 (02):357-377.

[4] CACCIAMANI E,WOLEJSZA C.Phase-Ambiguity Resolution in a Four-Phase PSK Communications System [J].IEEE Trans.on Communication Technology,1971, 19(06):1200-1210.

[5] 陆佩忠,沈利.删除卷积码的盲识别[J].中国科学E辑信息科学,2005,32(02):173-185.

LU Pei-Zhong,SHEN Li.Blind Recogntition of Punctured Convolutional Codes[J].SCIENCE IN CHINA Ser.E Information Sciences,2005,32(2).

[6] 刘玉君.非系统卷积码信息恢复算法的研究[J].信息工程大学学报,2008,8(02):195-197.

LIU Yu-Jun.Studies on Algorithms for Information Recovery of Nonsystematic Convolution Codes[J].Journal of Information Engineering University,2008,8(2):195-197.

[7] 朱联祥,王思义.基于校验矩阵的卷积码盲识别技术研究[J].电视技术,2014,38(01):140-144.

ZHU Lian-xiang,WANG Si-yi.Blind Identification of Convolution Code based on Parity Check Matrix[J].Video Engineering,2014,38(1):140-144.

TU Sun(1982-),male,graduate student, majoring in satellite communication signal processing and channel coding recognition.

高 勇(1969—),男,博士,教授,主要研究方向为阵列信号处理、电子侦察、通信抗干扰技术、信号分析、声信号处理、嵌入式系统开发。

GAO Yong(1969-),male,Ph.D.,professor,mainly interested in array signal processing,electronic reconnaissance, anti-interference technology of communication,signal analysis, acoustic signal processing,development of embedded system.

Standard Convolution Code in Condition of QPSK Phase-Ambiguity

TU Sun1,2,GAO Yong1
(1.College of Electronics and Information Engineering,Sichuan University,Chengdu Sichuan 610065,China; 2.Unit 78009 of PLA,Chengdu Sichuan 610066,China)

In digital phase modulation system,there always exists carrier phase-ambiguity in the process of coherent demodulation.Traditional method traverses all the possible situations,with fuzzy processing and subsequent judgment to check correctness,and this is low in efficiency.Aiming at 8 kinds of phase-ambiguity in QPSK demodulation,restriction relations of convolutional code are used to study the changes of sample check codes of standard(2,1,m)codes and punctured codes,and the impact of phase-ambiguity on messages after decoding and finally a method of phase-ambiguity based on sample check code's detection is proposed.The method can effectively reduce the probable numbers of phase-ambiguity,and greatly improve the working efficiency of manual judgment.

convolutional code;phase-ambiguity;sample check code

TN911

A

1002-0802(2014)09-1004-06

10.3969/j.issn.1002-0802.2014.09.006

涂 榫(1982—),男,硕士研究生,主要研究方向为卫星通信信号处理和信道编码识别;

2014-07-02;

2014-08-12 Received date：2014-07-02;Revised date：2014-08-12