基于免疫进化细菌觅食算法的多目标无功优化
李 莹,简献忠
(上海理工大学 电气工程系,上海 2 00093)
基于免疫进化细菌觅食算法的多目标无功优化
李 莹,简献忠
(上海理工大学 电气工程系,上海 2 00093)
为了更好地解决电力系统多目标无功优化问题,分析了当前多目标无功优化算法存在的缺陷,提出了一种基于免疫进化的改进多目标细菌觅食优化算法。该算法求得的Pareto最优解分布均匀,收敛性和鲁棒性好。IEEE14,IEEE30节点测试系统的算例结果表明所提的算法在多目标无功优化中具有良好的效果,为各目标之间的权衡分析提供了有效工具,是一种求解多目标无功优化问题的有效方法。
无功优化;多目标;免疫进化;细菌觅食优化算法;非支配排序
0 引言
当前随着电力系统规模的不断扩大,无功优化涉及的目标越来越多[1~3],然而各个目标之间存在竞争关系,彼此矛盾。传统的多目标无功优化方法将多目标问题转化为单目标再求解[4~6],这类方法存在明显的缺点:每次计算彼此独立,结果可能出现不一致的情况,且优化过程中考虑的各因素在总目标中所占权重的改变将影响整个目标系统无功的优化结果。因此,本文将基于精英选择法的Pareto最优前沿[7]引入寻优机制中,利用非支配排序和拥挤距离排序对种群进行选择更新,且输出一组Pareto非支配解集[8],为不同的应用场合及需求提供选择。
目前应用于无功优化的智能算法很多,并取得了一些研究成果[9~11],但是基于 Pareto最优前沿的多目标细菌觅食优化算法的研究文献尚未见报道,因此,本文提出一种基于免疫进化的改进多目标细菌觅食优化算法 (IA-IBFO),并将此算法应用于多目标无功优化问题,最终仿真结果表明,本文算法不仅能够保持Pareto最优解的多样性,同时还具有很好的收敛性能。
1 无功优化模型与Pareto最优解概念
1.1 多目标无功优化的数学模型
本文选择系统有功网损最小为经济性指标,电压偏移量最小以及电压安全稳定裕度最大为技术性指标,无功优化的多目标函数表达式如下[12]:
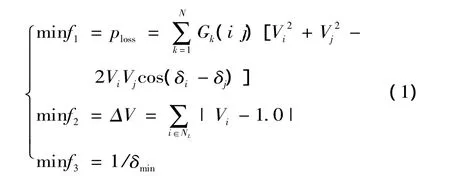
式中:f1为系统网损;f2为电压偏差;f3为电压稳定裕度;N为系统支路数;Gk(i,j)为线路k的电导;Vi,Vj,δi,δj为支路k两端节点电压幅值和相角;以系统收敛潮流雅可比矩阵的最小奇异值δmin作为系统静态电压稳定裕度的指标,为了使各目标函数具有统一的最小化形式,对δmin取倒数,将静态电压稳定裕度最大转化为最小化函数形式。
1.2 等式约束

等式约束是指有功功率与无功功率保持平衡的条件,即功率平衡方程。式中:Pi,Qi分别为给定的节点i的有功和无功;Bij为节点i,j之间的电纳值;N0为除平衡节点外的总节点数。
1.3 不等式约束
不等式约束条件指控制变量的约束条件与状态变量的约束条件。
(1)控制变量约束

式中:Ng为可调发电机的节点数;NT为可调变压器的节点数;Nc为无功补偿装置的节点数;Vgi为发电机的机端电压;Ti为可调变压器变比,Qci为无功补偿装置容量。
(2)状态变量约束

式中:Qgi为发电机无功出力;Vdi为PQ节点电压。
1.4 Pareto最优解的基本概念
(1)Pareto支配关系。对于两个决策变量u和v,且u∈S,v∈S,若满足:

则称决策变量u支配v,记为u≻v。此时称u为非支配的,v为被支配的。
(2)Pareto最优解。对于多目标优化问题的一个可行解x*∈S,当且仅当S中不存在x,使x≻x*,即x*是可行域S的非支配个体,则称x*为多目标优化问题的Pareto最优解,所有Pareto最优解构成Pareto最优解集,也就是全局最优解集。
2 基于免疫进化的改进多目标细菌觅食优化算法及其在无功优化中的应用
2.1 改进的细菌觅食算法
细菌觅食优化算法 (Bacterial Foraging Optimization,BFO)是Passina于2002年基于细菌觅食行为而提出的一种仿生随机搜索算法[13],该算法通过群体细菌之间的竞争和协作,实现搜索的优化,在BFO算法中,最核心的一个步骤就是趋化操作,趋化算子根据适应度调节游动方向,通过随机游动来搜索全局最优解,从而确保了细菌的局部搜索能力,但由于细菌没有充分利用其他细菌个体的信息,使得收敛速度较慢。为此,本文将赋予细菌以灵敏度来感知个体极值和全局极值的差异,使得细菌自适应调节游动步长,以适应环境。具体步骤改进如下:
(1)产生单位向量φ(i),细菌执行翻转操作。
(2)改善细菌种群位置。细菌个体按照灵敏度进行群游,当适应度不再增强时,则操作结束,灵敏度定义为:
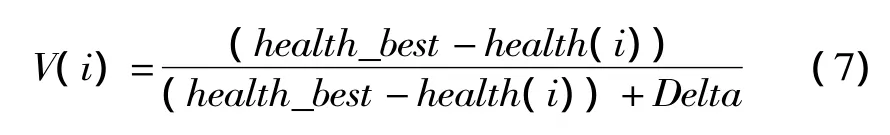
其中,health_best表示细菌种群历史最好位置,health(i)表示第i个细菌当前位置,Delta定义为灵敏度算子,其大小由适应度函数的变化范围决定,在此取值为6 000;式 (8)为细菌群游公式:

式中:P(i,j,k,l)表示第i个细菌的空间位置向量,其中j表示第j代趋化循环,k表示第k代繁殖循环,l表示第l代迁移循环;φ(i)表示群游选定的方向。
(3)将复制操作与驱散操作合并为以适应度作为判断条件的驱散操作,设细菌个体的适应度为AdaptVi,菌群的平均适应度为MeanAdapt,如果AdaptVi>MeanAdapt,则对该细菌个体执行驱散操作。由于多目标优化有多个优化指标可以作为适应度的判断条件,本文选取如下方案作为适应度的判断条件,去菌群的平均适应度为每个个体极值的平均值,即:
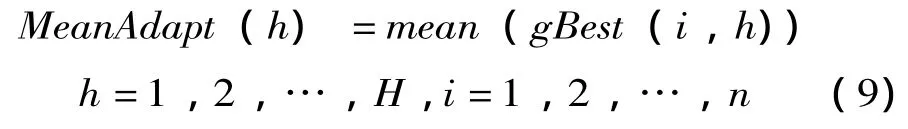
其中,H是目标函数的个数,n是菌群数目,mean(gBest(i,h))表示n个细菌个体极值的平均值。
2.2 应用于多目标无功优化的免疫细菌觅食算法
(1)初始群体的生存和编码方式
本文编码方案采用实数和整数混合的方式。控制变量中,PV节点发电机机端电压采用实数编码,并联电容投运组数、有载调压变压器主接头档位为整数编码。则控制变量编码格式为:

式中:UGi,Ci,Ti分别为某PV节点发电机机端电压、并联电容投运组和有载调压变压器主接头档位;NC,NT分别为PV节点并联电容补偿节点总数和有载调压变压器组数。
(2)非支配排序
在选择运算之前,用擂台赛法则构造非支配解集。其基本思路是:在每一轮比较时,从构造集中选出一个个体出任擂主,由擂主与构造集中其他个体进行比较,败者被淘汰出局,胜者成为新的擂主,并继续该轮比较。一轮比较后,最后的擂主个体即为非支配个体,将其保存在外部精英集中。该算法的时间复杂度优于改进的非支配遗传算法[14]。
(3)拥挤度算子
为了保持个体的多样性、防止个体在局部堆积,引入拥挤度距离这一概念。拥挤度是指种群中给定个体周围的个体密度,计算步骤为:①对个体初始化距离,令L[i]d=0;②对个体按第m个目标函数值升序排列;③使得排序边缘上的个体具有选择优势,给定一个大数L[0]d=L[l]d=M;④对排序中间的个体,求拥挤距离:L[i]d=L[i]d+(L[i+1]m-L[i-1]m)(L[i]m为第i个个体的第m目标函数);⑤对不同的目标函数,重复步骤②~④。
(4)选择运算
选择过程使优化朝着Pareto最优解的方向进行并使解均匀散布。经过排序,非支配个体已保存在精英集中,对精英集中的个体按照拥挤距离大小再次排序,取拥挤距离相对大的个体保留,即周围较不拥挤的个体,淘汰掉拥挤距离较小的个体,这将使Pareto最优解集具有多样性,并且均匀分布。
(5)精英集的克隆选择
本文借鉴免疫算法中的克隆选择思想[15],并将其引入Pareto最优解集中,通过克隆、高频变异和随机交叉操作来增加Pareto最优解的多样性,以及提高算法的收敛精度。
①在每代产生的非支配集中,选择拥挤度距离大的粒子进行自我复制,产生克隆群体Nc。
②对Nc进行高频变异,随后进行随机交叉,其中,高频变异按照公式 (11)进行,β是高频变异概率,按照公式 (12)计算,适应值越小的个体,变异的概率越大,搜索的空间越宽。其中fit为个体的适应值,m为目标函数的个数。
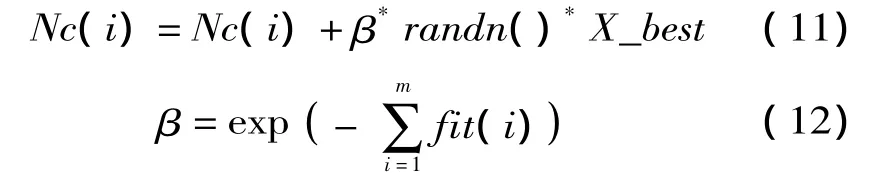
③对NC群体进行随机交叉,产生s个粒子后代,作为免疫细胞注入Nc群体。交叉采用公式(13)进行,其中a,b,c,d为克隆群体的互不相同的随机粒子。
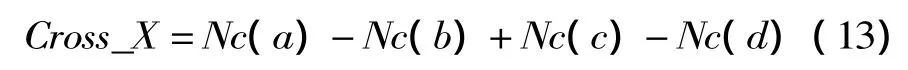
④采用免疫算法的克隆、变异、交叉策略形成Nc+s个新种群,对其适应值进行比较后产生非支配解集,该解集与当代非支配解集合并产生更新的Pareto最优解集,加入精英集中。
由步骤 (1)~(5)可得基于IA-IBFO的多目标无功优化流程图如图1所示。
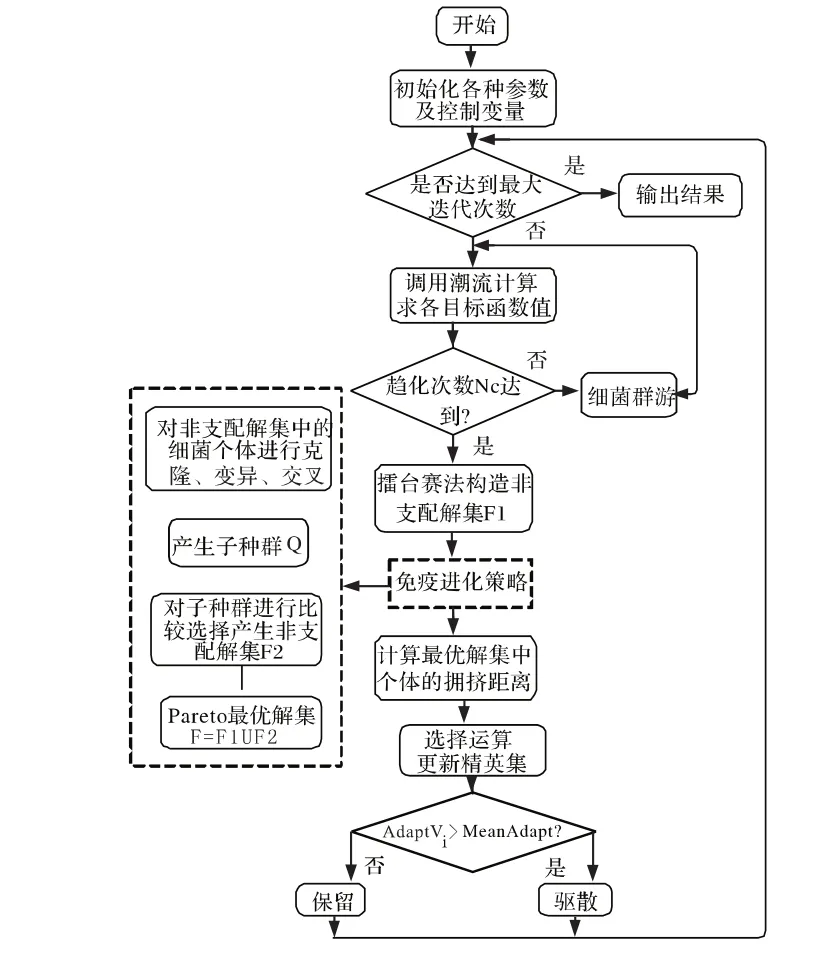
图1 基于IA-IBFO算法的多目标无功优化流程
3 算例分析
本文使用Matlab进行无功优化仿真计算,分别对IEEE14节点和IEEE30节点系统进行仿真来验证本文所提算法的优化效果。算法中相关的参数选取为:种群规模n=100,精英集规模F=20,迭代次数itermax=100。
3.1 IEEE14节点优化结果
IEEE14系统共有14个节点,20条支路,5台发电机,3台可调变压器以及1个并联补偿电容器节点,系统节点参数和支路参数参见文献[16]。为了便于分析说明,本算例只考虑有功网损和电压稳定裕度两个指标,仿真测试结果如图2所示。
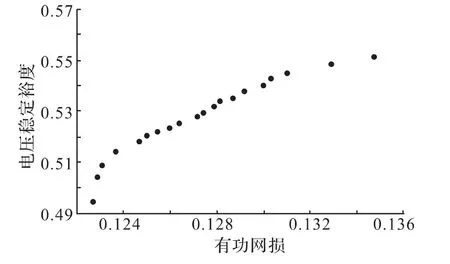
图2 基于IA-IBFO算法的无功优化Pareto前沿
图2显示了某次计算求得的1组Pareto解的分布,从图可以看出有功网损与电压稳定裕度这两个目标函数相互矛盾,最优解集分布均匀,具有较好的多样性,能给用户提供了多样化的选择。
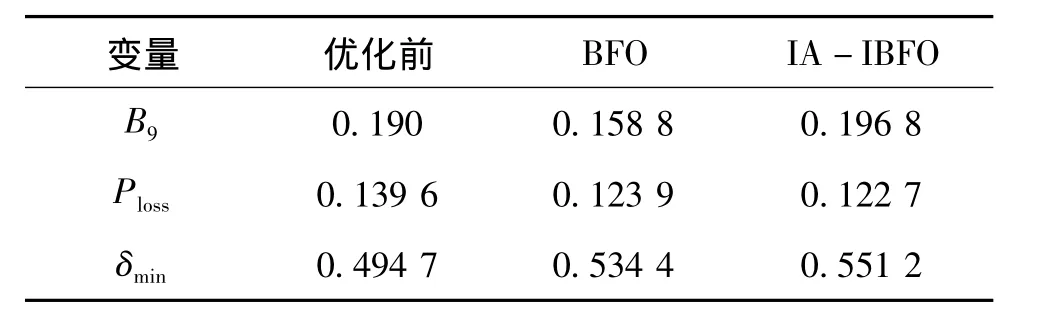
表1给出了IA-IBFO算法与标准BFO算法分别运行30次无功优化所得最优解。
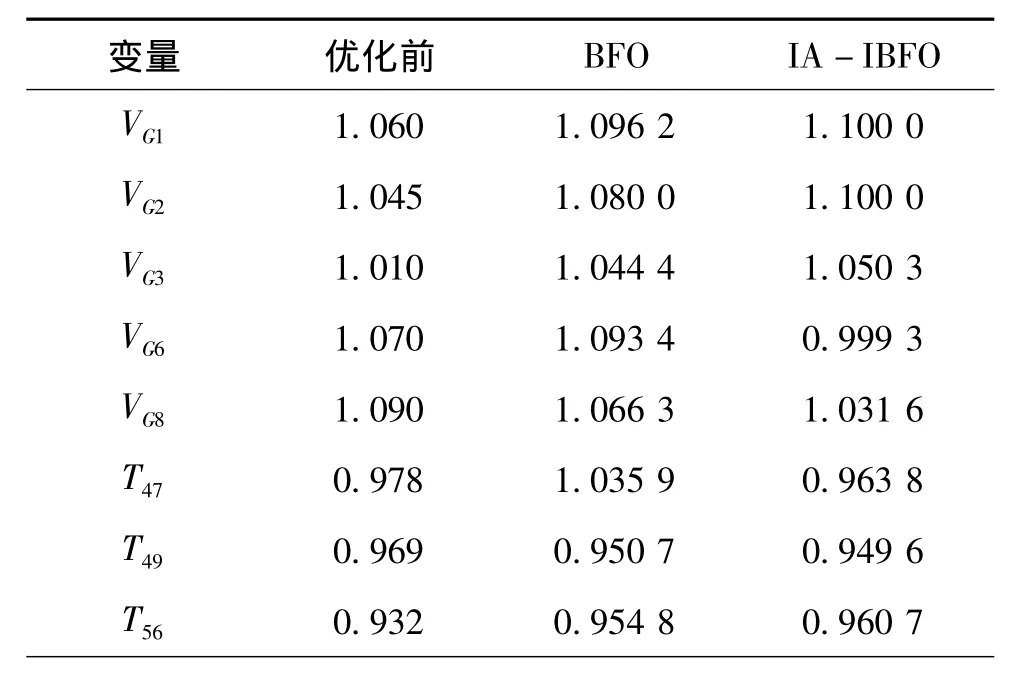
表1 不同算法优化结果比较
续表
由表1知,IA-IBFO优化后系统的网损降低12.11%,BFO优化后网损降低11.25%;IAIBFO优化后的电压稳定裕度也优于BFO。由此可见,IA-IBFO算法在寻优过程中能更好地发现全局最优解。
IA-IBFO和BFO两种算法的有功网损和电压稳定裕度的收敛曲线图分别如图3、图4所示,由图可以看出本文所提算法无论在收敛速度上还是优化效果上都优于BFO。

图3 BFO和IA-IBFO的有功网损收敛特性曲线图

图4 BFO和IA-IBFO的电压稳定裕度收敛特性曲线图
3.2 IEEE30节点优化结果
IEEE30系统共有30个节点,41条支路,6台发电机,4台可调变压器以及2个并联补偿电容器节点,系统节点参数和支路参数参见文献[15]。运用IA-IBFO算法对系统进行无功优化,仿真结果如图5所示。由图可以看出该算法无功优化所得Pareto最优前沿分布比较均匀,可以反映出IA-IBFO算法在寻优过程中能更好地保持种群多样性,保证算法在全局区域能有更好的搜索能力。
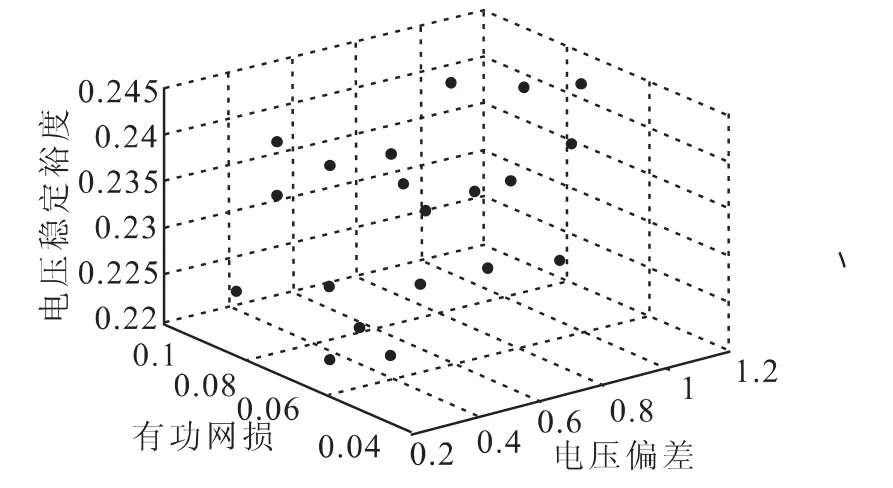
图5 IA-IBFO的Pareto前沿
表2给出了IA-IBFO与BFO的性能对比,由IA-IBFO算法得到的有功网损,电压偏差及电压稳定裕度均优于BFO所得的结果。

表2 不同算法优化结果比较
4 结论
本文提出一种基于免疫进化的改进多目标细菌觅食优化算法,并将其首次应用于多目标无功优化。仿真结果表明,该算法能较快地收敛到全局最优解,并且Pareto最优解集分布均匀,具有较好的多样性,决策者可根据实际系统的要求进行最优解的选择,避免了对多目标进行加权求解的盲目性,体现了多目标优化的工程实际意义,是一种求解多目标无功优化的好方法。当前随着电力系统规模的扩大,无功优化时需要考虑的因素必将越来越多,如何进行电力市场下的无功优化的建模,国内外的学者正在积极探索,相信IA-IBFO可提供一个较好的算法支持。
[1] Stephen D S,Somasundaram P.Solution for multi-objective reactive power optimization using fuzzy guided tabu search[J].Arabian Journal for Science and Engineering,2012,37(8):2231-2241.
[2] Rayudu K,Jayalaxmi A,Yesuratnam G,et al.Multi objective comparison of GA and LP techniques for generator reactive power optimization[C].Power India Conference,2012 IEEE Fifth.IEEE,2012:1-5.
[3] Singh H,Srivastava L.Multi-objective reactive power management using differential evolution[C].Power Electronics(IICPE),2012 IEEE 5th International Conference on.IEEE,2012:1-6.
[4]王玉荣,万秋兰,陈昊.基于模糊聚类和学习自动机的多目 标 无 功 优 化 [J].电 网 技 术,2012,36(7):224-230.
[5]陈得宇,张仁忠,沈继红,等.基于适应性权重遗传算法的多目标无功优化研究[J].电力系统保护与控制,2010,38(6):1-7.
[6]马立新,王守征,吕新慧,等.电力系统无功优化的反向优化差分进化算法 [J].控制工程,2010,17(6):803-806.
[7]李鑫滨,朱庆军.一种改进粒子群优化算法在多目标无功优化中的应用 [J].电工技术学报,2010,25(7):137-143.
[8] Kalyanmoy Deb,Amrit Pratap,Sameer Agarwal,et al.A fast and elitist multi-objective genetic algorithm:NSGA-II[J].Evolutionary Computation,IEEE Transactions on,2002,6(2):182-197.
[9] Abido M A.A niched Pareto genetic algorithm for multiobjective environmental/economic dispatch[J].International Journal of Electrical Power& Energy Systems,2003,25(2):97-105.
[10]李鸿鑫,李银红,李智欢.多目标进化算法求解无功优化问题的比较与评估 [J].电网技术,2013,37(6):1651-1658.
[11] Zhang X,Chen W,Dai C,et al.Dynamic multi-group self-adaptive differential evolution algorithm for reactive power optimization [J].International Journal of Electrical Power& Energy Systems,2010,32:351-357.
[12]李如琦,李芝荣,王维志,等.基于差分策略的多目标电力系统无功优化 [J].电网技术,2012,36(12):170-175.
[13] Passina K M.Biomimicry of bacterial foraging for distributed optimization and control[J].Control Systems Magazine,IEEE,2002,22(3):52-67.
[14]郑金华,蒋浩,邝达,等.用擂台赛法则构造多目标Pareto最优解集的方法 [J].软件学报,2007,6(18):1287-1297.
[15]Castro L N,Zuben F J.Artificial immune system:Part I:basic theory and applications[R].Campinas,Brazil:State University of Campinas,School of Computing and E-lectrical Engineering,1999.
[16]张伯明,陈寿孙,严正.高等电力网络分析 [M].(第2版).北京:清华大学出版社,2007.
Bacterial Foraging Optimization Algorithm Based on Immune Algorithm for Multi-Objective Reactive Power Optimization
Li Ying,Jian Xianzhong
(Department of Electrical Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)
In order to solve the problem of multi-objective reactive power optimization,firstly the defects of current algorithms are analyzed,then an improved multi-objective bacterial foraging optimization algorithm based on immune algorithm technique is proposed.It can obtain uniformly distributed Pareto-optimal solutions and has good convergence and excellent robustness.Finally this method is applied to IEEE14-bus and IEEE30-bus testing system.The results show that the proposed method can obtain good results for multi-objective reactive power optimization,which provides an effective tool for measuring the performance of different objective functions.Thus it should be a new method for multi-objective reactive power optimization in power systems.
reactive power optimization;multi-objective;immune algorithm;bacterial foraging optimization algorithm;non-dominated sorting
TM714.3;TP301.6
A
10.3969/j.issn.1672-0792.2014.04.002
2013-11-28。
上海市自然科学基金资助项目 (12ZR1420800)。
李莹 (1987-),女,硕士研究生,研究方向为电能质量优化与分析,E-mail:727145259@qq.com。

