时变混合系统的在线FastICA算法*

陈海平,张 杭,路 威,张 江

(1.解放军理工大学通信工程学院,江苏南京210007;2.总参第63研究所,江苏南京210007)

时变混合系统的在线FastICA算法*

陈海平1,张 杭1,路 威1,张 江2

(1.解放军理工大学通信工程学院,江苏南京210007;2.总参第63研究所,江苏南京210007)

现有的多数盲源分离(BSS,Blind Source Separation)算法都是假设混合系统是时不变的,然而在实际的通信系统中混合系统常常是时变的。传统的快速不动点(FastICA)算法具有快速收敛的优点,但是不能直接用于处理混合系统时变的盲源分离问题。为了提高盲源分离算法的收敛速度和对时变混合系统的跟踪性能,改进了传统FastICA算法,将混合信号分段,在各段样本中估计峭度并采用批处理的方法进行分离。仿真实验表明,改进后的FastICA算法能在时变环境中跟踪混合系统的时变,并能有效地抗多音干扰。

盲源分离 时变 快速不动点算法 收敛速度 在线算法

0 引 言

盲源分离是在源信号和信道未知的条件下,根据源的独立性,仅利用传感器输出的混合信号来实现源信号的分离的过程[1],是信号处理领域和神经网络领域的研究热点之一。在无线通信系统中,由于信号源或接收端运动等因素影响,无线信道往往是时变的。因此,研究时变混合盲源分离算法具有重要的意义。

然而,大部分盲分离算法都是在假设混合系统时不变的条件下得到的,如特征矩阵联合近似对角化(JADE)算法[2]、快速不动点算法(FastICA)及其改进算法[3-4]等,这些算法无法实时跟踪混合系统的时变,因此不能用来解决时变混合盲分离问题。

根据对数据处理方式的不同,盲分离算法可分为在线算法(或自适应算法)和批处理算法。通过在线算法估计的分离矩阵既与前一时刻估计的分离矩阵有关,还与当前时刻的观测信号有关,因此,在线算法具有跟踪时变混合系统的能力。而批处理算法则不具备这种能力,如果在时变混合系统中采用基于混合系统时不变假设的批处理算法,恢复的源信号往往是错误的。很多经典的盲源分离算法可用于解决时变混合的盲源分离问题,如基于独立性的等变自适应(EASI,Equivariant Adaptive Separation via Independence)盲源分离算法,非线性主元分析(NPCA,Nonlinear Principal Component Analysis)算法等,但是这些算法收敛速度慢,当混合信道变化很快时无法跟踪信道变化。

为了提高算法收敛速度和对时变混合系统的跟踪性能,文中将借鉴传统FastICA算法的快速收敛、迭代简洁等优点,但是由于FastICA算法属于批处理算法,它是以四阶累积量(即峭度)作为非高斯性的度量,基于不动点迭代推导而来的,无法跟踪混合系统的时变。因此,文中考虑改进FastICA算法,使之能够跟踪混合系统的时变,实现在时变混合条件下的盲源分离。考虑到峭度作为非高斯性的度量,不能用单个样点值估计,必须以一定数量的采样点才能比较准确地估计出来,因此,文中将采用分段批处理的方法改进FastICA算法,使之既保持FastICA算法快速收敛和迭代形式简洁的优点,又能跟踪时变混合系统。

1 问题描述

1.1 时变混合盲源分离

时变混合盲源分离的模型如图1所示。

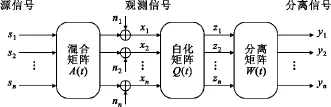
图1 时变混合盲源分离模型Fig.1 Time-varying BSS model

假设具有n个相互统计独立分量的源信号矢量s(t)=(s1(t),s2(t),…,sn(t))T中,至多只有一个分量是高斯的,其中t=1,2,…,L表示采样时刻,L为采样长度。经过时变系统混合后,得到观测信号(或混合信号)矢量x(t)=(x1(t),x2(t),…,xm(t))T,其中m为观测信号的分量个数,本文考虑m=n(即适定混合)的情况。混合过程可由下式表示:

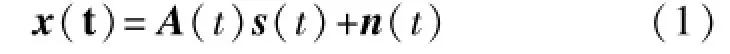
其中n(t)=(n1,n2,…,nn)T是系统中的噪声矢量, A(t)是时变混合矩阵。

盲源分离的主要任务是使观测信号x(t)= (x1(t),x2(t),…,xm(t))T通过盲分离算法分离后,得到的分离信号y(t)=(y1(t),y2(t),…,yn(t))T的各个分量尽可能统计独立。

对观测数据进行白化预处理有助于简化对数据的后续分离,在时变环境中,一般采用在线白化的方法来实现观测信号的白化预处理,白化信号z(t)= (z1(t),z2(t),…,zn(t))T可由以下迭代公式得到:

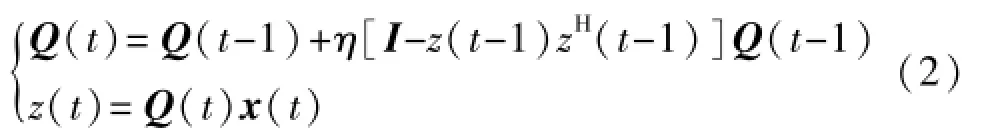
其中Q(t)为t时刻的白化矩阵,η为迭代步长,I为单位矩阵。然后为白化信号寻找一个合适的分离矩阵W(t),使得白化信号z(t)经过W(t)后得到各分量尽可能独立的分离信号y(t)=(y1(t),y2(t),…,yn(t))T,即

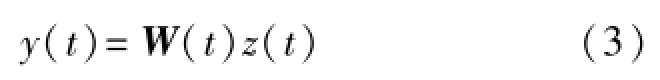
由于盲源分离问题存在顺序和幅度的不确定性,当全局矩阵G=W(t)Q(t)A(t)可表示成置换矩阵和对角阵的乘积时,即可认为y(t)是源信号s(t)的有效估计。

1.2 时变混合系统

在时变混合盲源分离中,常常用时变混合矩阵来描述混合系统的时变。文中考虑混合方式为时变线性瞬时混合的情形,并把时变混合矩阵A(t)建模成渐变模型。

为了表示方便,在时变混合系统中建立直角坐标系,如图2所示。源S1和S2(S2与坐标轴原点O重合)以及一个传感器X1固定,而另一个传感器X2以一定的速度v在x轴上的B、C两点之间来回运动,S1X1与x轴平行。若只考虑自由空间损耗,则可认为传感器接收到的信号的衰减因子为其与源之间的距离平方的倒数[5],因此图2所示的时变混合矩阵可表示为

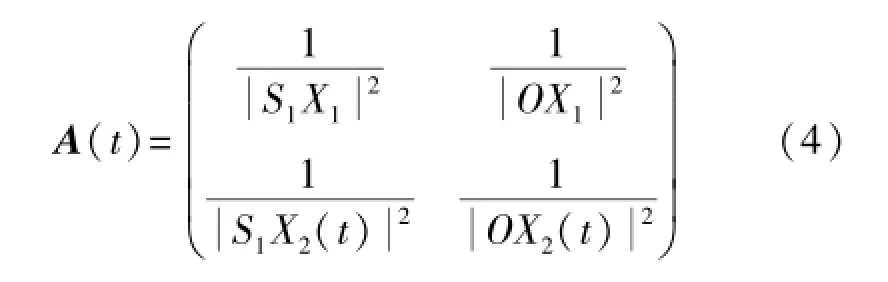
随着传感器X2的不断运动,混合矩阵不断变化,于是得到一个渐变的混合系统。由于源和传感器之间发生了相对运动,必然产生多普勒频移,即传感器接收到的信号是经过多普勒频移的混合信号,经算法分离后得到的信号也是带多普勒频移的信号。一般而言,通信系统接收端有消除多普勒频移的处理,但这并不是盲源分离算法解决的问题,所以,文中不予讨论。

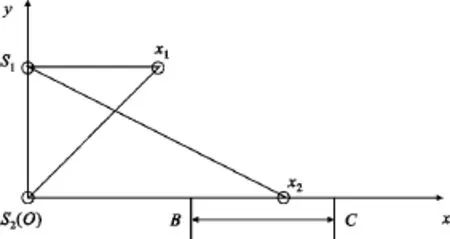
图2 时变混合系统模型Fig.2 Time-varying mixing system model

2 FastICA算法

FastICA算法由芬兰赫尔辛基工业大学学者提出,是盲源分离算法中一种快速有效的典型批处理算法,这种算法因无需设置迭代步长,迭代形式简单,且收敛速度快而被广泛运用。

FastICA算法往往以峭度作为非高斯性的度量,可定义以下代价函数[3]:

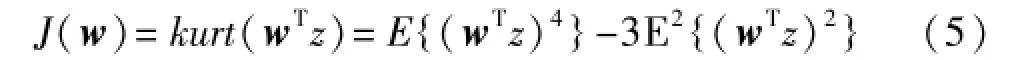
其中w是W的列向量。对上式求导,可得代价函数对w的梯度:

考虑到数据经过白化后有:E{(wTz)2}=‖w‖2=1,因此,可以得到FastICA算法的迭代公式:

在实际中,我们用所有样点的统计平均值来估计式(7)中的峭度和数学期望[6],然而,在时变混合盲源分离中,由于系统时变,要求以在线的方式对混合数据进行实时处理,因此FastICA算法不能直接用于解决时变混合盲源分离问题。为此,我们改进了FastICA算法。

3 改进的FastICA算法

在时变混合系统中必须采用在线算法进行实时处理,而要想使用式(5)有效地估计峭度,又要求利用更多的数据通过批处理的方式进行估计,为了解决这个矛盾,考虑如图2所示的时变混合信道,当传感器以低于50 km/h的速度运动时,在一段较短的时间间隔内混合矩阵变化很小,可以认为混合信道是基本时不变的,这时可以利用传统的FastICA算法进行分离,并且段与段之间实现在线处理。

首先将L个采样点等分成若干段,定义一个新的代价函数:

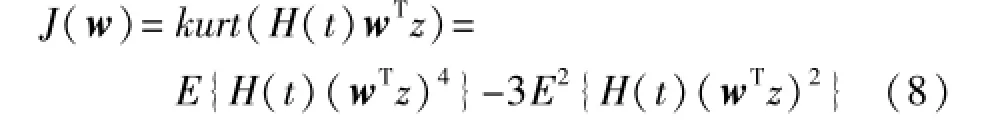
其中,H(t)是一个宽度为τ的窗函数,设当前处理第k段数据,则窗函数可表示为:

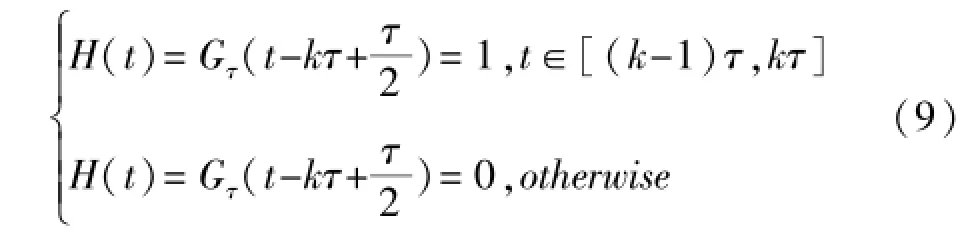
由式(8)可知,新的代价函数可以通过分段的方式进行近似在线估计,对w求导,可得到新的代价函数的梯度:

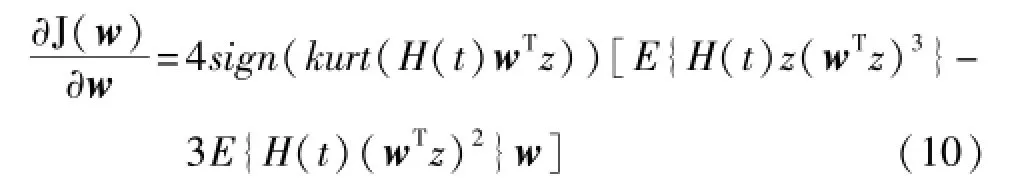
若τ的取值合适,不仅可以比较准确地估计出峭度,还能做以下近似替换,方便计算:

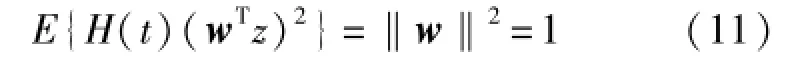
令新的代价函数的梯度与w相等,就得到一种新的不动点算法:

每次迭代后均对w做归一化处理,即使其范数为1:

在实际应用中,时间间隔长度应兼顾间隔时间内混合信道的时不变性,时间间隔越大,对峭度的估计就越准确,算法的精度就越高,但同时间隔时间内混合信道的时不变性越差;反之,间隔时间混合信道的时不变性越好,但对峭度的估计越不精确,算法的精度也越差。

我们把这种新算法称为改进的FastICA算法,为了方便表示,记为M-FastICA算法。由以上分析可知,当τ=L时,M-FastICA算法与FastICA算法相同;当τ=1时,M-FastICA算法变成普通的在线算法,但此时无法估计峭度;若τ的取值合适,则既可以较为准确地估计出峭度,又可以以近似在线的方式处理数据,这样就能跟踪混合系统的时变。

4 仿 真

下面通过Matlab仿真验证文中所提算法在时变混合系统中的分离性能。为了便于描述算法的分离性能,采用性能指数(PI)[7]和相似度[1]作为评价准则,其定义如下:

式中,gij表示全局矩阵G的第i行第j列元素。PI的值越接近于零,说明算法对混合信号的分离效果越好。

相似系数ξij(t)是衡量t时刻已经分离得到的输出信号波形与源信号波形之间相似程度的评价指标,其定义如下[10]:

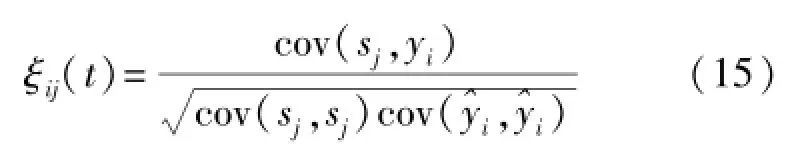
其中sj为源信号向量S的第j个源信号,yi为盲分离算法分离出的第i个信号,cov(sj,yi)=E{[sj-E[sj]][yi-E[yi]]}为sj和yi之间的协方差。

文中采用相似度系数以10为底的对数:ξ=lg[ξij(t)]来描述分离信号和源信号的相似程度,则该值越接近于0,则可以认为分离效果越理想。

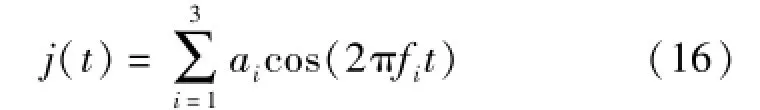
窗函数H(t)的宽度为τ=1 000个采样间隔,初始分离矩阵设为W(0)=I。

由于M-FastICA算法采用分段批处理的思想进行设计,每段数据采用相同的分离矩阵分离,对于每段数据,本文选用一个PI值来表示该段的分离效果。图3给出了NPCA算法和M-FastICA算法分段性能指数PI随采样点的变化关系曲线。由图3可知,M-FastICA算法收敛速度快于NPCA算法,采用M-FastICA算法得到的第一段数据(即前1 000个样点)的PI值较大,说明其分离效果较差,这主要是因为样点数少,算法尚未达到收敛;从第二段数据始, PI值较小,说明分离效果较好。

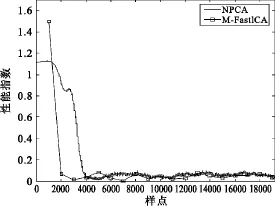
图3 NPCA算法和M-FastICA算法的相似度曲线Fig.3 PI curve of NPCA and M-FastICA algorithm

图4给出了各段源BPSK信号与分离得到的BPSK信号的相似度曲线,由图4可得到与图3相似的结论,第一段分离信号与源信号的相似度远低于其余各段的相似度,自第二段数据始,分离信号与源信号的相似度达到0.99以上,分离效果较好。

图4 NPCA算法和M-FastICA算法得到的各段数据的相似度曲线Fig.4 Similarity curves of each subsection of NPCA and M-FastICA algorithm

为进一步验证M-FastICA算法的性能,文中还仿真了该算法的误码性能。仿真中干信比取JSR= 10 dB,其他仿真条件和仿真环境与前面相同,图5给出了将混合信号直接解调得到的误码率和采用文中所提算法得到的误码率随信噪比SNR变化曲线。

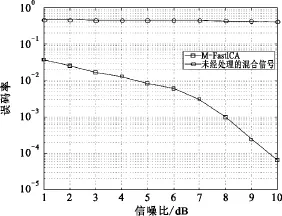
图5 误码率随信噪比变化曲线Fig.5 Curve ofthe BER versus SNR

由图5可知,在时变环境中,M-FastICA算法的误码性能随信噪比增大而提高,当信噪比满足SNR≥7 dB时,误码率随信噪比增大而快速减小,而当1 dB＜SNR＜7 dB时,误码率随信噪比增大而缓慢减小,主要原因是M-FastICA算法采用分段方式估计峭度,估计精度不够高,加之混合信道是时变的,所以,当信噪较低时,误码性能主要受算法分离精度的影响,随着信噪比的增加,算法的误码性能改善得不是很明显。

5 结 语

FastICA算法具有收敛速度快和迭代简单的优点,但其属于批处理算法,不能实时跟踪信道变化。为了提高算法收敛速度和跟踪时变信道的性能,文中在FastICA算法的基础上,运用分段的思想将混合信号分成若干段,由于混合信道缓慢变化,因而可近似认为在各段数据中混合信道是时不变的,因此,可在各段数据中采用FastICA算法进行分离,这样我们就得到一种改进算法——M-FastICA算法,该算法保持了传统FastICA算法简洁的迭代。仿真实验表明,在时变环境中,M-FastICA算法收敛速度快于NPCA算法,并且能有效地抗多音干扰。

[1] 张发启,张斌,张喜斌.盲信号处理及应用[M].西安:西安电子科技大学出版社,2006.

Zhang Faqi,Zhang Bin,Zhang Xibin.Operation and Application of Blind Signal[M].Xi'an:Xidian university publisher,2006.

[2] BELOUCHRANI A,KARIM A M,CARDOSO J F.A Blind Source Separation Technique Using Second-order Statistics[J].IEEE Trans.On Signal Processing, 1997,45(02):434-444.

[3] HYVARINEN A.Fast and Robust Fixed-point Algorithms for Independent Component Analysis[J].IEEE Transactions on Neural Networks,1999,10(03):626-634.

[4] VICENTE Z,PIERRE C.Robust Independent Component A-nalysis by Iterative Maximization of the Kurtosis Contrast with Algebraic Optimal Step Size[J].IEEE Transactions on Neural Networks,2010,21(02):248-261.

[5] PUSKAL P,UMUT O,DENIZ E,et al.Recursive Complex BSS via Generalized Eigendecomposition and Application in Image Rejection for BPSK[J].Signal Processing,2007,88(2008):1368-1381.

[6] 毛欣,徐慨,刘杰.盲信号分离技术现状与发展动态[J].通信技术,2013,46(08):24-26.

MAO Xin,XU Kai,LIU Jie.Present Situation and Development of Blind Signal SeparationTechnology[J].Communications Technology,2013,46(08):24-26.

[7] AMARI S,CHEN T P,CICHOCKI A.Stability Analysis of Learning Algorithms for Blind Source Separation[J]. Neural Network,1997,10(08):1345-1351.

CHEN Hai-ping(1989-),male,graduate student,majoring in blind signal processing.

张 杭(1962—),女,硕士,教授,博士生导师,主要研究方向为盲信号处理,通信抗干扰等;

ZHANG Hang(1962-),female,M.Sci.,professor,doctoral tutor,mainly specialized in blind signal processing,communication anti-jamming,etc.

路 威(1978—),男,博士,副教授,主要研究方向为通信信号处理、通信抗干扰等;

LU Wei(1978-),male,Ph.D.,associate professor,maily engaged in communication signal processing,communication anti-jamming,etc.

张 江(1984—),男,博士,工程师,主要研究方向为盲信号处理等。

ZHANG Jiang(1984-),male,Ph.D.,engineer,principally working at blind signal processing,etc.

On-Line FastICA Algorithm for Time-Varying Mixing System

CHEN Hai-ping1,ZHANG Hang1,LU Wei1,ZHANG Jiang2
(1.Institute of Communication Engineering,PLA University of Science and Technology,Nanjing Jiangsu 210007,China; 2.No.63 Research Institute,PLA General Staff Headquarters,Nanjing Jiangsu 210007,China)

Most existing BSS(Blind Source Separation)algorithms are developed by assuming that the mixing matrix is invariable.However,the mixing matrix is commonly time-varying in practical communication system.The traditional fast fixed-point(FastICA)algorithm cannot directly separate the sources mixed in time-varying system,although is very fast in convergence.Thus in order to accelerate the convergence rate and improve the tracking performance for time-varying system,the FastICA algorithm is modified by dividing samples into several subsections,thus to estimate the kurtosis and separate the sources off-line in each subsection.Simulation results indicate that the modified FastICA algorithm could track the time-varying system effectively.

blind source separation;time-varying;FastICA;convergence rate;on-line algorithm

TN911.7

A

1002-0802(2014)02-0136-05

10.3969/j.issn.1002-0802.2014.02.003

陈海平(1989—),男,硕士研究生,主要研究方向为盲信号处理;

国家自然科学基金:欠定条件下基于扰信分离的信干比增强方法研究(No.61001106)

Foundation Item:National Natural Science Foundation of China:Signal-to-Jamming Ratio Enhancement Research based on the Separation of Interference and Signal in the Underdetermined Condition(No.61001106)