基于PAM分解面向判决的Multi-h CPM载波相位同步*

谢 滔,钟 声,王世练,张 炜

(1.国防科学技术大学电子科学与工程学院,湖南长沙410073; 2.中国工程物理研究院电子工程研究所,四川绵阳621900)

基于PAM分解面向判决的Multi-h CPM载波相位同步*

谢 滔1,钟 声2,王世练1,张 炜1

(1.国防科学技术大学电子科学与工程学院,湖南长沙410073; 2.中国工程物理研究院电子工程研究所,四川绵阳621900)

多指数连续相位调制(Multi-h CPM,Multi-h Continuous Phase Modulation)具有频谱效率高,抗误码性能好的特点,具有广泛的应用前景,但同步问题一直是Multi-h CPM接收机的难点之一。在已有单指数CPM载波相位同步算法的基础上,研究了一种基于PAM分解面向判决的Multi-h CPM信号载波相位同步算法,为了有效界定所提出算法的性能,推导出了Multi-h CPM载波相位估计的修正克劳美罗限(MCRB)。仿真结果表明,在较大多普勒频率及其变化率的环境下,该载波相位算法的估计性能良好且能逼近其MCRB。

Multi-h CPM 载波相位同步 PAM分解 面向判决

0 引 言

在众多的调制方式中,连续相位调制信号(CPM信号)具有恒包络特性,它用于承载信息的相位轨迹连续变化,因此该类信号拥有较高的带宽效率[1]。多指数连续相位调制具有若干个随着时间循环变化的调制指数,通过选择合适的调制指数,一方面,可以使相位网格图上的相邻相位路径难以快速合并,从而增加各路径对应的译码序列间的最小欧氏距离,提高抗误码性能;另一方面,可以使频谱更加紧凑,带外滚降速度更快,提高带宽利用率[2]。因此多调制指数连续相位调制体制不仅具有一般CPM调制的优点,而且抗误码性能更好,频谱效率更高,在未来的遥测领域中具有巨大的潜在优势。但是Multi-h CPM解调复杂度高、同步困难,一直限制着Multi-h CPM应用与发展。

同步一直是Multi-h CPM接收机的关键技术和难点之一。由于Multi-h CPM信号是非线性调制且具有记忆特性,当前信号状态不但与当前的码元有关,更和过去的码元有关,加入多个循环周期变化的调制指数之后又增加了载波同步的难度与复杂度。目前,在Multi-h CPM信号应用最多的UHF军事卫星通信系统中,均采用数据辅助的同步方法。在UHF卫星通信的美军标MIL-STD-188-181B中,同步的前导码元序列中有一组是用于Multi-h CPM信号的载波同步。虽然利用前导码元可以较好地完成Multi-h CPM系统的同步,但是前导码元的引入也造成了额外信号带宽的使用对原本就是以解调复杂度换取功率效率和频谱效率的Multi-h CPM系统而言,利用导频信号或前导码元进行同步显得得不偿失。

到目前为止,针对单指数CPM的载波相位同步算法为数不多,主要分为两类:第一类为仅针对全响应CPM信号的p次幂载波相位同步算法[3],而p次幂法会使得接收信号的信噪比急剧恶化;第二类为面向判决(DD,Decision-Directed)的载波相位同步算法及其变种,即通过对接收信号进行线性分解以降低其实现复杂度,例如基于Wash分解的DD载波相位同步算法[4]、基于PAM分解的DD载波相位同步算法[5]。本小节在文献[5]的基础上,对仅针对于单指数CPM的基于PAM分解面向判决的载波相位同步算法进行改进,给出一种适用于Multi-h CPM的基于PAM分解面向判决的载波相位同步算法(为了便于表述,简称为DD-PS算法)。

文中在给定载波相位估计系统模型的前提下,推导了Multi-h CPM信号的载波相位估计性能的修正Cramer-Rao限。对仅针对于单指数CPM的基于PAM分解的DD载波相位同步算法进行改进,给出了一种适用于Multi-h CPM的基于PAM分解的DD载波相位同步算法。仿真表明,在较大多普勒频率及其变化率的环境下,该载波相位算法的估计性能良好且能逼近其MCRB限。

1 Multi-h CPM的信号表示

1.1 Multi-h CPM的一般表达式

Multi-h CPM信号的一般表达式可以定义为

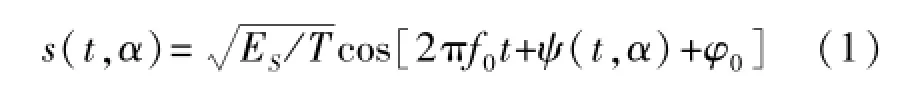
其复基带解析式可以表示为

式中,Es为信号码元能量,T为码元间隔宽度,φ0表示初始相位,α=(α0,α1,…)为发送的M进制信息符号序列,即αn∈{±1,±3,…,±(M-1)}。=/p(其中和p是互素整数)为调制指数,其取自一个有限的离散调制指数集合∏={h0,h1,…, hNh-1},且在每个符号码元周期内保持不变,若干调制指数∈∏是以Nh周期循环变化,表示n模Nh的运算。对于Multi-h CPM信号而言,Nh＞1。相位响应脉冲为,频率响应脉冲f(t)在时间间隔(0,LTs)内受限,即q(LTs)=1/2,L为部分响应长度。f(t)最为常见的脉冲形状分别为矩形成型脉冲(LREC),升余弦成型脉冲(LRC)以及高斯成型脉冲(GMSK)。文中后面的仿真选用M=4、∏={4/16,5/16,}、L=3、LRC成型的ARTM Tier 2信号。

1.2 Multi-h CPM基于PAM分解的表达式

已经证明,单指数CPM信号可以通过一组有限数量的幅度调制冲的线性组来实现其精确表达,即PAM(Pulse Amplitude Modulation)分解算法[6-7], 2005年Perrins将其推广到Multi-h CPM信号的PAM分解中[8]。

Multi-h CPM信号的PAM分解可以表示为

式中,N=Qp(2p-1)表示PAM脉冲波形的数量,P= lbM且Q=2L-1。由文献[8]可知,伪符号ak,n与PAM脉冲波形gk,n(t)分别由信号符号{am}以及Multi-h CPM的相位响应通过一系列非线性变换得到。图1分别给出了ARTM Tier2信号奇偶时刻分解后的PAM脉冲波形。

图1 ARTM Tier2信号的PAM脉冲波形Fig.1 Pulse waveforms of ARTM Tier2

2 基于PAM分解面向判决的载波相位同步算法

在绝大多数情况下,本地恢复的载波频率不可能与真实的载波频率完全相同,因此,除由固定载波初相和传播延迟引起的载波相位偏移外,载波频率同步模块产生的残留载波频偏会导致接收信号的相位出现缓慢的漂移,从而造成收发两端载波相位不同步。在非相干解调系统中,由于其本身所具备的抗残留载波频偏和载波初相的特性,因此载波相位的同步可以不用考虑。但是在相干解调系统中,载波相位对接收系统的性能影响却很大,因此必须估计载波相位并进行相应的相位补偿以此实现载波相位的同步。

2.1 系统模型

在AWGN信道条件下,接收的Multi-h CPM信号的复基带表达式(2)可改写成:

式中,τ为传播延迟即符号定时误差,ζ为调制指数同步误差。假设接收信号已经完成了载波频偏的估计与校正,则载波相位为θ=θ0+2πΔfτ+2πΔft且Δf表示经载波频率同步模块校正后的残留载波频偏。虽然由于残留载波频偏Δf的影响使载波相位成为了随时间变化的参数量,但是为利用ML准则,在本节的相关算法推导中仍然将θ处理成一个确定但是未知的参数。

2.2 Multi-h CPM载波相位估计的修正Cramer-Rao限

为了有效界定载波相位恢复算法的性能,这里先推导出Multi-h CPM载波相位估计的MCRB。在AWGN信道下,Multi-h CPM信号关于载波相位θ估计的MCRB可定义为

式中,s(t,θ,Iθ)表示式(5)中的复基带信号部分,Iθ={α,f,τ,ζ}则表示需要通过求数学期望去掉的未知参数矢量。对式(6)分母项求Iθ的数学期望,可得

式中,归一化等效噪声带宽BθTs=1/(2L0),将式(7)代入式(6),则Multi-h CPM信号的关于载波相位θ的MCRB限可表示为

从式(8)可以看出,Multi-h CPM信号载波相位的MCRB(θ)限与Multi-h CPM信号的具体调制参数无关,而只与归一化等效噪声带宽和符号信噪比有关。

2.3 基于PAM分解面向判决的载波相位同步

假设系统已完成了调制指数的同步和符号定时同步,所以假设式(5)中的调制指数同步误差ζ和定时同步误差τ已经被理想的同步模块校正了,即ζ=0和τ=0。此时的信号模型可以简化为

根据ML准则,式(9)的未知参数θ的似然函数可以表示为

将s(t,α)的基于PAM分解的表达式(4)代入式(10),得到

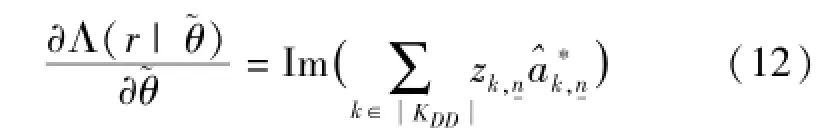
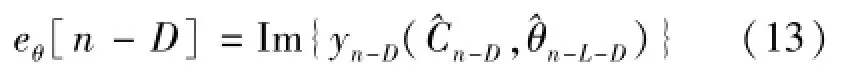
图2 DD-PS算法的原理框Fig.2 Schematic diagram of DD-PS algorithm

根据式(13),以ARTM Tier2信号为例阐述DD-PS算法的特性。图3给出了当=2×12时,ARTM Tier2信号的DD-PED的鉴相S曲线,其中δθ=θ-表示载波相位偏差。从图中可以看出, DD-PED的有效估计区间分别为[-π/32,π/32]。对载波相位估计而言,由于DD-PED的鉴相S曲线一共具有2p-1个相位模糊点,因此载波相位同步的锁相环会在任意一个相位模糊点入锁,而在噪声的影响下,载波相位估计值的抖动会使得锁相环输出可能会向另外一个模糊点出现周期滑动[9]并且锁定,造成估计值与真实值θ之间存在一个随机且时变的相位差,从而引起系统的BER性能损失,因此对于Multi-h CPM的载波相位同步中,环路滤波器的归一化等效环路噪声带宽应尽可能地窄,以提高带内信噪比从而降低周期滑动的次数[9]。

图3 DD-PS算法的鉴相S曲线(ARTM Tier2,=2×12)Fig.3 S curve of DD-PS algorithm (ARTM Tier2,=2×12)

3 仿真分析

下面来验证所改进的DD-PS算法正确性及性能,仍然在ARTM Tier2系统上进行性能仿真,仿真参数如下:①符号速率为Rs=5 Ms/s;②多普勒频率为200 kHz,多普勒频率的一阶变化率为20 kHz/s,多普勒频率的一阶变化率为3 kHz/s,载波初相为0.1π;③环路滤波器为三阶数字锁相环,归一化等效环路噪声带宽为BθT=1×10-2;④信道为加性AWGN信道;⑤采用128状态的基于PAM分解的低复杂度序列检测进行符号判决;⑥估计结果用相位误差方差(VAR,Phase Error Variance)来衡量其性能,即:

式中,[n]表示第n次蒙特卡洛仿真的θ估计结果。图4给出了ARTM Tier2信号的DD-PS算法的载波相位估计的VAR性能。从图4中可以看出,随着信噪比和的增加,DD-PS算法的载波相位估计的VAR性能有很好的改善。与=2×3时相比,

=2×12时估计性能在中低信噪比条件下更接近于其MCRB,但是的增加在带来的性能一定程度改善的同时也意味着系统复杂度的提高,因此在实际中的取值需要根据具体的应用做出合理的选择。

图4 Multi-h CPM信号的DD-PS算法估计的VAR性能(ARTM Tier2)Fig.4 Estimation performance of DD-PS algorithm(ARTM Tier2)

4 结 语

文中推导了Multi-h CPM载波相位估计的MCRB。然后在单指数载波相位同步算法的基础上进行改进,给出了一种适用于Multi-h CPM的载波相位同步的DD-PS算法。仿真结果表明,通过适当合理选择等参数,在较大的多普勒频率及其变化率的条件下,DD-PS算法VAR性能良好,在中低信噪比条件下能逼近其MCRB。

[1] 李燕斌,骆小谚,李寅博.部分响应CPM信号解调器的FPGA设计[J].通信技术,2011,44(02):13-15.

LI Yan-bin,LUO Xiao-yan,LI Yin-bo.Design of Partial Responses CPM Demodulator based on FPGA[J]. Communications Technology,2011,44(02):13-15.

[2] 朱宏权,吴岭,游莎莎,等.Multi-h CPM体制误码和频谱性能研究[J].飞行器测控学报,2010,29(05):56-59.

ZHU Hong-quan,WU Ling,YOU Sha-sha,et al.Study on BER and Spectrum Performance of Multi-h CPM System[J].Journal of Spacecraft TT&C Technology,2010, 29(05):56-59.

[3] MAZUR B A,Taylor D P.Demodulation and Carrier Synchronization of Multi-h Phase Codes[J].IEEE Transactions on Communication,1981,29(03):1041-1045.

[4] TANG Weiyi.A Receiver for Continuous Phase Modulation in Walsh Signal Space[D].Manitoba,Canada:University of Manitoba,1998.

[5] SAYAK B.Reduced-complexity Joint Frequency,Timing and Phase Recovery for PAM based CPM Receivers[D]. US,Kansas:University of Kansas,2009.

[6] LAURENT P.A.Exact and Approximate Construction of Digital Phase Modulation by Superposition of Amplitude Modulated Pulses(AMP)[J].IEEE Transactions on Communications,1986,34(02):150-160.

[7] MENGALI U,MORELLI M.Decomposition of M-ary CPM Signals into PAM Waveforms[J].IEEE Transactions on Information Theory,1995,41(05):1265-1275.

[8] PERRINS E,RICE M.PAM Decomposition of M-ary Multi-h CPM[J].IEEE Transactions on Communications,2005,53(12):2065-2075.

[9] COLAVOPLE G,RAHELI R.Reduced-complexity Detection and Phase Synchronization of CPM Signals[J]. IEEE Transactions on Communications,1999,45(09): 1070-1079.

XIE Tao(1989-),male,M.Sic.,majoring in wireless communication technology.

钟 声(1981—),男,博士,主要研究方向为遥测遥控技术;

ZHONG Sheng(1981-),male,Ph.D.,majoring in telemetry,tracking and command technology.

王世练(1976—),男,副教授,主要研究方向为无线通信对抗;

WANG Shi-lian(1976-),male,associate professor,mainly working at wireless communication countermeasures.

张 炜(1972—),女,副教授,主要研究方向为无线通信技术。

ZHANG Wei(1972-),female,associate professor,mainly working at wireless communication technology.

A Decision-Directed Carrier Phase Recovery Algorithm based on PAM Decomposition for Multi-h CPM

XIE Tao1,ZHONG Sheng2,WANG Shi-lian1,ZHANG Wei1
(1.School of Electronic Science and Engineering,National Univ.of Defense Technology,Changsha Hunan 410073,China; 2.Institute of Electronic Engineering,China Academy of Engineering Physics,Mianyang Sichuan 621900,China)

Multi-h Continuous Phase Modulation with features of high spectral efficiency and good performance of error resilience has broad application prospects.However,the synchronization issue has been one of the difficulties for Multi-h CPM receiver.Based on a existing single-h CPM carrier phase recovery algorithm,a decision-directed carrier phase recovery algorithm based on PAM decomposition for Multi-h CPM is studied in this paper.In order to define the performance of the proposed algorithm effectively,the MCRB of multi-h CPM carrier phase estimation is deduced.The simulation results show that,in the environment of large doppler frequency and gradient of doppler frequency,the estimation performance of the algorithm is good and it can approach the MCRB.

multi-h CPM;carrier phase recovery;PAM decomposition;decision-directed

TN919.6

A

1002-0802(2014)06-0595-05

10.3969/j.issn.1002-0802.2014.06.002

谢 滔(1989—),男,硕士,主要研究方向为无线通信技术;

2014-04-04;

2014-05-14 Received date：2014-04-04;Revised date：2014-05-14