彩色多聚焦图像邻域融合算法的改进*

刘艳英,凌朝东

(1.华侨大学信息科学与工程学院,福建厦门361021;2.厦门市专用集成电路系统重点实验室,福建厦门361008)

彩色多聚焦图像邻域融合算法的改进*

刘艳英1,2,凌朝东1,2

(1.华侨大学信息科学与工程学院,福建厦门361021;2.厦门市专用集成电路系统重点实验室,福建厦门361008)

针对彩色多聚焦图像融合存在色彩分布不均、斑效应问题,提出一种图像空间信息和颜色信息分离研究的改进算法。首先对源图像进行HSV变换并分离各分量,然后表示空间信息的V分量进行小波分解,最高分解层高频系数选用基于邻域的对比度取大融合规则,而其余分解系数选取基于邻域梯度的加权融合规则。其次重构得到融合图像V分量,表示颜色信息的H、S分量采用源图像与融合图像间V分量欧氏距离取小规则,最后进行HSV逆变换得到融合图像。经MATLAB仿真,该算法可有效缓解融合图像色彩分布不均及斑效应现象。

图像融合 彩色空间变换 对比度 梯度加权

0 引 言

图像融合是数据融合的重要组成,根据处理层不同将其划分为像素级、特征级和决策级[1]。像素级融合为基础级的数据融合,是另外两种融合的基础,得到广泛研究和应用。像素级融合根据数据处理域的不同分为空间域和变换域,空间域融合过程简单,易于实现实时处理;变换域融合过程复杂,但是图像质量得到很大提高,随着人们对图像视频质量要求的日益提升,变换域融合得到相当广泛地研究。影响图像融合质量的另一关键因素是融合规则,有基于像素、窗口和邻域3种。由于图像相邻像素之间存在很强的相关性,而基于像素的融合忽略像素间的相关性很难取得令人满意的融合效果;基于窗口的融合规则虽然考虑了相邻像素的相关性但忽略了窗口边缘的像素点;基于邻域的融合规则全面考虑像素相关性,有效抑制了拼接痕迹并降低了噪声敏感度,提高了图像信息选取正确率[2]。在实验过程中发现基于邻域特征的融合规则应用于彩色多聚焦图像融合时存在斑点,色彩分布不均问题;而加权融合无论是基于窗口还是邻域,融合得到的图像对比度虽然降低但色彩分布均匀。鉴于此启发,对彩色多聚焦图像基于邻域的融合算法进行改进。

1 彩色模型和Mallat算法

1.1 RGB和HSV变换

视觉对彩色图像的敏感度远远高于灰度图像:彩色分辨率可达上千种,而仅能识别十几个灰度级,彩色图像处理得到广大学者的关注和研究[3]。彩色图像与灰度图像间的本质区别为:彩色图像像素点用矢量(通常包括3个分量,如R、G、B)表示,而灰度图像像素点仅仅用一个标量来反映。彩色图像的处理手段有单色和矢量值技术,单色技术忽略色彩分量间的联系将灰度图像的处理技术分别作用于各色彩分量;矢量值技术运算比较复杂,且目前对图像从标量过渡到矢量的认识还存在不足,多数情况下仍采用单色技术处理彩色图像。于是选择合适的色彩空间,降低色彩分量间的相关性成为彩色图像处理的重要前提。HSV色彩空间可以较好地分离图像的空间和颜色信息,在基于单色技术的融合中可取得比RGB空间更好的视觉效果[4]。

HSV彩色空间由CIE(国际照明委员会)色彩空间演变而来,是目前最符合人类视觉感知的模型。H、S、V依次表示图像的色调(Hue)、饱和度(Saturation)、亮度(Value)。色调即颜色属性,用角度来衡量,取值范围是0°到360°;饱和度代表颜色的纯净程度,常将其与色调合称为色度;亮度则表示图像明亮程度,是对灰度的衡量;饱和度与亮度的取值范围都是0到1。从RGB到HSV空间的变换表达式为:v′=0时s=0,h无意义。式中v′=max(r,g,b),u′=min(r,g,b),h′取值分情况表示如下。

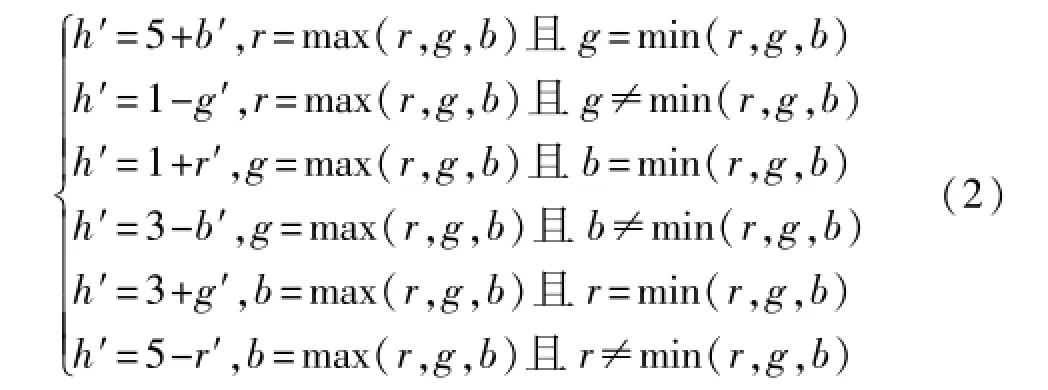
式中,r′=(v′-r)/(v′-u′),g′=(v′-g)/(v′-u′),b′= (v′-b)/(v′-u′)。设i=、f=h/60-i分别表示h′的整数和小数部分,i=6时与i=0相同;v= 255v′、u=255v(1-s)、m0=255v[1-s(1-f)]、m1= 255v(1-sf),则HSV逆变换过程如下:

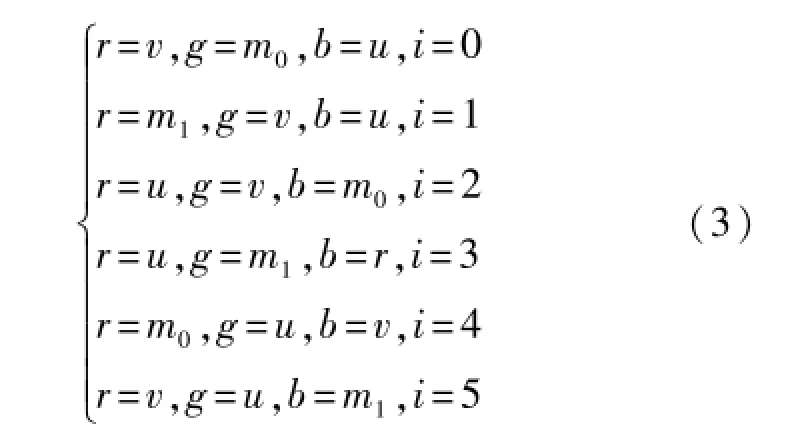
1.2 小波Mallat算法

小波变换是多尺度变换工具之一,时域频域的不同位置分辨率不同:在频域内,低频分量频率分辨率比较高,高频分量频率分辨率相应较低;而在时域内,低频分量时间分辨率却较低,高频分量时间分辨率较高,即低频系数可以反映图像的轮廓信息,而高频系数可以表现图像的细节信息。

用“*”表示矩阵的共轭,则二维小波Mallat分解算法的重构表达式为:

2 图像质量评价

通常选择主观与客观相结合的方式评估融合图像的质量[5]。主观评价一般对图像的全局效果进行评定,如有无重影、整体亮度、色彩反差和整体色彩分布等。该方法简单快捷,容易因个体差异出现评价不一致的情况,但是只有图像客观评价满足要求后才有进一步的客观评价。客观评价是对图像质量进行定量分析,被作为算法性能比较的量化指标。

灰度图像融合常用的客观评价标准有平均梯度、方差和交叉熵,而本次试验对象为彩色图像,额外定义了平均饱和度来反映图像的颜色纯净程度。为方便评价标准的表述,进行以下参数定义:M、N依次表示图像行、列像素数,V(x,y)、S(x,y)依次表示图像在点(x,y)处的亮度、饱和度,L表示图像灰度级数,pA(i)、pB(i)、pF(i)表示第i灰度级的概率,亮度分量与灰度图像中的灰度相对应,在计算时将其归化至0～255。

平均梯度可以表示图像的清晰度并反映其细节部分的反差和纹理变换特征,平均梯度越大图像清晰度越大,计算公式如下:

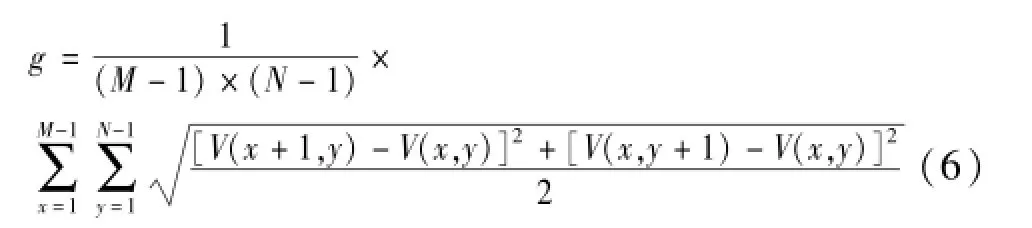
方差表示变量的离散程度,反映图像对比度:值越大说明对比度越大,颜色显示越鲜艳醒目,运算过程如下:

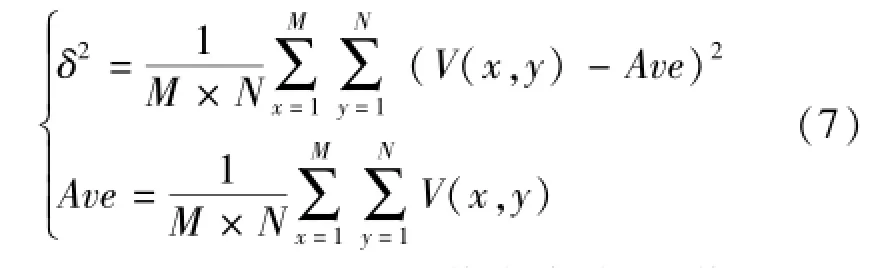
平均梯度和方差反映图像自身特征,值越大图像显示效果越好。而平均交叉熵能够反映融合图像从源图像中获得的信息量:平均交叉熵越小,融合图像从源图像中获得的信息量越大,图像质量越高。计算过程如下:

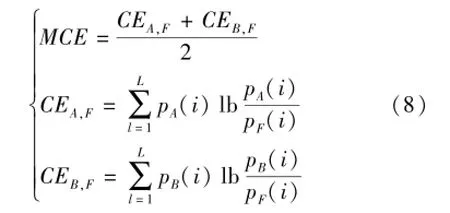
式中,CEA,F、CEB,F分别表示源图像A、B和融合图像的交叉熵。另外以整幅图像的平均饱和度来衡量图像的颜色纯净程度,平均饱和度定义如下:

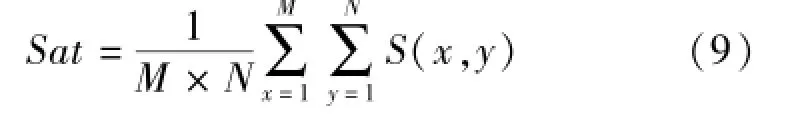
3 图像融合实现

3.1 低频融合规则

虽然多聚焦图像清晰和模糊区域的区别主要体现在细节部分,即集中在高频系数,但是低频系数对图像的整体轮廓具有决定性作用,仍需要合理地融合规则来改善融合图像的视觉质量。常用的加权平均法能有效消除噪声,并且在基于窗口和邻域的融合过程中不会产生“块效应”和“斑效应”,不足之处是图像对比度下降。另外还有绝对值取大,方差取大,平均梯度取大,邻域能量取大[6-7],但是这些融合规则注重图像低频变化而忽视其均匀程度,基于邻域融合时会出现斑点效应[8]。平均梯度越大,图像的边界点或影线附近的灰度差距越明显,显示越清晰。采用领域平均梯度取大的融合规则可以保留这些差异,得到轮廓清晰的图像。将该融合规则与加权平均相结合,既可以保留图像的轮廓信息,也可以改善加权平均融合图像对比度低的现象。

设邻域窗口大小为m×n,gA(x,y)、gB(x,y)表示图像A、B在以点(x,y)为中心的邻域内的平均梯度。CA(x,y)、CB(x,y)、CF(x,y)依次表示源图像A、B和融合图像F在点(x,y)处的低频系数,则融合计算表达式如下:

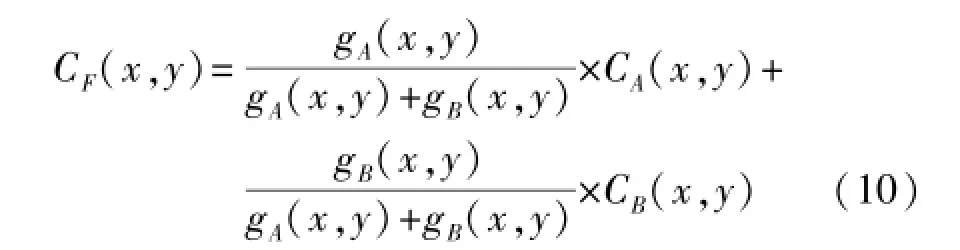
3.2 高频融合规则

人类视觉系统的响应取决于目标物体相对于背景的亮度变化率,而不是其绝对亮度值,即对比敏感度高,于是基于对比度的融合规则可以获得更符合人类视觉感知的融合图像。Weber对比度定义为:Cw=ΔL/L,ΔL为观测目标与背景亮度之差,L为背景亮度。根据Weber对比度以及小波变换系数的意义,定义图像j层小波分解的小波方向对比度为:

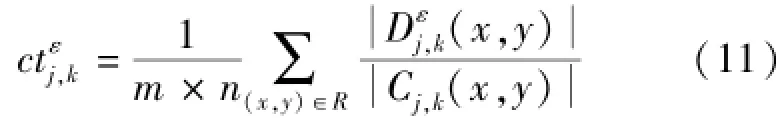
式中ε=1,2,3分别表示水平、垂直、对角线三个子方向,k=A,B表示源图像A和B,、分别表示以点(x,y)为中心的邻域R内的小波高频系数绝对值和、低频系数绝对值和。以Dε

j,F(x,y)表示j层融合后点(x,y)的小波高频系数,则基于区域对比度的高频系数融合规则算法表示如下:

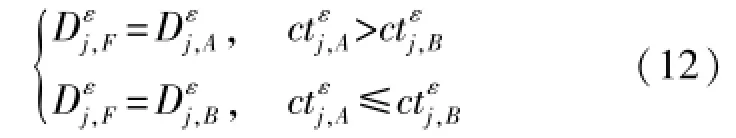
3.3 图像融合过程

Nunez J等人提出小波变换与彩色空间变换相结合可以同时保留图像的空间信息和颜色信息[9],下文以两幅图像融合为例,描述图像在HSV空间基于邻域融合的处理过程。

1)首先将严格配准的两幅源图像A和B进行HSV变换,得到它们的色调分量HA、HB,饱和度分量SA、SB以及亮度分量VA、VB。

2)对亮度分量VA、VB分别进行j层小波分解,得到它们的小波分解系数。然后计算最高分解层m×n邻域内高频系数的小波方向对比度,并计算其余系数m×n邻域内的平均梯度。

3)小波系数进行融合处理:采用式(12)计算融合图像最高分解层的高频系数,采用式(10)计算融合图像的其余分解系数。

4)将融合后的小波分解系数进行逆变换,重构获取融合图像的亮度分量VF。

5)融合处理后所得图像各像素点的亮度分量更接近源图像清晰部分的像素点,即融合图像与清晰部分的亮度差更小。欧氏距离是一种简单的表示差距的方式,计算融合图像与源图像亮度分量间的欧氏距离,欧氏距离越小说明对应像素点来自清晰部分的可能性越大,取此像素点的色调分量与饱和度分量作为融合图像的对应分量。融合图像色调HF、饱和度SF计算过程表示如下:

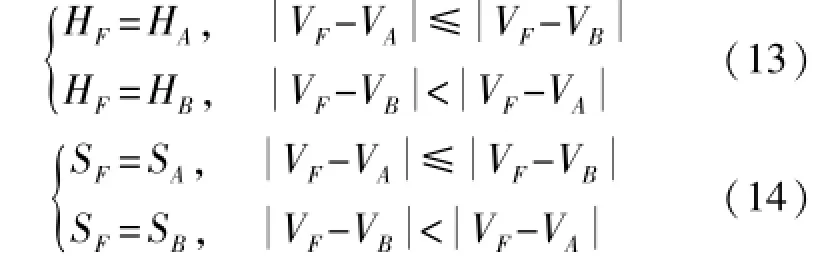
6)对融合图像进行HSV逆变换,得到RGB图像,至此完成彩色多聚焦图像融合。

4 融合结果分析

4.1 邻域大小及分解层数选择

虽然基于邻域的融合规则可以比单个像素点获得更多信息,但是目前仍没有可遵循的标准对邻域大小进行选取。邻域太小不能包含图像的有效信息,太大则会引入干扰信息并加大运算量。依次对3×3、5×5、7×7、9×9的邻域仿真,发现随着邻域的增大融合图像质量并没有提高而仿真速度却下降了,于是本次实验选择3×3的邻域。

基于3×3邻域,采用文中提出的融合算法依次进行2至5层分解融合仿真,观察2至4层分解融合图像差别不大,而5层分解融合图像质量明显下降。2至4层融合图像的客观评价指标如表1所示,三者饱和度相差不大,暂不考虑。比较另外三个指标发现2层和4层均优于3层,2层的平均梯度和方差优于4层,交叉熵却劣于4层。另外,分解层数越多计算量越大,所以选取2层分解为文中算法的最佳分解层数。

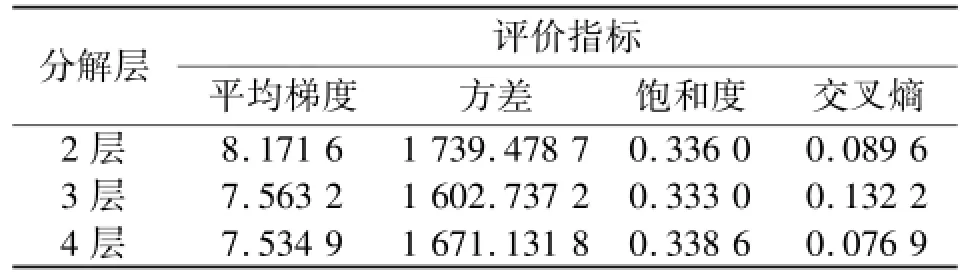
表1 3×3不同分解层评价指标比较Table 1 Evaluation index of different decomposition layeres in 3×3

4.2 融合图像比较

本次实验图像的配准与融合均是在MATLAB R2010b环境下进行。实验所用原始图像是由佳能550D单反相机对同一场景选取不同聚焦点拍摄而得,图像大小为768×512。文中对比了两组仿真,第一组采用文献[7]的算法,最高分解层的高频系数采用基于邻域对比度取大的融合规则,其余系数采用平均梯度取大的融合规则;第二组采用文中算法。两组仿真均采用双正交“bior2.2”小波基,进行2层分解,源图像和融合图像如图1、图2、图3和图4所示。

图1 左聚焦图像Fig.1 Left focus image

图2 右聚焦图像Fig.2 Right focus image

图3 文献[7]算法Fig.3 Algorithm of paper[7]

图4 文中算法Fig.4 Algorithm of this paper

观察以上各图,发现两种融合算法得到的融合图像质量均得到改善,图3与图4的左侧视觉效果相差不大,但是图3右侧却密密麻麻分布着大小不同的斑点,即图像整体色彩分布不均匀;图4没有斑点,整体色彩分布过渡平衡,视觉效果优于图3。现将两组仿真得到的融合图像和源图像的客观评价指标列于表2中。

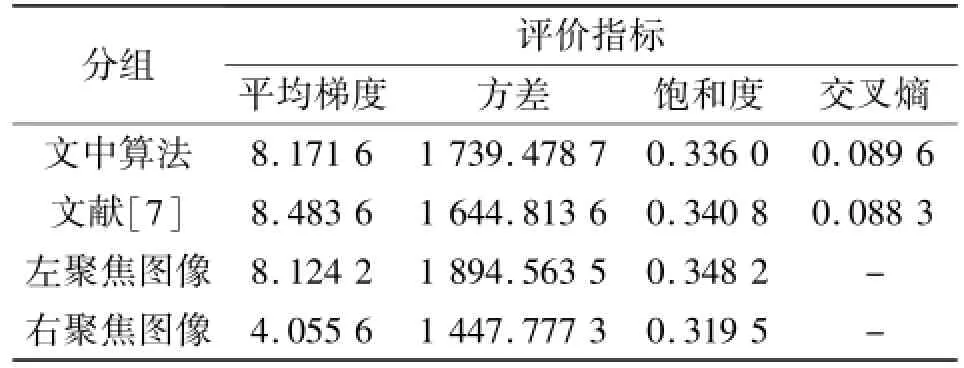
表2 两种算法评价指标Table 2 Evaluation index of two algorithms

比较以上客观评价指标,两种算法融合图像的平均梯度、饱和度和交叉熵差别不大,文中算法稍劣于文献[7],但文中算法的方差优于文献[7]的方差,即图像对比度得到一定提高。主客观评价相结合,在客观指标浮动不大的情况下,文中算法得到的融合图像没有斑效应、色彩分布均匀视觉效果良好,显然占据一定优势。

5 结 语

HSV空间可以有效分离图像的空间信息和颜色信息,基于邻域梯度加权的融合规则既考虑了图像的变化率,同时也考虑了其均匀性;而基于对比度的融合规则符合人类视觉对比敏感度高的特性。实验表明文中算法有效克服了基于区域的彩色多聚焦图像融合产生的斑效应,并提高了图像对比度,是一种有效的融合算法。

[1] 方辉,尹忠科.基于NSCT的区域能量图像融合算法[J].通信技术,2010,43(03):137-141.

FANG Hui,YIN Zhong-ke.An Image Fusion Algorithm based on Local Energy Using NSCT[J].Communication Technology,2010,43(03):137-141.

[2] PIELLA G.A General Framework for Multiresolution Image Fusion:from Pixels to Rgions[J].Information Fusion,2003,4(04):259-280.

[3] ZHAO H,LI Q,FENG H.Multi-focus Color Image Fusion in the HSI Space Using the Sum-modified-laplacian and A Coarse Edge Map[J].Image and Vision Computing,2008,26(09):1285-1295.

[4] 常化文,陈春香.基于HSV变换与小波变换的遥感图像融合[J].计算机工程与设计,2007,28(23):5682-5694.

CHANG Hua-wen,CHEN Chun-xiang.Image Fusion based on HSV Color Space Model and Wavelet Transform [J].Computer Engineering and Design,2007,28(23): 5682-5694.

[5] 南栋,毕笃彦,查宇飞,等.基于参数估计的无参考型图像质量评价算法[J].电子与信息学报,2013, 35(09):2066-2072.

NAN Dong,BI Du-yan,ZHA Yu-fei,et al.A No-reference Image Quality Assessment Method Based on Parameter Estimation[J].Journal of Electronics&Information Technology,2013,35(09):2066-2072.

[6] 郭雷,程塨,赵天云.基于小波变换和邻域特征的多聚焦图像融合算法[J].西北工业大学学报,2011, 29(03):454-459.

GUO Lei,CHENG Gong,ZHAO Tian-yun.A New and Effective Multi-Focus Image Fusion Algorithm Based on Wavelet Transforms and Neighborhood Features[J]. Journal of Northwestern Polytechnical University,2011, 29(03):454-459.

[7] 赵青,何建华,温鹏.基于平均梯度和方向对比度的图像融合方法[J].计算机工程与应用,2012,48(24): 165-168.

ZHAO Qing,HE Jian-hua,WEN Peng.Image Fusion Based on Average Grads and Wavelet Contrast[J].Computer Engineering and Applications,2012,48(24):165-168.

[8] 杨莎莎,田小平,吴成茂.基于小波变换的多聚焦图像自适应融合[J].西安邮电学院学报,2012,17(03): 24-29.

YANG Sha-sha,TIAN Xiao-ping,WU Cheng-mao. Multi-focus Image Fusion Scheme Based on Wavelet Transform[J].Journal of Xi’an Institute of Posts and Telecommunications,2012,17(03):24-29.

[9] NUNEZ J,OTAZU X,FORS O,et al.Multiresolutionbased Image Fusion with Additive Wavelet Decomposition [J].IEEE Trans on Geoscience and Remote Sensing, 1999,37(03):1204-1211.

LIU Yan-ying(1987-),female,graduate student,mainly engaged in digital signal processing.

凌朝东(1964—),男,教授,主要研究方向为集成电路设计,信号处理,生物医学电子学。

LING Chao-dong(1964-),male,professor,mainly engaged in IC design,signal processing,biomedical electronics.

Improved Multi-Focus Colour Image Fusion Algorithm based on Neighborhood

LIU Yan-ying1,2,LING Chao-dong1,2
(1.College of Information Science&Engineering,Huaqiao University,Xiamen Fujian 361021,China; 2.Key Laboratory of ASIC and System of Xiamen,Xiamen Fujian 361008,China)

Multi-focus color image fusion has the problems of color maldistribution and spot effect,an improved fusion algorithm is put forward,which separates spatial and color information of image.Firstly,the source images makes HSV transform and separates their components,then the V component representing space information decomposes wavelet,and the high frequency coefficients of the highest layer are fused adopting larger neighborhood contrast,while the other coefficients are selected based on neighborhood gradient weight.Then the V component is reconstructed,the H and S components,which reflect image’s color information,are fused by smaller Euclidean distance between source and fusion images’V component.Finally fusion image is achieved through HSV inverse transformation.Simulations in MATLAB indicate that the algorithm could effectively ease fusion image color maldistribution and spot effect phenomenon.

image fusion;color space transform;contrast;gradient weight

TN91

A

1002-0802(2014)06-0618-05

10.3969/j.issn.1002-0802.2014.06.007

刘艳英(1987—),女,硕士研究生,主要研究方向为数字信号处理;

2014-03-18;

2014-04-25 Received date：2014-03-18;Revised date：2014-04-25