布尔函数全局雪崩特征的两个新指标*

谯通旭,王 瑛,孙 瑞

(中国电子科技集团公司第三十研究所,四川成都610041)

布尔函数全局雪崩特征的两个新指标*

谯通旭,王 瑛,孙 瑞

(中国电子科技集团公司第三十研究所,四川成都610041)

ZHANG Xian-Mo和ZHENG Yu-liang提出单个函数f的全局雪崩特征的概念,并且给出单个函数雪崩特征的平方和指标σf与绝对指标Δf的上下界。周宇等将上面的概念作了推广,提出了两个函数f和g全局雪崩特征的概念。他们给出了两个函数全局雪崩特征的平方和指标σf,g与绝对指标Δf,g。进而定义两个新指标:λf(指g遍历所有n元布尔函数时,σf,g取得的最小值)和βf(指g遍历所有n元布尔函数时,Δf,g取得的最小值)。得到了λf的值,给出了λf和βf的上界和下界。

布尔函数 Walsh谱 全局雪崩特征 平方和指标 绝对指标

0 引 言

布尔函数是密码学中研究的对象之一。人们最先考察关于函数的严格雪崩准则[1-2](SAC)和扩散特征[3](PC)。ZHANG Xian-mo和ZHENG Yu-liang推广了这两个概念,提出了单个函数全局雪崩特征的概念[4]。它是整体上度量单个布尔函数的扩散特性。它以研究单个函数的自相关为基础。以两个函数的互相关为基础,周宇等提出了两个布尔函数的全局雪崩特征[5]。并且定义了平方和指标σf,g与绝对指标Δf,g。给定函数f,当g跑遍所有布尔函数时,σf,g有一个最小值λf,它意味着对任意的函数g,σf,g不可能小于这个值。因此,选g的时候,希望σf,g接近λf。同样,可以定义βf。以后可以看到,任给f,计算λf容易;计算βf通常要困难的多。应该综合地看待指标λf和βf。即构造f,使得指标λf和βf都较小。

1 准备工作

假定n≥2。为二元域上的n维向量空间。Bn为所有n元布尔函数的集合。设f(x)∈Bn,定义f的Walsh(循环)谱为

这里ωx=ω1x1+ω2x2+…+ωnxn。

能量守恒定理(也称为Parseval关系)如下:

函数f(x)与g(x)的互相关函数定义为

函数f(x)与g(x)的全局雪崩特征的平方和指标定义为

由文献[5]的推论2知道

这里G(ω)是函数g的Walsh(循环)谱。

函数f(x)与g(x)的全局雪崩特征的绝对指标定义为

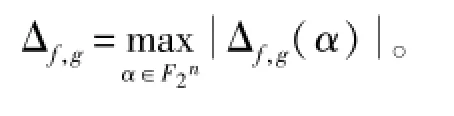
2 全局雪崩特征的两个新指标

定义1给定函数f∈Bn,定义,这里min表示最小值。

定义2给定函数f∈Bn,定义,这里min表示最小值。

定理1。

证明:对任何g,≥(根据能量守恒定理)。设,令g(x)=ω0x,则G(ω0)=2n;G(ω)=0,对所有ω≠ω0成立。因此,此时·。所以λf=2n·。

推论1①当n为偶数时,0≤λf≤22n。如果有一ω0满足F(ω0)=0,则λf=0。特别地,如果f为bent函数,则λf=22n。

②当n为奇数时,0≤λf＜22n。

定理20≤βf≤2n-2。

定理3若f是bent函数,则βf=。

实际上,有时有非仿射函数f和g满足Δf,g=。例如f为二次bent函数,h为二次以上的bent函数。g=f+h。f(x+α)+f+h为bent函数加上一个仿射函数。因此Δf,g=。

定理4λf=0等价于βf=0。

证明:按定义可证。

由定理3和定理4可求出βf,一般情况下求βf很难。λf和βf有时一致。猜测有时不一致。

猜测1存在f和g,满足λf＜λg,βf＞βg。

可用构造的方式或计算机搜索方式解决此猜测。

在密码学中,给定函数f,在选g时,尽量使σf,g接近λf,Δf,g接近βf。

3 结 语

提出了全局雪崩特征的两个新指标。一旦给定f,通过计算它的walsh谱,可以得到σf,g的最小值λf,这与周宇博士的方法(任给定f和g,计算σf,g)不同。在密码学中,如何使σf,g值小是大家关心的问题。给定f,如何计算指标βf是以后研究的目标。当然,还要综合考虑其它密码学指标[6-9]。在这些结论的基础上,可将单输出布尔函数推广为多输出布尔函数,或将有限域GF(2)推广为整数模q剩余类环Zq,再重新定义和计算σf,g。

[1] ADAMS C M,TRVARES S E.Generating and Counting Binary Bent Sequences[J].IEEE Transactions on Information Theory,1990,36(05):1170-1173.

[2] WEBSTER A F.Plaintext/Ciphertext Bit Dependencies in Cryptographic System[D].Ontario,Canada:Department of Electrical Engeneering,Queen’s University,1985.

[3] PRENEEL B,LEEKWIJC K,LINDEN LV,et al.Propagation Characteristics of Boolean Functions[C]//Advances in Cryptology-EUROCRYPT’90.Berlin:Springer -Verlag,1991:155-165.

[4] ZHANG X M,ZHENG Y L.GAC-the Criterion for Global Avalanche Characteristics of Cryptographic Functions [J].Journal for Universal Computer Science,1995, 1(05):316-333.

[5] ZHOU Yu,XIE Min,XIAO Guo-zhen.On the Global Avalanche Characteristics between Two Boolean Functions and the Higher Order Nonlinearity[J].Information Sciences,2010,180(02):256-265.

[6] 王林,谯通旭,赵伟,等.关于完全非线性函数的非线性度的界[J].信息安全与通信保密,2011(11):66-67.

WANG Lin,QIAO Tong-xu,ZHAO Wei,et al.On Nonlinearity Bounds of Perfect Nonlinear Functions[J]. Information Security and Communications Privacy,2011 (11):66-67.

[7] 谯通旭,祝世雄,王运兵,等.单圈T函数序列与M序列研究[J].信息安全与通信保密,2013(01):36-39.

QIAO Tong-xu,ZHU Shi-xiong,WANG Yun-bing,et al.Study on Single-Cycle T-Function Sequences and MSequences[J].Information Security and Communications Privacy,2013(01):36-39.

[8] 谯通旭,王运兵,谢上明,等.具有最大代数免疫度函数的研究[J].通信技术,2013,46(11):86-89.

QIAO Tong-xu,WANG Yun-bing,XIE Shang-ming,et al.Study on Functions with Optimum Algebraic Immunity [J].Communications Technology,2013,46(11):86-89.

[9] ZHOU Yu.On the Distribution of Autocorrelation Value of Balanced Boolean Functions[J].Advances in Mathematics of Communications,2013,7(03):335-347.

QIAO Tong-xu(1963—),male,B.Sci., senior engineer,mainly engaged in the research of cryptography.

王 瑛(1971—),女,硕士,高级工程师,主要研究方向为信息安全与通信保密;

WANG Ying(1971—),female,M.Sci.,senior engineer, mainly engaged in the research of information security and communications privacy.

孙 瑞(1982—),男,学士,工程师,主要研究方向为密码学及其应用。

SUN Rui(1982—),male,B.Sci.,engineer,mainly engaged in the research of cryptography and its applications.

Two New Indicators of Global Avalanche Characteristics between Two Boolean Functions

QIAO Tong-xu,WANG Ying,SUN Rui
(No.30 Institute of CETC,Chengdu Sichun 610041,China)

ZHANG Xian-Mo and ZHENG Yu-liang suggested the notion of global avalanche characteristics of single Boolean functionf,and introduced the sum of squares indicatorσfand the absolute indicator Δf. ZHOU Yu et al.generalized the above notions.The notion of global avalanche characteristics of two Boolean functionfandgis proposed,and the sum of squares indicatorσf,gand absolute indicatorΔf,gof global avalanche characteristics of two Boolean functionfandgare defined.Givenn-variable functionf,λf, which is minimum value ofσf,g,wheregis anyn-variable Boolean function,is defined.βf,which is minimum value of Δf,g,wheregis any n-variable Boolean function,is defined.These are two new indicators.λfis computed.The lower and the upper bounds ofλfandβfare given.

boolean function;walsh spectrum;global avalanche characteristics;sum of squares indicator; absolute indicator

TN918.1

A

1002-0802(2014)06-0651-03

10.3969/j.issn.1002-0802.2014.06.014

谯通旭(1963—),男,学士,高级工程师,主要研究方向为密码学;

2014-04-14;

2014-05-13 Received date：2014-04-14;Revised date：2014-05-13

国家自然科学基金(No.61309034);中国电子科技集团创新人才项目(No.JJQN201332)

Foundation Item:National Natural Science Foundation of China(No.61309034)and China Electronics Technology Group Corporation Innovative Technology Projects(No.JJQN201332)