改进的ECC算法在数字认证中心系统应用
刘 军, 贾松浩, 杨 彩
(南阳师范学院 计算机与信息技术学院,河南 南阳 473061)
0 引 言
安全性高、算法实现性能更好的椭圆曲线公钥系统[1](Elliptic Curve Cryptography,ECC)是基于离散对数问题,使用的是有限域上椭圆曲线的有理点群[2]。但是至今人们尚未找到有限域上椭圆曲线上有理点群的离散对数问题的亚指数算法[3],而且目前的研究结果表明构造出这样的亚指数算法的可能性不大[4]。近20年的公钥密码和相关数论的研究表明,研究整数分解问题的一个进展往往可以被改造用来研究离散对数问题,因为这两个问题的难解程度被认为相当[5]。因此,可以利用已知的最好算法解决的整数分解问题来处理离散对数问题和椭圆曲线离散对数问题[6]。ECC比RSA的每比特所蕴涵的安全性 (比特级安全性)要高很多,而且随着密钥规模的扩大,这种比特级安全性的优势在扩大[7]。
1 椭圆曲线的加/解密
假设用户A欲将明文m加密后发送给B,A需执行以下的操作:① 用户A选定一条椭圆曲线E,并取椭圆曲线上一点作为基点G;② 用户A选择一个私有密钥k,并生成公开密钥K=kG;③ 用户A将E、点G和公开密钥K传给用户B;④ 用户B接到信息后,将待传输的明文编码到E上一点M,并产生随机整数r(r 图1 椭圆曲线加/解密示意图 根据已有的椭圆曲线数字签名算法,本文做了进一步的改进,使其运算负担减少、速度提高[8]。在现有的椭圆曲线加密或者签名过程中,求逆是主要的运算负担,如在验证签名中,w=s-1(modn)这个运算是很慢的,在此构造一种新的签名方程,在改进的ECC算法的计算过程中不需要求逆的步骤,因此效率较高[9]。具体阐述如下:① 签名者确认Hash函数,以生成信息摘要;② 签名者确定椭圆曲线参数F=(P,a,h,g,n,h)或(m,f(x),a,h,g,n,h);③ 签名者向验证者传送所确定的Hash函数,椭圆曲线域参数;④ 签名者在有限域G(P)与椭圆曲线点群选定的基础上选择密钥x,由公开基点g得公钥y=xg并公开y;⑤ 签名者选随机数K,1≤K≤n-1;⑥ 计算r=kg,如果r=0,则转向第⑤步;⑦ 计算s=mrx-k;⑧ 所得(s,r)作为对m的签名,并将(s,r)连同m发送给验证者;⑨ 验证者计算r′=sg+mry的值;⑩ 验证者判断r′=r,相等则签名成立,否则拒绝签名。 改进的算法减轻了运算的负担,提高了整个运算速度,这种方案在提供相同安全性的前提下,对系统资源的要求更低,更有实用价值[10]。 本系统设计时,提供公共接口,满足系统的可扩展性,为用户发布两种不同功能类型的数字证书:签名证书和加密证书,可以保证更好的安全性[11]。数字认证中心系统采用MVC结构,采用JAVA EE实现,使用SQL Server2005数据库存储各种信息[12]。服务器端实现了CA(Certificate Authority)中心的操作,采用图形化界面,其操作简单易用,实现了一个认证中心系统的全部功能。 数字认证中心系统的设计过程中,对CA的结构进行简化和补充:① 考虑到本文研究认证中心CA时,侧重于对非对称加密算法的加密和签名的应用,因而涉及用户使用的证书数量较少,并且涉及实现的认证功能相对简单。在本系统在实现中,CA同时完成RA(Register Authority)的功能,CA发布证书。② 本系统涉及到两个数据库:一是证书库,存储了用户的信息、用户的证书信息和撤销列表信息等;二是私钥库,是对用户私钥的备份。系统结构如图2所示。 图2 数字认证中心系统的结构 其中,CA后台管理实现了一个认证中心CA的证书颁发、证书查询、证书更新和证书撤销等全部功能;系统客户端实现的是证书拥有用户对数字证书的各种操作。 公钥证书即是一个用户的公钥和他的身份的绑定,在绑定前由一个可以信任的证书权威机构(CA)来证实用户的身份,然后这个可信任CA对证明该绑定的证书进行数字签名。基于ECC公钥体制中,如果一个用户想要申请一个证书,将采取下列步骤:① 任何人(如用户A)想要申请证书必须个人向CA申请,因为CA要检验这个人的身份。 ② 用户A可以直接向计算机输入他的个人信息与相应的口令。③ CA存贮这些数据到一个临时目录。④ 在这个阶段,将生成一个密钥对(随机生成一个私钥s及与其相对的公钥S=sG)。⑤ 生成密钥对后,发送这个公钥(一个椭圆曲线上的点)到CA服务器。⑥ CA对用户A的公钥及其它一些与该用户有关的信息,如个人姓名、电子邮件地址等进行数字签名,形成一个数字证书。⑦ 生成证书以后,CA负责把该证书拷贝到智能卡中,发送给用户A。 数字认证中心系统CA的根证书和私钥是所有CA系统的核心。用户的证书信息和公钥信息都是需要经过CA的私钥进行签名,CA的数字签名和算法是数字证书的重要内容。用户验证时,必须拥有CA的公钥才能解开证书中的CA签名,所以也必须在浏览器中先安装CA根证书,得到CA的公钥。有了数字认证中心系统的根证书和私钥,就可以颁发证书和对证书进行各种操作。 (1) 证书颁发模块。颁发证书的过程是一个将审核通过的用户申请信息经过复杂的编码、解码和签名的过程。证书颁发的流程如图3所示。 图3 证书颁发的流程 (2) 证书撤销模块。在证书有效期内,数字认证中心系统接受用户申请或按照有关国家机关要求废除证书。证书作废后认证中心都需要对证书撤销列表进行更新及维护。 (3) 证书查询模块。证书查询包括查看所有已颁发的证书信息、查询特定的用户证书和证书撤销列表信息。按照一定的查询条件从数据库表中查询出CA签发的用户证书信息,为管理员进行查看或其它操作提供参考。查看所有已颁发的证书信息和查询特定的用户证书时,可查询数据库表。 (4) 证书更新模块。认证中心CA所产生的证书都有一定的有效期限。所有证书中都有明确的证书生存期,表明该证书的产生日期与失效日期。用户应在证书过期前更换新证书并在数据库中做相应的更改。本数字认证中心系统采用人工更新证书的方法,在证书将要到期前,管理员发Email提示用户证书将要到期,是否需要更新证书,用户向认证中心提交更新请求,管理员审核合格后向CA发出签发请求,CA颁发新证书后将证书送到认证中心,管理员发Email通知用户证书已成功更新,用户可到指定的网址去下载自己的新证书。在证书更新时,不需要再次审核用户信息,本系统的证书更新过程是在撤销原有证书的基础上,为用户重新颁发证书[13]。 由于计算量小和处理速度快,改进ECC的实现可以选取比RSA小得多的大数,实现速度要比RSA、DSA快得多。存储空间占用小,密钥尺寸和系统参数与RSA、DSA相比要小得多。160位ECC与1 024位RSA、DSA具有相同的安全强度。 改进ECC算法的安全性基于椭圆曲线点群上离散对数问题(ECDLP)的难解性,基于模运算的整数因式分解问题和离散对数问题是存在亚指数时间复杂度的运算法。同时,改进ECC把实数域上的乘法运算、指数运算等映射成椭圆曲线上的加法运算,比其他公钥密码体系更快,更容易实现,成本更低。 改进ECC算法还具有一些更高级的安全特性,如在设计前向保密的密码方案、抵抗密码实现中的计算错误等方面比RSA具有优势。 为了解决数字认证中心系统的安全认证问题,研究了 ECC算法,并和RSA算法、DSA算法进行了安全性分析和比较。把改进的ECC算法运用到数字认证中心系统的实现过程中,设计了一个认证中心CA——数字认证中心系统,实现数字证书的管理功能:证书的颁发、证书的更新、证书的查询和证书的撤销等功能,能够比较完整的实现一个用户从最初的注册到获得数字证书,到对拥有证书进行各种操作的过程。同时,本系统为用户发布两种不同功能类型的数字证书:签名证书和加密证书。算法分析说明改进的ECC算法安全性更好,更容易实现,成本也更低。 [1] 秦志光. 密码算法的现状与发展研究[J]. 计算机应用, 2004, 24(2):3-4. QIN Zhi-guang. Cryptography Algorithm—Survey Trends[J]. Computer Applications,2004,24(2):3-4. [2] 姬 睿,申 辉. 基于信息安全领域的密码技术[J].实验室研究与探索, 2010,29(9):67-72. JI Rui, SHEN Hui.The Research of Public-key Cryptography in Information Security Teachnology[J].RESEARCD AND EXPLORATION lN LABORATORY, 2010,29(9):67-72. [3] 刘 铎,戴一齐.计算椭圆曲线上多标量乘的快速算法[J]. 计算机学报,2008, 31(7):1131-1138. LIU Duo, DAI Yi-qi. A New Algorithm of Elliptic Curve Multi-Scalar Multiplication[J].CHINESE JOURNAL OF COMPUTERS, 2008, 31(7):1131-1138. [4] 宁国强,李谢华,尹张飞.一种安全的即时通信解决方案[J]. 计算机工程与应用,2011, 47(3):82-83,93. NING Guo-qiang, LI Xie-hua, YIN Zhang-fei. Solution to secure instant messaging[J].Computer Engineering and Applications,2011,47(3):82-83,93. [5] 李 楠,谷 山,苏锦海. SAKI方案的分析及改进[J]. 计算机工程,2010,36(23):116-118. LI Nan, GU Shan, SU Jin-hai. Analysis and Improvement of Separable and Anonymous Identity-based Private Key Issuing Scheme[J]. Computer Engineering,2010,36(23):116-118. [6] 刘 巧,彭新光.基于ECC的嵌入式系统的一次性口令方案[J].计算机工程与设计,2013,34(4):1212-1216. LIU Qiao, PENG Xin-guang. One-Time Password Scheme of emhedded system based on ECC[J].COMPUTER ENGINEERING AND DESIGN,2013,34(4):1212-1216. [7] 李 浪,杨 柳,李肯立,等.一种椭圆曲线密码算法ECC旁路攻击方法研究[J].计算机应用研究,2013,30(3):889-890. LI lang, YANG Liu, LI Ken-li,etal. Research on side-channel attack methods of ECC[J].Application Research of Computers,2013,30(3):889-890. [8] 魏先民. 改进的ECC算法在网络信息安全中的研究[J].计算机科学,2013,40(1):136-138. WEI Xian-min. Research on Improved ECC Algorithm in Network and Information Security[J].Computer Science, 2013,40(1):136-138. [9] 肖自金,周 海,吴丽珍. 基于椭圆曲线ElGamal代理加密机制的MANET组密钥分发方案[J].计算机应用与软件,2013,30(3):139-144. XIAO Zi-jin, ZHOU Hai, WU Li-zhen. A New ECC Elgamal Proxy Eneryption-based Group Key Distribution Scheme for Manet[J].Computer Applications and Software, 2013,30(3):139-144. [10] 吴学慧,牛志华,王 潮. 基于椭圆曲线密码的RFID安全协议[J]. 计算机工程与设计,2010, 31(24): 5165-5167,5182. WU Xue-hui, NIU Zhi-hua, WANG Chao. Security protocol of RFID based elliptic curve cryptography[J].Computer Engineering and Design, 2010, 31(24): 5165-5167,5182. [11] 刘 淳,张凤元,张其善.基于智能卡的RSA与ECC算法的比较与实现[J]. 计算机工程与应用,2007,43(4):96-98,118. LIU Chun, ZHANG Feng-yuan, ZHANG Qi-shan. Comparing and implementation of ECC and RSA algorithms on Smartcard[J]. Computer Engineering and Applications, 2007,43(4):96-98,118. [12] 康鸿雁.基于ECC的RFID组证明协议分析及改进[J]. 计算机工程,2013,39(1):153-156,163. KANG Hong-yan. Analysis and Improvement of Grouping-proof Protocol for RFID Based on ECC[J]. Computer Engineering, 2013,39(1):153-156,163. [13] 姚剑波,张 涛. 抗侧信道攻击的安全有效椭圆加密算法[J]. 计算机应用研究,2012,29(12):4639-4643. YAO Jian-bo, ZHANG Tao. Safe and effective elliptic encryption algorithm resistance against side-channel attack[J]. Application Research of Computers, 2012,29(12):4639-4643. [14] 杨同豪,郁 滨. 基于身份的ZigBee节点认证方案[J]. 计算机工程与设计,2012,33(11):4127-4130. YANG Tong-hao, YU Bin. Identity-based authentication Scheme for ZigBee nodes[J]. Computer Engineering and Design, 2012,33(11):4127-4130. [15] 陈丹伟,薛青晗,章 韵. 基于ECC的RDP认证机制研究[J]. 南京邮电大学学报(自然科学版),2012,32(5):32-37. CHEN Dan-wei, XUE Qing-han, ZHANG Yun. Research of RDP authentication system based on ECC[J].Journal of Nanjing University of Posts and Telecommunications(Natural Science), 2012,32(5):32-37.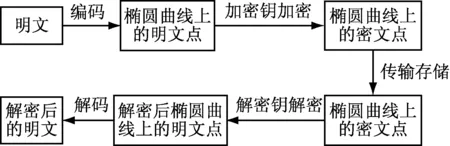
2 改进的ECC算法
3 算法在数字认证中心系统的应用
3.1 数字认证中心系统的结构
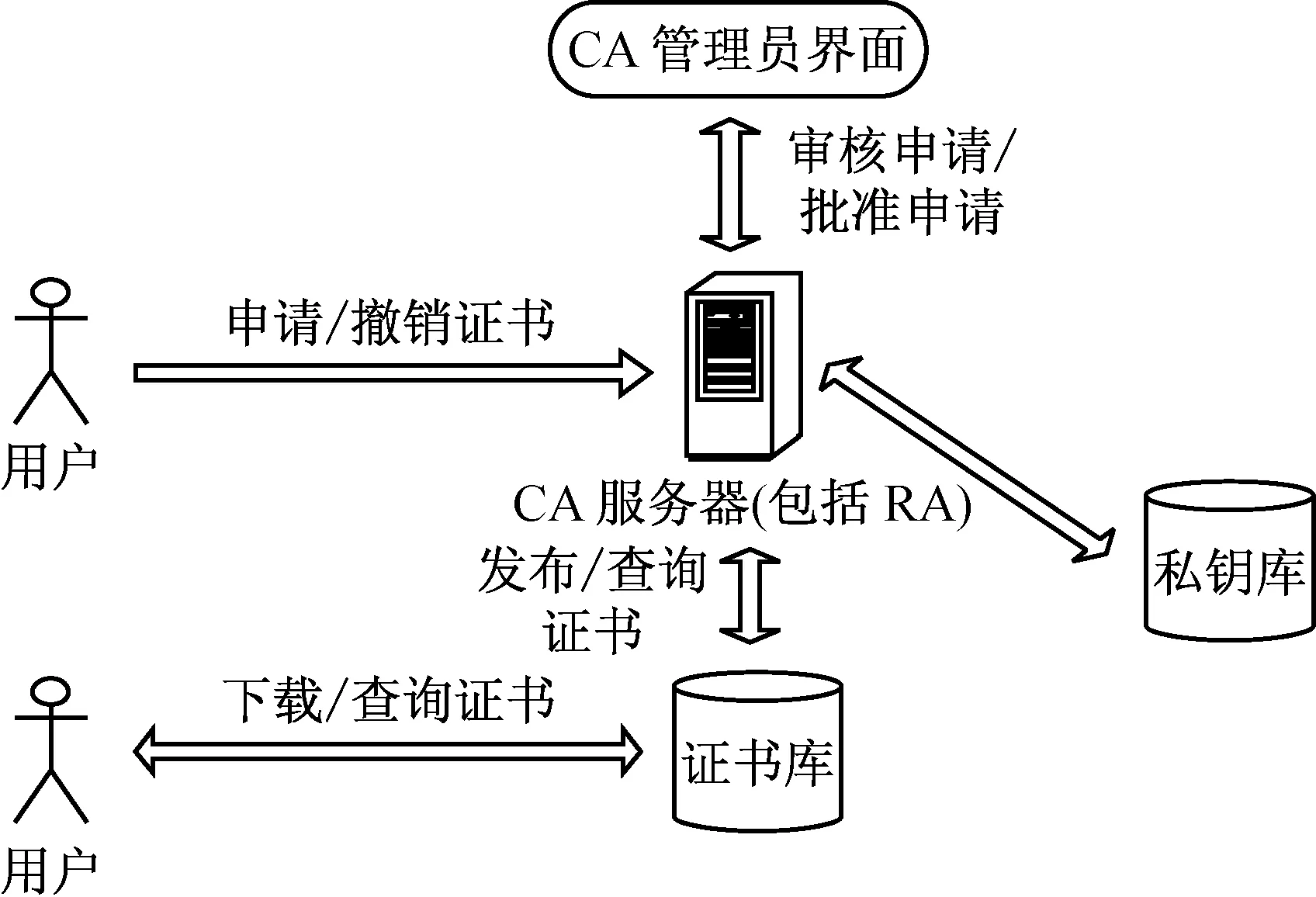
3.2 基于算法的证书请求与生成
3.3 认证中心各模块的设计与实现
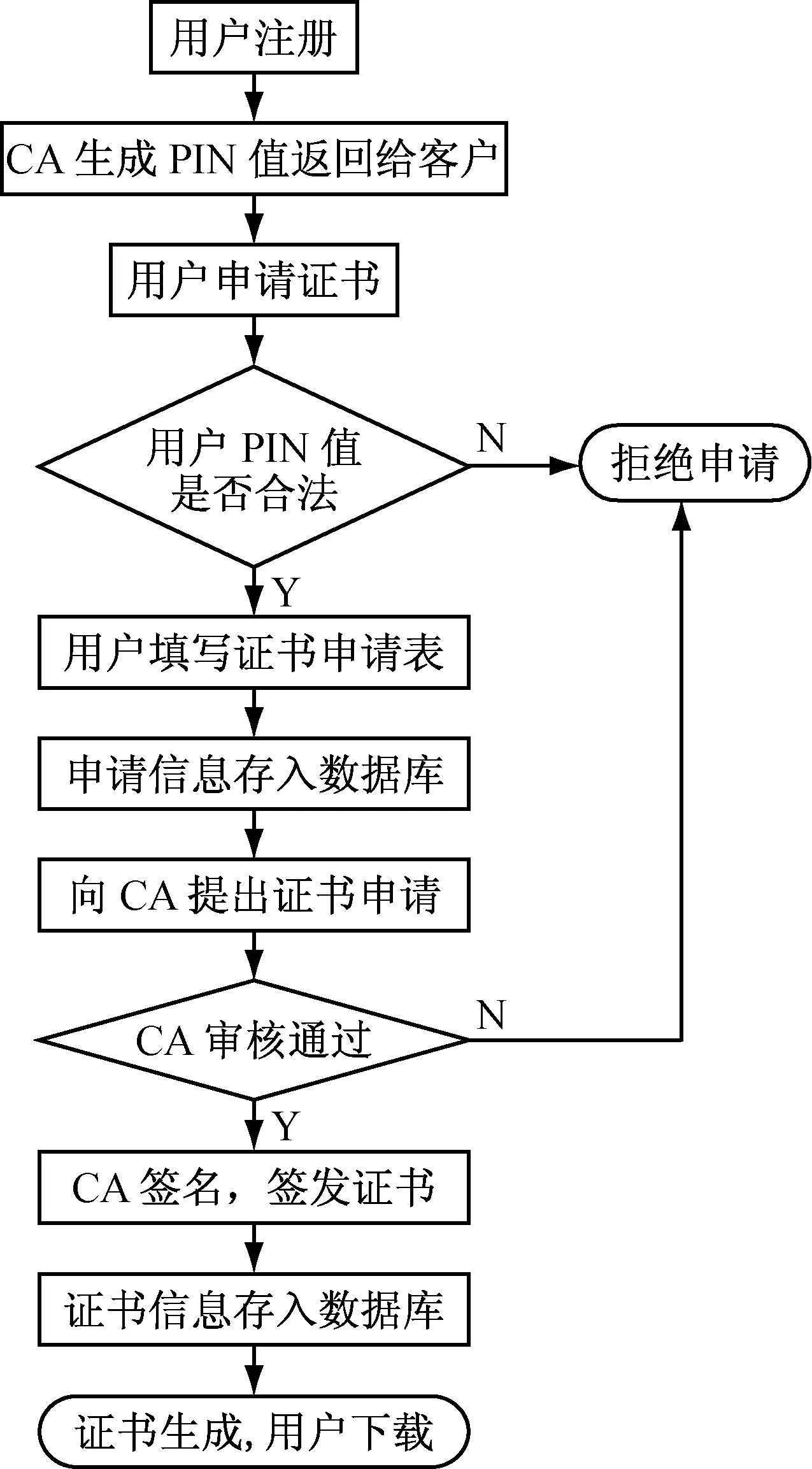
3.4 安全性分析

4 结 语

