一个基本电路的拓展

尹春军

（嘉兴一中实验学校，浙江嘉兴314050）

一个基本电路的拓展

尹春军

（嘉兴一中实验学校，浙江嘉兴314050）

本文抓住了一个基本电路这个电学“牛鼻子”，从静态分析到动态变化、逐步拓展、由浅入深，进行四种变换分析，理清了电压法、电流法、伏安法测电源电动势和内阻的来龙去脉，给出了系统误差分析方法及对电路保护的处理技巧。对更好的把握物理教学的本质有一定的借鉴意义。

“牛鼻子”；拓展；分析；误差分析

不论是学习还是教学，都要抓住学科精髓，也就是学科的“牛鼻子”。高中物理选修3-1的闭合电路欧姆定律的“牛鼻子”就是一个基本电路（如图1，电压表、电流表看作理想电表），只要“理通”这个电路中涉及的各个物理量之间的关系，就把握了这一节的精髓。下面就具体解析这个“牛鼻子”。

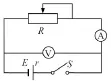
图1

从闭合电路来看：滑动变阻器和电源串联，电源电动势被滑动变阻器和内电阻分担，即：E=UR+Ur，电压表测路端电压，电流表测干路电流，即：I=E/（R+r）。这就弄清了闭合电路欧姆定律的电压分配关系和电流与电压、电阻的关系。这是一个静态分析。

动态分析一：如图1，如果把滑动变阻器触头向右移，问电压表的读数如何变化？我们不难得到，进一步变形就可以得到，可见滑动变阻器触头向右移，外电阻R增大，也增大。

拓展：以上不仅分析了这个动态变化，也得到了路段电压U和电阻R的函数关系，即：。对于一个闭合电路而言，如果知道两组U和R的值，就可以求出这个闭合电路电源的电动势E和内阻r。根据这个原理把图1的电路图变形为图2，就变成了电压法测电源电动势和内阻了。

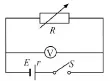
图2

进一步思考一：如何更方便用图像法处理数据呢？我们可以把变形为，根据实验数据作出和的函数图像即为一次函数图像（图3），图像的纵坐标截距为，斜率为，横坐标截距为，所以根据图像就很容求出E和r了。

进一步思考二：实验中的电压表实际上不是理想电表，由于电压表的分流导致了实验系统误差。如果考虑电压表的内阻，

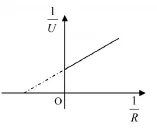
图3

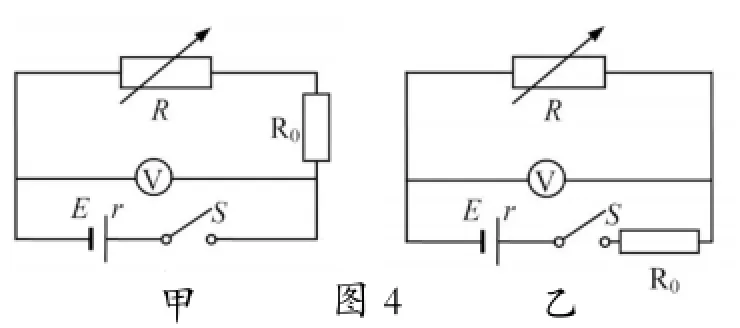
进一步思考三：基于对电路安全的考虑，可对图2的电路图加一保护电阻R0，如图4的甲和乙。对甲图处理数据时需画和图像，由图像得到的是电源电动势和内阻的测量值。对图乙处理数据时需画和图像，由图像得到的是电源电动势的测量值及电源内阻r及保护电阻R0之和的值。只要知道保护电阻R0就不难得到电源内阻r的测量值。

动态分析二：如前图1，如果把滑动变阻器触头向右移，问电流表的读数如何变化？由闭合电路欧姆定律我们不难得到，可见当滑动变阻器触头向右移时，电阻R增大，电流I减小。

拓展：动态分析二中也给出了电流I和电阻R的函数关系，理论上只要知道两组电流和电阻值，就可以求出电源电动势和内阻。根据这个原理，把电路图1改变成电路图5，就是电流法测电源电动势和内阻了。

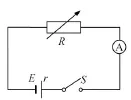
图5

进一步思考一：在数据处理上也可以采用前述的图像法。为了方便我们需作出图像（如图6），图像的斜率即为，横坐标截距为，纵坐标截距为，我们很容易测出电源电动势E和内阻r了。

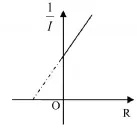
图6

进一步思考二：由于实验时电流表不是理想电表，而是有内阻的，这样由于电流表分流导致出现系统误差。如果考虑电流表的内阻得，由此可见：图像（如图6）的斜率应为，横坐标截距应为，纵坐标截距应为，通过比较可得：，，不过由于电源内阻较小，内阻测量误差就较大了。当然为了电路的安全，也可以给电路加一个保护电阻。

动态分析三：如前图1，如果把滑动变阻器触头向右移，由前面分析可知路端电压U增加，干路电流I减小，U和I必遵守。

拓展：根据动态分析三可知只要知道两组U和I就可以测出电源电动势和内阻了，这就是我们非常熟悉的伏安法测电源电动势和内阻。为了减小误差可以采用图像法处理数据：图（图7）中纵坐标截距为E，斜率为，横坐标截距为短路电流。

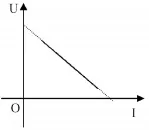
图7

进一步思考：由于电压表和电流表是实际电表，由于自身的分流或分压会导致系统误差，下面就电流表外接（如图8）探讨一下系统误差。

误差分析一——计算法

电流表外接的电路如图8所示,由于电压标的分流，测得的电流并不是通过电源的电流，采用这种接法时，电动势和内阻的测量值和真实值之间又有什么关系呢？

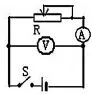
图8

设滑动变阻器的滑片在某一位置时电路中的电流表的示数为I1,电压表的示数为U1,改变滑片的位置，电流表中的示数为I2,电压表的示数为U2

由闭合电路的欧姆定律得：如果不考虑电表的影响则有E=U1+I1r①E=U2+I2r②

解得：

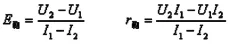
如果考虑电表的影响，设电流表的内阻为RV则有

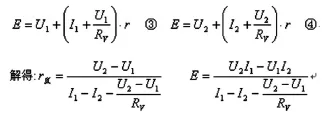
误差分析二——图像法

如图8，闭合电路的欧姆定律U=E-Ir中的I是通过电源的电流，而图8电路由于电压表分流存在系统误差，导致电流表读数（测量值）小于电源的实际输出电流（真实值）。设通过电源电流为，电流表读数为，电压表内阻为，电压表读数为U，电压表分流为，由电路结构，U越大，越大，U趋于零时，也趋于零。它们的关系可用图9表示，由测量数据画出的U-I图角为图象AB。根据修正值，图线上每点电压对应电流的真实值大于测量值，作出修正之后的U-I图线CB。由图象可看出图线AB的纵轴截距（）小于图线CB的纵轴截距（），图线AB斜率的绝对值（）也小于图线CB斜率的绝对值（），因此，E、r的测量值均小于真实值。

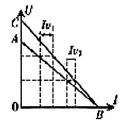
图9

误差分析三————等效法

，产生的相对误差也可以根据等效电源的方法进行定量计算，把变阻器的阻值R看成外电路的电阻，电压表看成内电路的一部分，如图10虚线框所示，由电压表和电源构成等效电源，E、r的测量值即为等效电源的电动势和内阻。

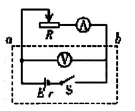
图10

②电流表的读数为等效电源的输出电流，外电路断开时a、b两点间电压Uab即等效电源开路电压为等效电源的电动势，即为电源电动势的测量值。等效电动势小于电源电动势，相对误差为，因为，所以相对误差很小，也满足实验误差允许范围。

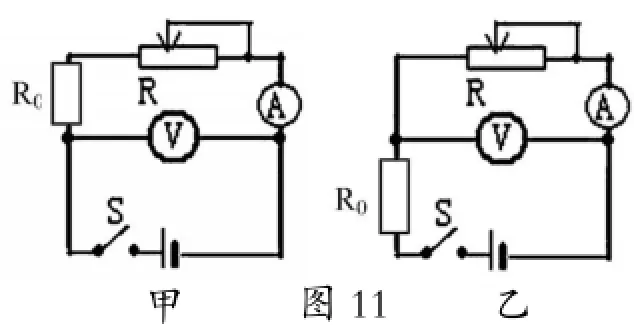
进一步思考二：考虑到电路的安全性，我们也可以采用加一个保护电阻R0，可以采用图11的甲、乙两种接法。不过乙图测量的内阻值实际上是R0和电源内阻r的和。

动态分析四：如前图1，如果把滑动变阻器触头向右移，由前面分析可知路端电压U增加，干路电流I减小，那么电源的输出功率如何变化呢？设电源电动势为ε，内阻为r，电源的外电路电阻为R，则电源的输出功率为：，可以利用数学上求极值的方法,对式子进行变换,使得分母在一定条件下有最小值,此时得出功率的最大值。当R=r时，输出功率P取极大值：，此时电源的效率为：η=0.5。那么可以得到当外电阻增大时，电源输出功率先增大后减小（如图12）。

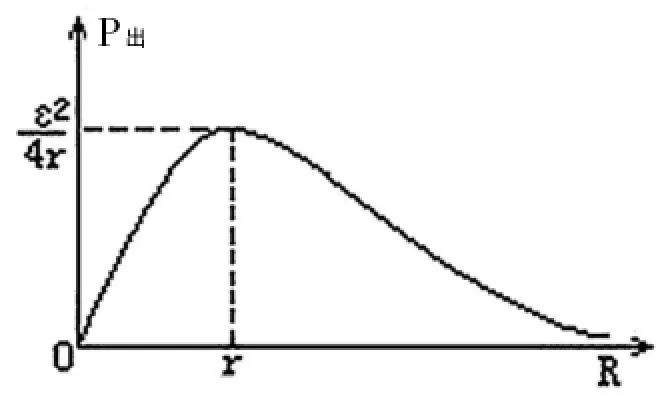
图12

通过以上四种动态变换分析我们可以看出，在物理教学实践过程中巧妙抓住知识的“牛鼻子”，进行合理有效的拓展，往往更能理清知识的脉络，可以更好的帮助学生对知识进行构建，这也许就叫“事半功倍”吧！

编辑∕高伟

尹春军（1975－），男，中学一级，主要研究方向：高中物理教学。U和R的函数关系式为：，那么图3中的纵坐标截距应为，斜率应为，横坐标截距应为，从而的出电源电动势和内阻的真实值，即和；而不考虑电压表内阻，根据得出的是电动势和内阻的测量值，即纵坐标截距为，斜率为，横坐标截距为。那么通过对比可见：，。