基于黏弹性本构性能的隧道围岩变形预测研究

俞文生 ，平 洋

（1.长沙理工大学，道路结构与材料交通行业重点实验室，长沙 410004；2.江西省高速公路投资集团有限责任公司，南昌 330025；3.山东大学岩土与结构工程中心，山东 济南 250061）

1 引 言

隧道开挖后洞周围岩发生的应力重分布而引发的洞周变形实际上是一个长期的过程。围岩变形过程中，不仅岩体的形状和内部结构不断发生变化，其应力状态也随之不断调整。岩石的流变变形是导致岩体地下隧道工程中支护结构产生变形和破坏的主要原因，对岩石流变特性的研究是在隧道工程中合理地选择支护类型及设计支护结构的前提[1]。

Griggs[2]1939年对灰岩、页岩和砂岩等岩石进行了蠕变试验，之后的几十年里，很多研究者相继从不同方面研究岩石流变特性。Wawersik[3]采用三轴流变仪，对含有人工节理面的圆柱体花岗岩试样进行了剪切流变试验。Amadei 等[4]进行了一系列节理面的三轴和剪切流变试验，岩性包括花岗岩、砂岩、石灰岩以及大理岩，探讨了剪应力比对流变特性的影响。Okubo 等[5]采用自行研制刚性试验机，进行大理岩、砂岩、安山岩和花岗岩的单轴压缩曲线的全过程测试，获得了岩石蠕变阶段的应变-时间关系曲线，提出了可描述岩石3 阶段流变的本构方程[5]。Maranini 等[6]对石灰岩进行了单轴压 缩和三轴压缩蠕变试验，研究结果表明流变的变形机制主要是由于低围压下裂隙扩展和高应力下孔隙塌陷所致。徐平等[7]采用了对数型经验公式对花岗岩的蠕变试验结果进行了拟合。来结合等[8]采用双面直推式剪切流变仪，对锦屏电站的绿片岩结构面进行了剪切流变试验，利用西原模型模拟了其蠕变特性，通过数值方法得出了模型的蠕变参数。郝哲等[9]利用圆形断面以及鲍埃丁-汤姆逊模型，研究洞室的几何模型及力学模型简化，讨论了洞室围岩物理参数的反分析。杜丽惠等[10]采用Vogit 三要素模型，建立了考虑开挖、衬砌施工过程的轴对称非线性有限元模型，并考虑了围岩的蠕变特性。

自1971年Kvanagah 等[11]提出反算弹性模量的有限元法以来反演方法发展很快，1976年Kirste[12]提出由实测岩体变形反算岩体弹性模量，1977年Maier 等[13]则从模型识别角度进行位移反分析的探讨。我国反分析的研究始于20 世纪70年代末，基本上与国际同步，国内学者在反分析方面的研究，无论理论研究还是工程实际应用方面都作出了独特的贡献。杨志法等[14]1978年开始反分析的研究，取得了很有价值的研究成果，提出了平面应变问题的有限元位移反分析法，并将反演标准化，适用于反分析的量测方法、应力反分析、应变反分析与位移-应变混合反分析等课题进行深入研究，取得了一系列成果。冯紫良等[15]1983年也进行初始地应力的位移反分析，对弹塑性问题和黏弹性问题的反演计算方法、优化反演理论、模型识别和初始地应力场回归分析等作了深入研究，并在多个岩土工程应用中讨论了数据处理方法和计算模型的工程简化。但是，对于变形预测方法及其准确性，仍然是个需要探讨的问题。

本文针对Ⅲ、Ⅳ级围岩，以江西高速公路隧道为背景，结合室内剪切流变试验，采用弹-黏塑性有限单元法，分析预测不同类别隧道围岩变形，研究成果已应用于江西高速公路隧道工程中，并指导和修正了施工设计。

2 室内剪切流变试验

2.1 试验概况

试验岩样取自江西高速公路隧道，为Ⅲ、Ⅳ级围岩岩样，见图1。开始流变试验之前，按常规试验方法测定岩石力学性质参数，并以此作为蠕变试验的参考值，再参考勘察资料和现场试验的基础上获得的岩石力学参数，见表1。

图1 岩样Fig.1 Rock samples

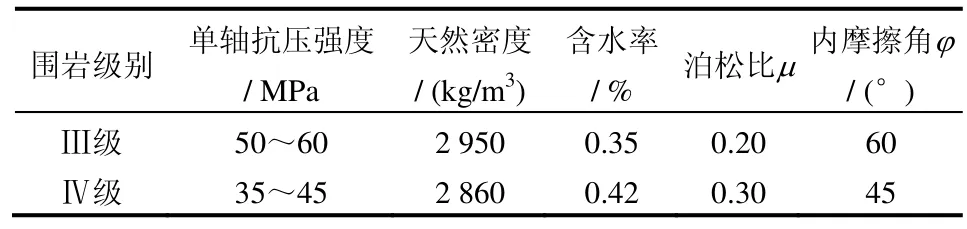
表1 岩样力学参数值Table 1 Mechanical parameters of rock samples

试验采用长春试验机研究所生产的岩石双轴流变试验机（见图2）进行岩石、混凝土在双轴压缩条件下的蠕变、剪切试验、单向拉伸蠕变试验，亦可进行应力松弛试验。岩石流变试验机出力稳、精度高、试验数据可靠。

图2 双轴流变试验机Fig.2 Biaxial rheological testing machine

2.2 试验加载方案

剪切流变试验的加载方案：（1）施加正应力，待正向变形稳定后施加剪应力，下同；（2）剪应力分3～5 级加载，直至岩样破坏；（3）每施加一级荷载时，每间隔一定时间读取数据一次；（4）变形稳定的标准是剪切位移速率小于5×10-4mm/d；（5）待岩样即将破坏时小心加载，免施加荷载过大使岩样突然破坏。剪切流变试验岩样概况及加载方案见表2。

表2 试验岩样概况及加载方案Table 2 Rock samples and loading schemes

2.3 试验结果

如图3 所示，Ⅲ、Ⅳ级围岩具有瞬弹性和黏弹性共存的特性，瞬弹性应变值随着应力水平的增加而增大。Ⅲ、Ⅳ级围岩在弹性变形后经历短暂的蠕变阶段，随即进入变形稳定阶段，破坏前无明显征兆，表现为脆性破坏。

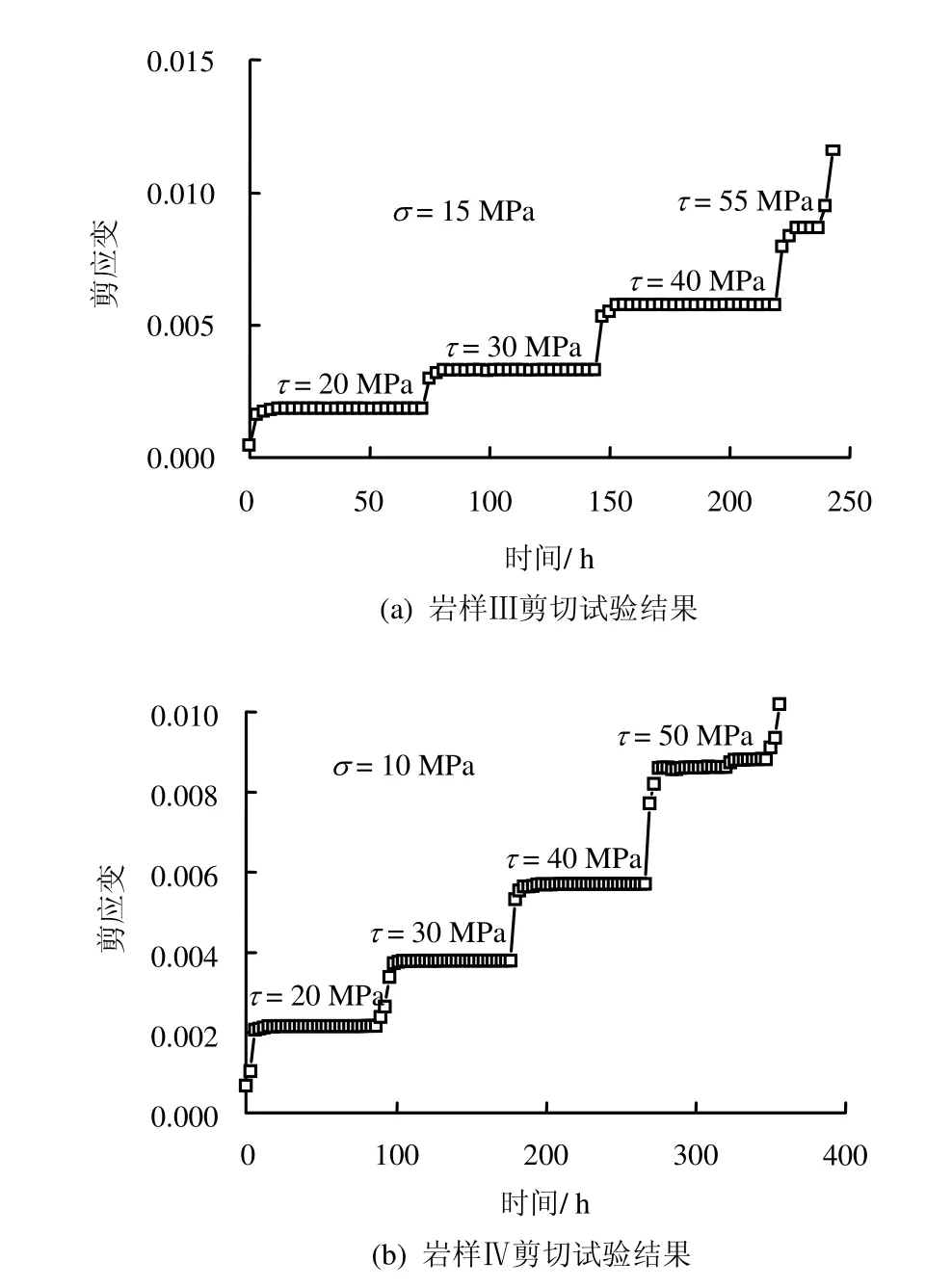
图3 剪切试验结果Fig.3 Shear test results

经过分析变形特点，选用广义Kelvin 模型（见图4）对其进行拟合分析。对岩石试样的流变力学模型进行辨识得到岩石试样蠕变参数，见表3。

根据拟合所得参数可以很容易的得到广义Kelvin 模型的流变曲线，图5为岩样Ⅲ、Ⅳ流变试验曲线与广义Kelvin 模型[16]的流变曲线的比较，可见吻合较好。

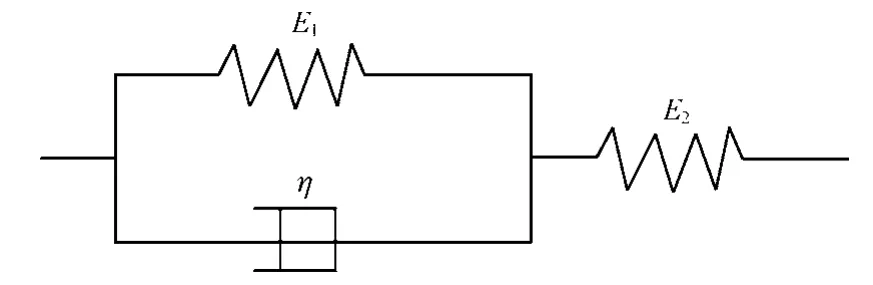
图4 Kelvin 模型Fig.4 Kelvin model

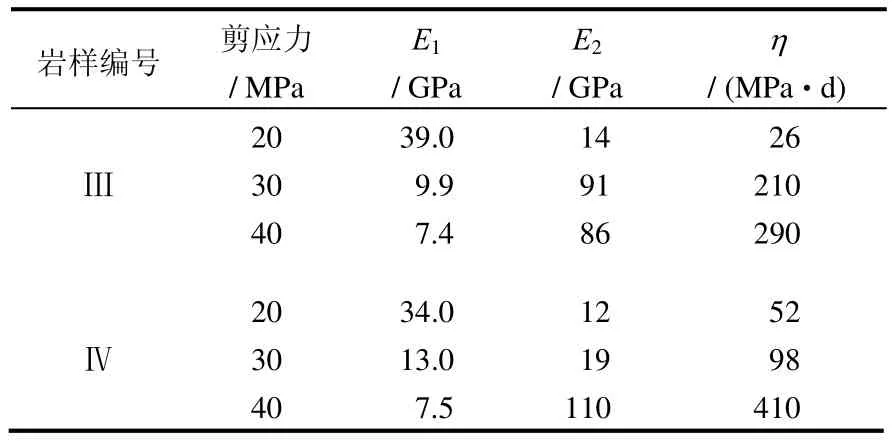
表3 广义Kelvin 模型拟合参数Table 3 The fitting parameters of generalized Kelvin model

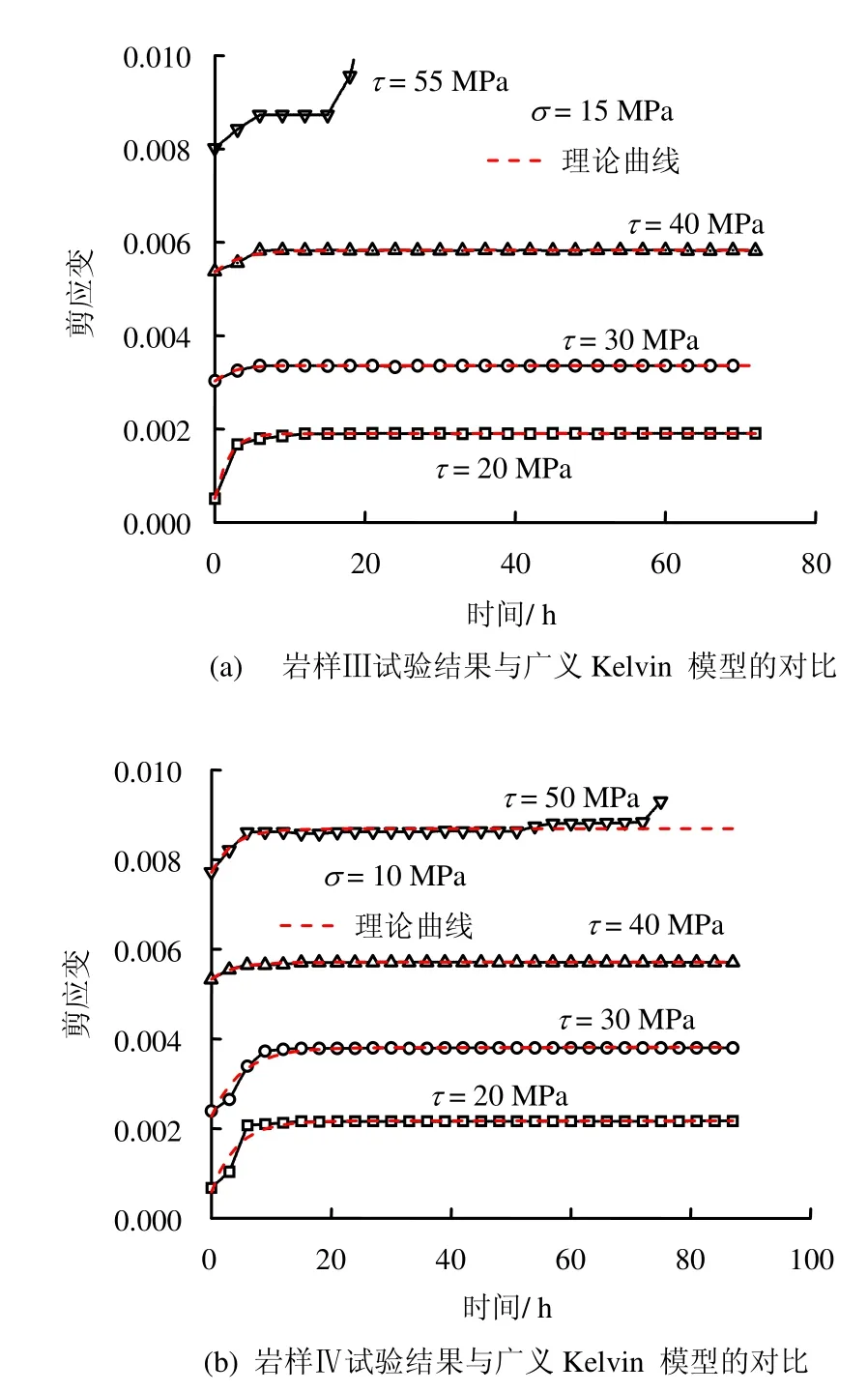
图5 试验与广义Kelvin 模型结果对比Fig.5 Analyzing results comparison of experiments and generalized Kelvin model

3 黏弹性本构方程

在任一微小时步 Δt 的时间段内，可假定荷载（或应力）为常量，从而使问题简化为常量应力条件下的蠕变问题[17]。设变形体内任意一点在时刻t的一维应力状态为 σ(t)，对应时刻的蠕变应变为εc(t)，则蠕变应变-应力关系可表示为

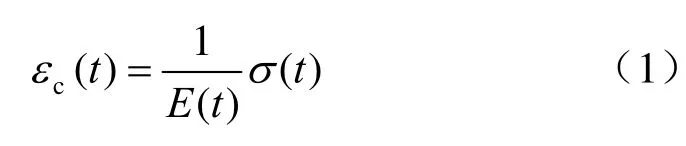
式中：E(t)为黏弹性模量，对于不同的流变模型可导出相应的黏弹性模量 E(t)。

推广至三维情况，则有

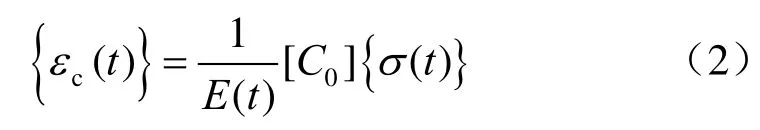
式中：[C0]为泊松比矩阵，对平面应变问题可以写为

考虑材料的蠕变，任意时刻的应变包括弹性应变和蠕变应变两部分，并表示为

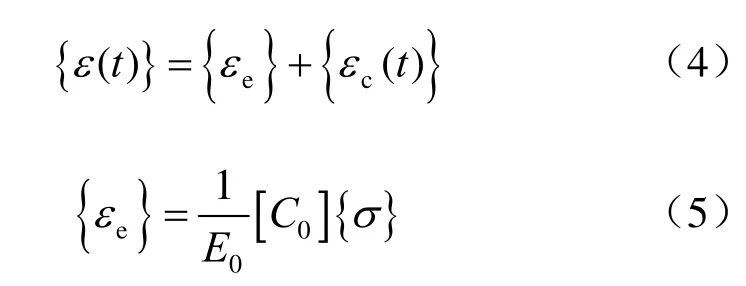
式中：｛εe｝为弹性应变列阵；｛σ(t)｝为t时刻的应力列阵；｛εc(t)｝为t时刻的蠕变应变列阵。

线弹性的应力-应变关系可以表示为

式中：［D0］为 E0=1时的弹性矩阵（E0为弹性模量）；［D0］=［C0］-1或［C0］=［D0］-1。

有限元分析中，通常把蠕变应变视为“弹性系统”的初应变，即令｛ε0｝=｛εc(t)｝。具有初应变的“弹性系统”应力-应变有如下关系：

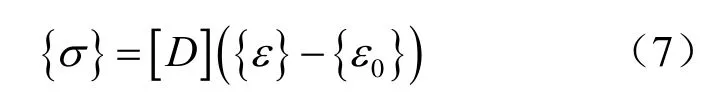
任一时刻t 的黏弹性应力-应变关系可写为

将式（2）代入式（8），则有

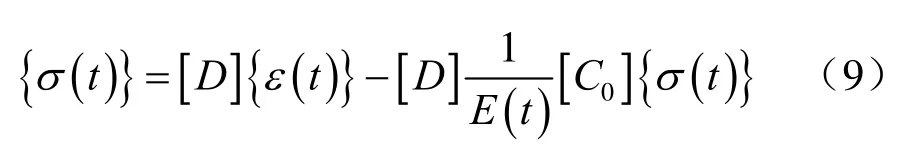
由于［D］=E0［D0］，且［D0］=［C0］-1，故有

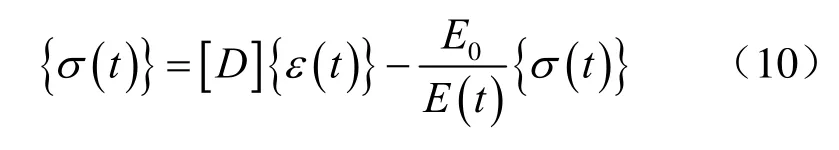
经移项合并后可得与线弹性问题具有相同形式的黏弹性问题本构关系：

流变效应不仅与当时的应力水平有关，而且取决于整个应力历史过程。为了分析黏性体的流变，应采用增量方法，以合适的时间步长逐步的进行计算。由流变试验可知，在应力水平较低的情况下，广义Kelvin 模型可以很好地模拟Ⅲ、Ⅳ级岩体的流变特性。

由广义Kelvin 模型，可得

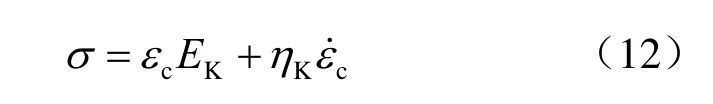
假定在很小的 Δt时间间隔内σ 保持不变，在t →t+Δt时段内积分可得

式中：εc（t+Δ t）为t+Δt时刻黏弹性蠕变应变量；εc（t）为时刻t 的黏弹性蠕变应变量。

若假定泊松比μ 不随时间变化，则可得黏弹性模型复杂应力状态下的应力-应变关系：

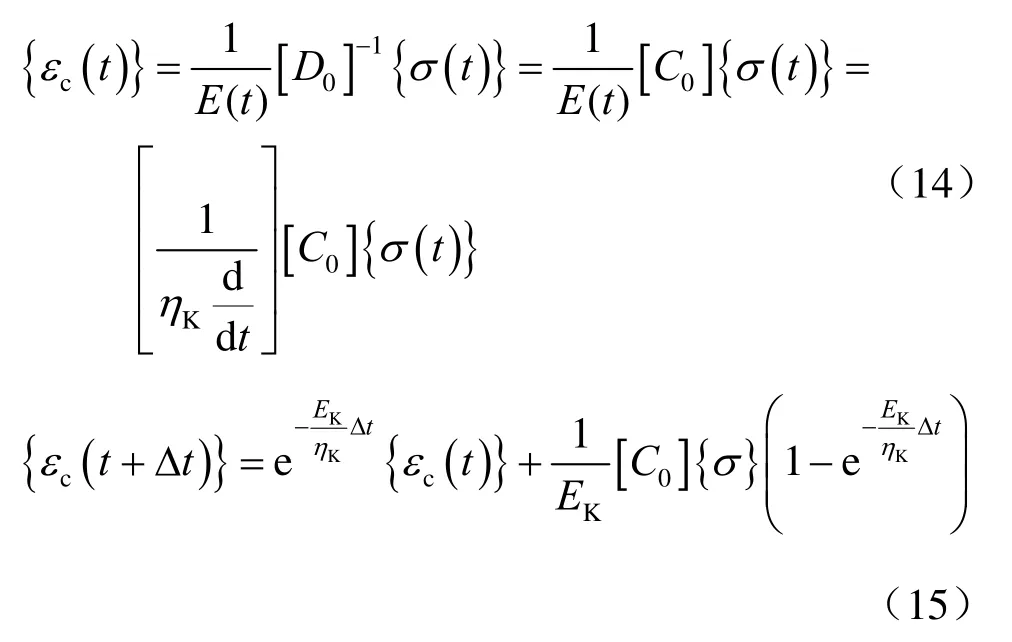
4 围岩参数反分析

选取江西武吉高速公路何市隧道作为计算对象（见表4），建立模拟分步开挖的有限元模型，利用某施工步监测到的位移进行优化反分析，以得到黏弹性本构模型难以确定的材料参数。

隧道断面支护方式和开挖方式参照隧道设计资料，Ⅲ级围岩典型断面如图6 所示。隧道净宽10.5 m，净高7.85 m。根据隧道开挖的影响范围，向上取隧道断面的自由边界，向下取30 m；模型向左右各取3 倍左右开挖范围，即50 m，计算模型图如7 所示。

表4 计算选取断面情况Table 4 Calculation selected sectional cases

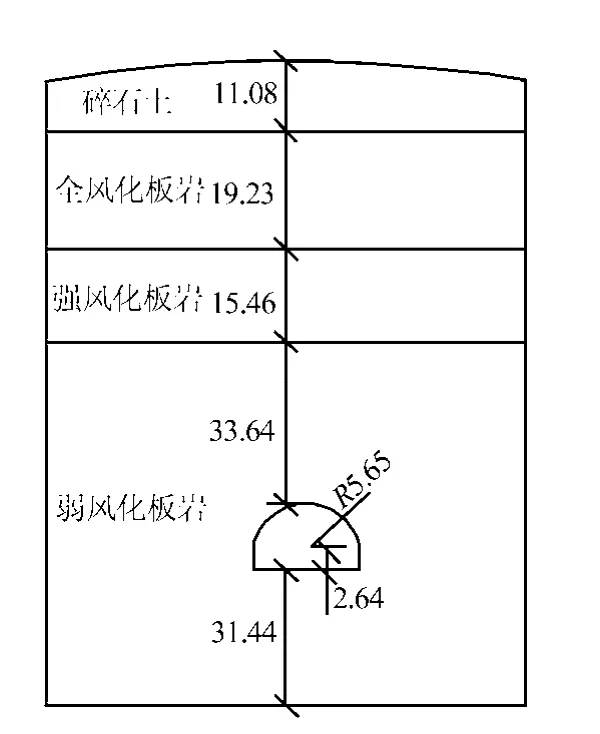
图6 Ⅲ级围岩典型断面(单位：m)Fig.6 Typical sections of Ⅲ grade rocks（unit:m）

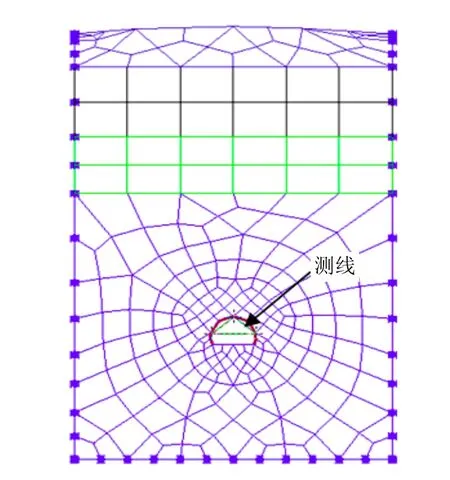
图7 Ⅲ级围岩计算模型Fig.7 Calculation model of Ⅲ grade rock

模型两侧约束水平向位移，模型底部约束y 向位移。衬砌支护参数见表5，岩体力学参数根据《公路隧道设计规范》[18]取值，见表6。

表5 隧道衬砌结构材料参数Table 5 Material parameters of the tunnel lining

表6 Ⅲ级围岩反分析力学参数Table 6 Mechanical parameters back analysis of Ⅲ grade rocks

利用施工监测到的收敛位移，通过已建立的有限元模型，根据黏弹性本构模型，进行优化反分析，以确定待反演的材料参数。

将广义Kelvin 模型中的E1、E2、η为待反演参数。图8为计算所得收敛值与实际检测值得对比分析图。从图中可知，计算值和实测值的大小基本一样，说明反演的正确性。Ⅲ、Ⅳ级围岩反演得到的参数见表7。

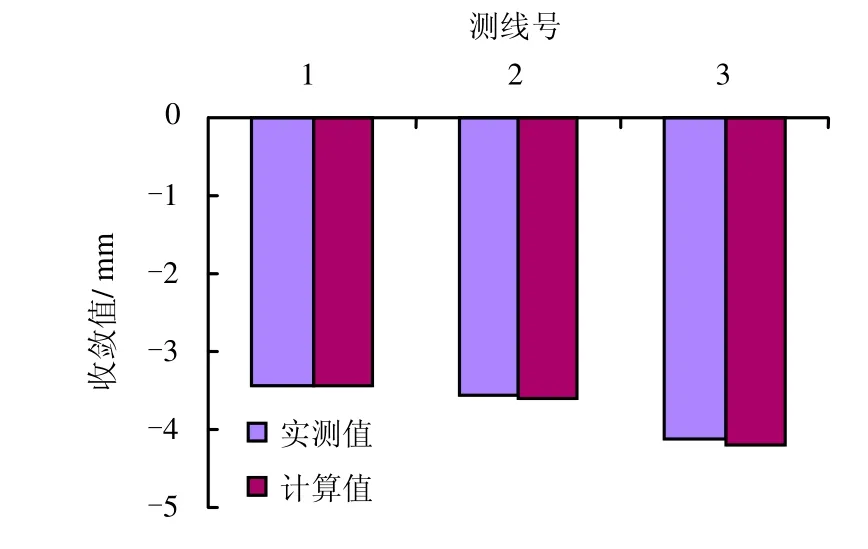
图8 计算值与实测值对比Fig.8 Comparison of calculated and measured values

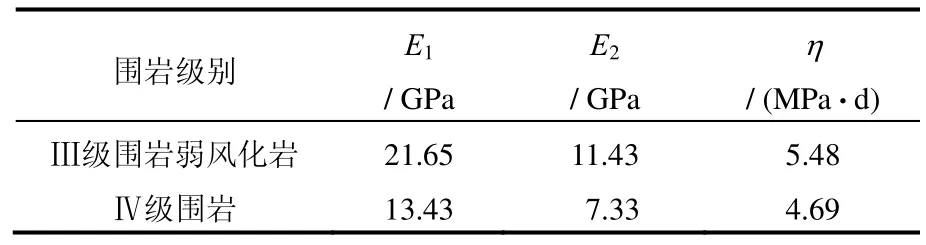
表7 Ⅲ、Ⅳ级围岩反演参数Table 7 The inversion parameters of Ⅲ and Ⅳgrade rocks

5 隧道围岩变形预测

利用章节4 反演得到围岩的黏弹性参数的均值对隧道YK83+250 断面进行有限元计算分析，并利用计算的位移与实际监测到的位移进行对比，以检验所提的反分析方法的可行性。参照表7 中的黏弹性参数，隧道断面的计算力学参数见表8。该隧道断面的施工过程与Ⅲ级围岩相似。有限元计算模型及剖分网格如图9 所示。通过黏弹性正分析对隧道开挖后不同时刻的围岩变形进行了预测，拱顶位移计算结果如图10 所示。由图可见，预测值与实测值基本吻合，变形趋势一致，变形稳定时间也基本一致，满足工程预测精度的需要。

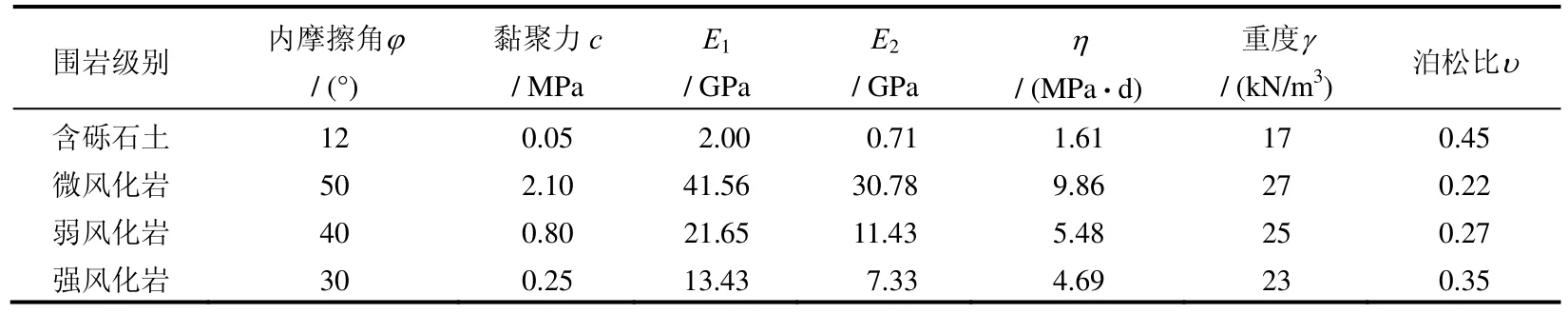
表8 断面YK83+250 围岩物理力学参数Table 8 Physico-mechanical parameters of YK83+250 rocks

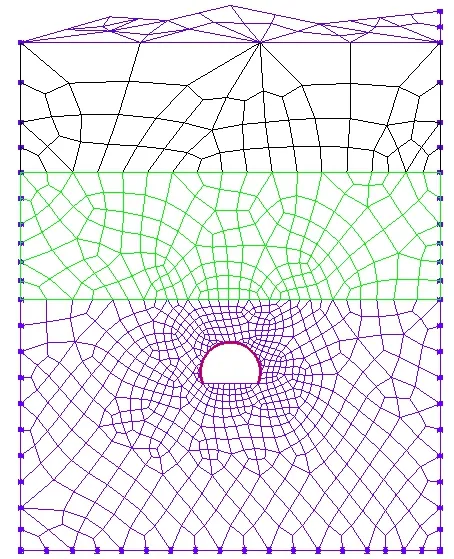
图9 断面YK83+250 有限元计算模型Fig.9 Finite element model of YK83+250

图10 YK83+250 断面拱顶下沉实测值和计算值Fig.10 Settlement measured and calculated values of YK83+250

综上，利用已有的施工监测数据反演围岩参数，再利用反演得到的围岩参数对下一时刻的围岩变形以及稳定时间进行合理的预测分析，这种基于施工过程的动态反分析方法是可行的。计算结果表明预测值和实际监测值误差满足施工应用需要，因此，动态反分析理论是实际指导施工中一种较为有效地方法。

6 结 语

通过对围岩流变特性的剪切试验研究以及模型辨识，得到了Ⅲ、Ⅳ级围岩分级加卸载单轴流变试验的全过程曲线。试验结果表明，围岩具有瞬弹性和黏弹性共存的特性，可用广义Kelvin 模型模拟。

结合剪切流变试验结论，推导了黏弹性模型复杂应力状态下的应力和应变关系公式。

基于所推导的本构关系，对江西高速公路隧道围岩参数进行反分析。结合反分析结果，对隧道围岩变形进行预测，预测值与实测值基本吻合，变形趋势一致，满足工程预测精度的需要。

[1]孙钧.岩土材料流变及其工程应用[M].北京:中国建筑工业出版社,1999.

[2]GRIGGS D.Creep of rocks[J].Journal of Geology,1939,47(8):225-251.

[3]WAWERSIK W R.Time 2 dependent behaviour of rock in compression[C]//Advances in Rock Mechanics Proc.3rd Congr.Int.Soc.Rock Mechanics.Colorado:[s.n.],1974:357-363.

[4]AMADEI B,CURRAN J H.Creep behaviour of rock joints[C]//13th Canadian Rock Mechanics Symposium.[S.l.]:[s.n.],1980:146-150.

[5]OKUBO S,NISHIMATSU Y,FUKUI K.Complete creep curves under uniaxial compression[J].Int.J.Rock Mech.Min.Sci.Geomech.Abstr.,1991,28(1):77-82.

[6]MARANINI E,BRIGNOLI M.Creep behaviour of a weak rock:experimental characterization[J].Int.J.Rock Mech.Min.Sci.,1999,36(1):127-138.

[7]徐平,夏熙伦.三峡工程花岗岩蠕变特性试验研究[J].岩土工程学报,1996,18(4):63-67.XU Ping,XIA Xi-lun.Experimental study on creep properties of granite in the Three Gorges Project[J].Chinese Journal of Geotechnical Engineering,1996,18(4):63-67.

[8]来结合,张忠亭,罗居剑,等.锦屏水电站绿片岩蠕变特性研究[C]//第八届全国岩石力学与工程学术大会论文集.北京:科学出版社,2004.LAI Jie-he,ZHANG Zhong-ting,LUO Ju-jian.Research greenschist creep characteristics of Jinping Hydropower Station[C]//Proceedings of the eighth national academic circles of Rock Mechanics and Engineering Conference.Beijing:Science Press,2004.

[9]郝哲,刘斌,万明复.硐室的围岩稳定性反分析[J].中国矿业,2003,12(4):56-59.HAO Zhe,LIU Bin.Backward analysis on stability of surrounding rock of cave[J].China Mining Magazine,2003,12(4):56-59.

[10]杜丽惠,黄丽清.考虑围岩蠕变特性的轴对称有限元非线性分析[J].水利学报,2001,46(1):85-89 .DU Li-hui,HUANG Li-qing.Analysis of rock creep characteristics considered axisymmetric nonlinear finite element[J].Journal of Hydraulic Engineering,2001,46(1):85-89 .

[11]KAVANAGH K T,CLOUHG R W.Finite element application in the characterization of elastic solids[J].International Journal of Solids and Structures,1971,7(1):11-23.

[12]KIRSTEN H A D.Determination of rock mass elastic moduli by back analysis of deformation measurement[C]//Proceedings of Symposium on Exploration for Rock Engineering.Johannesburg:[s.n.],1976:1154-1160.

[13]MAIER G,JURINA L,PODOLKA K.On model identification problems in rock mechanics[C]//Proceedings of the 3rd International Conference on Numerical Methods in Geomechanies.Capri:[s.n.],1977:257-261.

[14]杨志法,刘竹华.位移反分析在地下工程设计中的初步应用[J].地下工程,1981,11(2):20-24.YANG Zhi-fa,LIU Zhu-hua.Application of back analysis method of displacement to underground engineering design[J].Underground Engineering,1981,11(2):20-24.

[15]冯紫良,杨林德,李成江.初始地应力的反推原理[J].隧道工程,1983,20(4):42-48.FEN Zi-liang,YANG Lin-de,LI Cheng-jiang.The backstepping principle of initial ground stress[J].Tunnel Engineering,1983,20(4):42-48.

[16]徐平,杨挺青.岩石流变试验与本构模型辨识[J].岩石力学与工程学报,2001,20(增刊):1739-1744.XU Ping,YANG Ting-qing.Current research on the rheological test and model identification of rock[J].Chinese Journal of Rock Mechanics and Engineering,2001,20(Supp.):1739-1744.

[17]曹树刚,边金,李鹏.岩石蠕变本构关系及改进的西原正夫模型[J].岩石力学与工程学报,2002,21(5):632-634.CAO Shu-gang,BIAN Jin,LI Peng.Creep constitutive relationship of rocks and a Modified model[J].Chinese Journal of Rock Mechanics and Engineering,2002,21(5):632-634.

[18]重庆交通科研设计院.JTG D70-2004 公路隧道设计规范[S].北京:人民交通出版社,2004.