基于组合赋权的岩爆倾向性预测灰评估模型及应用

裴启涛 ，李海波，刘亚群，张国凯

（1.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，武汉 430071；2.长江科学院 水利部岩土力学与工程重点实验室，武汉 430010）

1 引 言

岩爆是深部高地应力区岩体开挖过程中常见的一种地质灾害，常常表现为片状剥落、严重片帮，有的伴有声响及岩片弹射、能量猛烈释放、洞室突然破坏，往往给人员、设备和建筑的安全带来巨大损失[1]。历史上最早的、有资料记载的岩爆发生于1738年英国的锡矿坑道，我国最早记录的煤爆发生于1933年抚顺胜利煤矿[2-3]。岩爆的形成机理较为复杂，且危害性极大，随着地下资源开采及地下空间开发利用的不断深入，岩爆问题也越来越突出。

大量工程实例表明，岩爆是一种非常复杂的动力失稳现象，其涉及到的影响因素众多，不仅包括岩体的结构、强度及力学性质等内因，还有开挖围岩引起的应力和能量的变化等外因。目前，国内外大部分学者倾向于采用多指标综合评价法来对岩爆灾害进行预测研究，比较有代表性的，如模糊数学综合评判法[1]、人工神经网络法[3-4]、专家系统法[5]、距离判别分析法[6]、支持向量机法[7-8]、AdaBoost组合学习法[9]、属性综合评价法[10]、物元可拓法[11]和未确知测度评价法[12]等。在这些指标体系的研究及评判方法中，一个突出的问题是如何合理地确定各评价指标的权重。目前赋权的方法有很多，如模糊评价法、专家调查法、层次分析法、功效系数法、熵权法、人工神经网络法及灰色关联度分析法等。这些方法在指标评价分析中发挥了积极的作用，但有些仍存在一定的不足，如专家调查法主观性较强，且实现比较困难；模糊数学综合评判法过度强调极值作用，容易丢失有效信息；熵权法仅仅依赖指标变异程度，在信息有限的情况下会产生偏差；人工神经网络法依赖于学习样本的容量，样本较少时评价精度往往不高。

由于岩爆是内、外多因素综合作用的结果，这些因素在岩爆的孕育过程中所起的作用有些比较明确，有些尚不完全清楚，即使是一些较为明确的因素，其具体量值也并非完全确定，而是属于某一区间内的灰数。因此，可以将岩爆与其影响因素间的关系当作一个灰色系统，采用灰色聚类理论进行研究。在这方面，姜彤等[13]基于灰色关联分析和模糊模式识别原理，建立了岩爆预测模型，并提出动态权重计算方法和综合评判指数的概念。谢学斌等[14]采用灰色白化权函数聚类方法，对国内外岩爆实例进行分析，发现该方法具有较高的预测准确率。然而，传统的岩爆预测灰评估模型存在多重交叉性及不满足规范性等缺陷，为此，笔者对其进行了改进[15]，取得了良好的效果。

为了较合理地确定岩爆灾害评价中各指标的权重，笔者提出了一种组合赋权方法，并将其与改进的灰评估模型相结合进行岩爆灾害预测。该模型通过对基本熵权法进行改进，解决了熵权法在某些情况下不适用的问题，然后引入欧几里得距离函数，使得主、客观权重之间和偏好系数间的差异程度一致，从而获得理想的综合权重。此外，通过对灰色聚类法进行优化，并依据岩爆综合聚类系数及判定准则进行岩爆灾害预测。利用该模型对国内外一些重大深部岩石工程岩爆案进行分析，进一步验证该模型的有效性及实用性，为岩爆的准确预测提供了一种切实可行的途径。

2 灰色聚类法原理及评价步骤

灰色聚类法属于灰评估理论，是灰色系统理论的重要组成部分，它依据不同聚类指标所拥有的白化数将聚类对象（或观测对象）按事先划分的灰类进行归纳，以判定该聚类对象所属的类别[16]。

设有n个岩爆聚类对象，m个聚类指标，s个不同的灰类，记xij为岩爆对象i(i=1,2,…,n)对于聚类指标 j(j=1,2,…, m)的样本；(·)为j指标k(k=1,2,…,s)灰类对应的白化权函数；为j指标k 灰类的权，则岩爆样本的矩阵X 满足：

鉴于端点白化权函数存在灰类多重交叉性及不满足规范性等缺陷，笔者对灰色聚类法进行优化[15]，构造适用于岩爆各指标的中心点白化权函数，并依据 xij的值将对象i 进行归类，主要步骤如下：

①根据岩爆所要划分的灰类数，分别确定k(k=1,2,…,s)灰类中心点 λk，并将指标j 的取值范围相应地划分为s个灰类。

②将灰类向不同方向进行延拓，并增加0 灰类和 s+1 灰类，并确定其转折点分别为λ0、λs+1。

⑤判断岩爆对象i 属于灰类 k*的关系式满足：

此外，当有多个对象同属于 k*灰类时，还可根据综合聚类系数大小确定各个对象的优劣。

3 利用组合赋权法确定综合权重

进行岩爆灾害预测分析时，各评价指标的权重较为重要，直接影响着预测结果的准确性及有效性。在现有的岩爆灾害评价模型中，常用的权重确定方法有主观赋权法和客观赋权法。实际操作时，主观赋权法，如专家经验法、模糊评价法等由于人的主观因素会对评价结果产生影响。同样，客观赋权法，如熵权法等可能会因各指标数据所提供的信息量而造成偏差。

为了既反映对岩爆孕育机理的直观认识，又兼顾客观调查数据的规律，笔者将专家经验法获得的主观权重χj与利用熵值法计算得到的客观权重ηj相结合，从而获得理想的综合权重wj，即

式中：α、β（≥0）分别为聚类指标的主、客观权重的偏好系数。

为了使主、客观赋权法得到的权重间的差异程度与其相对应的偏好系数间的差异程度相一致，引入欧几里得距离函数d(χj,ηj)，并令该距离函数与偏好系数存在以下关系：

确定客观权重时，笔者采用改进熵权法进行计算。在信息论中，熵值是系统无序化程度的一个度量，即从量上可以反映具有一定概率事件发生时所传递的信息，因此，可以利用熵权法评价所获系统信息的有序度及有效性，从而确定指标权重。

利用信息熵理论获得不同评价指标的熵值方法主要步骤[17-18]如下：

Step2：计算系统中第j个聚类指标的熵值Ej：

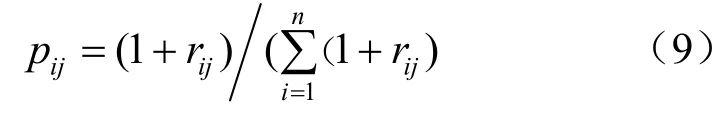
Step3：依据第j个指标的熵值，计算其熵权ηj：

值得注意的是，利用基本公式（10）进行熵权计算时主要存在以下2个问题：

（1）若指标熵值Ej→1(j=1,2,3,… ,m)时，其相互之间的微小差别可能引起不同指标熵权的较大变化，如熵值向量(0.999 9,0.999 8,0.999 7)计算熵权为(0.166 7,0.333 3,0.500 0)，显然不合理（见表1）。

（2）若1-Ej比例相同，无论熵值间差异程度如何，不同指标下熵权计算结果相同，如熵值向量(0.9,0.8,0.7)、(0.8,0.6,0.4)和(0.7,0.4,0.1)计算结果均为(0.166 7,0.333 3,0.500 0)，显然不合理（见表1）。因此，需要对基本公式进行改进。依据信息熵原理，本文提出的改进熵权计算公式，见式（11）。

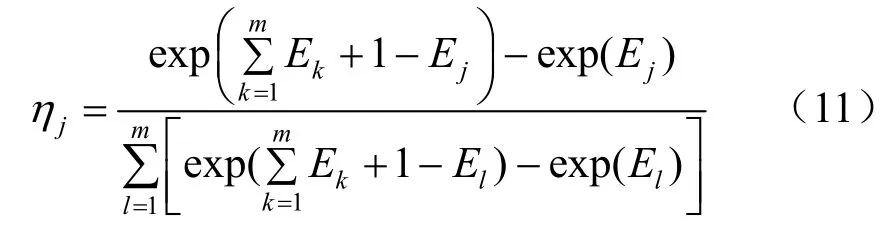
满足0≤ηj≤1，且。

证明：（1）假设一系列指标熵值Ej(j=1,2,3,…,m)的平均值为，即。令εj=，可知。若存在一正数ε，满足，当评价指标集中的各指标熵值仅发生微小变化时，满足关系：当ε→0时，有εj→0。根据极限法则，可得

由此可知，当评价指标的熵值Ej发生微小变化时，各指标熵权近似相等，该结果与实际情况相吻合，即不存在问题（1）的情况。

（2）由式（11）可知，熵权ηj并非取决于1-Ej的比例，而是与指数相关，因此不存在问题（2）的情况。

为了便于对比基本公式与改进公式的熵权计算效果，以3个指标为例分别计算熵值在不同情况下的熵权差别，见表1。通过对表1 分析可知，改进公式克服了基本公式存在的上述问题，理论上更完备，可以采用式（11）作为熵权的计算公式。

表1 不同熵权计算公式的计算结果比较Table 1 Comparison of entropy weight results by two computation formulas

4 基于组合赋权的岩爆倾向性预测灰评估模型（GEM-CW）

4.1 岩爆评价指标

岩爆的评价指标应涵盖岩爆发生的内、外因多因素下的综合条件，具有较好的代表性，此外，还应该易于获取（如通过室内试验或现场测试），并能够在不同的工程实例间进行相互比较。参考有关岩爆烈度评判指标体系研究[1,6,12,19-20]，根据岩爆的成因及特点，这里选最大切应力σθ、单轴抗压强度σc、单轴抗拉强度σt及岩石弹性能量指数 Wet作为影响岩爆的主要因素，以应力系数σθ/σc、脆性系数 σc/t及弹性能量指数Wet作为判定岩爆发生等级的评价指标。这些评价指标在模糊数学模型[1]、距离判别模型[6]、属性综合评价模型[10]、物元可拓模型[11]和未知测度模型[12]中均获得广泛的应用，取得了良好的效果。本文参照王元汉等[1]给出的岩爆烈度与上述3个指标之间的关系（见表2），对岩爆灾害进行预测。

结合章节2 可知，用于岩爆灾害预测的聚类指标数m=3，可能发生的岩爆灰类数s=4，各灰类对应的岩爆等级依次划分为无岩爆（k=1）、弱岩爆（k=2）、中等岩爆（k=3）及强烈岩爆（k=4）。

表2 岩爆烈度与评价指标间的关系Fig.2 Relationship between rockburst classification and evaluation indexes

4.2 构造灰类的中心点白化权函数

根据表2，构造适用于岩爆灾害预测的各灰类中心点白化权函数（见图1）。图1 中，λ1、λ2分别为灰类2 和灰类3 聚类指标分界线的中心点；0λ、λ3分别对应灰类1 和灰类4 的白化权函数转折点；a1～a3对应于表1 各聚类指标的3个分类界限值。由几何关系可知，λ0=2a1-λ1，λ3=2a3-λ2。

不同类型的白化权函数表达式为式（13）～（16），依据岩爆评价指标绘制的各类白化权函数形式见图2。

4.3 确定各指标的权重系数

根据章节3 的组合赋权法原理，确定 j(j=1,2,3)指标的综合权重系数wj。

4.4 确定综合聚类系数σik及岩爆灾害的预测

由于岩爆聚类指标的意义、量纲不同且在数量上悬殊较大，为了避免某些指标参与聚类的作用减小，本文采用灰色定权聚类进行计算，即有=wj。然后，依据式（2）、（3）进行计算，即可对岩爆灾害进行较合理地分类。

4.5 具体实现过程

首先，通过现场资料收集和室内岩石力学试验，获得各评价指标量值。然后，通过计算机编程，利用组合赋权的灰评估模型进行岩爆灾害预测。具体实现过程如图3 所示。

图1 不同类型的中心点白化权函数示意图Fig.1 Sketch of different enter-point whitenization weight function

图2 不同岩爆评价指标下的中心点白化权函数Fig.2 Enter-point whitenization weight function of different rockburst evaluation indexes

图3 组合赋权灰评估模型计算流程图Fig.3 Calculation flow chart of GEM-CW

5 工程应用

为了检验基于组合赋权的灰评估模型在岩爆预测中的有效性及实用性，以王元汉等[1]统计的国内外若干大型岩石地下工程岩爆案例进行分析，见表3。

首先，依据式（8）、（9）及式（11）计算岩爆案例评价指标的熵值向量 E=(0.9972 0.902 3 0.955 2)T，熵权向量=η(0.313 2 0.355 3 0.331 5)T，并利用欧几里得距离函数确定主、客观权重的偏好系数α=0.553 8，β=0.446 2，则岩爆各聚类指标的综合权重向量w=(0.361 3 0.324 7 0.314 0)T。其次，根据式（13）～（16）计算岩爆案例x 所属k灰类的隶属度(x)。最后，依据综合聚类系数表达式（2）及岩爆烈度评价关系式（3）来判别岩爆的类别。将岩爆综合聚类系数及评价结果列入表4，同时统计了利用模糊综合评价法、属性综合评价法、物元分析法及未确知测度法的评价结果。

表3 国内外一些典型的工程岩爆分析初始数据资料Table 3 Initial data for rockburst analysis of some typical projects in domestic and abroad

表4 灰评估模型预测结果对比Table 4 Comparison of prediction results obtained with different methods of grey evaluation model

由表4 可知，除了样本5、9、13 和18 的预测结果与实际情况存在一定的偏差之外，其余的岩爆样本灰评估的评价结果与实际情况相吻合。

由此可见，采用灰评估模型进行岩爆发生与否及烈度等级的预测是完全可行的和高效的，具有较高的工程应用价值。

6 结 论

（1）针对岩爆灾害评价中各指标权重难以确定的问题，提出了一种组合赋权方法。通过对基本熵权法进行改进，理论上解决了熵权法在某些情况下不适用的问题，然后将改进的熵权计算值和主观赋权值相结合，并引入欧几里得距离函数，使得主、客观权重之间和偏好系数间的差异程度一致，较合理地获得岩爆分析中各指标的综合权重。

（2）鉴于岩爆灾害的发生与否及烈度等级预测受岩体内、外因等多种因素的影响，通过选取 σθ/σc、σc/σt及 Wet作为岩爆评价指标，并对灰色聚类法进行优化，同时结合组合赋权方法，建立了基于组合赋权的岩爆倾向性预测灰评估模型。利用建立的模型对国内外一些岩石工程岩爆实例进行分析，发现该模型的预测结果与实际情况吻合较好，且编程简单、方便，从而验证了该模型的有效性及实用性，为岩爆的准确预测提供一种切实可行的途径。

基于灰评估理论及组合赋权法建立的岩爆倾向性预测模型，其预测的精度及可靠性取决于岩爆主要影响因素的选取、白化权函数的构建方法和评价指标权重的确定，若能较合理地解决这些问题势必会进一步提高岩爆的预测精度。因此，本文建立的岩爆预测灰评估模型只是初步尝试，有些问题仍有待进一步研究。

[1]王元汉,李卧东,李启光,等.岩爆预测的模糊数学综合评判方法[J].岩石力学与工程学报,1998,17(5):493-501.WANG Yuan-han,LI Wo-dong,LI Qi-guang,et al.Method of fuzzy comprehensive evaluations for rockburst prediction[J].Chinese Journal of Rock Mechanics and Engineering,1998,17(5):493-501.

[2]古德生,李夕兵.现代金属矿床开采科学技术[M]. 北京:冶金工业出版社,2006.

[3]陈海军,郦能惠,聂德新,等.岩爆预测的人工神经网络模型[J].岩土工程学报,2002,24(2):229-232.CHEN Hai-jun,LI Neng-hui,NIE De-xin,et al.A model for prediction of rockburst by artificial neural network[J].Chinese Journal of Geotechnical Engineering,2002,24(2):229-232.

[4]FENG X T,WEBBER S,OZBAY M U,et al.Neural network assessment of rockburst risks for deep gold mines in South Africa[J].Trans.Nonferrous Met.Soc.China,1998,8(2):335-341

[5]FENG X T,WEBBER S,OZBAY M U,et al.An expert system on assessing rockburst risks for South African deep gold mines[J].Journal of Coal Science and Engineering(China),1996,2(2):23-32.

[6]宫凤强,李夕兵.岩爆发生和烈度分级预测的距离判别方法及应用[J].岩石力学与工程学报,2007,26(5):1012-1018.GONG Feng-qiang,LI Xi-bing.A distance discriminant analysis method for prediction of possibility and classification of rockburst and its application[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(5):1012-1018.

[7]赵洪波.岩爆分类的支持向量机方法[J].岩土力学,2005,26(4):642-644.ZHAO Hong-bo.Classification of rockburst using support vector machine[J].Rock and Soil Mechanics,2005,26(4):642-644.

[8]祝云华,刘新荣,周军平.基于v-SVR 算法的岩爆预测分析[J].煤炭学报,2008,33(3):277-281.ZHU Yun-hua,LIU Xin-rong,ZHOU Jun-ping.Rock burst prediction analysis based on v-SVR algorithm[J].Journal of China Coal Society,2008,33(3):277-281.

[9]葛启发,冯夏庭.基于AdaBoost 组合学习方法的岩爆分类预测研究[J].岩土力学,2008,29(4):943-948.GE Qi-fa,FENG Xia-ting.Classification and prediction of rockburst using AdaBoost combination learning method[J].Rock and Soil Mechanics,2008,29(4):943-948.

[10]文畅平.属性综合评价系统在岩爆发生和烈度分级中的应用[J].工程力学,2008,25(6):153-158.WEN Chang-ping.Application of attribute synthetic evaluation system in prediction of possibility and classification of rockburst[J].Engineering Mechanics,2008,25(6):153-158.

[11]熊孝波,桂国庆,许建聪,等.可拓工程方法在地下工程岩爆预测中的应用[J].解放军理工大学学报(自然科学版),2007,8(6):695-701.XIONG Xiao-bo,GUI Guo-qing,XU Jian-cong,et al.Application of extension method to prediction of rockburst of underground engineering[J].Journal of PLA University of Science and Technology(Natural Science),2007,8(6):695-701.

[12]史秀志,周健,董蕾,等.未确知测度模型在岩爆烈度分级预测中的应用[J].岩石力学与工程学报,2010,29(增刊1):2720-2726.SHI Xiu-zhi,ZHOU Jian,DONG Lei,et al.Application of unascertained measurement model to prediction of classification of rockburst intensity[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(Supp.1):2720-2726.

[13]姜彤,黄志全,赵彦彦.动态权重灰色归类模型在南水北调西线工程岩爆风险评估中的应用[J].岩石力学与工程学报,2004,23(7):1104-1108.JIANG Tong,HUANG Zhi-quan,ZHAO Yan-yan.Dynamically weighted grey optimization model for rockburst risk forecasting and its application to western route of south-to-north water transfer project[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(7):1104-1108.

[14]谢学斌,潘长良.岩爆灾害的灰类白化权函数聚类预测方法[J].湖南大学学报(自然科学版),2007,34(8):16-20.XIE Xue-bin,PAN Chang-liang.Rockburst predict ion method based on grey whitenization weight function cluster theory[J].Journal of Hunan University(Natural Sciences),2007,34(8):16-20.

[15]裴启涛,李海波,刘亚群,等.基于改进的灰评估模型在岩爆中的预测研究[J].岩石力学与工程学报,2013,32(10):2088-2093.PEI Qi-tao,LI Hai-bo,LIU Ya-qun,et al.Rockburst prediction based on a modified grey evaluation model[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(10):2088-2093.

[16]刘思峰,党耀国,方志耕,等.灰色系统理论及其应用(5 版)[M].北京:科学出版社,2010.

[17]周惠成,张改红,王国利.基于熵权的水库防洪调度多目标决策方法及应用[J].水利学报,2007,38(1):100-106.ZHOU Hui-cheng,ZHANG Gai-hong,WANG Guo-li.Multi-objective decision making approach based on entropy weights for reservoir flood control operation[J].Journal of Hydraulic Engineering,2007,38(1):100-106.

[18]梁桂兰,徐卫亚,谈小龙.基于熵权的可拓理论在岩体质量评价中的应用[J].岩土力学,2010,31(2):535-540.LIANG Gui-lan,XU Wei-ya,TAN Xiao-long.Application of extension theory based on entropy weight to rock quality evaluation[J].Rock and Soil Mechanics,2010,31(2):535-540.

[19]徐林生,王兰生,李永林.岩爆形成机制与判据研究[J].岩土力学,2002,23(3):300-303.XU Lin-sheng,WANG Lan-sheng,LI Yong-lin.Study on mechanism and judgement of rock bursts[J].Rock and Soil Mechanics,2002,23(3):300-303.

[20]张镜剑,傅冰骏.岩爆及其判据和防治[J].岩石力学与工程学报,2008,27(10):2034-2042.ZHANG Jing-jian,FU Bing-jun.Rock burst and its criteria and control[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(10):2034-2042.