宽斜齿轮多目标修形优化设计
蒋进科,方宗德,苏进展
(西北工业大学机电学院,710072,西安)
高速重载宽斜齿圆柱齿轮广泛应用于船舰等大功率传动系统中,其特点是同时啮合的齿对数多,易发生偏载现象,因此对其抗承载能力、抗胶合能力、低振动、低噪声等诸多方面有严格要求,单一目标的修形设计已经不能满足高性能齿轮传动装置的要求。文献[1-4]介绍了齿廓修形在抗胶合能力和减小振动、噪声方面的优点,文献[5]介绍了齿向修形在提高承载能力、改善齿面载荷分布方面的优点,文献[6]介绍了三维修形在均化齿面载荷和改善齿轮动态性能方面的显著作用。以上研究均未能提供修形状态下精确的齿面几何状况,或忽略了修形齿轮局部摩擦系数的改变对胶合计算影响及接触齿对对齿间载荷分布的影响,或未考虑轮齿动态性能,而且大多针对单一目标修形,因此这种设计的结果只能反映在假定条件下的最优设计方案。齿轮接触分析(TCA)[7-8]、承载接触分析(LTCA)[9]及弹流润滑剂(EHL)[10]理论的发展,为齿轮修形技术的深入分析与研究提供了重要工具。
本文将小轮法向修形曲面与理论齿面叠加,构造修形齿面,通过TCA、LTCA技术,得到齿面离散点载荷分布和承载变形,应用EHL理论确定接触线上各离散点的局部摩擦系数,建立斜齿轮啮合型弯-扭-轴-摆动力学模型,以齿面闪温、载荷密度、承载传动误差、啮合线方向相对扭转加速度均方根最小进行多目标优化,设计了最佳修形齿面。
1 修形齿面的构造
1.1 修形曲面设计
高精度宽齿轮通常进行齿端修薄,因此本文设计如图1所示的2段抛物线与1段直线表示的修形曲线,通过改变参数可以表示为齿端修薄与齿向修鼓曲线。为了便于测量和确定修形曲面,修形曲线通常用旋转投影面参数(x,y)表示
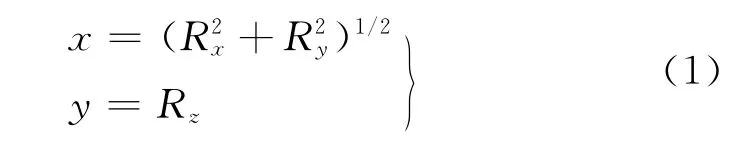
式中:Rx、Ry、Rz为理论齿面位矢坐标分量。
在旋转投影面上,将齿面分别沿齿高、齿长方向均匀划分为m×n个网格点阵,基于法向修形曲面计算网格节点上的修形量δ′(x,y),通过3次B样条对齿面网格节点数据拟合得到光滑的修形曲面δ(x,y)。宽斜齿易受轴扭转变形影响,引起齿面偏载,因此应进行螺旋角修形即齿向线性修形,齿廓采用4次抛物线修形主要为了降低闪温分布与振动。
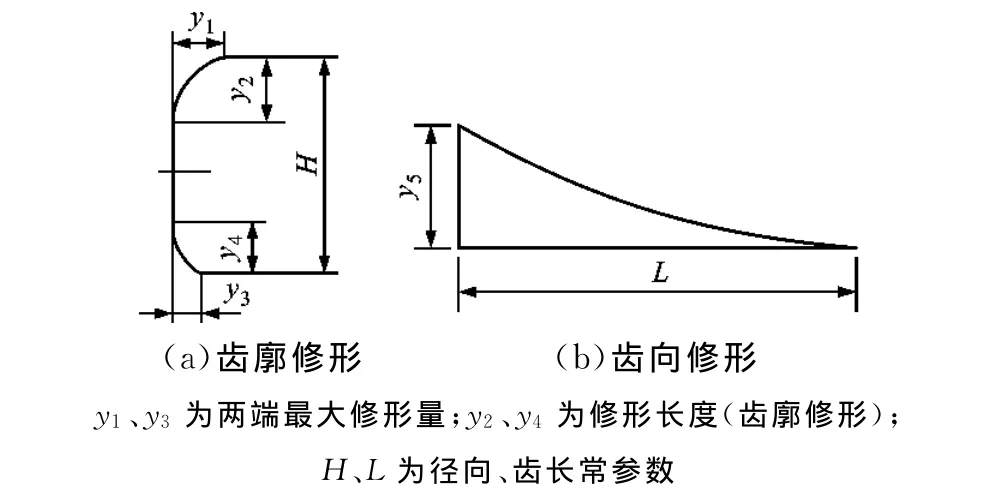
图1 齿廓、齿向修形曲线
1.2 修形齿面表达
通过理论齿面与法向修形曲面叠加,构造修形齿面,其位矢和法矢表示如下
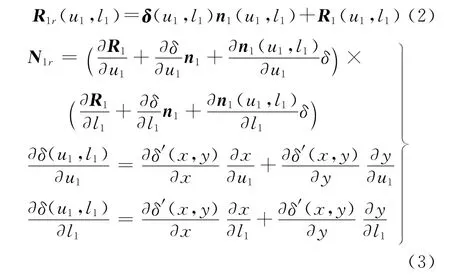
式中:R1、n1分别为小轮理论齿面位矢、法矢;R1r、n1r分别为小轮修形齿面位矢、法矢;δ为修形量;u1、l1为理论齿面参数。
2 优化模型
2.1 扭转变形计算
轴扭转变形引起宽斜齿齿面载荷不均匀,本文采用的LTCA是一种基于齿面柔度矩阵的规划方法[11],齿面在接触载荷下的变形特性被容纳于柔度矩阵中。由于被动轮直径大,截面抗扭模量大,且采用腹板结构较多,扭转变形影响很小,因此可只考虑小齿轮扭转的附加柔度。小轮齿面划分的网格如图2a所示,其旋转投影面上的节点标记如图2b所示,径向网格点(i=1,…,I),轴向网格点(j=1,…,J)。利用一维有限元方法计算轴扭转变形,小轮轴沿轴向分为与齿面轴向网格对应的J段如图2c所示,从右端输入扭矩,设在齿面点i施加单位法向载荷时,点j相对右端面的扭转角为φij,计算轴扭转变形产生的附加柔度系数,并与齿面网格法向柔度矩阵叠加,得到齿轮系统的齿面法向柔度矩阵
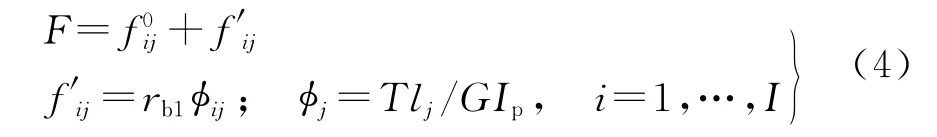
式中:rb1为小轮基圆半径;GIp为圆轴抗扭刚度;T为负载扭矩;lj为j节点处距端面距离。轴的扭转角仅与轴向节点j位置有关系,与径向节点i位置无关,因此需要将一维节点扭转角数据转换为与齿面节点维数相同,即φij(i=1,…,I)=φj。
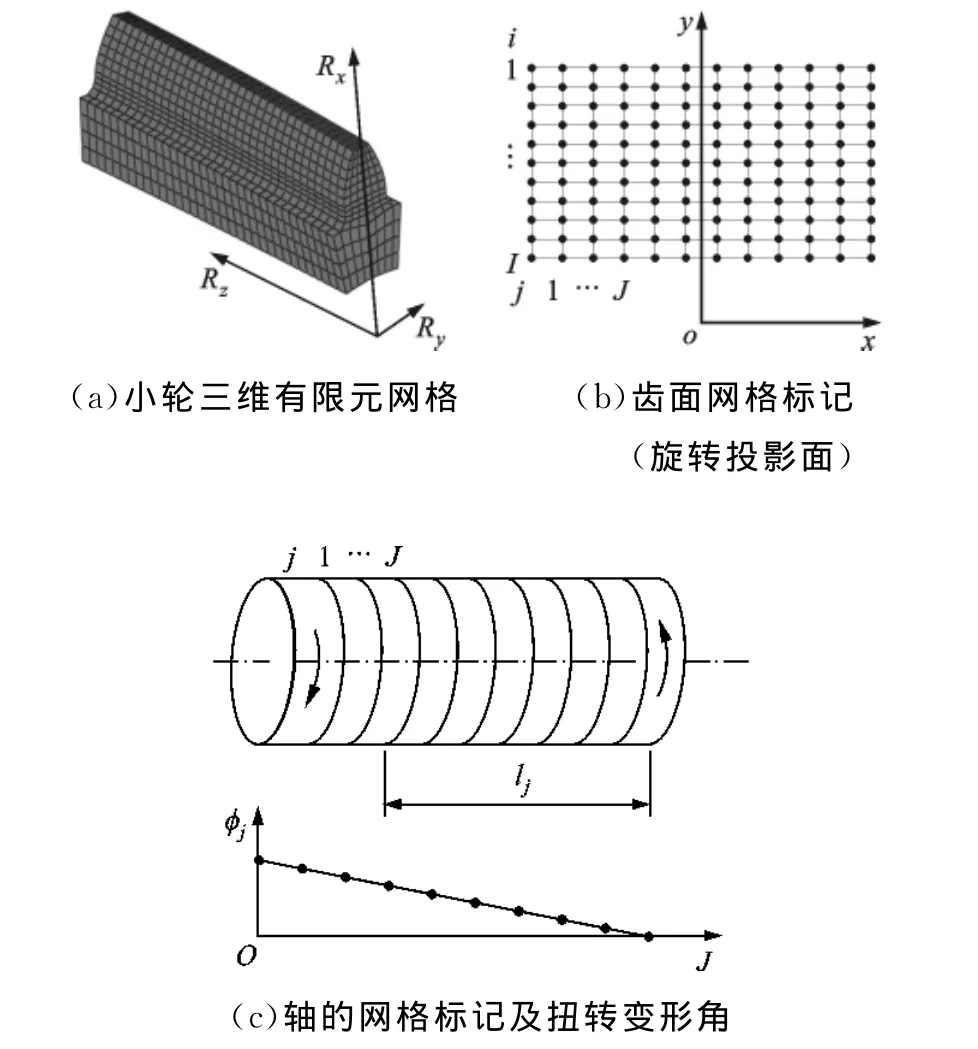
图2 齿面网格及轴的扭转变形角
2.2 多目标优化
首先通过TCA、LTCA计算,得到接触线上离散点的载荷分布pij及一个啮合周期轮齿法向位移Z,然后按以下过程进行优化。
(1)将Z转化为啮合线上位移,用转角表示承载传动误差(LTE)为
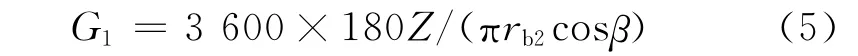
式中:rb2、β分别为被动大轮基圆半径和螺旋角。
(2)接触线上离散点载荷密度
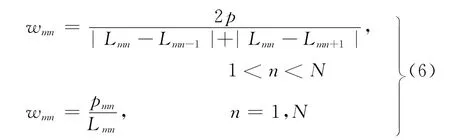
式中:Lmn为第m条接触线上第n个点位置,可通过TCA得到;N为接触线上离散点个数;M为接触线条数。
为表示载荷均匀程度,通常可用接触线上载荷密度的均方根最小或最大载荷密度最小表述,本文采用后者,最大载荷密度为
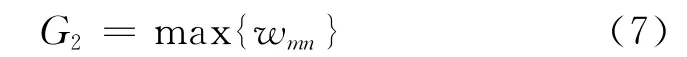
(3)根据渐开线圆柱齿轮胶合承载能力的Blok闪温公式,接触线上最大闪温积分为
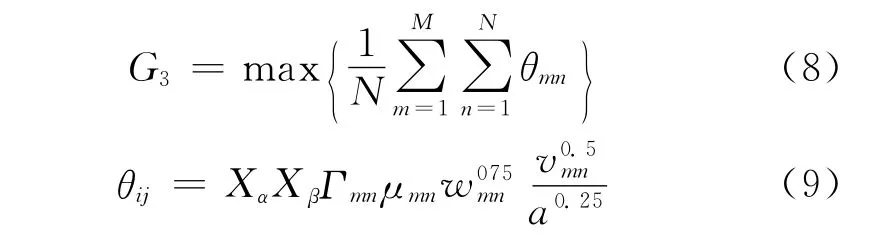
式中:μmn为啮合点的局部平均摩擦系数;Xα、Xβ为啮合角、螺旋角系数,均为常数1.0;vmn为啮合点线速度;a为啮合中心距;Γmn为啮合点几何参数,可通过TCA求解。
齿面摩擦系数可按如下公式计算[12]
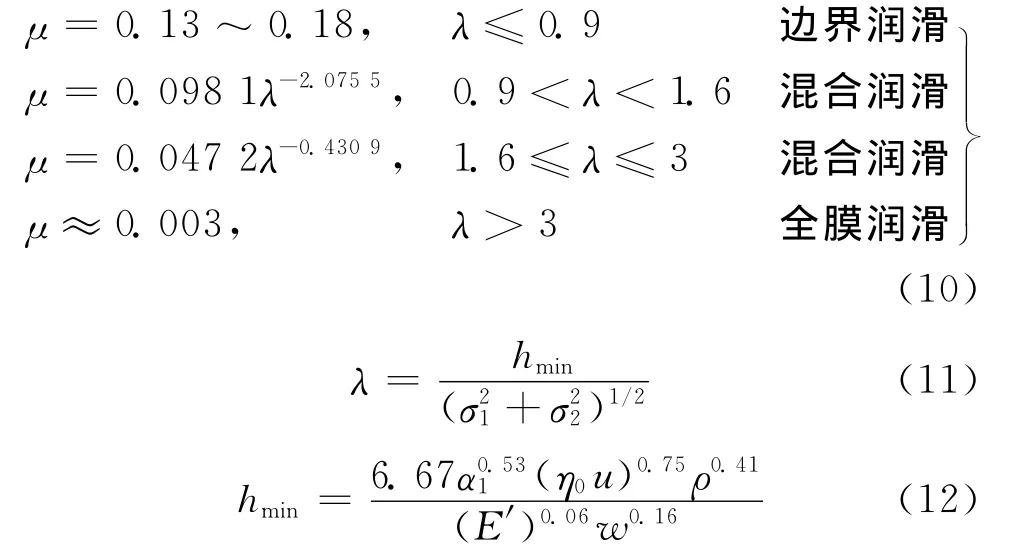
式中:λ为油膜比厚;hmin为最小油膜厚度[13];σ1、σ2为两接触表面轮廓的均方根偏差;ρ为综合曲率半径;α1为润滑油压黏系数;η为润滑油环境黏度;E′为当量弹性模量。
(4)根据一个啮合周期的承载变形Z确定时变啮合刚度,通过TCA、LTCA可确定啮入冲击力,将其展开为傅里叶级数。建立考虑时变刚度与啮入冲击激励的斜齿轮系统弯-扭-轴-摆10自由度动力学模型,其广义位移可表示为{xp,yp,zp,θpy,θpz,xg,yg,zg,θgy,θgz},动力学方程为[14]
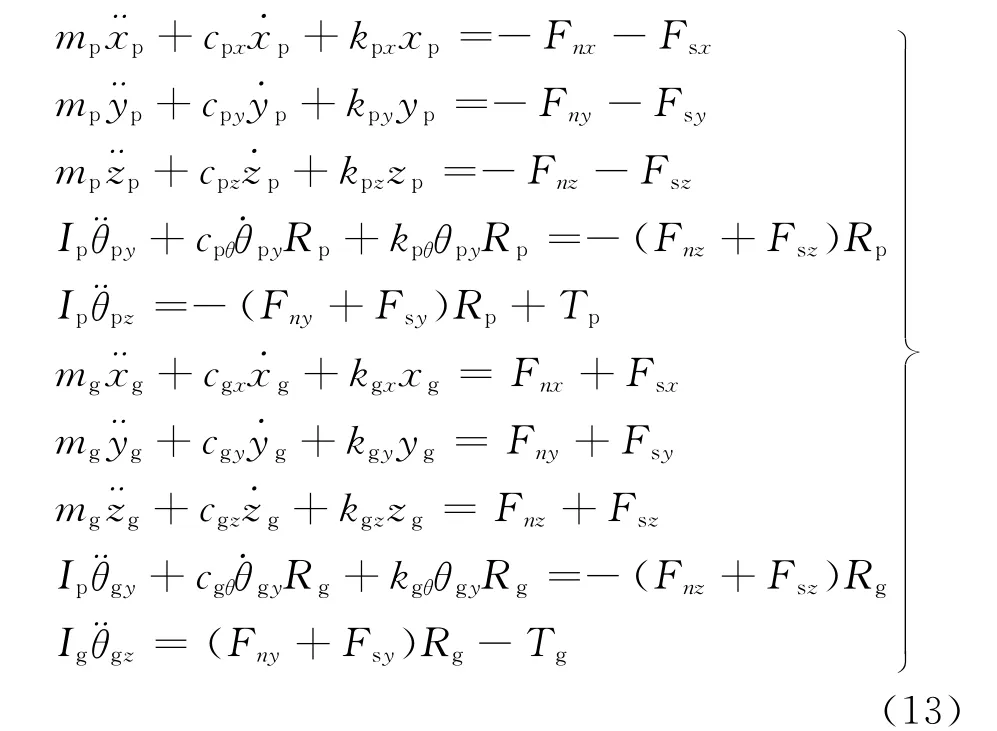
式中:xk、yk、zk(k为p,g)为主、被动齿轮中心点在横向、切向、轴向3个方向的平移振动位移;θky为主、被动齿轮中心点通过该中心并平行于y轴轴线的扭摆振动位移;θkz为主、被动齿轮绕传动轴轴线的扭转振动位移;Fnx、Fny、Fnz为法向啮合力Fn在x、y、z3个方向的分量;Fsx、Fsy、Fsz为啮入冲击力Fs在x、y、z3个方向的分量。根据冲击力学理论,冲击动能、最大变形δs与冲击力之间有如下关系[15]
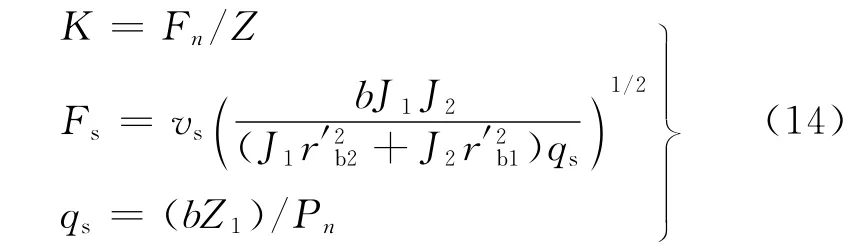
式中:J1、J2为小轮、大轮转动惯量;r′b1、r′b2为小轮、大轮瞬时基圆半径;b为齿宽;Fn为法向啮合力;Z1为啮入点法向承载变形量;Pn为法向静态啮合力。qs为啮入点轮齿综合柔度;vs为啮入冲击速度,可根据TCA确定啮入点位置,通过几何计算得到。
沿啮合线方向相对加速度均方根值可基本表示齿轮的振动和噪声的大小,其计算式为
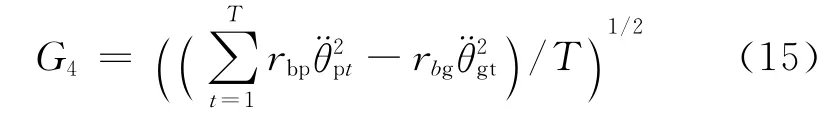
式中:G4(t=1,…,T)为一个啮合周期分为T 等份,第t时刻沿啮合线方向的相对振动加速度。因此,目标函数表示为
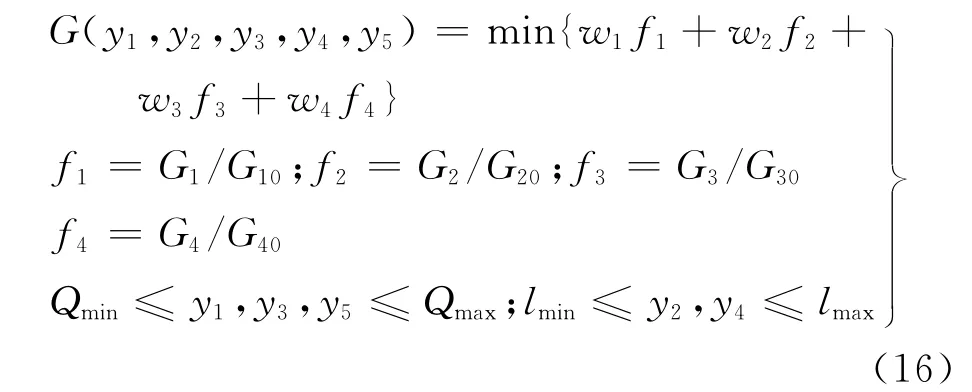
式中:y1~y5为优化变量,见图1;lmax、lmin、Qmax、Qmin分别为修形参数约束量;G10、G20、G30、G40为未修形的承载传动误差幅值、最大载荷密度、接触线上平均闪温、啮合线上相对扭转加速度均方根;w1、w2、w3、w4为目标权系数,文中权系数取相等值。
本文采用LTCA所求的啮合刚度已经考虑了安装及齿形齿距误差,即将误差激励合成在了刚度激励中,通过量纲统一化,利用变步长四阶Runge-Kutta数值积分方法对其求解。
2.3 优化过程及算法
优化过程即通过改变齿面接触状况,不断地求解TCA、LTCA及动力学方程的一个非线性迭代过程[16]。动力学求解较为耗时,因此需要寻找一种高效的优化方法,粒子群(PSO)算法具有全局收敛性,可以求解具有多个局部极值的非线性优化问题,缺点是该算法在进化后期,种群多样性消失,容易出现早熟停滞,从而陷入局部最优,为此作者对文献[17]中二阶振荡粒子群算法进行如下改进:①采用最大速度线性递减的方法平衡全局寻优能力与算法收敛精度的矛盾;②用指数自适应惯性权重平衡算法的全局和局部搜索能力;③迭代初期使用较大的加速因子c1和较小的c2,从而粒子可以较自由地在搜素空间中寻优,增加群内粒子的多样性,随着迭代次数的增加,线性递减c1,线性递增c2,加强了粒子收敛到全局最优解的能力。
学习因子二阶振荡使种群在粒子数目不变的情况下维持多样性,是提高全局搜索能力的主要方法,具体算法鉴于篇幅不做介绍。通过Rastrigin函数测试,结果如图3所示,表明该方法显著提高了PSO算法的寻优性能。
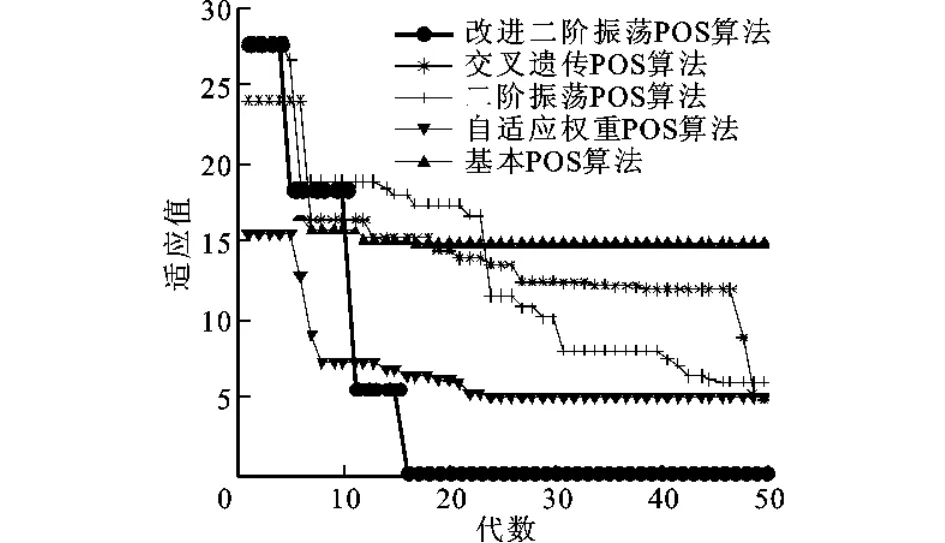
图3 智能优化算法测试结果
3 算例与分析
以标准安装齿轮副为例,其法向模数为6mm,小轮齿数为19,大轮齿数为47,法向压力角为20°,螺旋角为13°,齿宽为180mm,支撑刚度为5×109N·m-1,支撑阻尼为3.4×103N·m·s-1,进行大轮额定载荷2 000N·m、小轮额定转速2 000 r/min工况下的优化,优化的修形曲线参数结果:齿顶、齿根修形量(y1,y3)分别为17μm、20μm,修形长度(y2,y4)分别为3mm、2.5mm,沿齿向方向的线性修形中,动力输入端有较大修形量(y5),为8mm;优化后的承载传动误差幅值(G1)、最大载荷密度(G2)、最大闪温(G3)及啮合线方向相对扭转振动(G4)分别降低了53%、11%、61%、60%。图4为无修形、修形齿轮副的性能分析。
(1)齿面载荷、闪温分析。修形前载荷偏向动力输入端,修形量应从输入端至输出端递减。齿向的直线修形不改变齿面的几何接触印迹,使得几何传动误差从输入端至输出端减小,消除了扭转变形影响,重合度增加,因此修形后的载荷密度降低,沿齿向均匀分布,且齿间载荷分配曲线及载荷密度对称分布(见图4a、图4c、图4i)。啮入端综合曲率半径较小,无修形时,摩擦系数较大,齿向修形后载荷均匀;齿廓修形后,齿顶、齿根载荷降低,接触线上间隙增加,因此油膜厚度增加,润滑改善,摩擦系数明显降低(见图4e)。因此,齿顶、齿根闪温明显降低,且齿向的闪温分布趋于均匀,节圆附近由于相对滑动较小,闪温较小(见图4b、图4d)。由于齿廓、齿向的修形使得啮入、啮入端有较大的几何传动误差,因此啮入、啮出端载荷降低(见图4i)。修形后重合度增加,所以多载荷的传动误差(承载变形)幅值降低(见图4h),啮合刚度及幅值降低(见图4f、图4g)。
(2)啮入冲击分析。由于啮入端接触线上的载荷及轮齿啮合刚度降低,所以修形后啮合冲击降低(见图4l)。随转速增加冲击动能增大,则冲击力增大(见图4j)。由于啮合基节误差随外载荷增加而增大,同时无修形时啮合刚度的增大削弱了啮合齿对对冲击能量的缓冲能力,因此线外啮合冲击力大幅度增加;修形使得啮入点载荷、刚度及幅值降低,所以增强了齿对对冲击能量的缓冲能力,冲击力下降(见图4k)。
(3)系统振动分析。由于啮合冲击降低、啮合刚度幅值降低,因此修形后系统加速度降低,齿轮副啮合线上相对扭转振动和切向平移振动加速度要远大于齿轮轴向、横向、扭摆振动加速度(见图4m~图4q)。①当仅考虑刚度激励时,未修形时5 800r/min处为系统主共振,在2、1/3、1/2、2/3倍频处扭转、切向振动出现次共振,在2、1/3、1/2倍频处横向、轴向、扭摆振动出现次共振(见图4n);修形后由于啮合刚度降低,因此主共振转速下降到5 500r/min,在2、1/3、1/2倍频附近各方向振动明显降低(见图4m)。②在综合激励下,由于啮合冲击明显降低,修形后振动整体明显降低,随着转速增加,啮合冲击逐渐增加,使得啮合冲击激励远大于刚度激励的振动,因此共振敏感性降低(见图4o、图4p)。③在综合激励下,当载荷小于500N·m时,系统重合度较低,载荷的增加使得重合度增加,刚度波动降低,因此振动减小。当载荷大于500N·m时,系统重合度接近设计重合度,载荷增加使得斜齿轮啮合刚度、刚度波动增加,因此系统的振动随载荷增加逐渐增大;修形后主要是啮合冲击降低,因此较修形前振动明显降低(见图4q)。
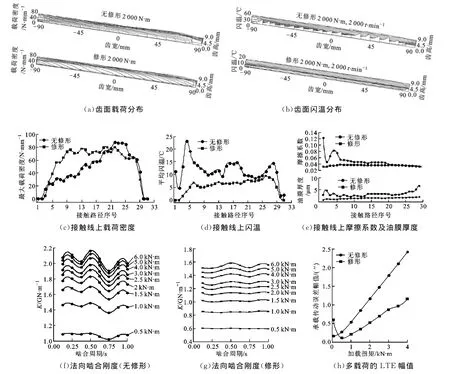
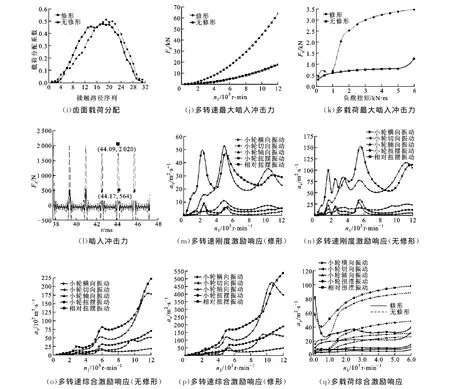
图4 宽斜齿轮多目标优化结果
4 结 论
(1)本文设计了宽斜齿修形齿面,计算了扭转变形产生的附加柔度矩阵,结合TCA、LTCA、EHL技术,确定了齿面接触位置几何参数、传动误差幅值、齿面载荷及闪温;通过LTCA计算得到轮齿时变啮合刚度及单对轮齿啮合刚度,根据啮合冲击模型,计算得到线外啮合冲击激励;应用集中参数法建立斜齿轮弯-扭-轴-摆耦合的动力学模型,采用变步长的四阶Runge-Kutta法进行求解,从而得到系统的振动响应。
(2)建立齿面传动误差、载荷、闪温、振动的多目标优化模型,通过改进的PSO优化算法得到最佳修形齿面。
(3)受扭转变形影响,载荷会向动力输入端偏移,齿向应进行全修形,齿向的线性修形削弱了扭转变形影响,修形后重合度增加,因此载荷密度降低、承载传动误差幅值降低。齿廓修形降低了齿顶、齿根承受的载荷,消除了应力集中,因此齿顶、齿根闪温分布明显下降。
(4)齿轮副啮合线上相对振动和切向振动加速度要远大于齿轮横向、轴向、扭摆振动加速度,刚度激励和冲击激励是引起振动主要原因,随转速增加啮合冲击激励较刚度激励的影响更加明显,因此共振敏感性降低。多载荷承载传动误差(承载变形)的幅值反映了振动随载荷的变化趋势,修形有效降低了系统振动。修形后系统的啮合刚度降低,因此共振转速略有降低。
[1] LI Z,MAO K.The tooth profile modification in gear manufacture[J].Applied Mechanics and Materials,2008(10/11/12):317-321.
[2] 袁哲,孙志礼,王丹,等.基于遗传算法的直齿圆柱齿轮修形优化减振 [J].东北大学学报:自然科学版,2010,31(6):874-876.
YUAN Zhe,SUN Zhili, WANG Dan.GA-based optimum profile modification of spur gears for vibration damping [J].Journal of Northeastern University:Natural Science,2010,31(6):874-876.
[3] 王成,方宗德,贾海涛,等.人字齿轮修形优化设计[J].航空动力学报,2009,24(6):1433-1436.
WANG Cheng, FANG Zongde, JIA Haitao.Modification optimization of double helical gears[J].Journal of Aerospace Power,2009,24(6):1433-1436.
[4] 方宗德,沈允文.斜齿轮的抗胶合优化修形 [J].航空动力学报,1993,8(1):80-82.
FANG Zongde,SHEN Yunwen.Optimal tooth profile modification of helical gears for improving resistance to scuffing [J].Journal of Aerospace Power,1993,8(1):80-82.
[5] 尚振国,王华.宽斜齿轮修形有限元分析 [J].农业机械学报,2009,40(2):215-219.
SHANG Zhenguo,WANG Hua.Finite element analysis of modified wide helical gears [J].Transactions of the Chinese Society for Agricultural Machinery,2009,40(2):215-219.
[6] 方宗德,沈允文.斜齿轮三维修形的优化设计 [J].机械工程学报,1992,28(6):57-60.
FANG Zongde,SHEN Yunwen.Optimal design of 3-D modification of helical gear[J].Chinese Journal of Mechanical Engineering,1992,28(6):57-60.
[7] LITVIN F L,GONZALEZ-PEREZ I,FUENTES A,et al.Design,generation and stress analysis of face gear drive with helical pinion[J].Computer Methods in Applied Mechanics and Engineering,2005,194:3870-3901.
[8] LITVIN F L,FAN Q,VECCHIATO D,et al.Computerized generation and simulation of meshing of modified spur and helical gears manufactured by shaving[J].Computer Methods in Applied Mechanics and Engineering,2001,190(39):5037-5055.
[9] 方宗德.修形斜齿轮承载接触分析 [J].航空动力学报,1997,12(3):251-254.
FANG Zongde.Tooth contact analysis of modification of helical gears [J].Journal of Aerospace Power,1997,12(3):251-254.
[10]XU Hai.Development of a generalized mechanical efficiency prediction methodology for gear pairs[D].Columbus,USA:The Ohio State University,2005:113-128.
[11]方宗德.斜齿轮齿面柔度矩阵与修形的有限元计算[J].航空动力学报,1994,9(3):242-244.
FANG Zongde.Calculation on flexibility matrix and modification of helical gears by FEM [J].Journal of Aerospace Power,1994,9(3):242-244.
[12]高创宽.渐开线齿轮传动的混合弹流润滑研究 [D].太原:太原理工大学,2005:108-112.
[13]杨沛然,温诗铸.线接触弹流问题一种新的解算方法及更准确的油膜厚度公式[R].北京:清华大学,1988.
[14]李润方,王建军.齿轮系统动力学 [M].北京:科学出版社,1997:154-188.
[15]武宝林,杨素君,姚俊红.齿轮传动中啮合冲击的理论分析 [J].机械科学与技术,2003,22(1):55-57.
WU Baolin, YANG Sujun, YAO Junhong.Theoretical analysis on meshing impact of involute gears [J].Mechanical Science and Technology for Aerospace Engineering,2003,22(1):55-57.
[16]蒋进科,方宗德,苏进展.基于承载传动误差幅值最小的斜齿轮齿面修形优化设计 [J].航空动力学报,2013,28(7):1637-1643.
JIANG Jinke,FANG Zongde,SU Jinzhan.Optimal design of modified helical gear tooth surfaces based on the minimum amplitude of loaded transmission error[J].Journal of Aerospace Power,2013,28(7):1637-1642.
[17]龚纯,王正林.精通Matlab最优化计算 [M].北京:电子工业出版社,2009:296-299.

