混合能量电子辐照聚酰亚胺的带电特性
刘 婧,张海波
(西安交通大学电子科学与技术系,710049,西安)
空间辐照环境中,混合能量电子辐照聚合物形成的电荷积累会影响航天器正常工作,混合能量电子辐照聚合物的带电特性和航天器带电是空间等离子体与物质相互作用的一个重要研究方向[1-3]。地球磁暴环境中电子能量分布在数十keV到数百keV,是导致航天器带电和静放电的主要成因。聚酰亚胺常被作为热涂层用于地球同步轨道卫星的电子系统和某些航天器部件中[4-9],处在地球同步轨道上的电子能量辐照聚合物的电荷积累到一定程度,就会发生静放电现象。因此,深入研究混合电子辐照聚酰亚胺的带电特性是抑制和控制静电放电的产生,降低航天器故障的基础[10-16]。近几十年来,航天器和聚合物带电问题的实验方面主要采用压力波传导和脉冲电声的方法[9]。数值模型主要以辐照诱导电导率模型[11]为主。其他的理论模型有自洽电荷输运模型等[12-14]。上述方法主要基于研究单能电子辐照聚合物的带电特性,对于研究实际的空间辐照环境存在局限性[10]。混合电子辐照聚酰亚胺的带电过程较为复杂,实验方法测量微观多量对带电特性的影响具有难度。目前,综合考虑具有样品微观参量的混合能量电子辐照聚合物的带电特性研究仍然比较少,深入研究混合电子辐照聚合物的带电特性对理解航天器故障机理具有重要科学意义和价值。
本文在单能电子辐照聚合物的输运模型[15-17]的基础上,建立了混合能量电子辐照聚合物动态带电模型。混合能量电子的散射过程采用蒙特卡罗数值模拟方法[17],电荷输运过程考虑了电荷复杂的扩散、迁移、捕获和复合。本文主要研究样品带电特性中的空间电荷分布和样品微观参量影响下的空间电位分布。
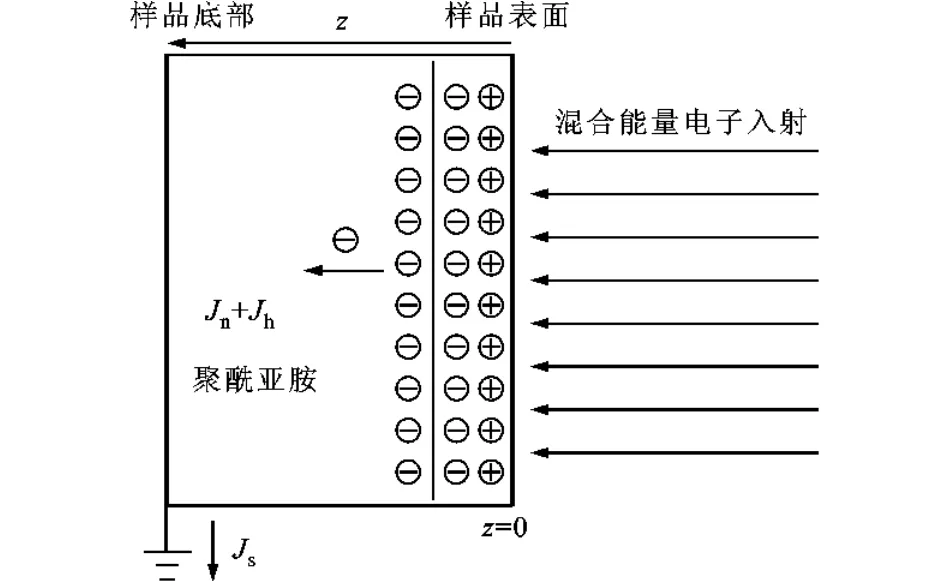
图1 混合能量电子辐照聚酰亚胺样品的示意图
1 研究方法
图1给出作为本文研究对象的聚酰亚胺在混合电子辐照的简化模型以及相关的电流密度的示意图。这里,假设聚酰亚胺的样品厚度为H,薄膜下方为接地导电衬底。混合电子照射方向为z方向。混合电子的能量范围在10keV到100keV之间,其分布符合法国国家航空航天科研局(ONERA)的地球同步轨道(GEO)电子能谱分布理论公式[10]。混合电子垂直照射聚酰亚胺样品,其中JS、Jn和Jh分别是样品电流密度、电子电流密度和空穴电流密度。
1.1 混合电子的散射
在单能电子辐照聚酰亚胺[16-17]的基础上,我们结合法国国家航空航天科研局的GEO电子能谱分布理论公式和欧空局SIRENE facility机构的地面实验模拟空间辐照环境电子能谱的实验方法,建立了基于地球同步轨道电子能谱辐照环境的混合能量电子的蒙特卡罗散射程序。
混合能量电子辐照聚酰亚胺后,会与样品的原子和分子碰撞,发生散射过程。散射过程分为弹性散射和非弹性散射两个部分。对于弹性散射过程,不同能量段的入射电子通常需要不同的弹性散射截面来描述。当入射电子的能量高于10keV时,通常用卢瑟福Rutherford散射截面来描述。由于本文的研究对象是空间混合能量电子,能量较大,所以采用如下的Rutherford微分散射截面
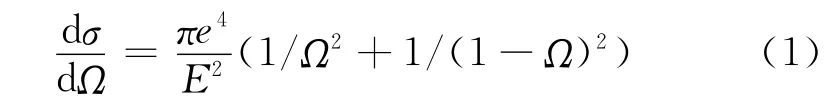
式中:σ为总的弹性散射截面,单位为cm2·atom-1;E为电子能量,单位为keV;Ω表示归一化的能量损失系数,即能量损失ΔE与总能量E的比值;e是电子电量。非弹性散射过程中,电子的能量不断损失,还可能会产生二次电子。本文采用快二次电子模型描述非弹性散射过程。入射电子在样品中的散射及运动不断地损失其能量,直至逸出样品或能量耗尽沉积在样品内部。本文所用的模型是改进的连续能量损失模型。能量损失通过Bethe公式来描述。Bethe能量损失实际上是整个散射过程能量损失的平均值,包含了非弹性散射的能量损失,产生二次电子的能量损失。Bethe能量损失公式为
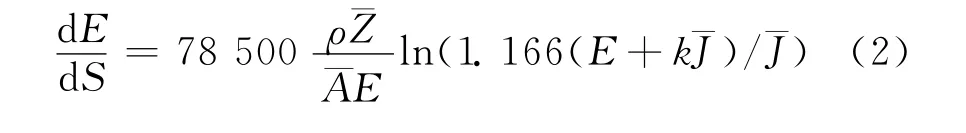
式中:ρ为材料密度;¯Z是样品平均原子序数;¯A是平均原子质量;k为修正系数;¯J为平均电离能。修正系数k由平均原子序数¯Z插值得到。对于聚酰亚胺而言,平均原子序数为4.213 7,平均原子质量为8.029 2g·mol-1,密度为1.45g·cm-3,平均电离能量为71.9eV。
混合能量电子束是通过两个电子束组合实现的。这两个电子束通过能量和束流密度进行分割来模拟类似于空间的电子束流环境。具体来说,第一个电子束流具有20keV的电子能量和250pA/cm2的束流密度。第二个电子束流符合GEO电子能谱分布,电子能量范围为10keV到100keV,束流密度为50pA/cm2[10]。论文中采用两个电子束组合来模拟类似于空间中的电子束流环境能谱的主要原因是借鉴了欧空局SIRENE facility机构的地面实验模拟空间辐照环境电子能谱的实验方法[10]。电子的弹性散射和非弹性散射过程采用蒙特卡罗模拟来实现,这部分已经在本课题组过去的工作中介绍过[15-17]。
1.2 电荷输运
混合电子入射聚合物后首先与原子发生散射和电离作用,生成大量的电子和空穴,形成局部的负电荷密集区域。电子和空穴在自洽场作用下进行迁移。捕获过程是通过Poole-Frenkel效应来实现的,Poole-Frenkel效应是介质体内局部区间隧道效应,是强电场中电荷脱陷的原因之一。另外,聚合物中的电子空穴对还有一定的概率发生复合。电荷在扩散、迁移、捕获、复合共同作用下的运动过程就是电荷输运过程。带负电荷区域在电荷输运作用下,会在材料表层和深层形成一定的空间电荷分布。
由于辐照是非聚焦类型的,在样品表面横向线方向保持不变,文中只考虑混合电子辐照聚合物沿样品深度方向(即z方向)的影响。假设样品内部自由电子浓度n(z,t)、捕获电子浓度nT(z,t)、自由空穴浓度h(z,t)、捕获空穴浓度hT(z,t)、电子电流密度Jn(z,t)、空穴电流密度Jh(z,t)、空间电位分布V(z,t)以及空间电场分布E(z,t)满足由电流连续性方程、电荷输运方程、泊松方程和捕获方程组成的方程组[15-17]
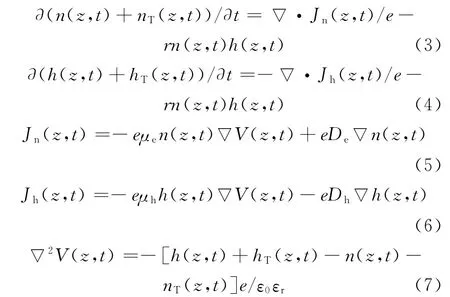
式中:e为电子电量,1.6×10-19C;ε0是真空介电常数;εr是样品相对介电常数,对于聚酰亚胺取3.45;r是电子空穴的复合率,文中默认的数值为10-15cm3·s-1;μe和μh分别为电子的迁移率和空穴的迁移率;De和Dh分别为电子扩散系数和空穴扩散系数。电子的迁移率和扩散系数满足Nernst-Einstein方程,文中取常温300K。通常聚合物中空穴迁移率小于电子迁移率。
捕获能力的大小主要是通过捕获密度与捕获截面积乘积项所代表的捕获概率来决定的,文中不考虑去捕获的影响,这里的电荷捕获过程通过式(8)、(9)说明
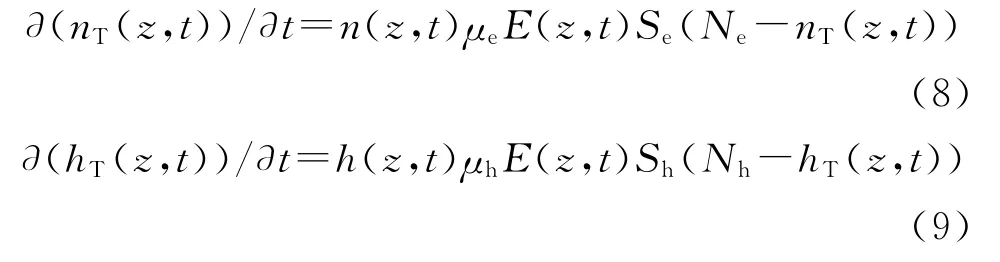
式中:Ne和Nh分别为电子捕获密度和空穴捕获密度;Se和Sh分别为电子捕获截面积和空穴捕获截面积。
2 数值模拟结果与分析
文中若无特殊说明,我们选取电子迁移率为10-11cm2·V-1·s-1[11],空穴迁移率为10-12cm2·V-1·s-1,复合概率10-15cm3·s-1,捕获密度为1014cm-3,捕获截面积为10-8cm2[13],样品厚度为25μm。聚合物的微观样品参量对带电特性的影响在目前的实验和数值方法中都没有较为详细的报道,本文对各种参量对聚合物空间电位的影响作了较为详细的描述。
2.1 空间电荷分布
聚酰亚胺的空间电荷分布特性是影响其带电过程的主要因素。已知空间电荷分布能够确定空间电位和电场分布。混合电子入射到聚合物样品后,首先与样品发生的是快速的散射过程,形成一定的散射分布。
图2a给出了电子入射能量为10、20、30、40、50和60keV,入射电子数目为10 000个的初始散射电子浓度分布图。散射形成的电子空穴分布形态相似,但是在数值上有数量级的差别。由散射电子浓度分布可以看出,能量越高电子浓度分布越平缓,峰值位置越靠近样品底部,峰值越小。当入射电子能量较高时,电子在样品中能量损失到0所需的步数变多,运动的距离也会变长。而且能量较高时,散射类型更多的是弹性散射,弹性散射不会产生二次电子和空穴,所以电子浓度会较低。值得注意的是,文中选择的入射电子能量均大于10keV,样品表面的正电荷分布几乎消失,主要原因为发生非弹性散射的位置距离样品表面较远,生成二次电子能量较低而无法运动到样品表面处并逸出,所以不会出现正电荷密度分布。
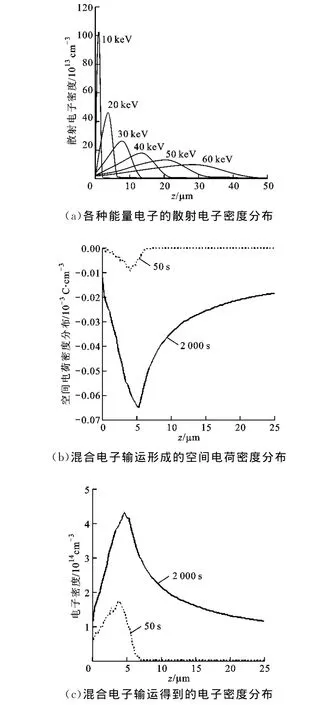
图2 混合电子辐照聚合物形成的电荷分布
图2 b所示为辐照时间50s带电暂态得到的空间电荷密度分布,以及时间2 000s对应的带电稳态情况下的空间电荷密度分布。辐照初期,电子高密度区峰值位置在样品深度4μm处,空穴的高密度峰值位置在3.2μm处。在样品内部负电场(取辐照方向为正方向,即垂直于样品表面指向底部的方向)的作用下,电子向样品底部迁移,空穴向表面迁移,而且电子的迁移率大于空穴,所以同一时刻电子分布的变化速度大于空穴。随着辐照时间增加至2 000s时,表面附近电子浓度有微弱的下降,这主要是因为电子和空穴的不断的复合[17],样品表面产生二次电子导致样品表面存在微弱的正电场,如图3所示[15-17],表面附近的电子又会不断地向表面迁移,两种作用相互抵消,所以表面处电子浓度下降的幅度很小。在样品内部随着辐照时间增加,电子积累的越来越多,电子浓度相对于照射初期有了大幅度的增加,电子的高浓度区在迁移的作用下逐渐扩大,此时已经扩展到样品底部处,峰值位置也向底面进一步移动[16-17]。
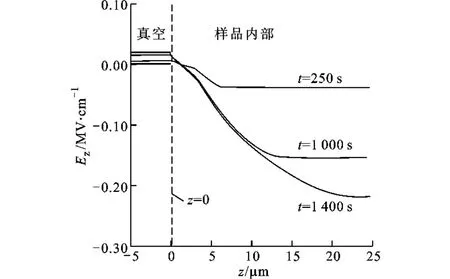
图3 不同辐照时间对应的空间电场分布
如图4所示,选取10、30、60、100keV的单能电子束对应的时变表面电位与混合能量的时变表面电位进行对比,图中给出了混合电子辐照的数值模拟结果:能量较高的电子辐照聚合物得到的表面电位值小于能量较低的电子得到的表面电位;能量较高电子的表面电位的暂态时间相对能量较低电子的表面电位暂态时间要长,积累的电荷量和表面电位较低。但是必须指出,在模拟中混合电子能谱中高能电子能量段的含量是有限的,占的比重较小。因此,高能电子能量段对带电平衡所需要的时间和降低带电平衡时的电荷积累量有一定的影响。
图4 不同能量电子的表面电位随时间的变化
2.2 样品参量对空间电位的影响
样品参量可以明显地影响带电特性。下面以空间电位分布为例分析聚酰亚胺样品参量对带电特性的影响。如图5所示,样品厚度对空间电位的影响是较为明显的,对于混合电子辐照聚酰亚胺的情况,空间电位会随着样品厚度的增加而负电位增高,如图2a所示,样品厚度为25μm时,混合电子中大于50keV的电子会穿透整个样品到达衬底,因而,25μm样品的空间电位整体要低于40μm和50μm样品的空间电位。
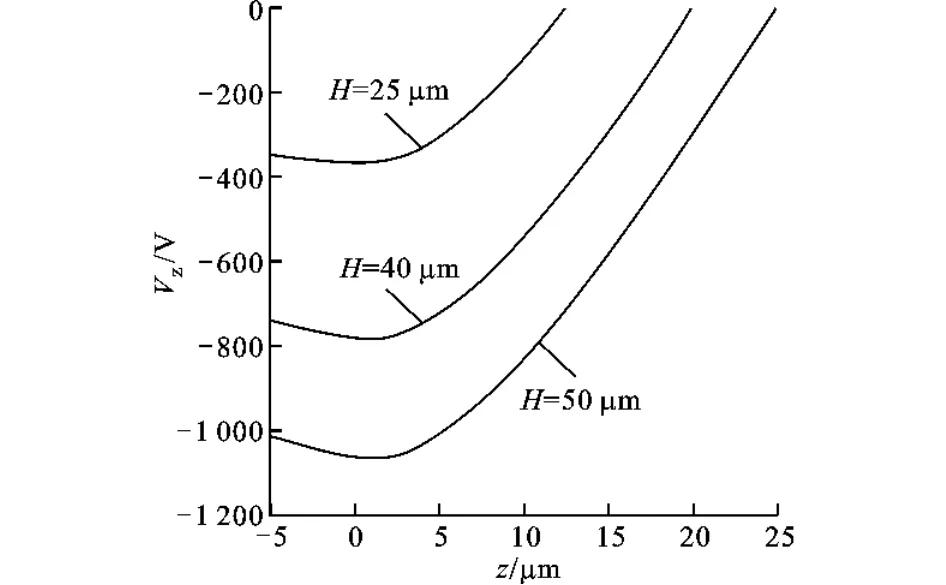
图5 不同样品厚度对应的空间电位分布
图6 给出了空间电位随捕获密度的变化。由图可见,空间电位沿混合电子辐照z方向先缓慢下降,再急剧增大到接地点电位。空间电位值总体上随捕获密度NT的增大而负电位升高,当捕获密度NT小于1014cm-3时,随着捕获密度的增大,空间电位的升高不太明显。原因是文中的捕获截面是定量,当捕获密度较小(NT<1014cm-3)时,捕获概率较小,聚酰亚胺样品内被捕获的电子数量较少,相应得到的空间电位也相对较低。当捕获密度NT>4×1014cm-3时,空间电位有相对较大的变化,更多的电子被捕获,导致空间负电位升高。
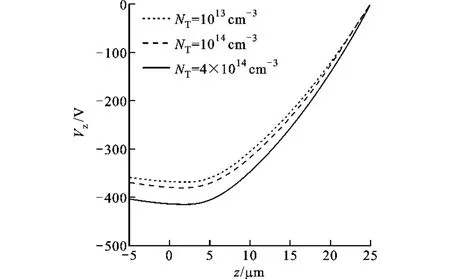
图6 不同捕获密度对应的空间电位分布
类似地,电子迁移率也可以影响空间电位。如图7所示,空间电位沿电子辐照z方向先缓慢下降,再急剧增大到接地点电位值。对于聚酰亚胺负带电情况,空间电位随电子迁移率的降低而负电位升高。原因是电子迁移率越小,电子的迁移速度就会越小,带电的动态过程就会相应变长,样品内沉积的电子浓度会随电子迁移率的降低而增大,因而样品的空间负电荷位置也会随电子迁移率减小而升高。

图7 不同电子迁移率对应的空间电位分布
3 结 论
本文研究了混合电子辐照聚酰亚胺的带电特性,主要得到以下结论:聚合物空间电位随样品厚度的增大而负电位升高,随捕获密度的增大而负电位升高,随电子迁移率的增大而负电位降低;样品厚度的影响远大于电子迁移率和捕获密度对空间电位的影响。由于混合电子中包含大量的高能电子,高能电子也会对带电平衡所需要的时间和带电平衡时的电荷积累量有一定的影响,因此混合电子辐照聚合物的负带电过程是由电荷输运过程中各种样品参量,例如样品厚度、捕获密度和电子迁移率共同作用和影响的。
[1] 李盛涛,李国倡,闵道敏,等.入射电子能量对低密度聚乙烯深层充电特性的影响 [J].物理学报,2013,62(5):059401-059410.
LI Shengtao,LI Guochang,MIN Daomin,et al.Influence of radiation electron energy on deep dielectric charging characteristics of low density polyethylene[J].Acta Physica Sinica,2013,62(5):059401-059410.
[2] GARRET H B,WHITTLESEY A C.Spacecraft charging:an update[J].IEEE Transactions on Plasma Science,2000,28(6):2017-2028.
[3] KOONS H,MAZUR J,LOPATIN A,et al.Spatial and temporal correlation of spacecraft surface charging in geosynchronous orbit[J].Journal of Spacecraft and Rockets,2006,43(1):178-185.
[4] MASUI H,TOYODA K,CHO M,et al.Electrostatic discharge plasma propagation speed on solar panel in simulated geosynchronous environment [J].IEEE Transactions on Plasma Science,2008,36(5):2387-2394.
[5] MATEO-VELEZ J C,INGUIMBERT V,ROUSSEL J F,et al.ESDs on solar cells-degradation,modeling,and importance of the test setup [J].IEEE Transactions on Plasma Science,2008,36(5):2395-2403.
[6] DONEGAN M M,SAMPLE J L,DENNISON J R,et al.Spacecraft coating-induced charging:a materials and modeling study of environmental extremes [J].Journal of Spacecraft and Rockets,2010,47(1):134-146.
[7] MIYAKE H,TANAKA Y,TAKADA T,et al.Characteristic of charge accumulation in glass materials under electron beam irradiation [J].IEEE Transactions on Dielectrics and Electrical Insulation,2007,14(2):520-528.
[8] SARRAILH P,MATEO-VELEZ J,ROUSSEL J,et al.Comparison of numerical and experimental investigations on the ESD onset in the inverted potential gradient situation in GEO [J].IEEE Transactions on Plasma Science,2012,40(2):368-379.
[9] TAKADA T,MIYAKE H,TANAKA Y,et al.Pulse acoustic technology for measurement of charge distribution in dielectric materials for spacecraft[J].IEEE Transactions on Plasma Science,2006,34(5):2176-2184.
[10] MOLINIE P,DESSANTE P,HANNA R,et al.Polyimide and FEP charging behavior under multienergetic electron-beam irradiation [J].IEEE Transactions on Electrical Insulation,2012,19(4):1215-1220.
[11]SESSLER G M.Charge dynamics in irradiated polymers[J].IEEE Transactions on Electrical Insulation,1992,27(5):961-973.
[12]GRISERI V,PERRIN C,FUKUNAGA K,et al.Space-charge detection and behavior analysis in electron irradiated polymers [J].IEEE Transactions on Plasma Science,2006,34(5):2185-2190.
[13]LE ROY S,BAUDOIN F,GRISERI V,et al.Charge transport modelling in electron-beam irradiated dielectrics:a model for polyethylene [J].Journal of Physics:D Applied Physics,2010,43(31):315402.
[14]YASUDA M,KAINUMA Y,KAWATA H,et al.Time-dependent charge distributions in polymer films under electron beam irradiation[J].Journal of Applied Physics,2008,104(12):124904-124905.
[15]FENG Guobao,CAO Meng,YAN Liping, et al.Combined effects of sample parameters on polymer charging due to electron irradiation: a contour simulation[J].Micron,2013,52/53:62-66.
[16]CAO Meng,WANG Fang,LIU Ling,et al.Charging dynamics of polymer due to electron irradiation:a simultaneous scattering-transport model and preliminary results [J].Chinese Physics:B,2012,21(12):127901-127907.
[17]李维勤,张海波.低能电子束照射接地绝缘薄膜的负带电过程 [J].物理学报,2008,57(5):3219-3229.
LI Weiqin,ZHANG Haibo.Negative charging process of a grounded insulating thin film under low-energy electron beam irradiation [J].Acta Physica Sinica,2008,57(5):3219-3229.
[本刊相关文献链接]
张振军,郑晓泉,武文斌,等.不同温度下聚酰亚胺真空直流沿 面 闪 络 特 性.2014,43(4):47-51.[doi:10.7652/xjtuxb 201404009]
张振军,苗军,王学强,等.改性聚酰亚胺的真空直流沿面闪络特性.2013,47(4):51-56.[doi:10.7652/xjtuxb201304010]
高扬,王小鹏,陈天宁.可降解聚合物溶胀性能对给药系统释药效果的影响.2012,46(1):114-119.[doi:10.7652/xjtuxb 201201021]
何良,李盛涛,张拓.TiO2/Al2O3-Al2O3-TiO2/Al2O3绝缘结构的真空沿面闪络特性.2012,46(2):93-99.[doi:10.7652/xjtuxb201202016]
曹猛,李瀛台,张海波.厚样品电子断层成像中的电子透过率非线性效应.2011,45(6):50-54.[doi:10.7652/xjtuxb2011 06009]
晨曦,王霞,吴锴,等.电压反转极性对温度梯度场下聚乙烯内空间 电 荷 的 影 响.2011,45(10):54-58.[doi:10.7652/xjtuxb201110010]
朱壮晖,周亮,周洪波,等.聚酰亚胺基柔性神经微电极的优化.2010,44(7):85-89.[doi:10.7652/xjtuxb201007019]
陈曦,王霞,吴锴,等.极性反转时间对聚乙烯中空间电荷及瞬态电场的影响.2010,44(10):91-95.[doi:10.7652/xjtuxb 201010020]
景素芳,庞宣明,陈晓南.电致动聚合物致动器的动态响应研究.2009,43(11):47-50.[doi:10.7652/xjtuxb200911010]
夏冬梅,庞宣明,陈晓南,等.电致动聚合物驱动的无阀微泵的 设 计 与 制 作.2009,43(7):92-95.[doi:10.7652/xjtuxb 200907020]

