双/多基地合成孔径雷达前视三维分辨力研究及运动参数设计
孟自强,李亚超,李浩林,邢孟道,保 铮
(西安电子科技大学雷达信号处理国家重点实验室,710071,西安)
高空高速双/多基地合成孔径雷达(SAR)协同组网成像构型在接收机前视模式下具有潜在的前视三维成像能力,作为未来合成孔径雷达的一种发展趋势,在军事对地侦察、无人机协同作战以及民用环境监测等领域具有巨大的应用潜力[1-2]。因具备收发平台分置、几何关系配置灵活和抗干扰能力强等特点,双/多基地雷达的协同组网技术引起了越来越多的关注。
不同的SAR构型会对成像机理、成像性能以及回波信号特性产生影响,因此需要对不同构型下的SAR成像机理、成像性能和回波信号特性进行研究,从理论上反映场景的成像可能性及构型对目标的分辨能力。作为一种双基雷达组网方式,双基前视圆周SAR相对于传统单/双基直线SAR,在运动过程中可以对正前方目标进行多视角观测[3],在获得距离和方位向二维分辨力的同时又可得到目标的高度维信息[4-5]。
本文以双基前视圆周SAR(BF-CSAR)为研究对象,基于文献[6-8]中的方法,对双/多基地SAR的前视三维成像能力进行了研究,建立了运动几何关系,并根据梯度法和模糊函数理论,给出了场景任意位置点目标分辨特性的精确解析式;仿真得到的分辨特性曲线验证了分析方法的有效性和场景成像可能性,以便选取最佳成像区域和飞行时段。本文对影响成像分辨力的主要运动参数进行了设计,为今后开展双/多基地SAR构型下整体系统设计和前视三维成像算法的研究奠定了理论基础。本文的研究结果,可应用于双/多基地SAR协同组网成像构型的性能研究。
1 BF-CSAR前视三维成像能力分析
传统的直线SAR只能形成二维分辨力,不能反映目标高度对雷达与目标间斜距的贡献,而传统的单基圆周SAR可具备三维成像能力[3]。本文基于单基圆周SAR的运动特性,重点分析双基前视圆周SAR构型下的前视三维分辨能力。
在双基前视圆周SAR构型下,场景中心位于坐标原点,发射机T以场景中心为圆心,以雷达在目标平面的垂足到场景中心的距离为半径作逆时针匀速圆周运动,波束中心指向场景中心;接收机R沿y轴方向飞行,前视接收成像区域回波信号;发、收机飞行高度分别为HT和HR,发射机运行圆周半径为RT,角速度为ω,接收机飞行速度为VR;两波束共同覆盖范围内存在点目标 P(x,y,z(x,y)),其中z(x,y)表示目标高度,发射机、接收机的波束照射范围分别为A、B区域。双基前视圆周SAR的运动几何关系如图1所示。本文为突出重点、简化推导,将收、发机飞行高度均设为常量。
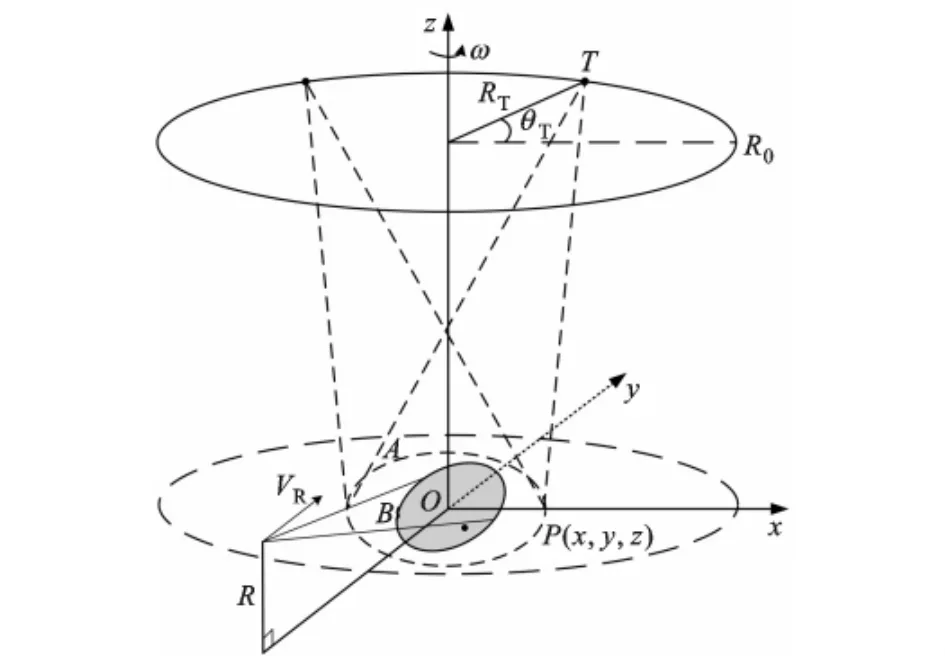
图1 双基前视圆周SAR的运动几何关系示意图
定义发射机位于图中T0位置的时刻为方位0时刻,此时接收机位于(xR0,yR0,HR)。在某一方位η时刻,发射机旋转角度为θT,点目标到两平台的瞬时斜距分别为dT,η和dR,η,此时雷达到目标之间的双基斜距可表示为
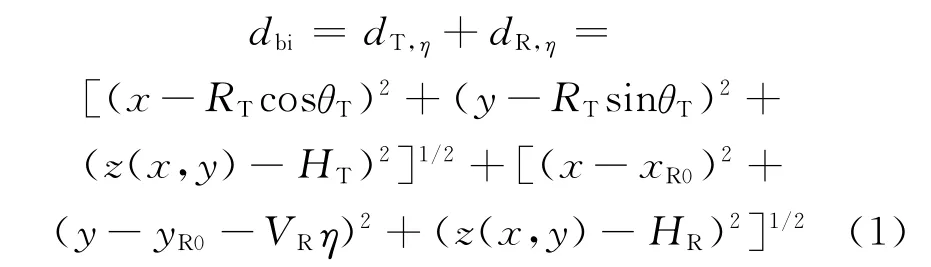
式中:下标bi表示双基平台。
假设地形高度起伏幅度远小于雷达至目标的距离,定义θ1和θ2分别表示发、收机相对于目标的俯视角,则式(1)存在如下近似
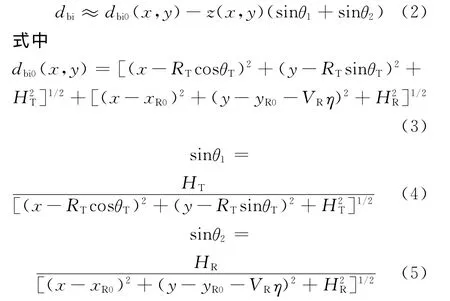
假设成像区域的目标分布函数为f(x,y),雷达发射信号为p(t),则雷达发射机在旋转角度为θT、距离时间为t时获得的SAR回波信号为
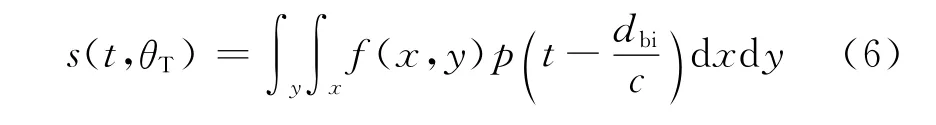
式中:c为光速。对式(6)取傅里叶变换,可得到
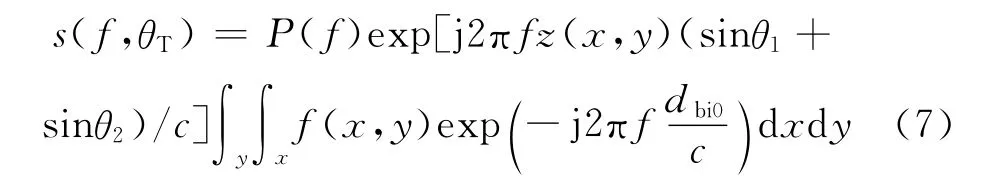
式中:P(f)为发射信号p(t)的频谱;exp[j2πfz(x,y)(sinθ1+sinθ2)/c]表示目标高度在收、发平台与目标距离连线上的投影所导致的信号相位偏移,当不存在此项时即可利用常规算法反解出目标分布函数f(x,y),此项的存在会导致目标区域的图像散焦。如果在对目标区域成像前,先对高度z(x,y)处的信号进行相位补偿,得到补偿后的接收信号
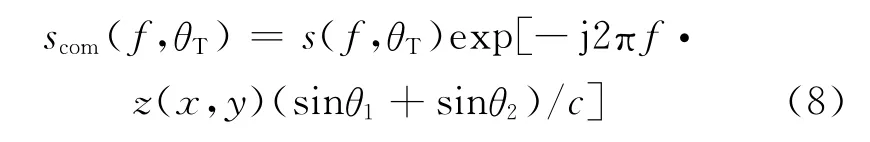
再对相位补偿后的数据进行成像,即可在不同高度z(x,y)处获得聚焦的成像结果。为实现对该项的补偿,可采用迭代搜索取最大相关值的方法,也可采用投影空间转换的思想[9]计算得到目标的高度参量,从而构造相位补偿函数。
由以上分析可知,双基前视圆周SAR可实现正前方目标的三维成像,相对传统单/双基直线SAR及单基圆周SAR,具有独特优势。
2 分辨特性研究
基于前文对双基前视圆周SAR三维成像能力的分析,本节从地距分辨力、多普勒分辨力以及高度向分辨力3个方面进行分析和讨论。首先从斜距平面内分析二维分辨特性,然后投影到水平面上得到水平面内相应的地距分辨力和多普勒分辨力,再从模糊函数的角度分析高度向分辨力,最后给出三维分辨力的理论精确解析式并分析指出影响分辨力的参量。如前文所述,相对于传统直线SAR的二维分辨能力,双基前视圆周SAR的优势在于对不同高度目标的分辨能力,所以这里重点分析高度向分辨力。
2.1 地距分辨力
利用文献[10]的梯度理论,方位η时刻的地距分辨力可表示为
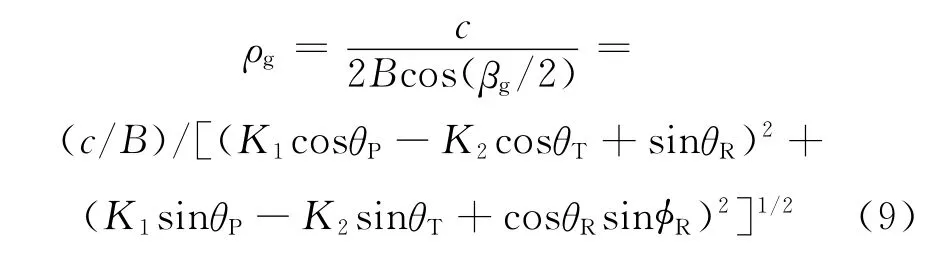
式中:B为信号带宽;βg为双基夹角β在水平面内的投影,下标g表示地平面;θP表示目标与O的连线与x轴的夹角,如图2所示;θR和φR分别为接收机相对目标的瞬时斜视角和瞬时下视角,可表示如下

其中,φ为雷达下视角,φT表示发射机相对目标的瞬时视角,δ表示图2中三角形ΔPOT′中线段OT′、OP之间的夹角,T′为发射机T在水平面的投影,α为线段PO、PT′之间的夹角。角度φ、φT、δ及α可表示如下
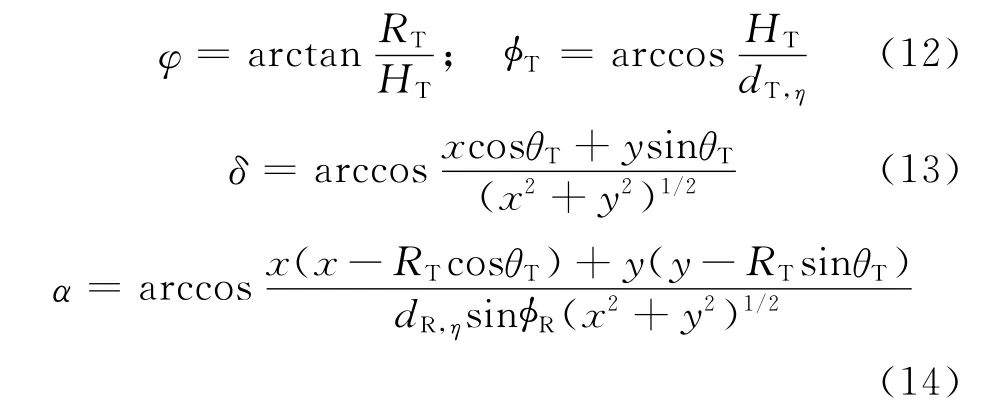
不失一般性,当点目标P位于原点时,ΔPOT′则退化为单个点,此时令cosδ=0,cosα=0。
地距分辨力ρg反映了系统构型在水平面内分辨2个目标的能力,在给定发射信号带宽B时,ρg与投影角βg有关。对于某一点目标,在不同的方位时刻,相对收发机的斜视角和雷达视角数值也不相同,即ρg具有方位时变性,而对于不同位置的点目标,目标参数θp、φT、θR、φR等也会发生变化,即ρg又具有空变性。
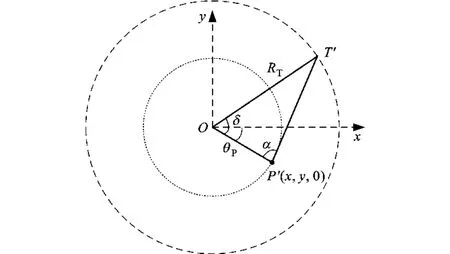
图2 发射机水平面投影几何关系
2.2 多普勒分辨力
多普勒分辨力可表示为
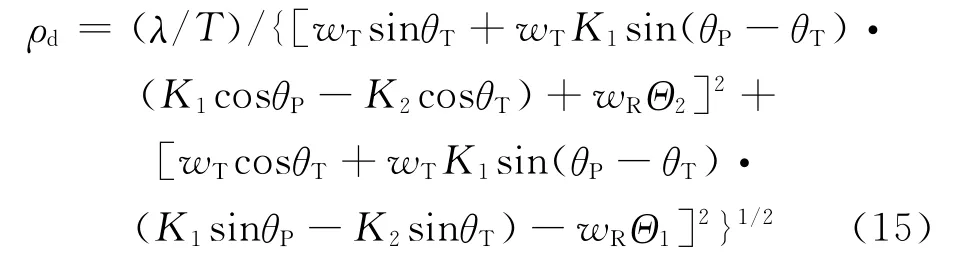
式中:T为相干积累时间;wT和wR表示点目标相对于发射机和接收机的瞬时角速度;Θ1和Θ2为角系数。
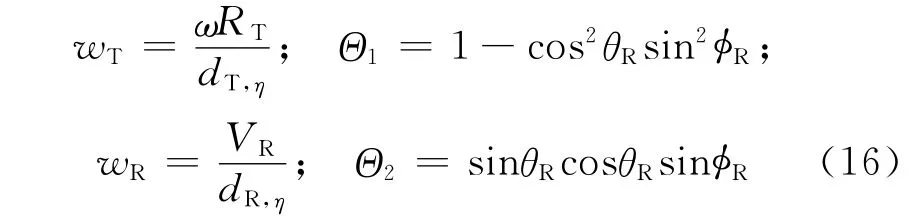
多普勒分辨力ρd与信号波长λ、相干积累时间T、运动平台的瞬时角频率以及收发平台角度等参数有关。与地距分辨力类似,多普勒分辨力也具有方位时变性和位置空变性。
2.3 高度向分辨力
本文借助文献[11]中模糊函数的概念对BFCSAR的高度向分辨力进行分析研究。该构型下的广义模糊函数可写为
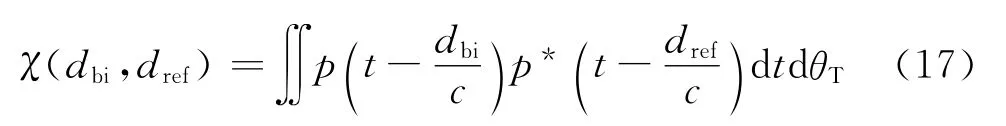
式中:dref为参考点dref(x0,y0,z0(x,y))到收发机两端的距离和,类比式(2),dref存在如下近似
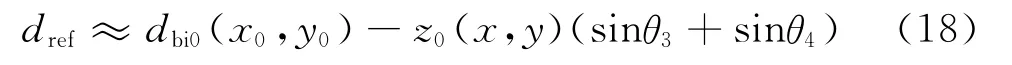
式中:θ3、θ4分别为发、收机相对于参考点的俯视角。
根据帕斯瓦尔定理,式(15)又可表示如下
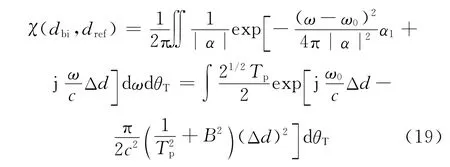
式中:Tp表示信号脉冲宽度;B为信号带宽;α1=;α=1/+j B/Tp。
高度向分辨力可由以下归一化模糊函数得到
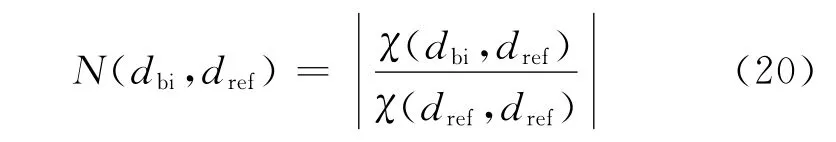
假设散射点与参考点的横纵坐标均相同,即x=y=x0=y0=0,记z(x,y)=z,z0(x,y)=z0,并令Δd=dbi-dref=Δh(sinθ1+sinθ2),Δh=z-z0,将Δd代入式(18),可得到如下关系
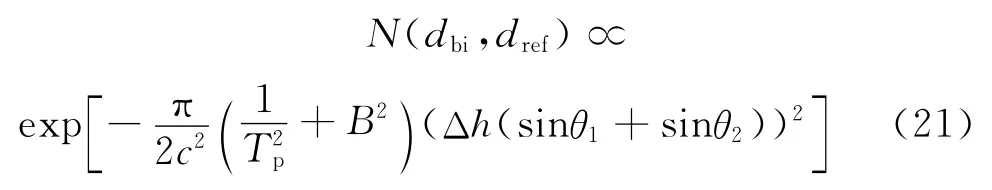
定义 N(dbi,dref)衰减至e-1时的 Δh 为 BFCSAR的高度向分辨力[11],考虑到雷达信号BTp≫1的特性,则高度向分辨力为
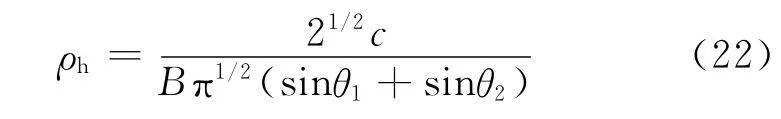
ρh反映了系统构型在高度维分辨2个目标的能力。由式(22)可知:θ1表示雷达下视角φ的余角;sinθ2是η的函数,表示接收机平台运行高度在接收机相对场景中心斜距上的投影。因此,在给定发射信号带宽B时,ρh既受到发射机平台下视角φ的影响,同时也随方位时间变化;与水平面方向分辨力(包括ρg和ρa)不同的是,ρh与目标参数θp、φT、θR、φR等无关,即ρh不具有位置空变性。
上述对ρg、ρd和ρh的理论表达式,可普适地用于在发射机处于不同旋转角度θT下对场景任意位置点目标的双基前视成像。发射机旋转角度在0°~360°变化,按照每个阶段90°划分,可分为4个不同阶段(分别称为1、2、3、4阶段),在每个阶段内场景中点目标分辨力特性各不相同,下面将进行详细分析和仿真验证。
根据ρg和ρd的方位时变性和空变性以及ρh的方位时变性特点可知:场景中存在最佳成像区域,运动平台也会存在最佳飞行时段。由于ρd理论值很小[12],在发射机运行周期内变化也很小,对成像影响较大的是ρg,因此本文主要针对ρg分析最佳成像区域和最佳飞行时段。根据式(9)和(15),ρg和ρd与目标高度无关,故可将各个点目标向水平面投影并按照x(横坐标)、y(纵坐标)轴方向划分为4个象限。由式(9)可知:在同一方位时刻,场景中目标纵坐标的增大会引起ρg减小;位于y轴上的点目标的ρg在第1、2阶段单调递增,在第2、3阶段单调递减,且在旋转角度270°处达到最小。不在y轴上的点目标的ρg,其最优时刻会有所偏移。关于ρh,由式(22)可知:当发射机在运行过程中,接收机运行至目标场景正上方时,高度向分辨力达到最优。
基于以上理论分析,可根据实际具体分辨力的要求选择合适的成像区域或平台飞行时段。关于场景中不同位置点目标和不同飞行时段的分辨特性在后面进行了仿真和分析。
3 分辨特性仿真及分析
为使分析更具普遍性和适用性,这里选取位于场景中心和不同象限内具有不同高度的9个目标点,取发射机处于图1中T0点时为方位0时刻,针对发射机处于不同飞行阶段的分辨特性进行了仿真,其中参数设置如表1所示。图3为三维方向上场景目标点的分布位置图,其中O点为场景中心,A、B、C、D 这4个目标点处于同一高度,E、F、G、H这4个目标点处于同一高度,场景各目标位置点的ρd和ρg的变化规律如图4所示。

表1 双基前视圆周SAR仿真参数
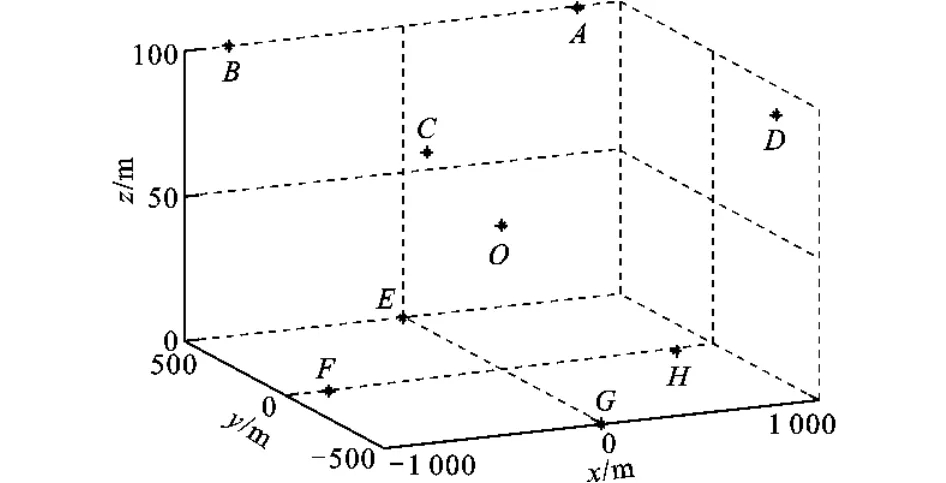
图3 场景目标点分布位置图
由图4a可以看出:关于x轴对称的F、H两目标点,其ρd变化曲线均关于旋转角度180°处对称,但变化规律相反;图4b中,分布在y轴上的目标点的ρg,在第1、4阶段分辨能力变弱,在第2、3阶段分辨能力增强,且在90°处分辨性能最差,在270°处最佳,如E、O和G目标点。
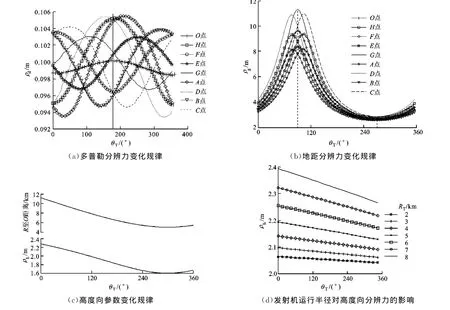
图4 场景目标位置点的分辨特性变化规律
纵坐标较大的A、B、E点处的ρg明显小于其他目标点,纵坐标最小的C、D、G点处的ρg最大。另外,场景中不在x、y轴上的目标点,其水平面方向的分辨力曲线会发生相应的偏移。例如,位于x负半轴两侧的B和C相对于F分别在145°和220°处取得最小ρd;位于y负半轴两侧的C和D相对于G分别在101°和79°处取得最大ρg。
为更好地验证ρh随旋转角度的变化规律,本文仿真时将接收机速度取为1 500m/s,接收机波束一直照射场景区域,其他参数与表1相同。由于ρh不具有空变性,所以场景中9个目标点的高度向分辨力随方位时间的变化曲线重合在一起,如图4c所示。当接收机从0时刻运行到目标场景正上方(对应图中300°)的过程中,分辨能力增强;当接收机远离目标区域时,分辨能力减弱。但应注意的是,接收机在实际前视接收过程中,一般在到达场景正上方之前就已完成对回波信号的录取,可见在实际飞行过程中高度向分辨能力在一直增强。图4d为ρh随发射机圆周半径的变化规律,发射机飞行高度不变,圆周半径从2km到8km的增大会引起雷达下视角增大,进而导致ρh变大,分辨能力减弱。
4 运动参数设计
根据以上对分辨力的分析研究和仿真验证结果,下面给出影响分辨力主要运动参数的设计思想,为后续整体系统设计和算法研究奠定基础。运动参数主要包括:波束下视角、发射机运行圆周半径、发射机圆周线速度、接收机速度、信号带宽等。
设收发平台的高度均为H,波束中心的下视角均为φ,到场景中心斜距为ds,俯仰波束宽度βr。图5是雷达俯仰照射示意图。
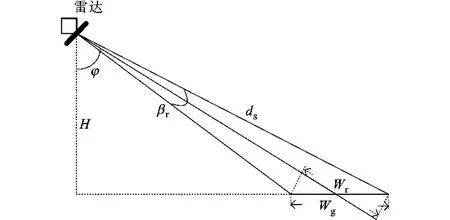
图5 雷达俯仰照射示意图
合成孔径长度可表示为
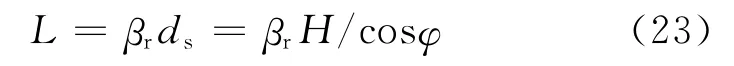
根据几何关系确定发射机运行圆周半径

以及接收机速度
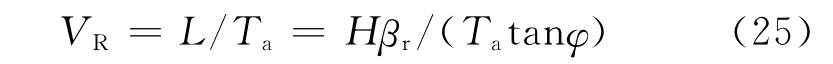
式中:Ta为合成孔径时间,可由多普勒分辨力要求确定。在Ta时间内发射机转过的角度可表示为
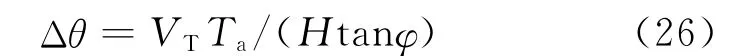
发射机平台速度可根据式(26)确定
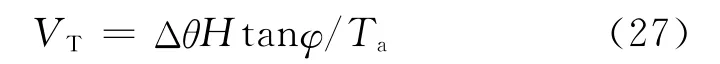
若平台高度H=10km,俯仰波束宽度βr=10°,合成孔径时间Ta=5s,合成孔径时间内Δθ=45°,为了保证目标有一定能量的散射回波,对于不同的波束下视角所对应的平台速度和发射机圆周半径的设计参数如表2所示。
由前文所述,信号带宽B主要影响地距分辨力和高度向分辨力。为确定发射信号带宽,将式(9)和式(22)重写如下

表2 平台速度和圆周半径设计参数
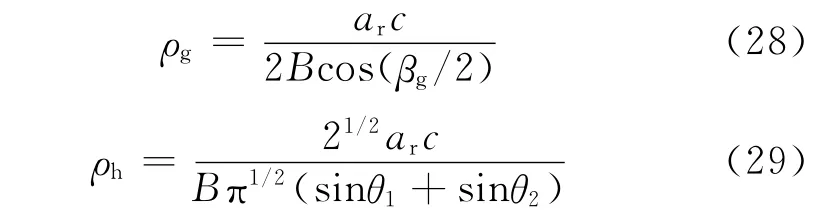
式中:ar为加权后分辨力的扩展因子,一般可取ar=1.47。由式(28)和(29)即可确定发射带宽
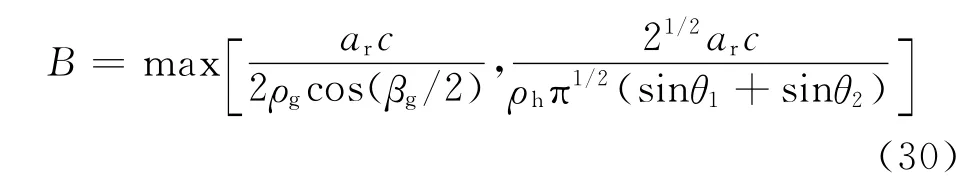
结合图1运动几何构型,sinθ1和sinθ2分别由式(4)和下式确定
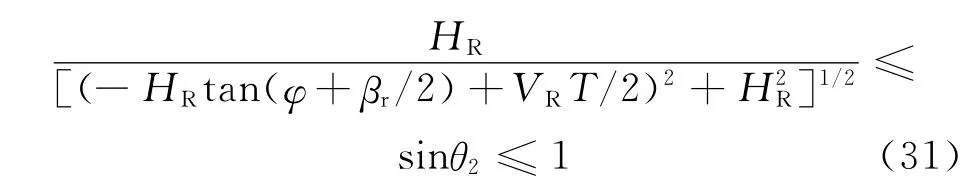
对应不同的分辨力要求,具体选择的发射信号带宽如表3所示。

表3 发射信号带宽设计参数
需要指出,在给定ρg和ρh情况下,发射信号带宽选择越宽,分辨力的富余量越大,并且允许较重的加权处理以减小旁瓣,但是频带越宽,要求的采样率就会越高,导致数据变大,系统灵敏度下降。因此,在选择频宽时要加以综合权衡。
5 结束语
相对于传统单/双基直线SAR,B/M-SAR成像构型具有高度向分辨的优势,可实现对目标的前视三维成像。本文针对高速高空B/M-SAR的成像性能和分辨特性进行了研究,可有效指导成像场景最佳成像区域和平台最佳飞行时段的选取,以及对影响分辨力主要参数的设计,为后续该构型下整体系统设计和算法研究工作提供理论依据。
[1] 闵锐.机载SAR三维成像理论及关键技术研究 [D].成都:电子科技大学,2012.
[2] 郭冠斌,方青.雷达组网技术的现状与发展 [J].雷达科学与技术,2005,3(4):193-198.
GUO Guanbin,FANG Qing.Current status and development of radar netting technique [J].Radar Science and Technology,2005,3(4):193-198.
[3] 宋千,李杨寰,梁福来,等.圆迹合成孔径雷达成像分辨力分析 [J].计算机仿真,2011,28(10):18-23.
SONG Qian,LI Yanghuan,LIANG Fulai,et al.Analysis of circular SAR time-domain imaging resolution[J].Computer Simulation,2011,28(10):18-23.
[4] PONCE O,PRATS-IRAOLA P,PINHEIRO M,et al.Fully polarimetric high-resolution 3-D imaging with circular SAR at L-band [J].IEEE Transactions on Geoscience and Remote Sensing,2014,52(6):3074-3090.
[5] LIN Yun,HONG Wen,TAN Weixian,et al.Airborne circular SAR imaging:results at P-band [C]∥Proceedings of IEEE International Geoscience and Remote Sensing Symposium.Piscataway,NJ,USA:IEEE,2012:5594-5597.
[6] QIU Xiaolan,HU Donghui.Some reflections on bistatic SAR of forward-looking configuration [J].IEEE Geoscience and Remote Sensing Letters,2008,5(4):735-739.
[7] AI Xiaofeng,ZOU Xiaohai,LIU Jin.Bistatic high range resolution profiles of precessing cone-shaped targets[J].IET Radar,Sonar & Navigation,2013,7(6):615-622.
[8] ZENG Tao,CHERNIAKOV M,LONG Teng.Generalized approach to resolution analysis in BSAR [J].IEEE Transactions on Aerospace and Electronic Systems,2005,41(2):461-474.
[9] PARK S H,KIM H T,KIM K T.Cross-range scaling algorithm for ISAR images using 2-D Fourier transform and polar mapping [J].IEEE Transactions on Geoscience and Remote Sensing,2011,49(2):868-877.
[10]CARDILLO G P.On the use of gradient to determine bistatic SAR resolution[C]∥Proceedings of Antennas and Propagation Society International Symposium.Piscataway,NJ,USA:IEEE,1990:1032-1035.
[11]ISHIMARU A,CHAN T K,KUGA Y.An imaging technique using confocal circular synthetic aperture radar [J].IEEE Transactions on Geoscience and Remote Sensing,1998,36(5):1524-1530.
[12]WU Junjie,YANG Jianyu,YANG Haiguang,et al.Optimal geometry configuration of bistatic forwardlooking SAR [C]∥Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing.Piscataway,NJ,USA:IEEE,2009:1117-1120.

