用于非规则波导传输特性分析的高效坐标变换法
倪中非,黄斌科,师振盛
(西安交通大学电子与信息工程学院,710049,西安)
波导的传输特性一直是微波工程领域的一项重要基础研究课题。随着微波传输系统的不断发展,大量性能各异的非规则截面波导应运而生,由于结构的复杂性,传统方法在研究这类新型波导的传输特性问题时面临重重困难。目前,非规则波导问题的求解大多是利用有限差分法和有限元法等数值方法直接进行求解[1-2]。由于非规则波导的截面具有不规则性,为保证计算精度,往往需要大量的剖分网格,导致计算资源消耗大、处理效率低、编程实现复杂等问题,因此如何高效、精确、方便地求解非规则波导的传输特性问题仍是目前微波工程领域的研究热点之一。
早期的传统坐标变换法以解析保角变换为基础,其关键问题在于如何确定具体的变换函数,然而这一过程通常比较困难,导致其在解决实际工程问题上的局限性很大[3]。2006年,Pendry和Leonhardt提出的坐标变换理论为新型微波器件的分析和设计提供了一条全新的思路[4]。该理论依据Maxwell方程组基于坐标变换的形式不变性,将空间坐标变换和媒质参数变换有机联系起来,使得以往复杂的分析和设计过程变得直观高效。目前,该方法已被广泛应用于随机粗糙面散射、理想匹配层(PML)吸收边界、新型微波器件设计和多尺度复杂边值问题数值仿真等领域[5-7]。
本文将坐标变换法引入到非规则截面波导的分析中,通过坐标变换,将不规则边界区域变换为规则边界区域,而区域变换的影响则通过填充变换媒质来等效,从而将原非规则波导转变为填充变换媒质的等效规则波导来处理,降低了边界处理算法的复杂度和剖分区域的网格密度,有效提高了数值计算效率。本文利用有限元法结合坐标变换法计算了椭圆波导和矩形脊波导的截止波数和场分布,并且与利用有限元法直接对原问题求解的结果进行比较,充分验证了本文方法的高效性。
1 坐标变换法基本理论
坐标变换法的理论基础为Maxwell方程组的形式不变性[8]。首先,定义一个坐标变换F:Ω→~Ω,将原空间域Ω中的所有点P映射到变换域~Ω中,记为点~P,即


当原空间Ω中的媒质无耗时,变换媒质同样为无耗媒质。
本文在分析非规则截面波导模型时,利用坐标变换法将非规则截面波导变换为规则截面波导进行数值仿真。在此取非规则波导为原空间域Ω,经坐标变换所得的规则波导为变换域~Ω。在原非规则波导中电场矢量E(r)和磁场矢量H(r)满足
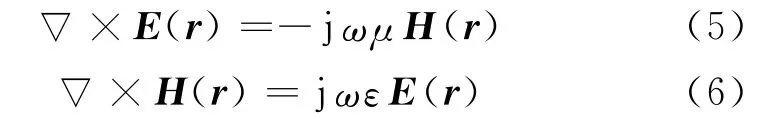
由Maxwell方程组的形式不变性可知,变换后的等效规则波导中电场、磁场满足
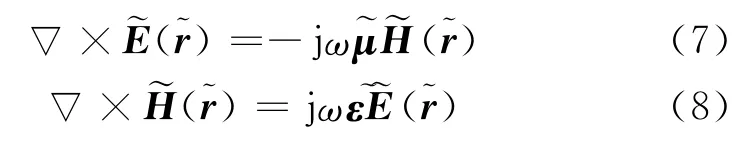
由式(5)~式(8)可知,原非规则波导和变换后等效规则波导中的电场、磁场之间存在如下关系
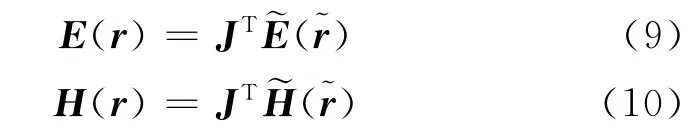
取波导轴向沿z方向,由于波导轴向的均匀性,可将三维模型简化为二维处理。在二维情况下,变换域中的纵向场方程为
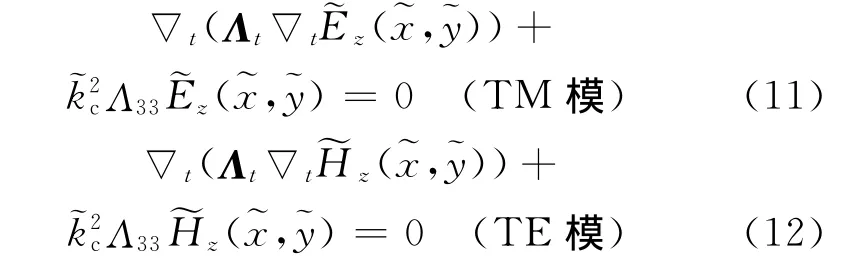
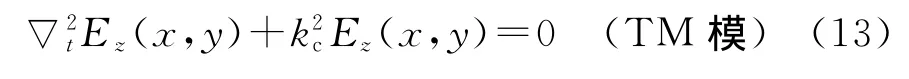
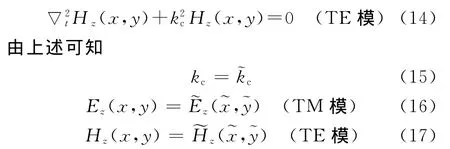
由式(15)~式(17)可见,通过求解坐标变换所得等效规则波导的截止波数和场分量),即可获得原非规则波导的传输特性。方程(11)和(12)中的截止波数和场分量)可利用有限元法转化为广义本征值问题来计算[9]
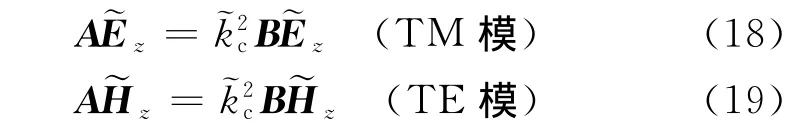
式中:A和B为有限元离散得到的稀疏矩阵。
本文在使用有限元方法计算时,剖分单元采用三角线性元,这样式(4)的Jacobian矩阵就可方便地由剖分单元的基函数和节点坐标值计算得到[10]。
2 仿真验证及分析
本文利用坐标变换法分析了椭圆波导和矩形脊波导的传输特性。通过坐标变换分别将椭圆波导和矩形脊波导转化为等效的圆波导和矩形波导,然后利用有限元法分别计算了其截止波数和纵向场分量。截止波数和纵向场分量在原波导中记为k′c、E′z(x,y)(TM 模)、H′z(x,y)(TE模),在变换后的规则波导中记为经坐标反变换后所得原非规则波导横截面上的纵向场记为Ez(x,y)和Hz(x,y),由等效波导求得的截止波数相对于原非规则波导截止波数的误差系数记为δkc)×100%,纵向场的误差系数记为δf)×100%,其中f′代表E′z(x,y)(TM 模)或者 H′z(x,y)(TE模),f″代表由Ez(x,y)或者 Hz(x,y)在原非规则波导剖分网格点上进行加权插值得到的场值。本文结果由Matlab 2012计算所得,计算机配置:内存为1GB,CPU为Celeron(R)。
2.1 椭圆波导传输特性
利用坐标变换法将空气填充的椭圆波导用填充变换媒质的圆波导来等效,Ω和~Ω分别为椭圆波导截面和等效圆波导截面,其坐标变换关系为F(r):),即
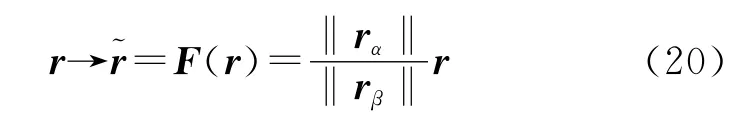
式中:rα、rβ分别为空间~Ω和Ω中边界点Pα和Pβ的位置矢量;r为空间Ω中点的位置矢量。椭圆波导到等效圆波导的坐标变换过程如图1所示。
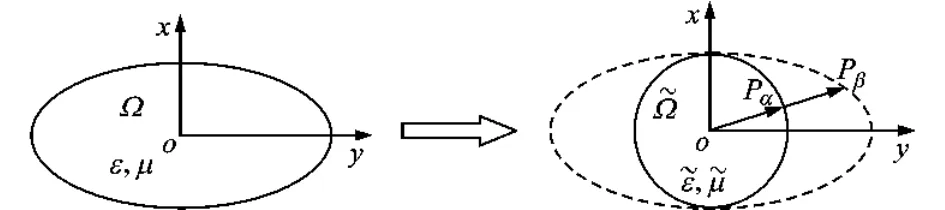
图1 椭圆波导到等效圆波导的坐标变换示意图
取椭圆波导截面的长、短半轴分别为a=10mm,b=6mm,等效圆波导截面的半径为r=6mm。为较好地逼近曲线边界,采用三角网格剖分。表1列出了椭圆波导和其等效圆波导前6个模式的截止波数及误差系数δkc和δf。表2对本文方法和传统方法的计算量和计算时间进行了对比。图2所示为椭圆波导和其等效圆波导横截面上主模TEc11模的纵向场分布。
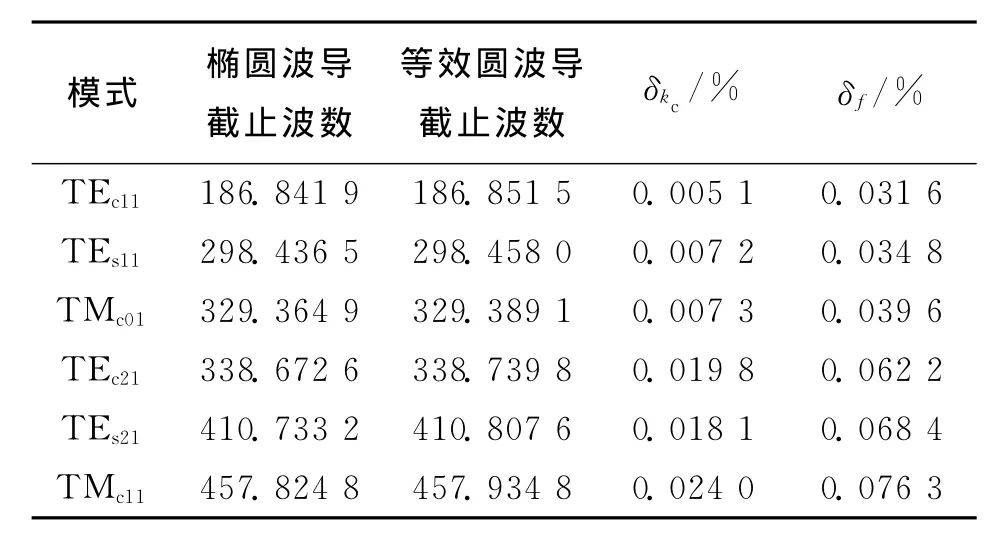
表1 椭圆波导和其等效圆波导的截止波数及相对误差

表2 本文方法和传统方法的计算量和计算时间对比
由表1可见,经坐标变换所得的圆波导和原椭圆波导的传输特性完全等效,截止波数的最大相对误差不超过3/10 000,场分布的最大相对误差不超过8/10 000。由表2可见,本文方法在计算内存和计算时间上分别比传统方法减少了近60%和50%,相比于利用有限元法直接求解椭圆波导,经坐标变换所得的等效圆波导不仅边界条件处理更为简单方便,而且能有效节省计算资源,这也是本文方法的主要优势所在。

图2 椭圆波导和其等效圆波导横截面上TEc11模的纵向场分布
2.2 矩形脊波导的传输特性
利用坐标变换法,将矩形脊波导变换为局部填充变换媒质的等效矩形波导,如图3所示。图3中坐标变换将左图中虚线框与脊所围的区域Ω映射到右图中的矩形阴影区域即变换域~Ω,坐标变换关系为
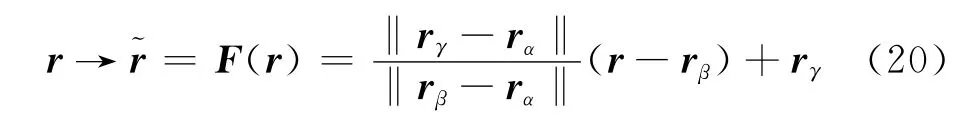
式中:rα、rβ、rγ分别为边界点Pα、Pβ、Pγ的位置矢量;r为区域Ω内点的位置矢量;变换域~Ω中填充变换媒质的参数由式(2)、式(3)计算得到。
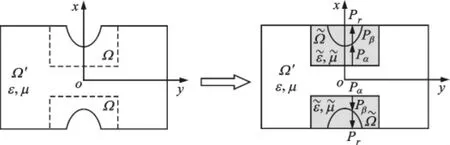
图3 矩形脊波导到等效矩形波导的坐标变换示意图
取矩形脊波导的长l、宽w为100mm、50mm,脊高度h分别为5mm、10mm和15mm;等效矩形波导的长l、宽w为100mm、50mm,填充变换媒质区域的长、宽取30mm、15mm。
表3给出了矩形脊波导和其等效矩形波导在不同脊高度下几种模式的截止波数及误差系数δkc和δf。同样,表4对本文方法和传统方法的计算量和计算时间进行了对比。
由表3可以明显看出,加脊后主模TE10模的截止波数降低,且随脊高度的增加,主模截止波数进一步减小,而TM模及TE01、TE20模的截止波数增加,从而使得矩形脊波导的工作频带变宽。由表4可知,相比于矩形脊波导复杂的导体边界,等效矩形波导的边界简单规则,可以降低空间网格的剖分密度,有效节省计算资源。
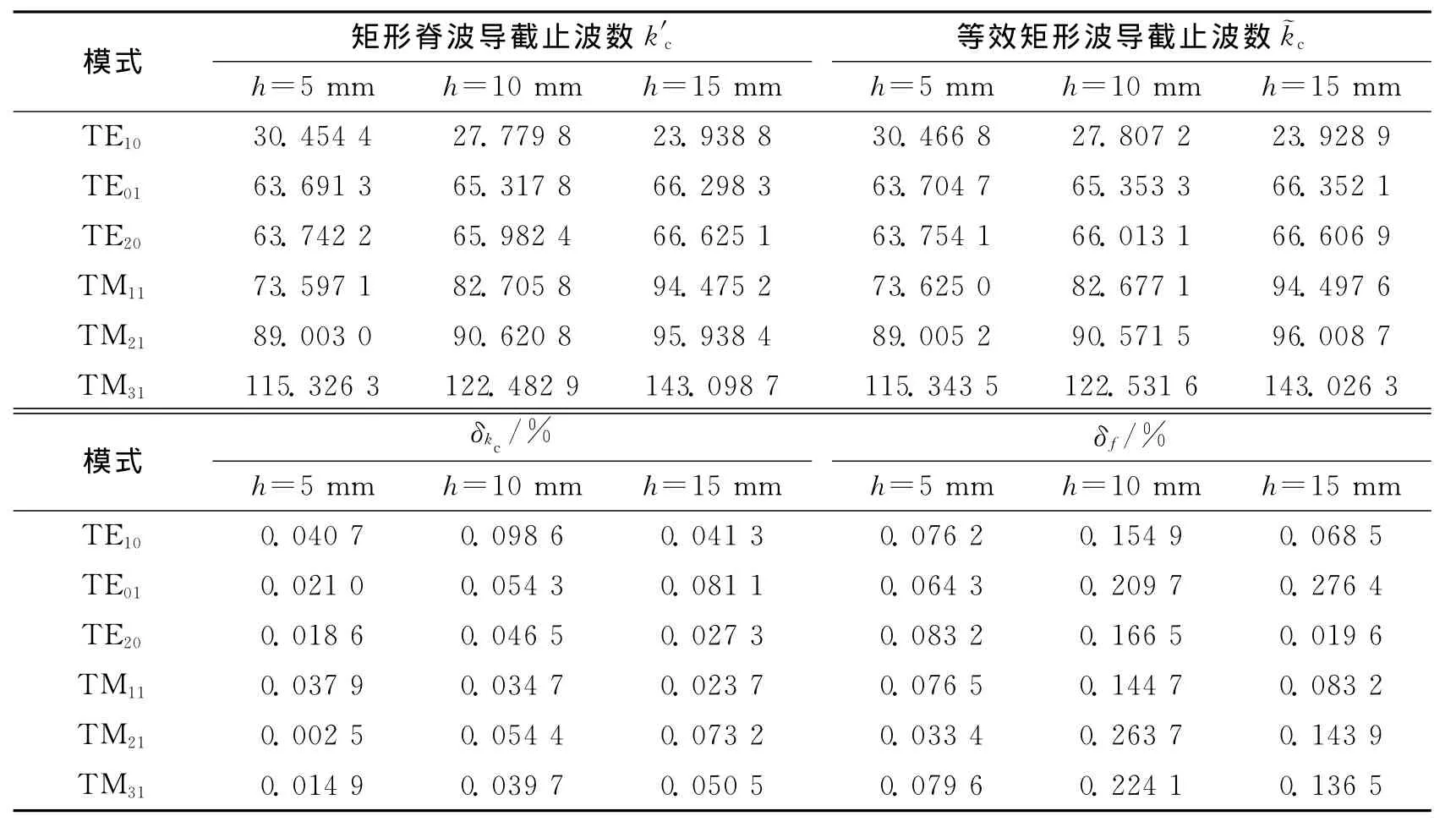
表3 3种脊高度下矩形脊波导和其等效矩形波导的截止波数及相对误差
图4所示为脊高度取10mm时,矩形脊波导和其等效矩形波导横截面上主模TE10模的纵向场分布。由图4可见,等效矩形波导中通过填充的变换媒质控制电磁场分布,使得其内部场分布和原矩形脊波导的近乎相同。
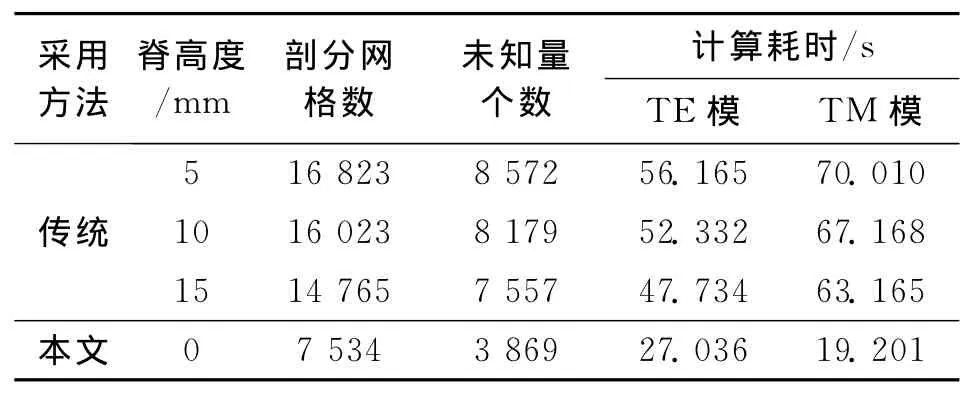
表4 本文方法和传统方法的计算量和计算时间对比

图4 矩形脊波导和其等效矩形波导横截面上TE10模的纵向场分布
值得强调的是,有限元求解时,对于取不同脊高度的情形,如果直接对矩形脊波导进行求解,每种情形都需重新建模剖分,而采用等效矩形波导时,仅建模剖分一次,每次只需重新计算填充变换媒质的参数即可,有效降低了处理过程的复杂度。
3 结 论
本文将坐标变换法引入到非规则波导传输特性问题的分析中,通过坐标变换,将非规则波导转变为填充变换媒质的等效规则波导。仿真结果表明,与传统直接对非规则波导进行数值求解相比,本文方法实现简单,在保证高精度的同时,可有效降低数值仿真的复杂度。本文方法的研究结果可应用于曲面边界、粗糙边界等复杂边值电磁问题的高效数值仿真中。
[1] 乔海亮,王玥,陈再高,等.全矢量有限差分法分析任意截面波导模式 [J].物理学报,2013,62(7):1-8.
QIAO Hailiang,WANG Yue,CHEN Zaigao,et al.Full-vectorial finite-difference analysis of modes in waveguide with arbitrary shape [J].Acta Physica Sinica,2013,62(7):1-8.
[2] 周平.脊加载椭圆波导传输特性的矢量有限元分析[J].电波科学学报,2009,24(6):1164-1167.
ZHOU Ping.Propagation characteristics analysis for ridged elliptical waveguide by vector finite element method[J].Chinese Journal of Radio Science,2009,24(6):1164-1167.
[3] 周海京,林为干,丁武,等.新型椭圆函数波导族的保角变换有限差分解法 [J].电波科学学报,1999,14(2):121-128.
ZHOU Haijing,LIN Weigan,DING Wu,et al,Conformal mapping finite difference method for analyzing a novel family of elliptic function waveguides[J].Chinese Journal of Radio Science,1999,14(2):121-128.
[4] PENDRY J B,SCHURIG D,SMITH D R.Controlling electromagnetic fields[J].Science,2006,312(5781):1780-1782.
[5] OZGUN O,KUZUOGLU M.A transformation media based approach for efficient Monte Carlo analysis of scattering from rough surfaces with objects[J].IEEE Transactions on Antennas and Propagation,2013,61(3):1352-1362.
[6] OZGUN O,KUZUOGLU M.Non-Maxwellian locallyconformal PML absorbers for finite element mesh truncation[J].IEEE Transactions on Antennas and Propagation,2007,55(3):931-937.
[7] KWON D H, WERNER D H.Transformation electromagnetics:an overview of the theory and applications [J].IEEE Antennas and Propagation Magazine,2010,52(1):24-45.
[8] MILTON G W,BRIANE M,WILLIS J R.On cloaking for elasticity and physical equations with a transformation invariant form [J].New Journal of Physics,2006,8(10):248-267.
[9] JIN Jianming.The finite element method in electromagnetics[M].New York,USA:Wiley,2002:233-236.
[10]OZGUN O,KUZUOGLU M.Form invariance of Maxwell’s equations:the pathway to novel metamaterial specifications for electromagnetic reshaping [J].IEEE Antennas and Propagation Magazine,2010,52(3):51-65.

