时滞TCP网络滑模预测主动队列管理算法

刘 胜，荆 奇

（哈尔滨工程大学自动化学院，150001，哈尔滨）

随着TCP网络规模的不断扩大和网络用户数量的高速增长，由于链路带宽、路由缓冲容量、瓶颈节点设备性能等网络资源的客观限制，网络拥塞控制成为了亟待解决的问题。在网络中间节点中实行主动队列管理（active queue management，AQM）已成为解决网络拥塞问题的主要途径之一［1］。

目前，随机早期检测算法（random early detection，RED）［2］与PI／PID［3］及其改进算法已有较为广泛的应用研究，有结构简单、适用性强的优点，但其控制机制缺少优化设计，当网络动态变化或出现参数摄动时存在鲁棒性较差的缺陷。文献［4］提出的SPIRED算法将PI和RED算法结合，在RED控制区间内加入了调节分组丢失率的PI控制器，同时也增加了算法参数调节的复杂性。

文献［4］运用动态矩阵控制设计AQM算法，将网络受到的限定转化为系统约束，运用带约束的动态矩阵控制路由缓冲队列，具有较好的鲁棒性，但是超调较大且需要预先测量阶跃响应。

滑模控制（sliding mode control，SMC）以其对于参数摄动和外部干扰具有很强鲁棒性的优点［5-6］，已经被成功应用到网络拥塞控制系统中［7］。本文运用滑模预测控制理论（sliding mode predictive control，SMPC）设计AQM算法，将网络性能需求转化为控制目标，针对网络时变时滞对系统的影响，给出了具有时滞补偿的滑模预测控制律，利用滑动模态预测模型预测网络未来动态，对滑模控制进行实时校正，在网络中存在时变长时滞的情况下具有很强的鲁棒性；分析了带有时变长时滞的TCP网络的稳定性，给出了系统渐近收敛于滑模面的充分条件。仿真结果证实了该策略的有效性。

1 TCP网络动态模型

1.1 TCP网络系统描述

文献［8］基于流体理论建立了在AQM作用下TCP动态流量模型。在忽略TCP超时重传机制前提下，获得TCP拥塞控制系统的微分方程为

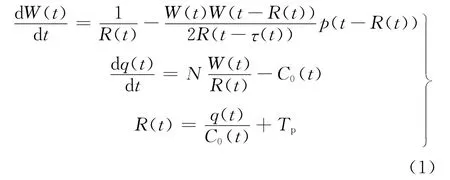
式中：W（t）为 TCP窗口尺寸；C0（t）为链路容量；N为共享同一链路的TCP连接数；p为分组丢弃概率；q为队列长度；R（t）为不确定往返时延；Tp为传输时延。

将（w，q）作为状态，p 作为输入，q作为输出，q0表示期望队列长度，则平衡点（W0，q0，p0）可通过dw（t）／dt=0和dq（t）／dt=0得到，即满足

式中：δq=q（t）-q0，δW=W （t）-W0，δp=p（t）-p0，q0、W0和p0分别为q（t）、W （t）和p（t）的期望值。令x（t）= ［δW（t） δq（t）］T，u（t）=δp（t），则式（1）可表示为

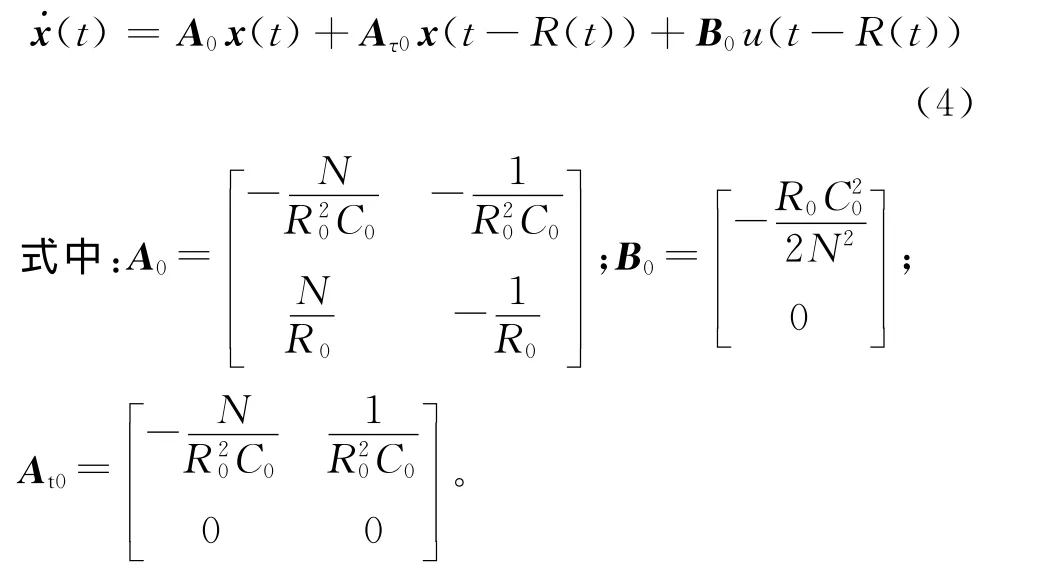
以Ts为采样周期，将系统（4）进行离散化，则系统的离散化模型为

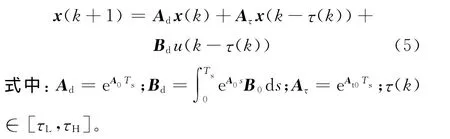
1.2 理想滑模面设计

针对TCP网络模型式（5），取线性滑模函数

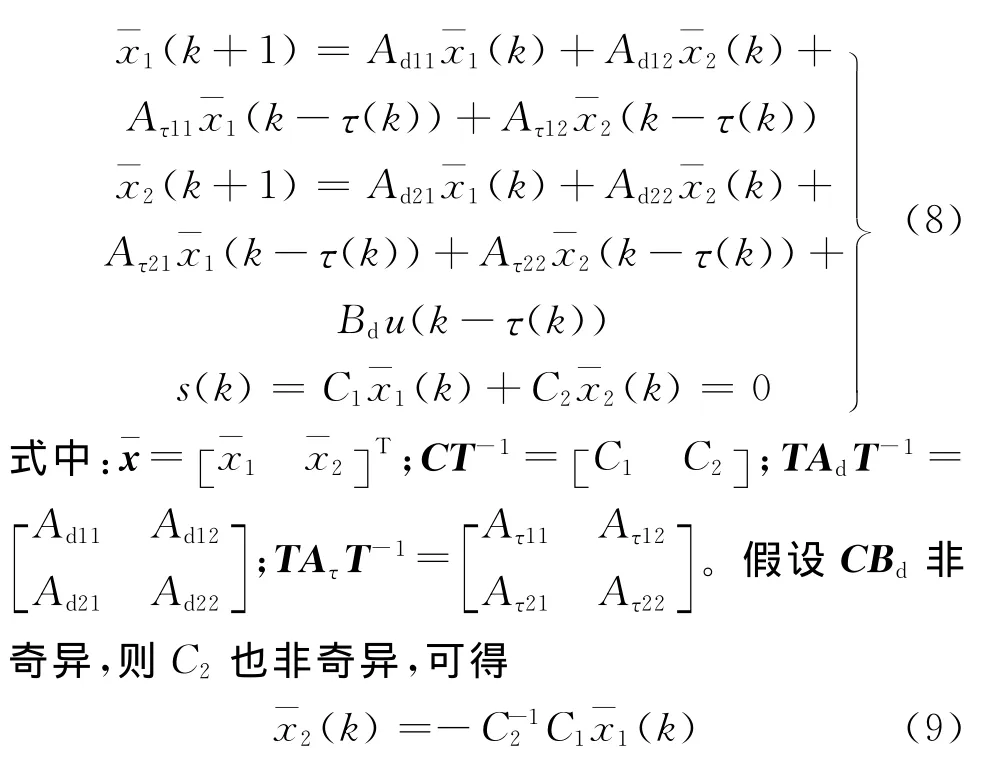
代入式（8）可得当s（k）=0时的理想滑动模态运动方程

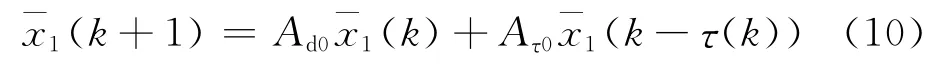
2 滑模预测AQM控制算法

2.1 滑模控制器设计

滑模预测AQM算法的主要控制要求是存在时长不确定的传输时延情况下，在控制时刻k，根据已知系统信息x（k）、s⌒（k）预测系统未来状态变化，设定预测时长为p，p≥τH，利用当前测量值s⌒（k）对未来预测值进行修正，可得系统在第k+τH+p个控制周期的预测状态为

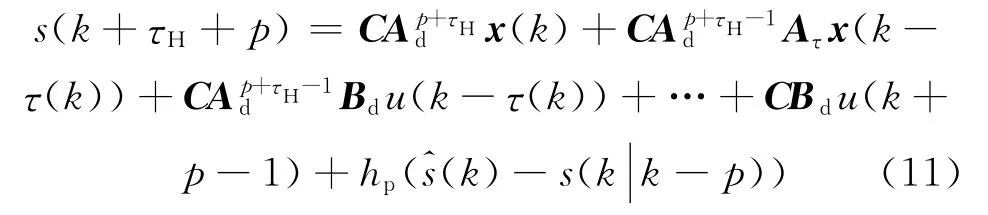
式中：hp为校正系数；s（k|k-p）为p时刻前的函数预测值。

由于网络中存在上界为τH个采样周期的传输时滞，故k时刻的控制输入不会对k+τH时刻之前的系统输出产生影响，因此系统未来p步内的滑模函数预测值为

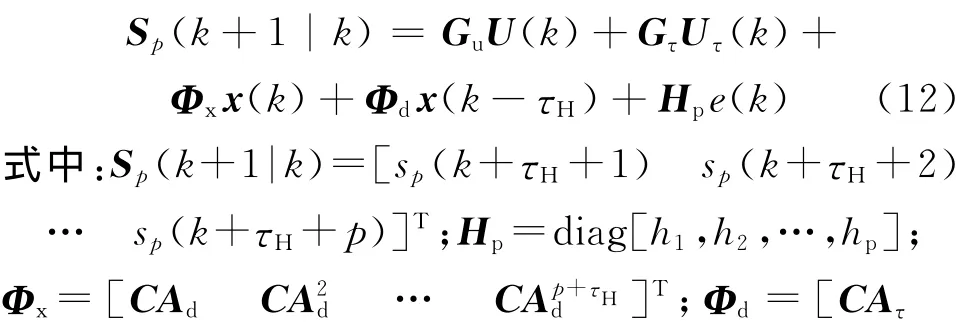
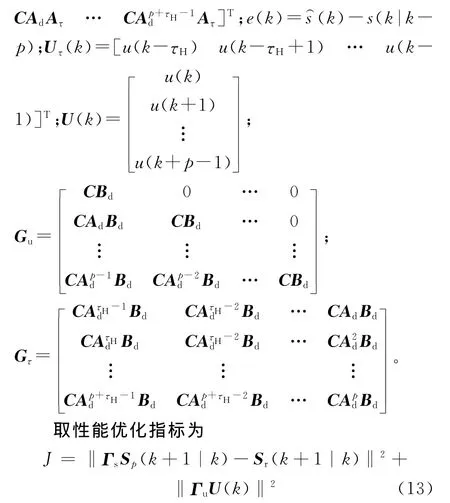
式中：Sr（k+1|k）=［sr（k+1） sr（k+2） … sr（k+p）］T；Sr（k+1|k）为滑模参考轨迹；Γs、Γu为调节控制性能的加权系数矩阵。

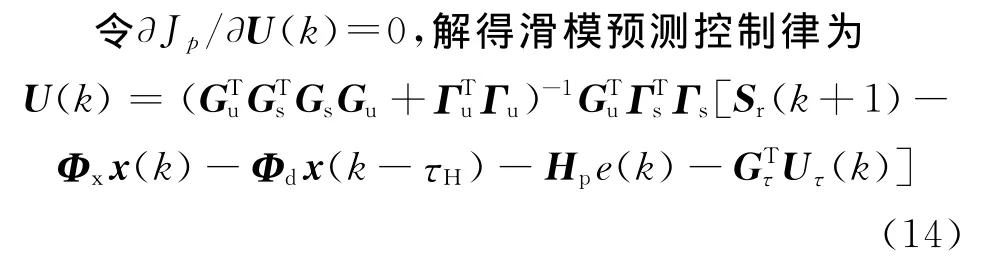
根据预测控制原理，通过式（14）可计算出未来k+p时刻内的控制量，实际只取U（k）的第一个分量，下一时刻U（k+1）通过上式递推求解，实现滚动优化，则系统k时刻控制量为

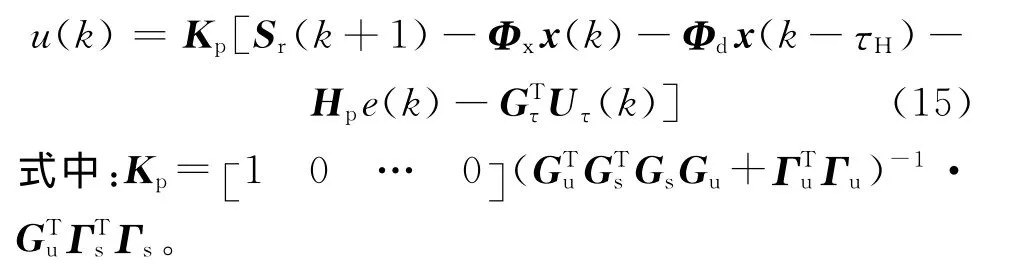
2.2 稳定性分析

为了分析基于SMPC算法的AQM策略稳定性，将描述控制律的式（15）代入被控系统（7），整理得闭环系统滑模面运动方程为

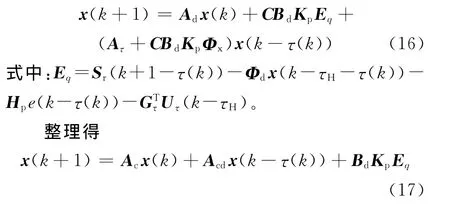
式中：Ac=Ad，Acd=Aτ+BdKpΦx。

定理1 如果存在正定对称矩阵P、R、Q使得矩阵不等式

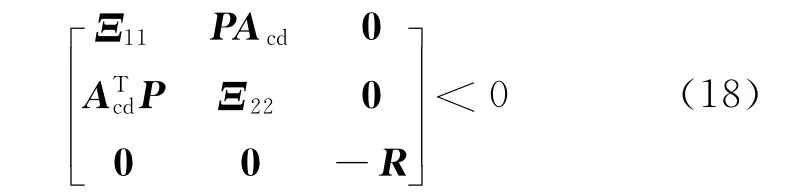
成立，则在滑模控制律（15）作用下，系统（7）渐近稳定。其中，

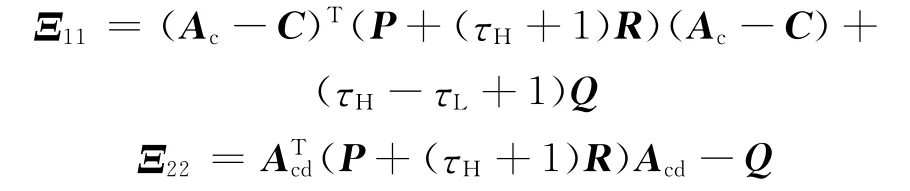
证明 在k时刻，由于系统方程中BdKpEq不包含状态x（k）、x（k-τ（k））的信息，对系统稳定性没有影响，为简化推导过程，直接研究离散时滞系统。设

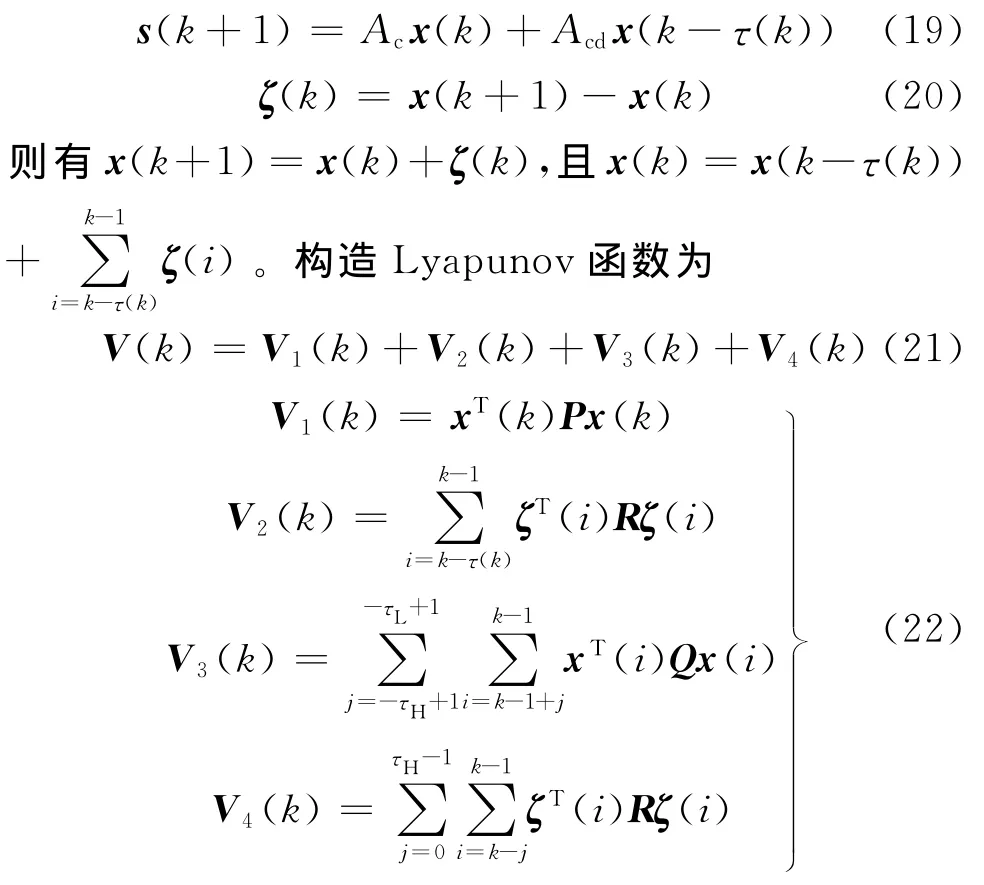
式中：P、R、Q 为待定的正定矩阵。定义 ΔV（k）=V（k+1）-V（k），则

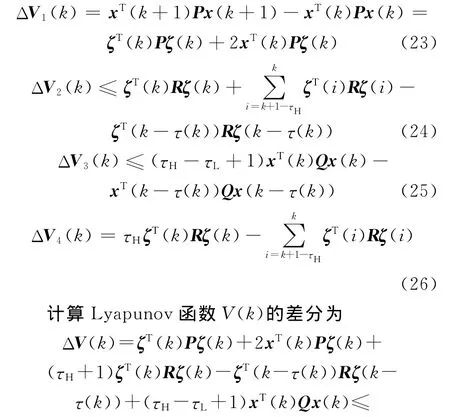
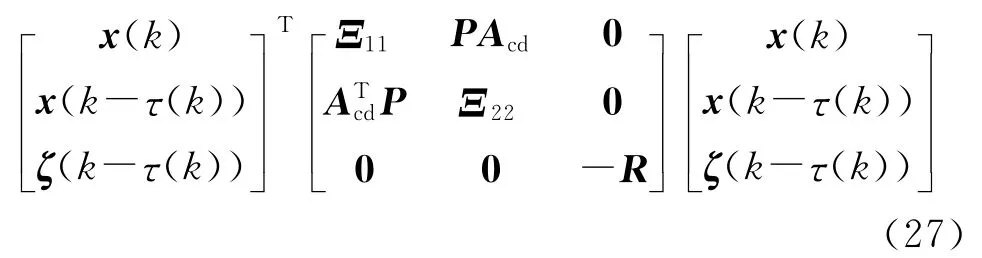
由所给条件知，若式（18）成立时ΔV（k）＜0，则系统（7）渐近稳定。定理1得证。当式（18）成立时，闭环网络系统的滑模函数必然渐近收敛并稳定于理想滑模面附近邻域，由于理想滑模面的运动品质及稳定性可由极点配置方法设计保证，因此所构成的滑模预测AQM算法鲁棒稳定，从而命题得证。

3 数字仿真与性能比较

通过仿真对滑模预测AQM控制算法性能进行验证，采用网络仿真软件NS2进行算法仿真实验。在如图1所示的网络拓扑中，路由器1与路由器2之间为瓶颈链路，其他节点之间传播时延为10ms。缓冲区的最大队列长度为400。

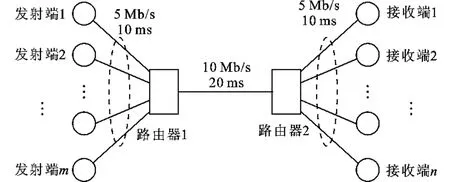
图1 网络仿真拓扑结构

设定网络环境参数为 C0=1 250包／s，N=100，q0=150包，报文缺省大小为1 000B。在瓶颈链路队列上采用SMPC算法来控制缓冲队列长度。为简化设计过程，减小计算量，取预测时域长度τ=1。Γs和Γu取为单位对角阵，采样周期Ts=0.03s，取滑模 方 程C = ［10 1］ ，控制 系 数Kp=1.3×10-5。采用PI算法、RED算法和滑模控制算法（SMC）作对比验证。PI算法参数设置为kp=4.389×10-5，ki=4.346×10-5；RED参数为qmin=110，qmax=210，权值wq=0.002；滑模控制算法（SMC）参数按文献［8］配置，仿真运行时间t=100s。

为验证算法对网络长时滞影响下的鲁棒性，改变链路时延R0从20ms到400ms，仿真结果如图2所示，参数统计对比如表1所示。

由图2可见，当网络时延发生变化时，SMPC算法在15s左右调节至期望队列长度150包附近且保持稳定，队列振荡幅度控制在±20%之间，说明SMPC算法对网络时延进行了有效补偿。使用SMC和RED算法的瓶颈链路则在网络时滞影响下出现持续振荡，难以将队列长度稳定在期望值附近。PI算法的队列长度振荡幅度又明显高于SMC和RED算法。由表1的量化指标可知，SMPC在网络长时延的情况下仍然保持较高的链路利用率，同时维持较低的丢包率，其他3种算法在长时延场景下性能损失明显，链路利用率有不同程度的下降。可见当网络系统存在长时延时，SMPC算法的抗干扰能力明显优于其他算法。

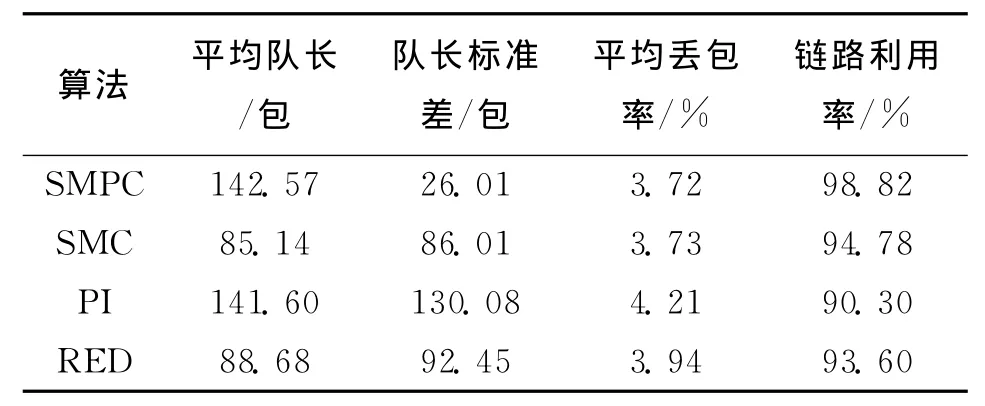
表1 AQM控制算法性能对比

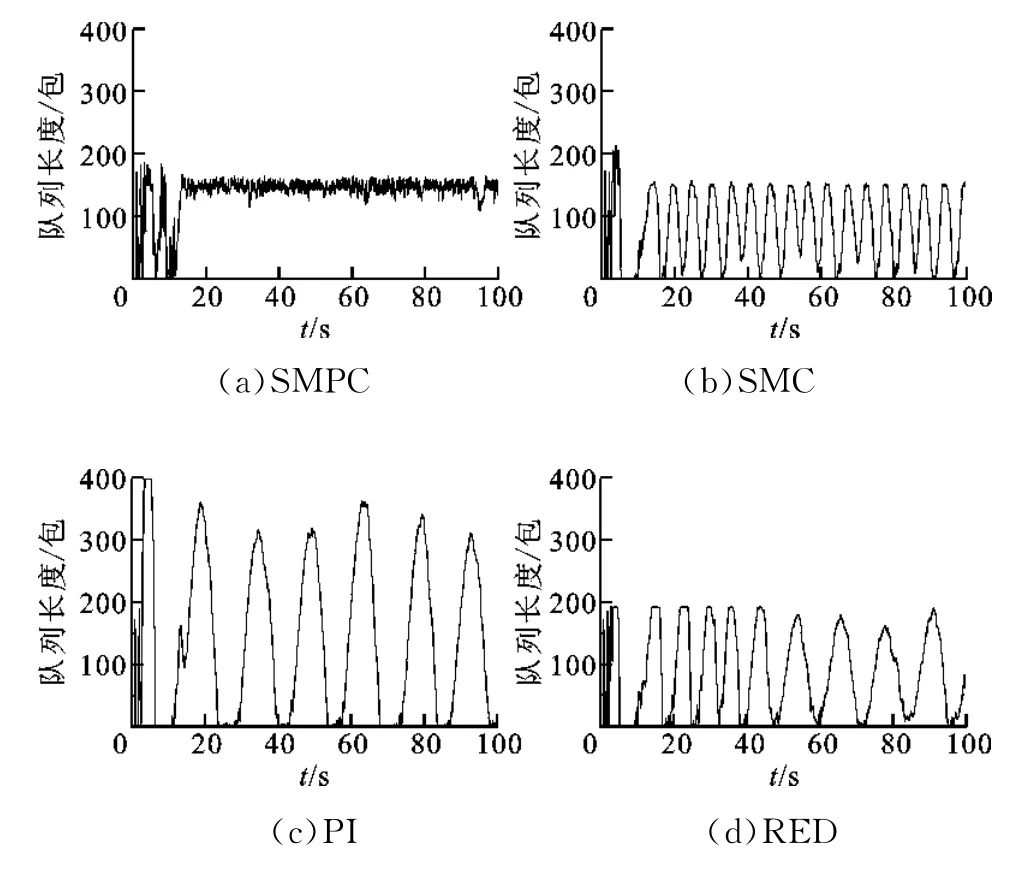
图2 长时延场景AQM控制算法性能比较

4 结 论

本文针对TCP／IP网络模型提出了滑模预测AQM控制策略，利用滑模预测模型来预测网络的未来动态，将滚动优化和反馈校正引入网络拥塞控制中，通过设置预测步长补偿时滞网络不确定时延的影响，优化分组丢包率确保路由队列快速平稳到达目标值，并基于Lyapunov理论给出了当网络中时延发生变化时确保系统渐近稳定的充分条件。仿真对比结果表明，SMPC算法使路由队列波动控制在较小范围内，调节时间短，丢包率较低，综合性能明显优于SMC等算法，克服了往返时延等不确定因素的不利影响，有效避免了网络拥塞发生。

［1］ BRADEN B，CLARK D，CROWCROFT J.Recommendations on queue management and congestion avoidance in the Internet［EB／OL］.（1998-04-01）［2007-06-23］.http：∥www.faqs.org／rfcs／rfc2309，2011.9.

［2］ 安智平，张德运，赵东平，等.一种适用于实时多媒体业务的随机早期检测算法 ［J］.西安交通大学学报，2004，38（10）：1061-1064.

AN Zhiping，ZHANG Deyun，ZHAO Dongping，et al.Real-time enhanced random early detection algorithm for multimedia service［J］.Journal of Xi’an Jiaotong University，2004，38（10）：1061-1064.

［3］ CHEN C K，KUO H H，YAN J J.GA-based PID active queue management control design for a class of TCP communication networks ［J］.Expert Systems with Applications，2009，36（2）：1903-1913.

［4］ 王萍，陈虹，杨晓萍.动态矩阵主动队列管理算法［J］.控制理论与应用，2010，27（8）：971-978.

WANG Ping，CHEN Hong，YANG Xiaoping.Active queue management algorithm with dynamic matrix control［J］.Control Theory and Applications，2010，27（8）：971-978.

［5］ 刘胜，方亮，赵斐.基于SMC的飞机仿真器航道罗盘伺服系统研究 ［J］.计算机工程与应用，2008，44（16）：240-242.

LIU Sheng，FANG Liang，ZHAO Fei.Research on servo system of flight simulator path compass based on sliding mode control［J］.Computer Engineering and Applications，2008，44（16）：240-242.

［6］ 高海燕，蔡远利.高超声速飞行器的滑模预测控制方法 ［J］.西安交通大学学报，2014，48（1）：67-72.

GAO Haiyan，CAI Yuanli.Sliding mode predictive control for hypersonic vehicle ［J］.Journal of Xi’an Jiaotong University，2014，48（1）：67-72.

［7］ 陈炳卿，牛玉刚.网络拥塞控制的滑模控制策略 ［J］.计算机工程与应用，2009，45（26）：94-97.

CHEN Bingqing，NIU Yugang.Network congestion control based on sliding mode control［J］.Computer Engineering and Applications，2009，45（26）：94-97.

［8］ MISRA V，GONG W B，TOWSLEY D.Fluid-based analysis of a network of AQM routers supporting TCP flows with an application to RED ［C］∥Proceedings of the Conference on Applications， Technologies，Architectures， and Protocols for Computers Communication.New York，USA：ACM，2000：151-160.