基于聚类的干扰资源优化分配研究＊

（海军蚌埠士官学校 蚌埠 233012）

1 引言

雷达干扰资源分配是指通过雷达侦察得到敌方雷达的参数，根据我方现有的干扰资源和战术要求，针对敌方雷达的威胁时间和威胁程度，合理分配我方的雷达干扰资源的过程[1]。雷达干扰资源的分配是否合理，己经成为影响作战结果的重要因素之一。在实战中，为了使己方的干扰机能够对敌方的雷达进行最大程度的压制，更好地对我方的人员和装备实施保护，要求对我方的干扰资源进行合理高效的分配。目前来讲，干扰资源分配的主要依据是作战指挥员的经验。但是，如果在复杂的电磁环境下依然依靠这种手动的经验式的分配方式，就有可能造成严重的后果。如何在时间紧迫、高度复杂的现代战场，对我方有限的干扰资源进行合理的分配使其发挥最佳的干扰效果，一直是我们研究的一个重点课题。

FKM（Fuzzy K－Means）是相对于硬聚类（一个样本必须属于也只能属于某一个类）而言的一种聚类方法。在样本聚类过程中产品往往可能属于多个类群，FKM方法通过引入隶属度概念把聚类分析技术和模糊集技术相结合，能够更好地反映样本类型[2]。文中主要是对基于聚类的干扰资源分配方法进行分析和研究，针对现有资源分配方法的不足之处提出了改进方案，该方法对实战中雷达干扰资源的优化分配具有一定的指导意义。最后对雷达侦察和干扰效果进行了仿真实现。

2 雷达干扰资源优化分配模型

在实战中，为了使己方的干扰机能够对敌方的雷达进行最大程度的压制，更好地对我方的人员和装备实施保护，要求对我方的干扰资源进行合理高效的分配。

当多部干扰机对空中目标进行电子战支援时，每部干扰机进入雷达接收端的干扰信号分别为

而雷达目标的回波信号功率为

式中：Pt是雷达发射功率，Gt是雷达在天线主瓣方向增益，σ是雷达目标的有效反射截面积，λ是雷达的工作波长，Rt是雷达到目标的距离，A是雷达天线的有效面积。

干扰信号和目标信号的功率比为

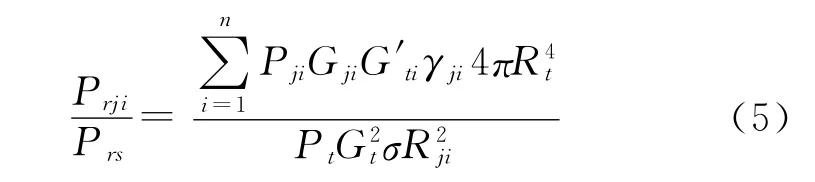
则干扰方程满足：

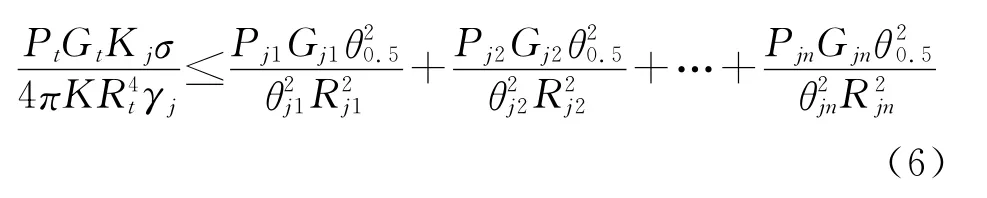
式中：Pj是干扰机发射功率；Gj是干扰机天线主瓣方向增益；θ是雷达信号的主瓣方向和干扰机信号的主瓣方向之间的夹角；Rj是干扰机到雷达的距离；γj是干扰信号对雷达天线的极化损失；Kj是雷达正常工作时所必须的最小干信比。

雷达接收机输入端干扰和信号的功率比为

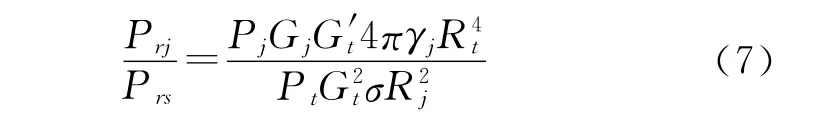
当干扰与信号功率比大于压制雷达对信号正常接收时所必须的干扰与信号的最小功率比Kj时，可得到干扰方程的一般表达式：

仿真及结论：

采用Matlab语言对干扰压制区域进行绘制，将n＝（2，3）分别代入干扰方程进行仿真。

仿真结果如图所示，图1（a）是一部干扰机进行干扰时的干扰区域图，图1（b）是两部干扰机进行干扰时的干扰区域图，图1（c）是三部干扰机进行干扰时的干扰区域图。

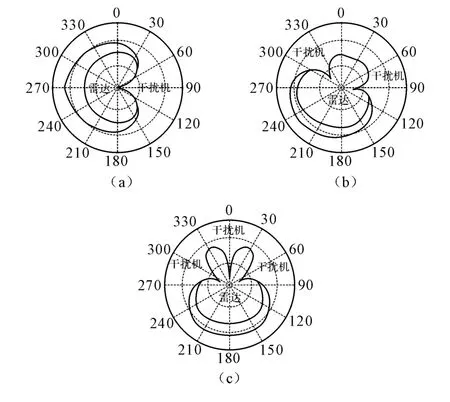
图1 干扰机干扰时区域图

通过对参数θ的调整，可以计算出最小干扰距离随参数θ的变化量，就可以得到支援干扰在多种情况下对雷达探测性能的影响程度。从得到的数据结果，得到结论：

1）在雷达、目标、干扰机三个参数一定的情况下，干扰机对雷达的压制效果明显，使雷达暴露区域减小，对雷达的压制区域增大[3]。

2）使用单部干扰机进行干扰时，天线增益近似公式适用于θ＞θ0.5／2和θ≤60°～90°，在θ＞θ0.5／2时，可以认为G′t／Gt≈1；θ≥60°～90°时，天线平均电平变化范围很小，可以认为不受θ平方的影响而变化。

3）在使用多部干扰机进行干扰时，要取得更好的干扰效果，就要使干扰机对雷达实施干扰时尽可能的对准雷达的主瓣；在雷达、目标和干扰机三个参数一定时，我们要选取每一部干扰机的最佳位置，使得干扰机能够更好地保护被保护目标[4]。这就要求合理地对干扰机资源进行优化分配，以取得最佳效果。

3 基于聚类的干扰效益最大化算法研究

在多部干扰机对多部雷达实施干扰时，要想确定如何分配干扰资源，得到最佳干扰效益，就要对干扰资源分配算法进行进一步的研究[5]，下面是在聚类算法的基础上实现对干扰资源的最优分配。

3.1 优化流程

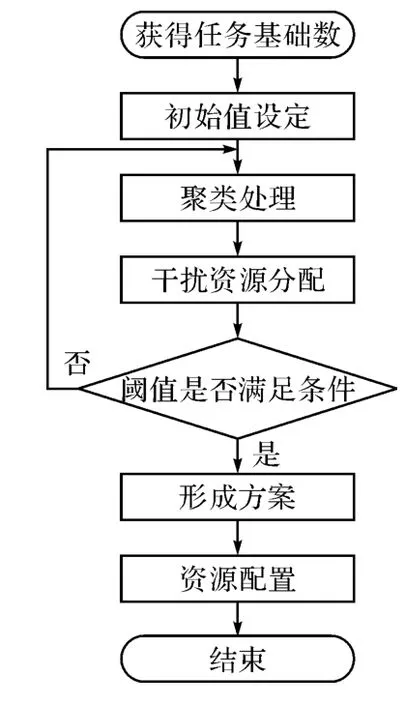
图2 优化流程图

资源配置初期，获得任务相关信息并建立基础数据库。在数据处理阶段，对任务信息进行聚类分解，把特征参数相似度较高的多个任务分配为一个类群[6]，针对不同类群的参数信息得到不同的干扰资源配置方案。根据预先设定的阈值，检查干扰资源的干扰效果，效果不佳的聚类方案进行再次处理，通过对任务信息的重新聚类，获得新的配置方案，并进行再次检查，直到满足阈值条件，把新的配置方案作为资源配置的最优方案。

3.2 基于聚类的资源分配算法

基于贴近度的雷达干扰资源分配策略[7]，该方法是在多级优化动态资源分配算法的基础上对影响雷达干扰效果的时域、空域、频域、能量域、工作体制及对抗样式等方面进行了详细分析，构建了雷达干扰效果的评估指标体系。最后利用Euclid贴近度原理，对干扰资源的分配策略进行进一步的研究。该方法易于计算机实现，本文在此基础上提出了基于FKM聚类的资源分配算法。

我们在解决资源配置的具体问题中，把对方的雷达包括预警机的技术参数作为样本，我方干扰机技术参数作为初始聚类中心，通过聚类算法修正聚类中心，在达到阈值条件下得到优化后的干扰机技术参数[8]。干扰资源分配采用的FKM聚类过程如下：

1）确定聚类模型

｛xi，i＝1，2，…，n｝表示对方组网雷达的样本空间（n为样本个数），｛mj，j＝1，2，…，k｝表示聚类中心（k为聚类中心个数），即我方干扰机配置情况，uj（xi）表示样本i对聚类中心j隶属度，则隶属度约束条件为

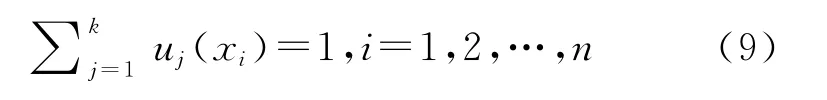
2）构造目标函数

模糊聚类准则函数：

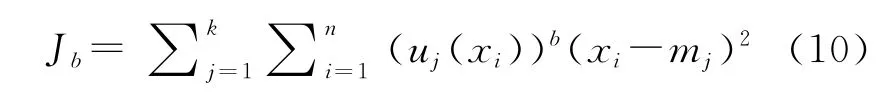
其中模糊指数b＞1，b越大聚类的模糊程度就越大，经有效性实验其取值最佳区间为[1.5，2.5]。根据样本与聚类中心距离最短原则构造目标函数：

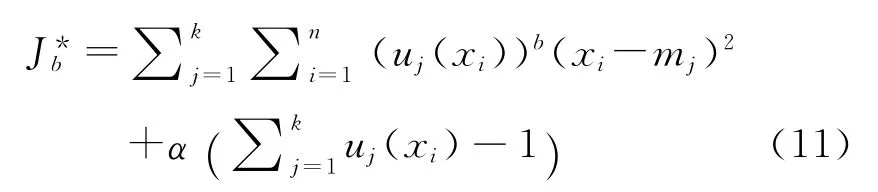
α为拉格朗日算子。

根据隶属度约束对目标函数求偏微分可得极值条件：

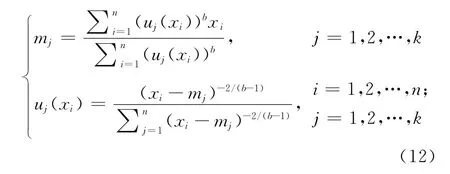
3）聚类迭代运算

步骤一：人为决定k个聚类中心；

步骤二：运用极值条件；

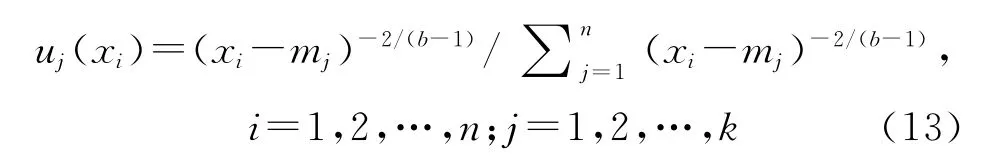
计算样本i对聚类中心j的隶属度；

步骤三：运用极值条件；

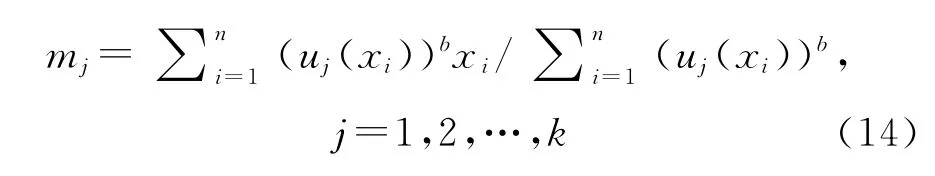
把步骤二计算的隶属度代入式（14），得到新的聚类中心；

步骤四：判断隶属度，如果变化则返回步骤二，如果不变化则终止。

4 基于聚类的资源分配算法应用

为了直观介绍资源分配算法聚类过程，下面模拟多目标雷达任务干扰资源案例简述实现过程。表1为对方组网雷达的样本数据。

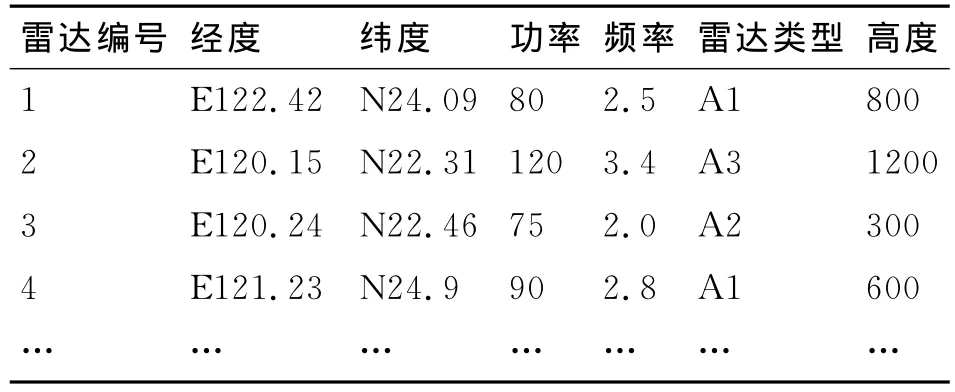
表1 对方组网雷达的相关数据

通过观察分析，对方组网雷达的相关数据不但和经度、纬度、功率相联系，而且还与雷达类型、高度有关。其中经度、纬度、功率、频率为数字形式描述，雷达类型为文字形式描述，同类雷达往往在技术参数上比较接近。由此可以初步制定组网雷达聚类方案：步骤一，以雷达类型进行第一次样本分类，找出同类型的雷达。步骤二，以同类型的多部雷达为样本，经度、纬度、功率、频率等相关信息的记录为参数，进行聚类。

设定聚类条件：雷达类型＝A1，对当前雷达样本进行分类，得到符合条件的雷达样本空间。

表2 聚类样本空间

4.1 对样本空间进行层次（AHP）聚类[9]

1）设定初始值

类群数k等于表2中样本个数，对样本的经度、纬度、功率、频率等参数进行归一化处理，初始化阈值系数λ为1／10。

2）迭代合并

遍历所有类群，计算各个类群间距离：

其中xi1、xi2、xi3、xj1、xj2、xj3分别代表xi和xj的经度、纬度和功率。计算阈值α1＝dmin＋λ（dmaxdmin），α2＝dmax／（k－1），遍历比较dij和α1和α2，

直至所有样本比较结束，完成本次遍历，重复2）直到所有类群都不满足dij＜α1或dij＜α2，则终止合并。

4.2 对样本空间进行FKM聚类

1）设定初始值

聚类中心个数k和聚类中心m；由层次聚类结果决定。设置模糊系数b＝2，则隶属度函数可以表示为（样本个数为n）：

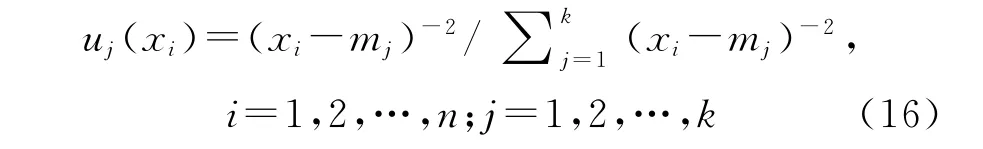
聚类中心函数可表示为

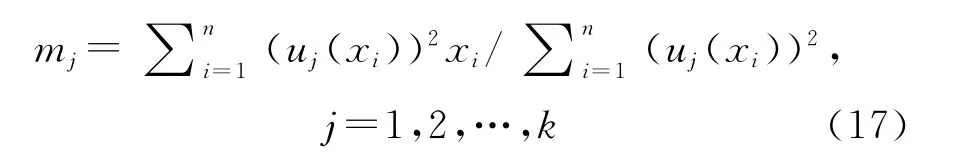
2）循环聚类

根据隶属度函数遍历计算隶属度uj（xi），并依据隶属度按照聚类中心函数计算新的聚类中心mj。判断隶属度，如果变化则返回循环计算，如果不变化则终止[10]。

通过上述两次聚类的过程可以找到经度、纬度、功率、频率最类似的类群：

表3 当前样本聚类结果信息

4.3 仿真结果比较

通常同一类群的技术参数都很相似，对干扰资源配置有很强的指导性。采用聚类分群思想，综合考虑了对方组网雷达的样本空间的时域、频域及空间信息，不断修正我方干扰机配置参数，精度和速度都达到了设计要求。仿真比较结果如图3所示。

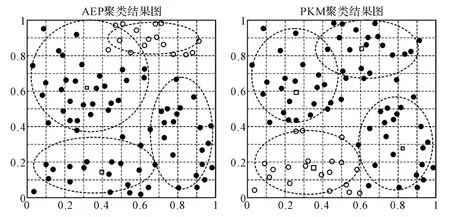
图3 AHP与FKM算法的聚类结果比较

图3上方部分所示为基于AHP的聚类结果，其中类群划分的重复区域较大，该区域通常具有较大争议，对类群中心的偏差具有较大影响；图3下方部分所示为基于FKM算法的聚类结果，可以明显看到该图中的重复区域很大程度上得到修正，各类群的分布也相对均匀。通过上述验证比较可知，AHP和FKM两种方法的分类精度确实存在一定差异，但是聚类中心的位置大致类似，可以作为相互检验的依据。

AHP与FKM比较而言，前者分类结果的准确度不尽如人意，后者虽然在运算速度上存在一定不足，但是弥补了准确度的问题。采用AHP－FKM混合的方法可以同时弥补这两种算法的不足。图4所示Matlab分类信息即FKM算法和AHPFKM混合算法的聚类结果比较：左右图示两种聚类方法得到的聚类中心位置和类群划分完全吻合。但是从目标函数的变化曲线可以明显看出两种方法在回归速度上的较大差异，左图目标函数在循环10次左右趋于稳定，右图目标函数在循环3次左右就已经趋于稳定。在运行过程中设置跟踪节点，可以很快跟踪到前者循环59次终止运算，后者循环73次终止运算。通过实现图示可以直观的看出，AHP－FKM混合算法比单纯的AHP算法具有更高的精度，相对单纯的FKM算法又具有速度上的极大优势。

图4 FKM与AHP－FKM混合算法分类结果比较

5 结语

本文研究了现代电子战背景中雷达干扰资源的优化分配问题，给出了雷达干扰资源的优化分配算法，通过计算机仿真说明了算法的实用性。但是，由于目标雷达的位置不同、时间不同，因此其任务权重也在发生变化。这就要根据任务的变化和需要及时考虑并调整干扰资源的分配，以使得在每一阶段都能得到最佳的整体干扰效果。这样才能使得战场仿真更加贴近实战效果，从而更好地为战场指挥官提供科学的决策依据。

[1]郝晓军，傅仪源，王伟，等.电子对抗中的极化方式选择[J].电子信息对抗技术，2007（4）：32－36.

[2]姜宁，等.雷达干扰资源分配的模糊多属性动态规划模型[J].南京理工大学学报，2003（6）：41－43.

[3]李朝健，肖建华.常用聚类算法比较分析[J].电脑知识与技术，2007（2）：11－14.

[4]黄贤锋，张万军，等.雷达干扰智能决策资源分配的一种快速算法[J].航天电子对抗，2002（6）：20－22.

[5]郭小一.多策略雷达干扰资源分配方法研究[D].长沙：国防科技大学，2006.

[6]谈江海，陈天麒.一种雷达干扰资源分配算法[J].电子对抗技术，2005（5）：11－13.

[7]吕永胜，王树宗，等.基于贴近度的雷达干扰资源分配策略研究[J].系统工程与电子技术，2005（11）：22－25.

[8]杨占华，杨燕.一种基于SOM和K－Means的文档聚类算法[J].计算机应用研究，2006（5）：15－18.

[9]黄志红.基于层次聚类的k均值算法研究[J].电脑开发与应用，2009（7）：22－25.

[10]顾洪博，张继怀.聚类算法初始聚类中心的优化[J].西安工程大学学报，2010（2）：13－15.