防空导弹对直杆型杀伤模型单发杀伤概率计算＊

（海军航空工程学院 烟台 264001）

1 引言

由于不同目标的要害分布以及性质差别很大，所以在计算战斗部条件杀伤概率时，要对目标的要害分布类型做出假设。通常的假设方法有两种：一是要害舱段杀伤模型，这是针对给定具体尺寸、位置、性质的目标时使用的模型；二是直杆型杀伤模型，它将目标假设为由多条等效直杆组成，便于在不对特定的目标结构进行详细分析时使用。本文探究的是利用概率密度积分法，提出了在针对直杆型杀伤模型时，防空导弹对其单发杀伤概率的计算方法。

2 单发杀伤概率一般表达式

[1]，防空导弹的单发杀伤概率在由脱靶量ρ，脱靶方位角θ以及xr轴构成的圆柱坐标系中可以写为

式中Pf（ρ，θ）是脱靶条件为ρ，θ下，引信的启动概率；fg（ρ，θ）是制导误差为ρ，θ的二维分布密度函数；ff（xr｜ρ，θ）是引信启动点一维坐标xr分布密度函数。

定义引信战斗部联合条件杀伤概率Pdf（xr｜ρ，θ）为

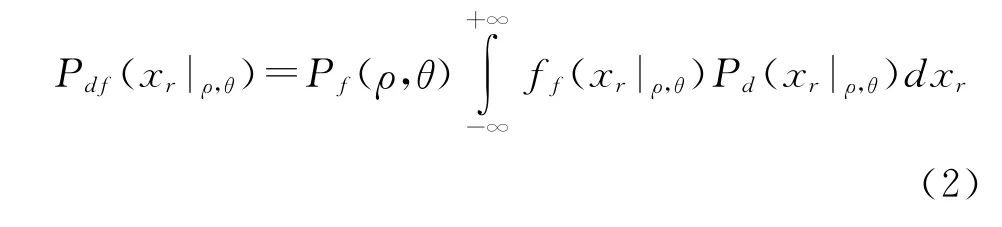
综上所述可得：

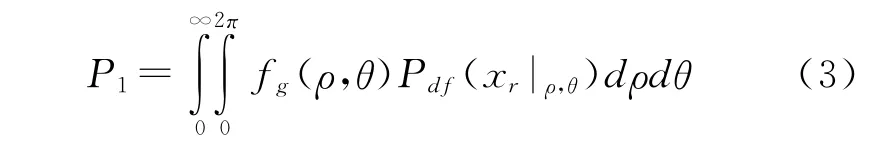
3 单发杀伤概率三维数字积分计算

在进行三位数字积分之前，可先用简化的解析法估算单发杀伤概率值。进行简化解析法计算时，假设目标为单一直杆型模型，在制导脱靶的可能范围内启动概率Pf＝1，同时只考虑战斗部条件杀伤概率，系统误差为0。通过参考文献[1]中的公式，可以估算出：若战斗部特征半径与制导误差的比值不小于4，则可以得到不低于98%的单发杀伤概率。

而在进行三维数字积分时，由于弹目交会情况复杂，首先要将实际脱靶量ρ分成两部分：0～ρ0以及ρ0～ρmax，在0＜ρ＜ρ0时，战斗部的威力足以摧毁目标，其条件杀伤概率为1，因此，可以得到圆柱坐标下的计算单发杀伤概率的公式为

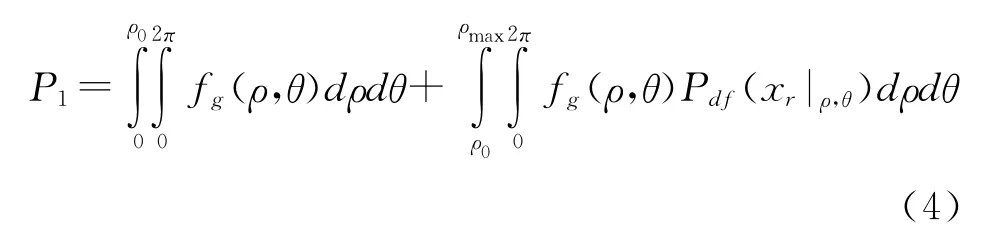
其中制导误差的概率密度函数fg（ρ，θ）的计算式为

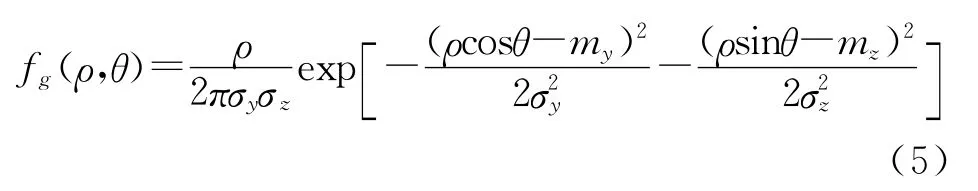
式中的my、mz为脱靶参数中的系统误差，σy、σz为随机误差标准差，两个方向上的误差是相互独立的[1]。

3.1 在给定脱靶圆内的杀伤概率

在脱靶误差服从二维正态分布的条件下，落入给定半径ρ0内的概率可以通过二重积分或蒙特卡洛法对上式求得结果。但是在实际应用中，计算落入定脱靶圆内的概率的情况可以分为圆散布和椭圆散布两种状态，椭圆散布代表着实际弹道的标准差σy≠σz。简便起见，本文假设弹道为圆散布，即σy＝σz＝σ。在这种情况下，设t＝ρ／σ，a＝m／σ，最终落入给定脱靶圆的概率可写成：

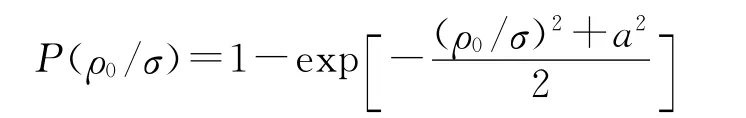
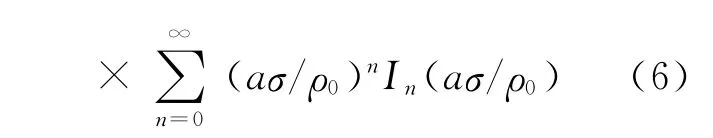
在实际弹道的散布中心与质心相重合的时候，系统误差等于零。在大多数情况下，系统误差可以通过加入校正信号予以消除，对于一个成熟的导弹武器系统而言，都可以认为其系统误差为零，即m＝0，则a＝0，因此零阶虚位移贝塞尔函数I0（aσ／ρ0）＝1，又因为In（aσ／ρ0）＝0，n＞0，则得到最终的落入脱靶圆的概率为[2]

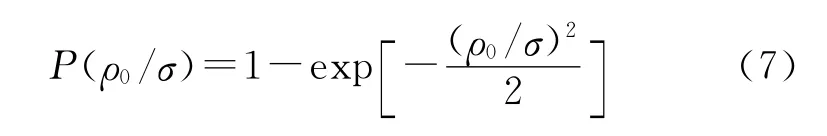
3.2 给定脱靶圆到最大可能脱靶量之间的杀伤概率

3.2.1 直杆型杀伤模型的洞穿概率

在脱靶量ρ大于给定的值ρ0时，就需要计算战斗部的条件杀伤概率。计算时要考虑破片对目标要害部位的杀伤作用以及冲击波对目标的爆破毁伤作用。由于目标要害分布的不同则计算战斗部条件杀伤概率的方法就不同。本文假设目标为直杆杀伤模型，即目标由多条等效直杆组成，每条直杆代表着机体上的重要部件诸如机翼、发动机等。此模型假设当任一根直杆落入战斗部破片的动态飞散带时就认为目标受到一定概率的杀伤，而不单独考虑命中破片数。在这种假设下：

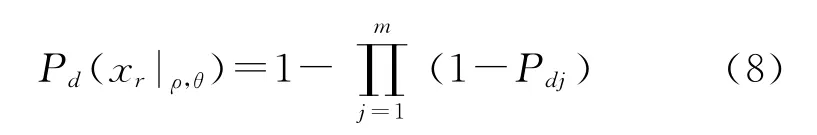
其中，m为目标可杀伤直杆的总数，Pdj为战斗部对第j个直杆的杀伤概率。这里不考虑引燃概率，引爆概率与冲击波毁伤概率，只考虑洞穿杀伤概率。Pdj由Pd1和Pd2两部分组成，Pd1是驾驶舱等重要单个设备舱段的洞穿杀伤概率，Pd2为几个舱段组合杀伤概率，即只有在杀伤全部舱段组合才能杀伤目标。Pd1表达式为

其中，j1是这类舱段的总数，Nj是j舱段命中破片的平均数，P（Ej）是单枚破片对j舱段的洞穿杀伤概率。

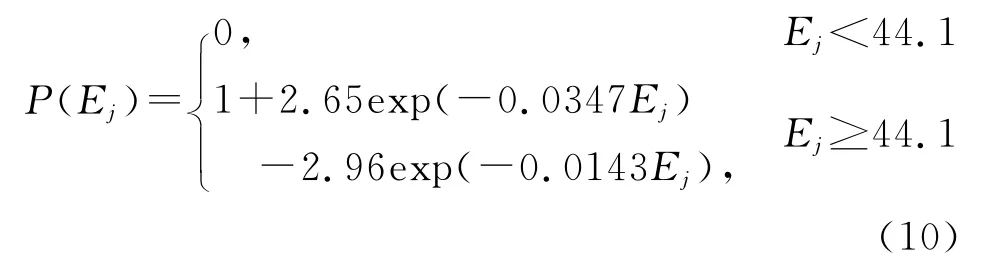
Ej为破片平均比能，即单位破片平均迎风面积上的动能。

3.2.2 要害舱段命中破片数的计算

图1所示为战斗部动态飞散过程中各个矢量的意义以及之间的关系。

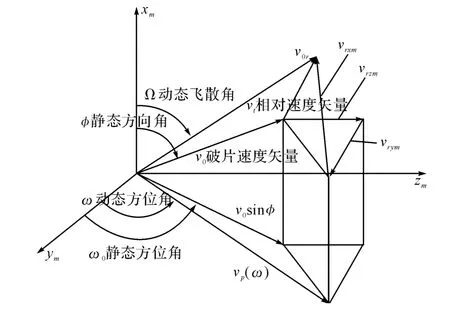
图1 战斗部破片静态、动态飞散角及飞散速度

通过图1中所标注的参数可以求得j舱段命中破片的平均数Nj：

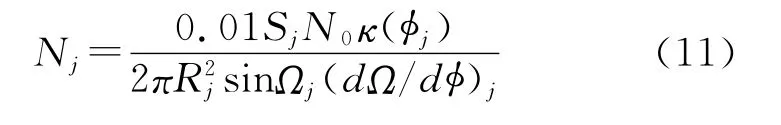
式中已知Ωj、ωj以及第j个要害舱段中心与战斗部中心的连线矢量Rj，于是可以推导出φj和破片飞散密度κ（φj）。Sj是第j个要害舱段在破片动态飞散方向上的等效投影面积。在计算Sj时，根据目标要害不同位置的不同形状，做出如下三种不同的等效几何模型：

1）驾驶舱或油箱等可以等效为球体的要害舱段，其投影面积为常数，即Sj＝const；

2）发动机舱、机身等要害位置，其投影面积为端面与侧面投影面积之和，即Sj＝Sj0｜cosqj｜＋Sj1｜sinqj｜；

3）机翼、尾翼等位置，其投影面积为这些要害位置在Rj上的投影，即Sj＝Sj0｜cosqj｜。

3.2.3 引信启动区

在引信启动区间内，引信战斗部联合条件杀伤概率Pdf（xr｜ρ，θ）变为

Pf（xr｜ρ，θ）是引信的启动概率，在引信启动区范围内，计算式为

在导弹接近目标时，通常近似认为引信启动点沿相对速度坐标系oxm轴的分布服从一维正态分布规律，其分布密度函数为

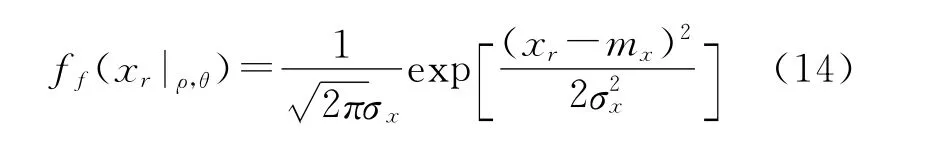
式（14）中的两个未知量，mx是启动点的数学期望，对于光学引信来讲，光学引信视场较窄，mx与引信延迟时间τ以及导弹战斗部中心相对速度坐标系内xr轴上的坐标有关，计算式为

引信启动点的散布σx由四部分的平方和构成：延迟时间散布造成的启动点散布σ1，光学引信主光倾角散布所造成的启动点散布σ2，引信灵敏度变化引起的启动点散布σ3以及目标反射信号起伏所造成的启动点的散布

由以上的分析，可以依次求得在直杆型杀伤模型的情况下的洞穿概率，引信战斗部联合杀伤概率，进而可以求出给定脱靶圆到最大可能脱靶量的杀伤概率，最终得到防空导弹单发杀伤概率的结果。

4 仿真计算

在进行仿真计算时，以某型防空导弹为例，整个计算过程的流程如图2所示。

图2 计算导弹单发杀伤概率的流程

由以上流程，防空导弹使用激光引信，假设该防空导弹破片战斗部的参数为：弹目交会遭遇点高度为22000m，遭遇点斜距为30000m，导弹速度为1000m／s，弹道倾角18°，目标运动速度600m／s，导弹制导系统误差m＝0，随机误差的标准差σ＝4m，战斗部破片数为5000块，破片的初速度为3000m／s，平均每块破片的质量为6g，破片飞散方位角为30°，飞散方向角为60°。

由之前叙述的计算方法，假设模型为直杆型模型，其中1舱段等效为圆柱形，2、3、4、5舱段等效为平板型，计算出每个舱段命中的破片数，其中1舱段命中1000枚，2、3舱段各1500枚，4、5舱段各500枚。目标的模型如图3所示。

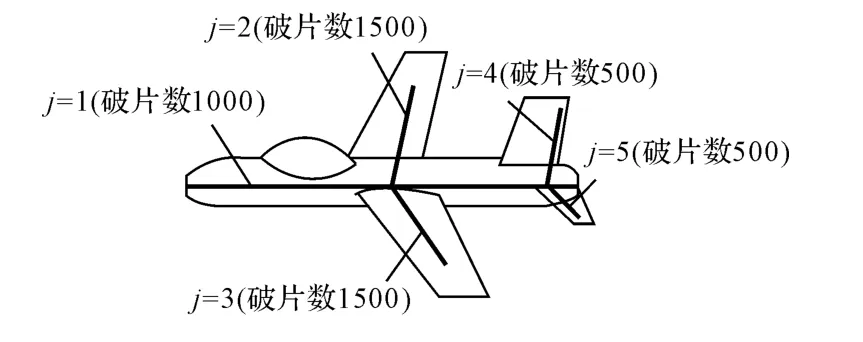
图3 直杆型杀伤模型的目标易损构件

由以上参数可以得出当系统误差为0时单发防空导弹的落入概率随脱靶量ρ0变化的关系，其关系如图4所示。

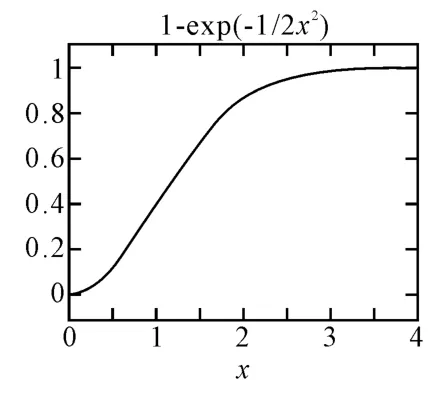
图4 落入概率随脱靶量ρ0的变化曲线

通过前文的论述，当脱靶量ρ0为4m时，由公式：ρmax＝m＋kσ可以得到最大可能脱靶量ρmax为16m。经过计算，在给定脱靶圆内的杀伤概率为39.34%，在给定脱靶圆之外到最大可能脱靶量之间，引信战斗部联合杀伤概率为97.03%，所以杀伤概率为58.80%，两者求和，最终确定该型防空导弹的单发杀伤概率为98.14%，验证了前文当战斗部特征半径与制导误差的比值大于等于4，则单发杀伤概率不低于98%这一估算结果。

5 结语

防空导弹从探测目标到摧毁目标的实际情况十分复杂，实际应用中还需要考虑环境因素，干扰因素等。本文仅选取了落入脱靶圆内的分布为圆分布这一特殊情况进行了计算，并且假设武器系统技术成熟，系统误差等于零，在实际中由于种种因素会导致单发杀伤概率降低。另外，针对不同类型的近炸引信，如无线电引信等，其引信启动区的各种参数的不同会导致单发杀伤概率的不同。在影响单发杀伤概率的诸多因素，例如引战配合效率，战斗部威力，目标易损性等因素。本文针对这些关键因素进行了计算，得到了在该目标类型下，针对激光引信的单发杀伤概率计算方法，在一定程度上可以为武器系统的效能评估提供参考。

参考文献

[1]张志鸿.防空导弹引信与战斗部配合效率和战斗部设计[M].北京：宇航出版社，1994：34－88.

[2]李廷杰.导弹武器系统的效能及其分析[M].北京：国防工业出版社，2000：166－183.

[3]郑平泰，杨涛，王宝敏.拦截弹单发杀伤概率仿真计算研究[J].系统仿真学报，2006，18（7）：1763－1765.

[4]冯融冰，郑世勇，程延杰，等.基于Simulink的防空导弹单发杀伤概率仿真研究[J].舰船电子工程，2011，31（11）：82－84.

[5]王征，李言俊，雷蕾.破片型空空弹杀伤概率三维建模与仿真[J].系统仿真学报，2009，21（17）：5340－5344.

[6]王淼，宋晗，张丽群.防空导弹单发杀伤概率仿真计算研究[J].战术导弹技术，2009（4）：93－96.

[7]孙刚，廖瑛.引战系统数学仿真中战斗部仿真的初步实现[J].上海航天，2006（5）：50－54.

[8]王树林，段江红，杨争，等.用破片覆盖度进行毁伤概率评估[J].现代防御技术，2008，36（1）：36－40.

[9]高波，邱立军，姚跃廷.防空导弹单发杀伤概率研究[J].弹道学报，2011，23（4）：52－55.

[10]王润平，王正向.地空导弹单发杀伤概率之解析算法[J].系统工程与电子技术，2001，23（5）：39－40.