利用线阵实现两点源诱偏仿真试验方法研究＊

（中国洛阳电子装备试验中心 洛阳 471003）

1 引言

随着反辐射武器对雷达的威胁越来越大，如何抗反辐射武器的研究引起了世界各国重视。两点源诱偏具有布站简单、时序控制简单以及所需设备量小等优点，依然是雷达对抗反辐射武器的重要的手段之一。利用射频仿真试验系统进行反辐射武器抗诱偏动态仿真试验，是鉴定和评估其抗有源诱偏干扰能力的一个重要试验手段。为了实现这一目的，一般采用球面阵或线阵模拟反辐射武器在攻击过程中与各个辐射源之间的空间角度变化过程。球面阵模拟时，能够同时实现方位角和俯仰角的变化过程，但是球面阵需要较多的辐射馈源，控制电路复杂，建设周期长。而线阵要求的辐射馈源数目较少，减小了控制的复杂程度，具有投资少见效快的优点。但是线阵自身无法实现方位角和俯仰角同时变化的过程。而这一要求对于检验反辐射武器抗两点源诱偏能力的考核尤其重要。因此本文解决的问题是在内场不具备球面阵的情况下，利用线阵以及三轴仿真转台实现反辐射武器抗两点源诱偏能力的鉴定和评估。

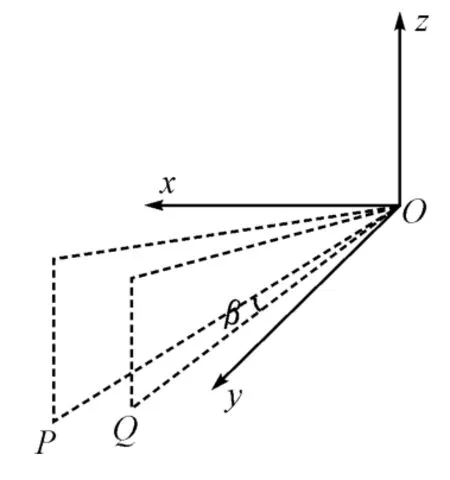
图1 两点源对抗反辐射武器态势图

图1是两点源对抗反辐射武器一般态势图，其中P点为雷达，Q点为诱饵。从图1中可以看出，在反辐射武器攻击过程中，雷达和诱饵相对于反辐射武器在方位角和俯仰角上都有变化量的。由于线天线阵各个辐射馈源与仿真转台的回转中心位于同一水平面上，因此线阵只能模拟出辐射源与反辐射武器之间的方位角的变化过程，而无法同时模拟出反辐射武器攻击过程中的俯仰角的变化过程。但是可以利用线阵模拟出反辐射武器攻击过程中雷达和诱饵之间的夹角β变化过程。本文提出通过修正三轴仿真转台各轴指向以改变反辐射武器姿态的方法，从而确保在仿真过程中雷达和诱饵相对于反辐射武器的角度变化与实际情况相一致。

2 实现原理

2.1 用到的坐标系

1）暗室坐标系

对于射频仿真试验系统，天线阵列辐射单元的安装位置都是基于暗室坐标系标定的，反辐射武器、雷达和诱饵的空间位置关系最终也是在暗室坐标系下确定。

暗室坐标系的坐标原点位于三轴仿真转台回转中心，并与线阵圆心重合。x轴与三轴仿真转台归零后的横滚轴重合，并指向天线阵列；z轴与转台的方位轴重合，y轴与转台的俯仰轴重合。在暗室坐标系下线阵各辐射点的角位置为

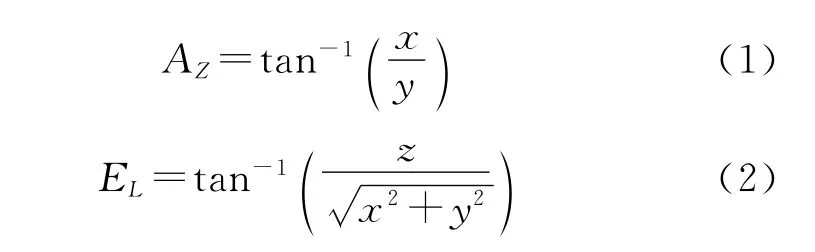
2）发射点惯性坐标系

发射点惯性坐标系原点为发射点，轴铅垂向上，位于水平面内，其指向按需选取，这里取反辐射武器发射时的轴线指向为轴。对于反辐射武器可以不计地球自转，此坐标系与地球固连。

3）弹上坐标系

弹上坐标系的原点位于反辐射武器的质心，而各个坐标轴始终平行于发射点坐标系的轴。在仿真试验中，反辐射武器安装在三轴仿真转台上，弹上坐标系与转台各轴固连在一起。

利用线阵进行两点源诱偏试验时，需要将弹上坐标系中反辐射武器、雷达和诱饵之间的空间关系转换到暗室坐标系下，这一转换通过改变三轴仿真转台各轴的指向实现。但是需要计算三轴仿真转台各轴的转动角度，即转台各轴角度修正值。

2.2 坐标变换

直角坐标系下的坐标变化可以用两种方法实现，一种依次围绕坐标系中的x、y和z轴旋转实现，该方法需要确定三个坐标轴旋转顺序以及各自的旋转角度，这种坐标旋转能够直观反映反辐射武器弹上坐标系变换到暗室坐标系时转台方位轴、俯仰轴和横滚轴的角度修正值φ、φ、θ，但是计算复杂；另一种是围绕任意一轴旋转实现，这种方法称为四元数法，该方法通过定义一个四元数q实现两个坐标系之间绕任意一轴¯E旋转一α角的变换。这两种变换都能够表示两个坐标系之间的变换关系，因此可以通过四元数法确定三轴转台的角度修正值，分别为

3 实现方法

图2为两点源诱偏试验中雷达、诱饵和反辐射武器之间的空间关系。其中反辐射武器位于坐标原点，雷达位于P（xP，yP，zP），诱饵位于Q（xQ，yQ，zQ），线天线阵的辐射源位于半径为R的球面上。

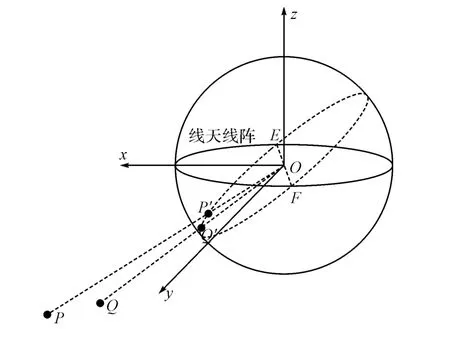
图2 两点源诱偏试验中空间关系

将P、Q两点投影到球面上，可以得到投影点P′（xP′，yP′，zP′）、Q′（xQ′，yQ′，zQ′）的坐标：

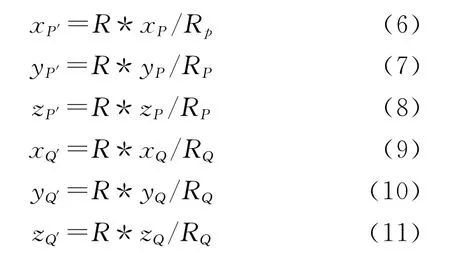
通过P、Q两点的圆与线天线阵所在的圆相交于点E、F，两点的连线通过原点O。相交线EF为

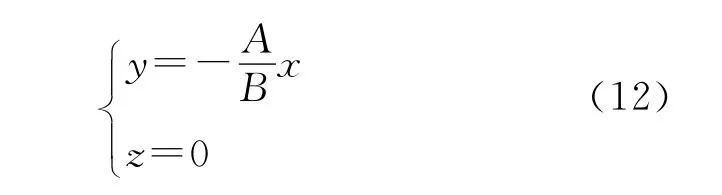
同时两个圆面之间的夹角为

其中A＝yP′zQ′－zP′yQ′、B＝zP′xQ′－xP′zQ′、C＝xP′yQ′－yP′xQ′。

从图2中可以看出P′、Q′所在的圆绕相交线EF旋转α角就能将P′、Q′两点变换到线阵上。

4 仿真验证

假设雷达位于P（26400，1400，－5000），诱饵坐标为Q（26000，1600，－5000），反辐射武器初始位置为M（23658，656，－936.65）。反辐射武器初始状态为水平飞行，到达预定位置后，瞄准雷达与诱饵的中间位置向下攻击。当反辐射武器能够分辨出两个目标后，以最大加速度12m／s2飞向诱饵，并最终击中诱饵。其攻击路线仿真如图3所示。

图3 反辐射武器攻击轨迹

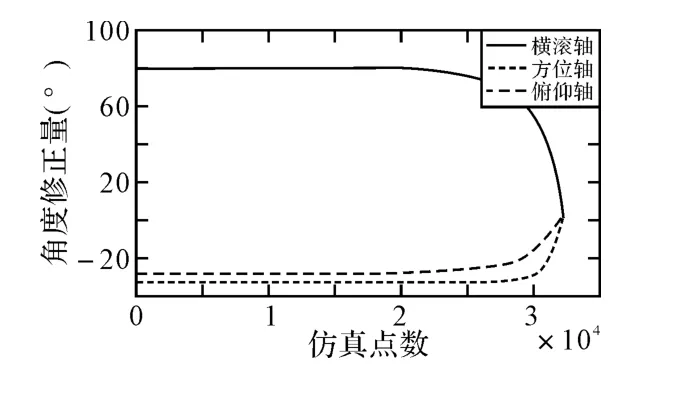
图4 三轴仿真转台各轴修正量

图5 相邻两个仿真周期各轴修正量变化值

利用上述仿真模型计算了三轴仿真转台各轴在整个攻击过程中的角度修正值，其结果如图4所示。仿真计算时以1ms为仿真步进。同时也计算了相邻两个仿真周期（1ms）三轴修正量变化最大值，即角度修正率，分别为0.0368°／ms、0.0246°／ms、0.0088°／ms，这一结果表明说明三轴仿真转台横滚轴、方位轴、俯仰轴的角度修正值变化比较平缓。

5 结语

影响三轴仿真转台的角度的修正量的因素很多，这里仅仅计算了反辐射武器一种典型攻击过程。从仿真结果中可以看出虽然增加了转台在每一个仿真周期内角度变化量，但是考虑到目前仿真转台最大角速度可以达到1000°／s～2000°／s，即在每个仿真周期（1ms）内可以旋转角度1°～2°，而上述角度修正量仅占3.68%左右，因此可以认为对转台仿真能力的影响较小，能够满足仿真试验的需求。

[1]王朝轰，王强，邵友权.非相关两点源诱偏反辐射导弹效果分析[J].海军航空工程学院学报，2007，25（6）：629－632.

[2]杨正，薛业飞，曹志耀.两点源诱骗反辐射导弹的效能评估模型研究[J].电光与控制，2007，14（3）：19－21.

[3]司锡才，查玉峰.两点源抗反辐射导弹诱偏（骗）技术[J].航空学报，1989（6）：13－15.

[4]杨波，罗玉文.两点源诱偏反辐射导弹技术研究[J].空军雷达学院学报，1999（4）：44－47.

[5]李一兵，吴海训，任大孟.抗反辐射导弹雷达诱饵合成场技术的研究[J].信息技术，2003，27（12）：75－76.

[6]吕彤光，姜文利，李盾，等.两点源诱偏被动雷达导引头性能分析[J].系统工程与电子技术，2002（4）：47－50，66.

[7]吕彤光，周一宇，李盾，等.两点源干扰下被动雷达导引头测角性能分析[J].宇航学报，2001（6）：15－25.

[8]戴幻尧.反辐射无人机毁伤辐射源仿真分析[J].电子信息对抗技术，2006，21（3）：38－41，48.

[9]吕彤光，姜文利，李盾，等.两点源干扰情况下数据积累点数对雷达测角精度的影响[J].国防科技大学学报，2001（5）：48－53.

[10]钟志通，王峰，尤祖国.抗击反辐射导弹武器的指挥策略研究[J].战术导弹技术，2003（4）：26－30.

[11]林欢，李青山，甘德云，等.非相参多点源抗反辐射武器诱偏效果半实物辐射式仿真研究[J].舰船电子对抗，2010，33（4）：28－32.

[12]段晓超.诱饵时序控制的实现[J].现代电子，2002（1）：26－28.