带形状调整参数的二次B样条曲线(Ⅱ)

王晶昕,郭丽霞,张嘉洋

(辽宁师范大学 数学学院,辽宁 大连 116029)

0 引言

曲线的生成以及形状调整是计算机辅助几何设计领域一个重要课题.有理Bézier曲线以及有理B样条曲线就是为了这一目的通过将基函数变为带有权因子的有理多项式(分片有理多项式)的方法来实现的(参见文[1]).但这种方法存在一些弱点,譬如计算复杂、权因子的几何意义不直观等.

我们的研究是从另一个角度入手的,即仍使用众所周知的Bernstein基函数、B样条基函数,但通过带形状调整参数的控制点变换矩阵生成一组与原来给定的控制点相关联的新控制点,进而生成相应的曲线曲面,以达到调整曲线曲面形状的目的.

本文是文[2]研究工作的继续,该研究的重要性在于基函数未改变,使得调整后曲线的几何性质可根据控制点的位置及已知基函数的性质来确定.且其中的参数与控制点位置相对应,几何意义明确.

1 带形状调整参数的二次B样条曲线的构造

1.1 曲线构造及性质

利用二次B样条基函数,可以构造二次B样条函数

其中Ni,2(u)诸为二次B样条基函数,诸yi是预先给定的实数,诸Pi是给定的R2或R3中的控制顶点.

称曲线

为带形状调整参数的二次B样条曲线,其中参数αi∈R(i=1,2,…,n)．

文[2]讨论了带参数的二次均匀B样条曲线在曲线端点处如何依控制点参数改变曲线形状的问题,本文是讨论二次均匀B样条曲线内部形状的改变问题.由于B样条曲线特点是局部调整,因此,不失一般性,我们集中讨论在曲线内部涉及七个控制顶点情形之下的曲线形状调整问题.

设Pi(i=0，1，2，…6)是给定的七个控制顶点

则得带α1，α2参数的曲线

其中参数αi∈R(i=1,2)，

通过上述矩阵变换可知产生新控制点比原来控制点多增加一个,调整后曲线比原来曲线多增加一段,通过改变参数大小,调整后曲线只在[3,7]上发生改变.当参数α1∈(0，1)时,点Q3在线段P2P3上,当参数α1∈(1，+∞)时,点Q3在线段P2P3延长线上,当参数α1∈(-∞，0)时,点Q3在线段P2P3反向延长线上.同理,点Q4在P3P4上也有这三种位置关系,因此,根据参数α1，α2的取值范围,调整后控制点有九种类型,图1-4为其中四种类型的例子,其中实线为原来的曲线,虚线为变形后的曲线,并有如下结论:

(1)当参数α1固定在(0，1)内,随着参数α2从0逐渐向1增大或(减小)时,曲线逐渐远离(靠近)线段P2P3,靠近(远离)点P4.

(2)当参数α1固定在(0，1)内,参数α2在(-∞，0)变化时,曲线会增加拐点.

(3)当参数α1固定在(1，+∞)，(-∞，0)变化时,参数α2在(-∞，0)，(1，+∞)变化时,新控制点Q3，Q4，Q5生成的控制折线近似于其相应的曲线形状.当参数α1=1时,曲线经过点P3,由于在该点处一阶导数为零,故其为一尖点.

同样α2固定,改变α1,讨论方法与上述亦然.

此外,当我们让两个参数同时增大同时减小或者一个增大一个减小时,可以更加灵活的实现曲线调整.

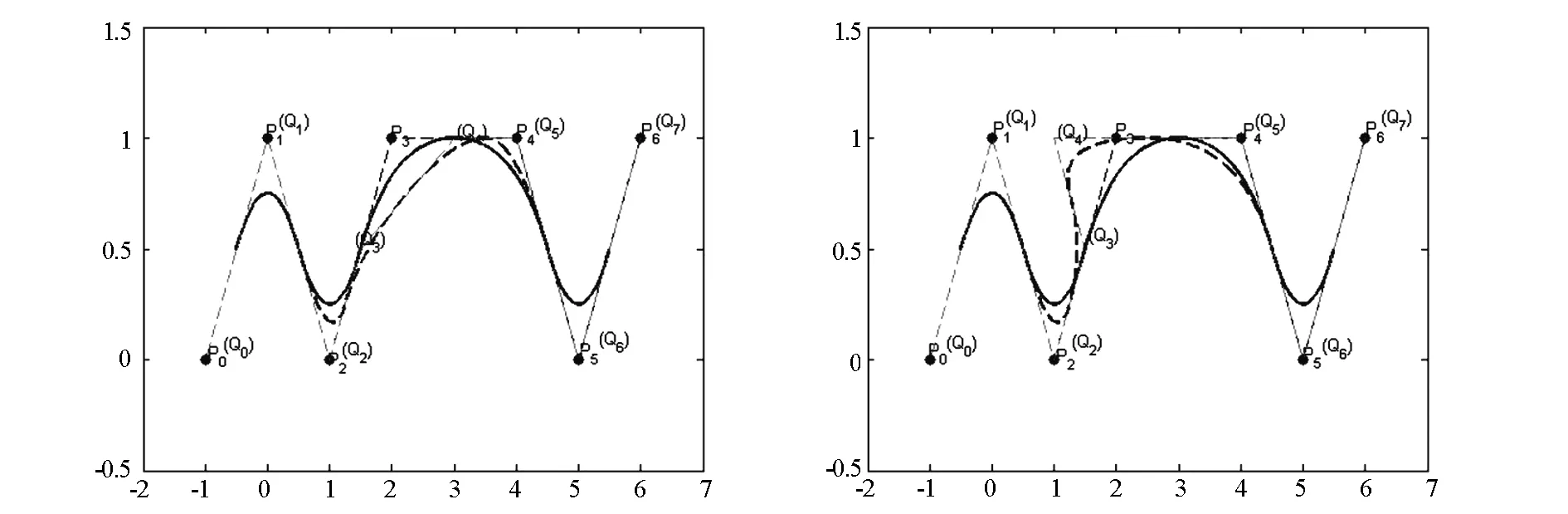
图1α1∈(0，1)，α2∈(0，1)时的二次B样条曲线图2α1∈(0，1)，α2∈(-∞，0)时的二次B样条曲线

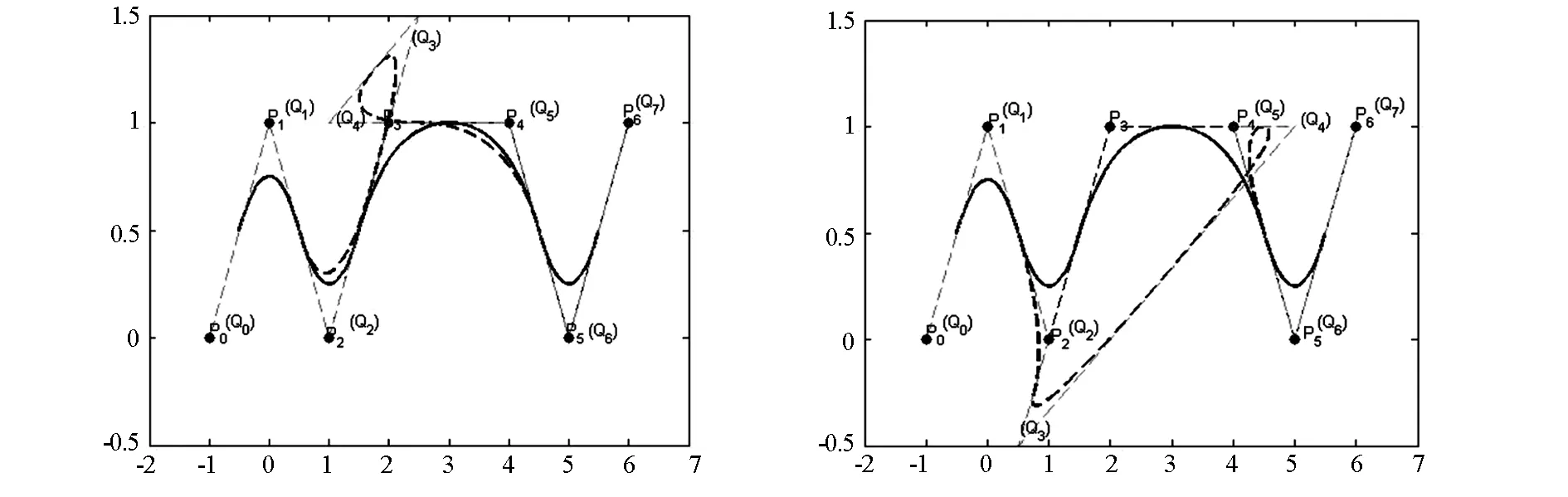
图3α1∈(1,+∞)，α2∈(-∞，0)时的二次B样条曲线图4α1∈(-∞,0)，α2∈(1,+∞)时的二次B样条曲线

1.2 带参数曲线的连续性

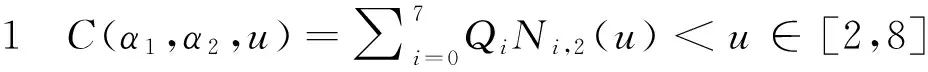
证明:

考虑C(α1，α2,u)任意两段相邻曲线段

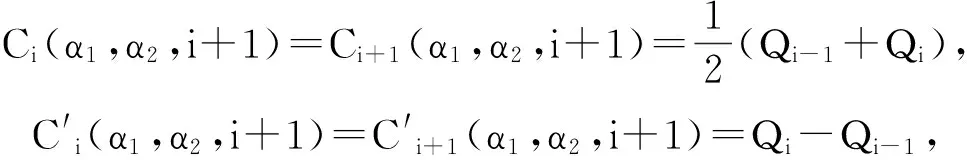
其中i=2,3,…6．

故C(α1,α2,u)是C2连续的.

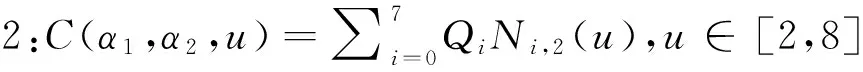
调整参数α1,α2,可使该曲线中G2连续及C2连续.

证明:

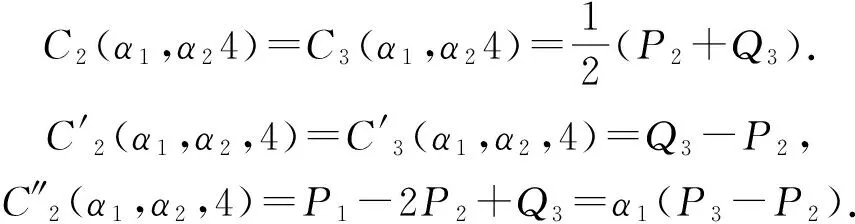
当α2=0时,有Q4=P3从而有

当参数α1∈(0，1/2)时,

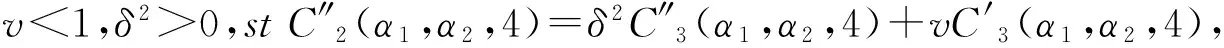
当参数α1∈(-∞,0)或α1∈(1/2，+∞)时,

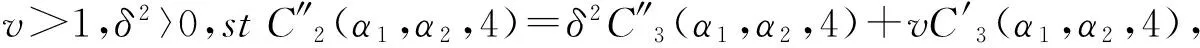
从而曲线中G2连续.

2 曲线的升阶

前面给出的曲线C(α1,α2,u)仍是二次B样条曲线,注意到生成的新控制顶点比原来的控制顶点多一个,因此,还可以用这种新的控制点生成一条三次B样条曲线

其中Ni,3(u)为三次均匀B样条基函数.

仍利用前面所取的参数,生成的三次均匀B样条曲线如图5-8所示,就此可以看出它们与相对应的二次均匀B样条曲线的差别.其中实线为新生成的二次均匀B样条曲线,虚线为新生成的三次均匀B样条曲线.

针对于参数α1,α2而言,当它们取值相同时,新生成的二次B样条曲线整体逼近控制多边形的速度比新产生三次B样条曲线要快,但新产生三次B样条曲线光滑性比二次B样条曲线要强.

当α1不变,α2变大或变小,曲线段会相应靠近点P4或P3.同理,当α2不变,α1变大或变小,曲线段会相应靠近点P3或P2.

显然,参数α1,α2所起的作用不同,可根据实际需要作整体或局部调控.

图5α1∈(0，1)，α2∈(0，1)时的三次B样条曲线图6α1∈(0，1)，α2∈(-∞，0)时的三次B样条曲线

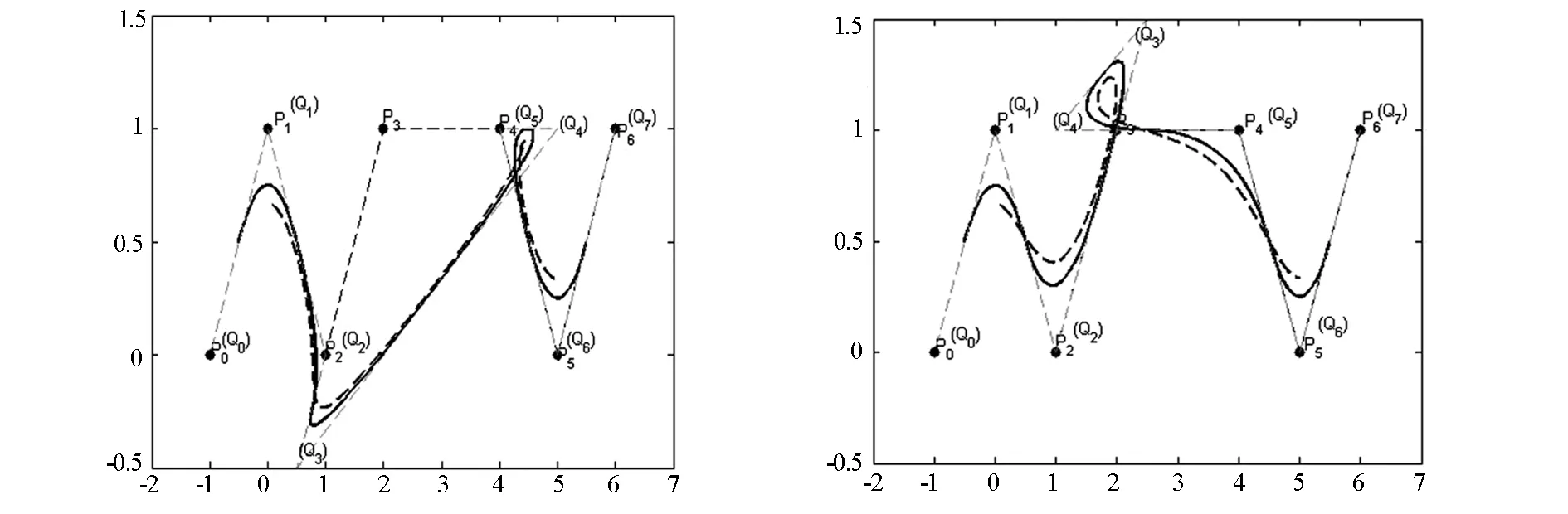
图7α1∈(-∞，0)，α2∈(1，+∞)时的三次B样条曲线图8α1∈(1，+∞)，α2∈(-∞，0)时的三次B样条曲线

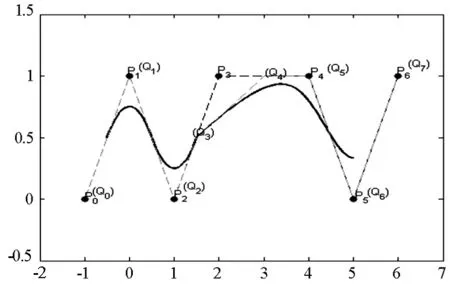
图9 α1=1/2,α2=1/2时的B样条插值曲线

注意到以上构造的带参数的B样条曲线所采用的基函数次数是一样的,同样,我们既可以采用二次均匀B样条基函数以及三次均匀B样条基函数来同时构造带形状调整参数曲线.不失一般性,我们仍用上述生成的八个控制顶点,为了将两段不同次均匀B样条曲线进行拼接,我们在两段曲线公共连接点Q3处需要采用B样条曲线重节点的性质,从而使两段曲线都插值于该点.下面我们主要给出带调整参数曲线在公共连接点处构造形式,并对该点处的连续性进行讨论.

其中N1，2(u)为二次均匀B样条基函数,N1，3(u)为三次均匀B样条基函数.

我们同样可以给参数α1,α2取不同的值得到不同的调整曲线.图9是当α1=1/2，α2=1/2调整后的曲线.

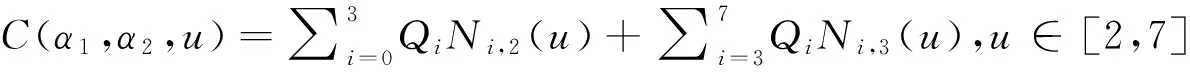
证明:

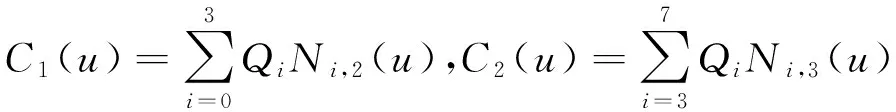
经计算得

C1(4)=Q3,C2(5)=Q3,

=3[(α1-1)P2+(1-α1-α2)P3+α2P4]

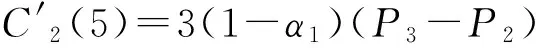
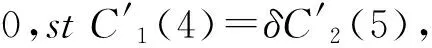
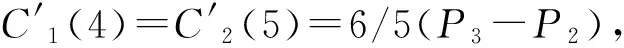
图10-11分别为α1=1/5，α2=0，α1=3/5，α2=0时调整后所得到的曲线.

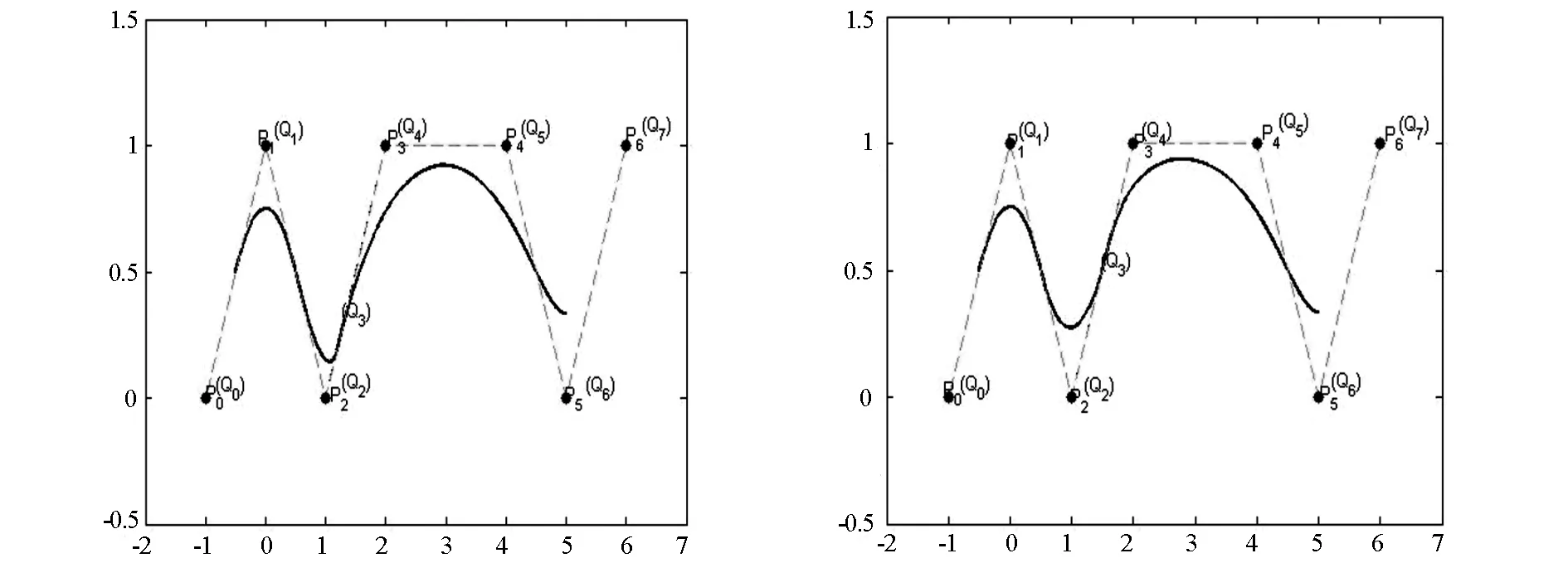
图10α1=1/5,α2=0时的B样条插值曲线图11α1=3/5,α2=0时的B样条插值曲线

3 结论

注意到以上讨论都是针对涉及控制顶点P0，P1，P2，P3，P4，P5，P6情形的.如求曲线的形变时涉及更多的控制点,依照同样的原理可以生成关于更多参数的B条曲线.而且随着基函数类型变化增多,可以利用本文给出带参数变换矩阵生成一组新控制点的方法,构造相应的带参数的曲线,进而完成曲线形状调整任务.

[1]Farin G.Curves and surfaces for computer aided geometric design[M].New York:Academic Press,1988.

[2]王晶昕, 闫惠蔷. 带形状调整参数的二次B 样条曲线(I)[J]. 吉林师范大学学报(自然科学版),2011,32(4):5～7.

[3]王仁宏. 数值逼近[M].北京:高等教育出版社,1999.

[4]王晶昕,牛 鑫.椭圆曲线的带调节参数的Bézier曲线逼近[J]. 吉林师范大学学报(自然科学版), 2011, 32(1)：8～10.

[5]刘长明, 檀结庆. 二次均匀B样条曲线的扩展[J]. 合肥工业大学学报(自然科学版), 2004, 27(5): 459～463.

[6]廖丽君, 肖鸣宇. 二次均匀B样条方法的扩展与应用[J]. 曲阜师范大学学报, 2005, 31(4):114～118.

[7]韩旭里, 刘圣军. 三次均匀B样条曲线的扩展[J]. 计算机辅助设计与图形学学报, 2003,15(5):576～578.

[8]熊 建. 带多形状参数的样条曲线曲面及其应用研究[D]. 合肥工业大学, 2008.

[9]谢 进, 洪素珍. 带形状参数的二次B样条曲线[J]. 计算机辅助建筑, 2006,(2):15～20.

[10]左传桂, 王国昭. 多形状参数的四阶均匀B样条曲线设计[J]. 浙江大学学报(理学版), 2001,30(2):252～256.

[11]王文涛, 汪国昭. 带形状参数的均匀B样条[J]. 计算机辅助设计与图形学学报,2004,16(6):783～788.