基于混沌克隆的混杂多目标免疫优化算法
武慧虹,钱淑渠,王海英
(安顺学院 数理学院,贵州 安顺 561000)
0 引言
实际工程中,常常涉及高维的多目标优化问题(MOPs:Multiobjective Optimization Problems),高维MOPs需要同时优化多个相互冲突的目标且变量空间的维数非常高,该类问题对算法的优化能力要求极高.已有的数学优化算法极难获得理想的优化效果[1],故借鉴新的优化理论设计高级优化算法对MOPs的求解已成为当今优化领域的研究热点[4-5].
近年,大量基于群体智能的多目标优化算法(MOEA:Multiobjective Optimization Evolutionanry Algorithms)被提出:如文[6]基于生物进化理论设计遗传算法(GA:Genetic Algorithm)用于求解MOPs,仿真结果表明其具有一定的优越性,但该算法仅适应于低维的MOPs的求解[4].另一方面,研究者希望通过改进GA,提高算法求解MOPs的能力,Deb在2002年提出一种著名的MOEA (即NSGAII)[7],该算法的提出推动了进化算法在多目标优化领域中的应用,凸显智能算法求解MOPs的优越性,致使NSGAII成为很多新设计MOEA的比较对象.Hsieh等[6]基于GA设计一种分享突变算子提高MOEA对Pareto有效解的搜索能力.Guo等[7]根据个体性能排列次序及个体浓度设计MOEA的适应度,以其引导算法快速搜索Pareto有效面,并将算法用于三目标问题的求解.纵观已有MOEA知,学者们设计的重点是设计新算子提高算法的(1)群体多样性(2)开采和探索能力.
但MOEA是一种随机搜索算法,在有限的迭代数下对复杂MOPs易于出现早熟,难于获得分布均匀的Pareto有效面.而基于人工免疫系统的免疫优化算法具有高度的并行性及抗体多样性等特征,算法开采和探索能力强.2002年,Castro和Fernando基于免疫系统克隆选择原理提出一种著名的克隆选择算法(CSA:Clonal Selection Algorithm)用于MOPs,实验表明CSA用于MOPs的求解具有较大的优势[8],该研究推动了人工免疫算法在MOPs中的应用.继后,Castro和 Zuben基于免疫网络思想提出免疫网络优化算法[11],通过抑制冗余抗体增强群体多样性,实验表明算法对复杂的多模态问题表现较强的优化能力.
近来,设计免疫优化算法求解MOPs已成为人工智能领域的研究热点,特别对复杂的高维MOPs表现出较好的优化效果[12].为此,本文基于混沌规律,借鉴生物免疫系统自适应性和并行性,设计免疫算子模块,提出一种混杂多目标免疫优化算法(HMIOA:Hybrid Multiobjective Immune Optimization Algorithm).本算法(1)抗体的亲和力设计突出其被控度和抗体拥挤程度,提高算法的收敛速度及所获Pareto有效面的分布均匀性;(2)对优秀抗体采取混沌克隆的方式,提高克隆群的多样性;(3)对不同的群体采取不同的突变方式,提高算法的搜索和开采能力等.数值实验将HMIOA与NSGAII的两种提高算法(NSGAII-A、 NSGAII-B)[11]及CSA用于4类MOPs测试算法的性能,比较结果表明:HMIOA较参与比较的算法具有更强的搜索能力,克服已有算法的早熟现象,能获得分布均匀的非控Pareto有效面.
1 问题描述及相关定义
考虑如下多目标极小化问题(P)
其中,x=(x1,x2,…,xn)∈Rn为决策向量,n为向量空间维数,fi(x)为子目标函数,M为子目标数目.
定义1:对于问题P,称向量x控制向量y或y被x控制(记为:xy),如果
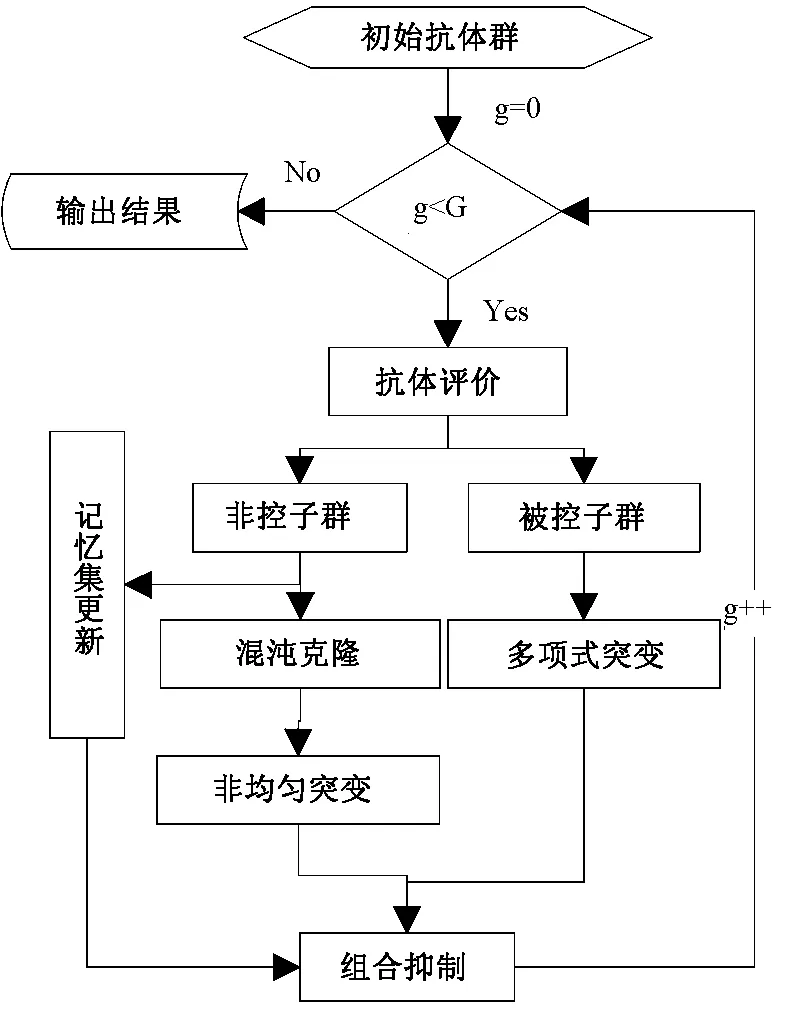
fi(x)≤fi(y)∧∃k,st.fk(x) 定义2:对有限子集X⊂Rn及向量x*∈X,若不存在任何向量y∈X,使得yx*,则称x*为Pareto有效解或非控解,所有非控解构成的集合称为Pareto有效集(记为POS),所有非控解对应的目标值构成的面称为Pareto有效面或非控面(记为POF). 基于免疫系统的特征,HMIOA算法流程如图1,图中为当前迭代数,G为最大迭代数,步骤描述为: 步骤1:初始抗体群.随机生成抗体p1,按2.2.1中式(1)生成N个抗体构成初始抗体群A,置初始代数g=0,记忆集M=φ; 步骤2:抗体评价.根据2.2.2中式(2)及(3)计算抗体群A中各抗体的被控度及亲和力; 步骤3:群体分离.按照被控度将群体A分成非控子群B和被控子群C; 步骤4:记忆集更新.记忆集M保存B中m个优秀的非控抗体,若|M|>m,则执行记忆集更新,否则转步骤5; 步骤5:混沌克隆.混沌克隆算子作用于B,获克隆群E; 步骤6:非均匀突变.克隆群E经由非均匀突变,获突变群F; 步骤7:多项式突变.多项式突变作用于被控子群C,获突变群D; 步骤8:组合抑制.组合M、F及D,获组合群 H=M⊕F⊕D. 若|H|>N,Average linkage[5]删去冗余抗体,获抗体群K; 步骤9:置n←n+1,A←K,转入Step2. 2.2.1 抗体及初始抗体群 抗体采用实数编码,假设A是N×n矩阵,则 图1 算法HMIOA流程图 A表示N个抗体组成的抗体群 其中,pi表示抗体i,pij∈R表示抗体i的第j基因位的值,n为基因长度.初始抗体群采用混沌规律生成,首先随机生成初始抗体pi,然后按式(1)生成p2,…,pN. pi+1=μpi(1-pi),(i=1,…,N-1) (1) 对应于MOPs,即:抗体pi(i=1,2,…,N)对应于MOPs的变量x,抗体群A对应于MOPs的解集,基因长度n对应于MOPs向量的维数. 2.2.2 抗体的亲和力 抗体亲和力的设计对算法的收敛速度及算法选择压具有重要的作用,在多目标优化问题中,既要求算法快速获得近似Pareto有效面,又希望所获的Pareto有效面具有均匀的分布.要使Pareto有效面分布均匀,亲和力的设计对多样性抗体的选择具有重要的引导作用,如亲和力引导算法朝Pareto面上稀疏抗体处搜索,我们可以简单引进抗体间的距离作为选择的一个标准,故本文亲和力设计如下:对于给定抗体群A={p1,p2,…,pN},根据定义1,抗体pi的被控度定义为其被控的抗体数c(pi),表达式为: c(pi)=|{y|ypi,∀y∈A} (2) 其亲和力设计为: (3) 其中,d(pi)指抗体pi的拥挤距离,具体细节如[5].从(3)式可看出,被控度越小,拥挤距离越大的抗体具有优先的选择机会. 注:根据(2)式,若c(pi)=0,抗体pi为非控抗体. 2.2.3 混杂突变 设pi为突变抗体,其突变概率设计为: (4) 其中,λ、σ为调节参数,0<λ<0.5,σ≥1,F(pi)如式(3),抗体的突变概率随算法迭代数增加而减小,并且亲和力大的抗体突变概率小,以期保证亲和力大的抗体突变程度小. 本文对不同的抗体群采取不同的突变方式,克隆群为较好的抗体群,采样微小的非均匀变异,达到精度搜索功能;对非控抗体群,采取多项式突变,抗体突变程度较大,达到大范围的搜索功能,二者通过迭代达到有机结合,提高算法的局部和全局搜索能力: (1)多项式突变 Step1 取一随机数μi∈(0,1). Step2 计算参数χi,如下 (5) (2)非均匀突变 (6) 2.2.4 混沌克隆 克隆算子主要对优秀抗体进行复制,增加优秀抗体的快速消除抗原能力,克隆体在免疫系统中经受不同的突变,存现一种混沌现象,该算子仅作用于非控抗体,克隆方式如下. ={l(p1),l(p2),…l(pη)} 2.2.5 记忆集更新 免疫系统中,记忆细胞是B细胞经抗原被激活后而留存在体内的细胞,当其再次遇到类似抗原出现时其发出快速消除抗原的能力,对应于优化问题,其是优秀的解,而在多目标优化问题中记忆细胞就是非控抗体,当算法进行下一次循环时,记忆细胞参与新抗体群的产生,以增强算法优化速度.由于记忆集中的记忆细胞随算法的迭代而剧增,为了控制细胞数目,首先删去相同的非控记忆细胞,然后根据记忆细胞的亲和力利用Average linkage[5]法消除冗余细胞,直到获规模为预定大小为m的记忆细胞集. 为了测试HMIOA的性能,本文选择如下测试问题[11]1~4测试算法的性能.其中问题1~3为二目标优化问题,问题3为三目标问题,在所有问题中向量的维数均为高维,问题难度逐渐增大,具体如下. 问题1: f(x)=(f1(x),f2(x)) 问题2: f(x)=(f1(x),f2(x)) 问题3: f(x)=(f1(x),f2(x)) 问题4: f(x)=(f1(x),f2(x),f3(x)) 其中,维数n=12,该问题为3目标问题. 在MOPs中,评价算法的优越关键是测试算法所获POF的收敛性及分布性,又由于智能算法是一种随机搜索法,具有一定的随机性,为了减少随机性对测试结果的影响,往往采取多次独立执行,从统计的角度分析算法的优越性.假设算法X与Y对MOPs分别独立执行K次所获的POS分别为Ai和Bi(i=1,2,…,K).则平均控制率(ADR(.,.))定义为 (4) 其中, 若ADR(X,Y)>ADR(Y,X),则表明算法X所获POS控制算法Y所获POS,也即算法X收敛性优越于算法Y;否则相反. 选取参与比较的算法为NSGAII-A、 NSGAII-B和CSA.其中HMIOA中参数如表1. 表1 HMIOA各算子中的参数取值 各算法的初始群规模N=100,最大迭代数G=300,各算法对每个问题分别独立执行K=30次,实验统计结果如表2~5,各算法执行一次所获Pareto有效面比较如图2~8. 表2为各算法对问题1独立执行30次所获平均控制率比较.由表知,HMIOA所获的Pareto有效面控制NSGAII-A所获的Pareto有效面的比率为13.9%,而NSGAII-A控制HMIOA的比率仅为0.5%;HMIOA控制NSGAII-B的比率为13.6%,而NSGAII-A控制HMIOA的比率仅为0.8%;HMIOA控制CSA的比率为47.8%,而CSA控制HMIOA的比率为0.0%.由上分析知HMIOA所获的Pareto有效面较大的控制其他算法所获的Pareto有效面.由图2知,虽NSGAII-A、NSGAII-B及HMIOA所获Pareto有效面整体观察均能接近理论Pareto有效面,但由图3的小区域放大知,HMIOA所获的Pareto有效面分布较均匀,非常接近理论Pareto有效面,NSGAII-A、NSGAII-B和CSA所获Pareto有效面与理论Pareto有效面的接近程度较差,且分布不均匀,CSA效果最差. 表2 各算法对问题1独立执行30次所获ADR比较 表3为各算法对问题2独立执行30次所获平均控制率比较.由表知, HMIOA控制NSGAII-A的比率为20.2%,而NSGAII-A控制HMIOA的比率仅为0.9%;HMIOA控制NSGAII-B的比率为20.7%,而NSGAII-A控制HMIOA的比率仅为0.8%;HMIOA控制CSA的比率为21.9%,而CSA控制HMIOA的比率为1.7%.由图4知,HMIOA所获Pareto有效面均能接近理论Pareto有效面,且分布均匀,而NSGAII-A、NSGAII-B及CSA所获非控面分布不均匀.由图5区域放大知,NSGAII-A在区域端点未能获Pareto有效解,其他两算法接近理论Pareto有效面较差. 表3 各算法对问题2独立执行30次所获ADR比较 表4为各算法对问题3独立执行30次所获平均控制率比较.由表知,HMIOA控制NSGAII-A的比率为5.0%,而NSGAII-A控制HMIOA的比率仅为2.4%;HMIOA控制NSGAII-B的比率为4.2%,而NSGAII-A控制HMIOA的比率仅为2.7%;HMIOA控制CSA的比率为20.3%,而CSA控制HMIOA的比率为0.0%.由图6~7知,HMIOA所获非控面均 图2 四算法对问题1所获POF比较 图3 问题1在区域(0.8,1.0)×(0,0.1)内POF比较 图4 四算法对问题2所获POF比较 表5为各算法对问题4独立执行30次所获平均控制率比较.由表知, HMIOA控制NSGAII-A的比率为8.6%,而NSGAII-A控制HMIOA的比率仅为1.8%;HMIOA控制NSGAII-B的比率为10.8%,而NSGAII-A控制HMIOA的比率仅为2.5%;HMIOA控制CSA的比率为26.2%,而CSA控制HMIOA的比率为10.5%.由图8知,HMIOA所获Pareto有效解较多,且分布均匀,而NSGAII-A、NSGAII-B及CSA所获非控点非常少,效果非常差. 能接近Pareto有效面,且分布均匀,而NSGAII-A、NSGAII-B及CSA所获非 控面的端点均未搜索到Pareto有效解. 图5 问题2在区域(0.7,1.0)×(0,0.1)内POF比较 图6 四算法对问题3所获POF比较 图7 问题3在区域(4,5)×(-1.5,-0.5)内POF比较 图8 四算法对问题4所获POF比较表4 各算法对问题3独立执行30次所获ADR比较 ADR(.,.)NSGAII-ANSGAII-BCSAHMIOANSGAII-A00.0450.2190.024NSGAII-B0.04800.2160.027CSA0.0020.00300HMIOA0.0500.0420.2030 表5 各算法对问题4独立执行30次所获ADR比较 本文基于生物免疫系统的主要机理及特征,提出一种混杂多目标免疫优化算法.利用不同类型的高维多目标问题测试算法的性能,选取著名的多目标进化算法NSGAII-A及NSGAII-B和一种克隆选择算法CSA参与比较,结果表明本文算法所获非控面较大的控制其他算法所获的非控面,Pareto有效面分布非常均匀,搜索范围较广,较接近理论Pareto有效面,而其他三算法所获得Pareto有效面效果较差.接下来我们即将作更深入理论研究,探讨其收敛性及算法复杂性. [1]徐志丹,莫宏伟.生物地理信息优化算法中迁移算子的改进[J].模式识别与人工智能,2012,25(3):544-549. [2]武慧虹,钱淑渠,李 俊.动态环境优化问题及算法综述[J].吉林师范大学学报(自然科学版),2013,34(2):121~124. [3]刘春英.粒子群融合蚁群算法多配送中心车辆路径研究[J].吉林师范大学学报(自然科学版),2013,34(3):88~91. [4]Pilát M,Neruda R.An evolutionary strategy for surrogate-based multiobjective optimization[C]// IEEE Congress on Evolutionary Computation (CEC),2012:1-7. [5]Kim J H,Han J H,Kim Y H,et al.Preference-Based Solution Selection Algorithm for Evolutionary Multiobjective Optimization[J].IEEE Transactions on Evolutionary Computation,2012,16(1):20-34. [6]孔德剑.基于改进的遗传算法的多目标优化问题研究[J].计算机仿真,2012,29(2):213-215. [7]Deb K,Agrawal S,Pratap A,et al.A Fast elitist nondominated sorting genetic algorithm for multiobjective optimization:NSGA-II.IEEE Transactions on Evolutionary Computation,2002,6(2):182-197. [8]Hsieh S T,Chiu S Y,Yen S J.An Improved Multi-Objective Genetic Algorithm for Solving Multi-objective Problems[J].Appl.Math,2013,7(5):1933-1941. [9]Guo X,Wang Y.A Hybrid Simplex Multi-Objective Evolutionary Algorithm Based on A New Fitness Assignment Strategy[J].Journal of Computers,2013,8(2):284-289. [10]de Castro L,Fernando J.Learning and optimizationusing the clonal selection principle[J].IEEE Transactions on Evolutionary Computation,2002,6(3):239~251. [11]Freschi F,Coello C A C,Repetto M.Multiobjective optimization and artificial immune systems:a review[J].Handbook of Research on Artificial Immune Systems and Natural Computing:Applying Complex Adaptive Technologies,2009,4:1-21. [12]Farina M,Deb K,Amato P.Dynamic Multiobjective Optimization Problems:Test Cases,Approximations,and Applications[J].IEEE Transactions on evolutionary computation,2004,8(5):425-442.2 算法描述及算子设计
2.1 算法描述
2.2 算子设计
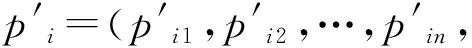
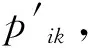
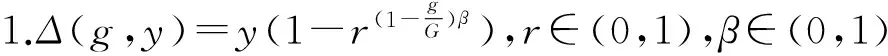
3 测试问题及评价准则
3.1 测试问题
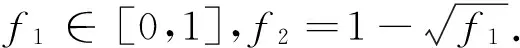
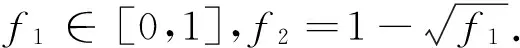
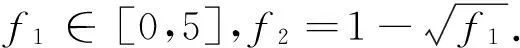
3.2 评价准则[10]
4 数值实验
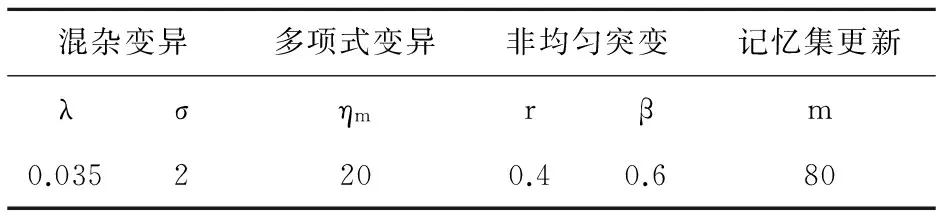
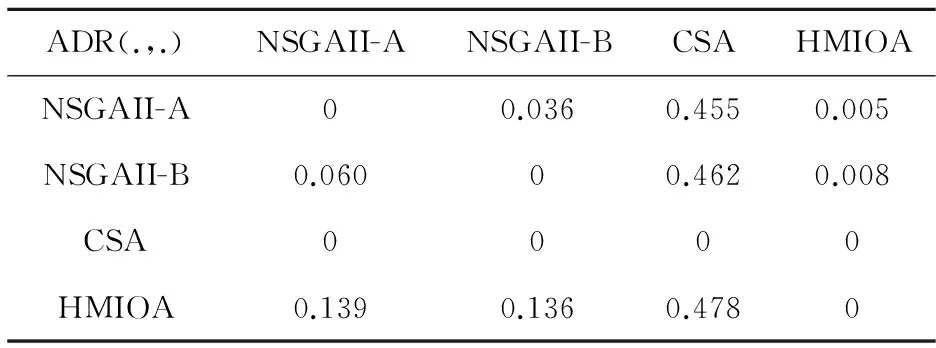
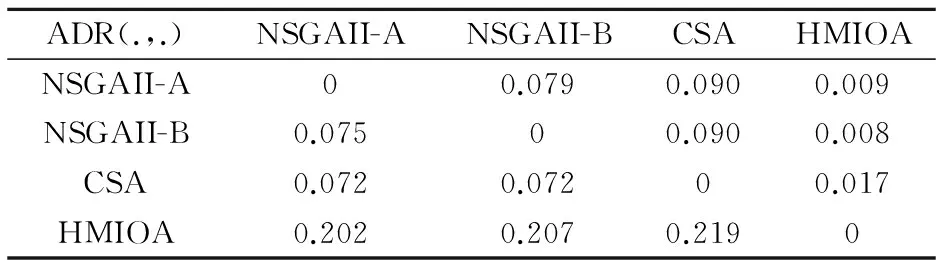
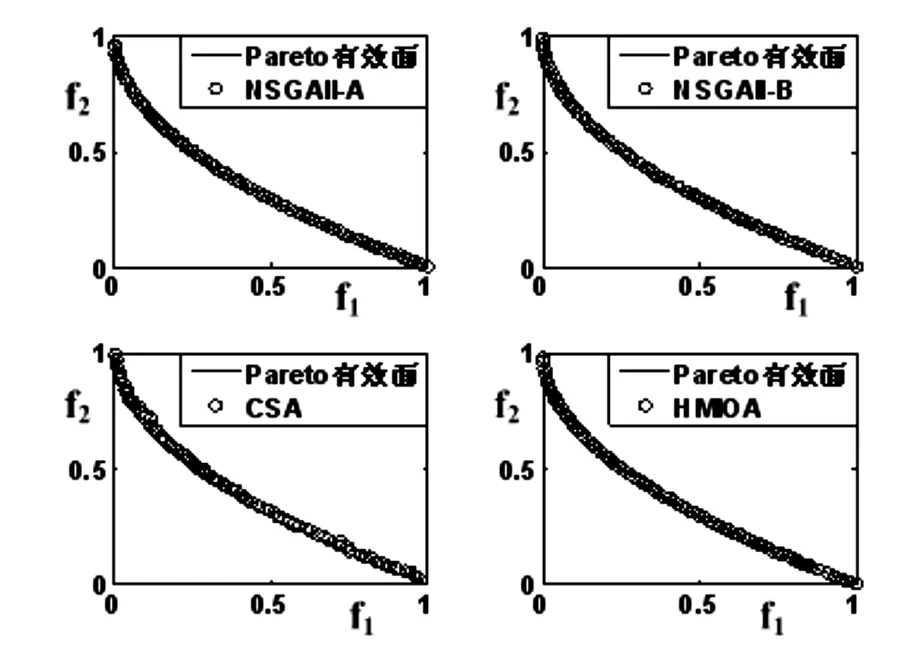
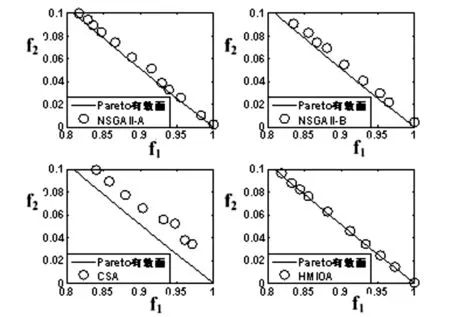
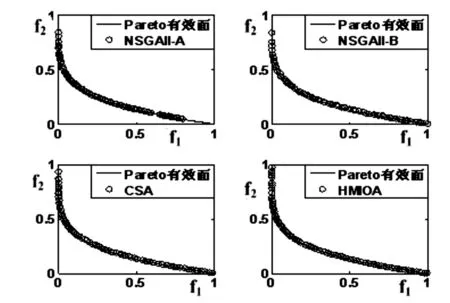

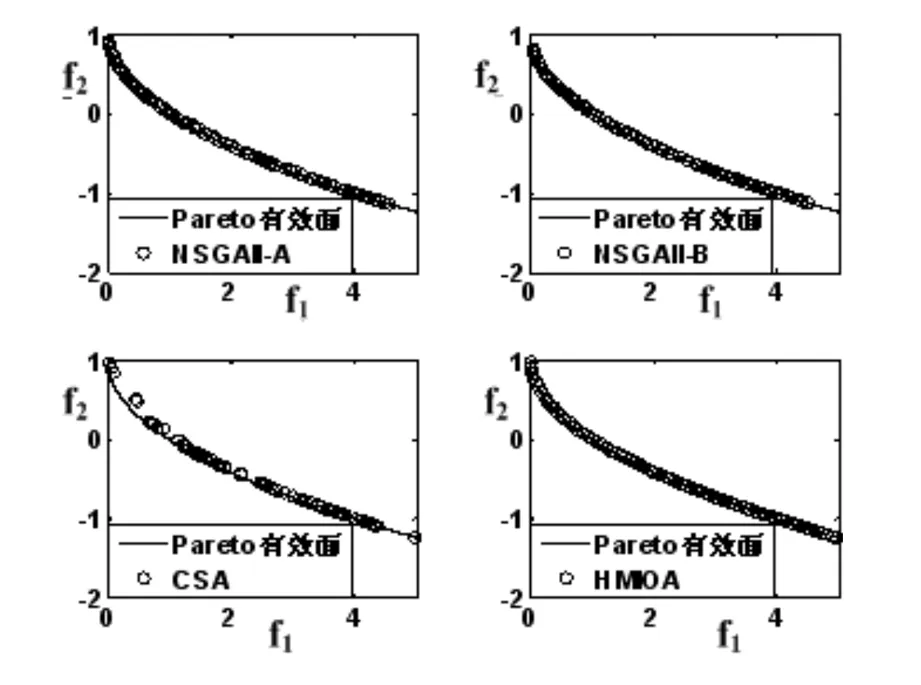
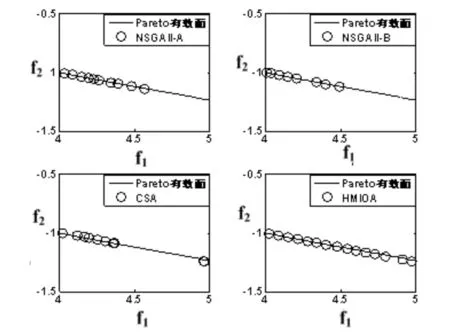
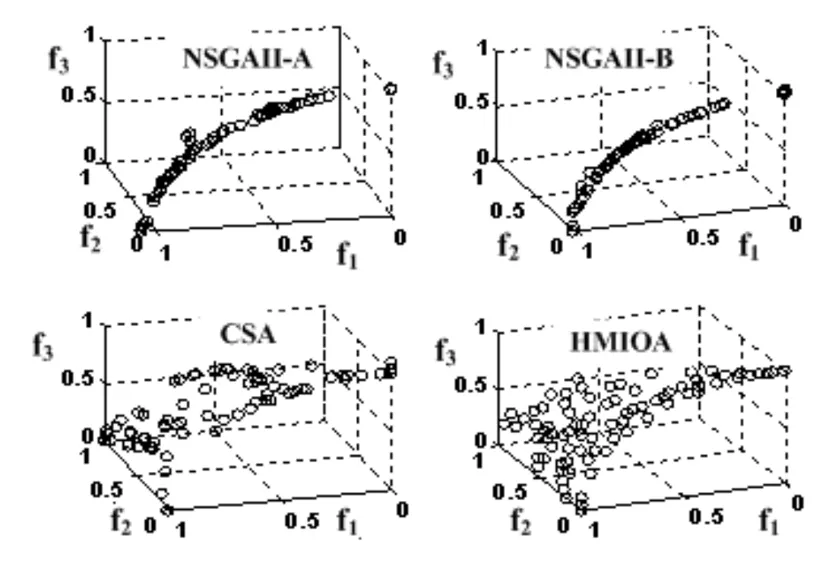
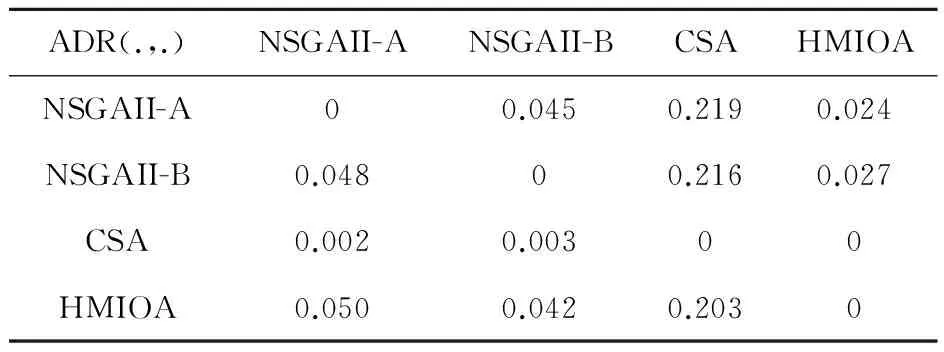
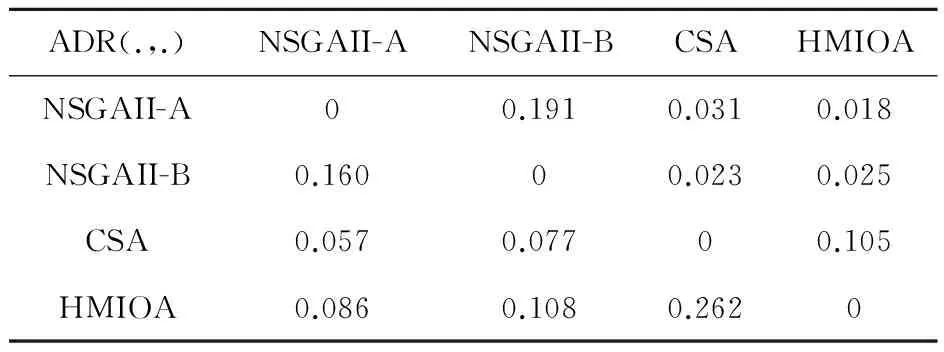
5 结论及进一步工作

