局部放电高性能电流传感器的设计

戴旭益，杨 珀，沈剑荣，陈 炯

(1.上海电力学院，上海 200090;2.国网安徽省电力公司，安徽合肥 230061;3.国电浙江北仑第一发电有限公司，浙江宁波 315800)

局部放电检测是检验设备绝缘状态的重要试验，局部放电在线监测是近年来非常热门的一个研究课题.［1］基于罗氏线圈结构的电流传感器不仅可以实现对一些微小的绝缘缺陷引起的电缆局部放电微信号的检测，而且可以在线监测电缆和发电机组绝缘介质等设备的绝缘状态，［2-3］在电缆或发电机组不停运的情况下，获取内部绝缘老化状况，并根据绝缘状态信息制定维修策略，以保证电缆的安全运行.

罗氏线圈由于传递线性度好、测量频率宽、工作速度快，以及无磁饱和的问题而广泛应用于电力系统高压侧电流的检测、保护和控制.［4］本文分析了罗氏线圈的原理，建立了相应的高频模型和等效电路，结合软件仿真设计出合适的传感器参数，然后通过边界性能良好滤波器进行信号处理，以提高传感器的幅频特性.最后从其灵敏度、工作频带及通带到阻带的滚降速度等方面检验了传感器的性能.

1 电流传感器原理与高频模型分析

电流传感器是一种基于电磁感应信号耦合的线圈，如图1所示.其基本原理是:一次侧初始信号电流流过电流传感器几何中心，在初级线圈交流电流的作用下，磁芯中产生交流磁通，使二次侧线圈感应出电流，通过串接的负载阻抗得到高频电流分量.［5-6］

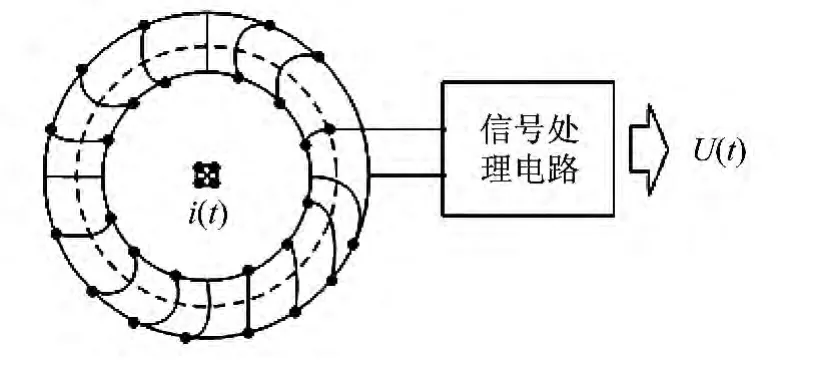
图1 罗氏线圈结构电流传感器示意

采用罗氏线圈进行测量时，载流导线从罗氏线圈的几何中心穿过，如果线圈的平均半径为r，线圈截面上各处磁通量可视为相等，则可以得到:

同时通过电磁场理论可知，线圈交链的磁链而产生的e与初级电流i的变化率di/dt成比例，因此当测量线圈在绕线均匀情况下得到的单位长度线圈交链的磁链为:

式中:B=μH.

对式(2)进行处理可以得到整个线圈交链的磁链，然后对其进行微分处理，得到感应电动势为:

图2为罗氏线圈等效电路模型.［6］

由图2可知:

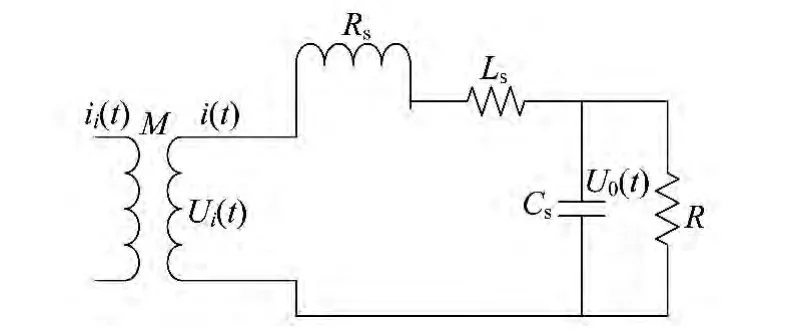
图2 罗氏线圈等效电路

将式(4)、式(5)、式(6)联立进行处理，经过拉普拉斯变换后计算得到该高频线圈S域的传递函数为:

在fH远大于fL且电阻线圈内阻和采样电阻较小的情况下有:

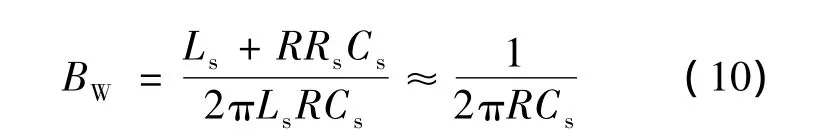
在高频信号作用下，杂散电容的作用不能忽视.分析线圈在谐振角频率ω0时的灵敏度:

可知，耦合高频信号时，线圈的灵敏度是由其自身电感Ls，电阻Rs，杂散电容Cs，外接电阻R共同决定的.虽然在高频信号作用时，决定线圈灵敏度的因素比较复杂，但可以容易得到输出电压幅值跟外接积分电阻成正比、与传感器副边线圈匝数成反比的变化关系.在确定传感器磁芯材料、结构形状，以及内径、外径和高度后，改变线圈匝数和外接积分电阻的大小，就可以调节电流传感器的工作频带和灵敏度.

综合工作频带和灵敏度可以看出，增加积分电阻可以提高灵敏度的同时会影响线圈的工作频带;增加副边线圈匝数可以增加响应带宽的同时会影响线圈的灵敏度.因此，在磁芯外部特性确定后，线圈内部特性参数(如匝数和积分电阻的大小)存在一个最佳的匹配问题，决定着传感器的工作性能.

2 参数设定与仿真分析

设置传感器初始参数，并在Matlab软件中进行仿真，寻找因参数变化引起传感器特性变化的规律.经过多次参数仿真对比，本文设定的标准传感器参数如下:线圈外径为17mm;线圈内径为11.5mm;骨架高度为12.5mm;线圈匝数为30;铜线直径为0.4mm.选取磁导率为200的镍锌铁氧体作为传感器磁芯.

计算的结构参数设置为:M=5.9 μH，Ls=177 μH，Cs=270.9 pF，Rs≈ 1.129 Ω，ρ=0.017 78 Ω·mm2/m.然后对传感器进行仿真.仿真结果如图3所示.

图3 传感器仿真结果

由图3可知，传感器在-3 dB时达到设计的最大灵敏度11 dB，在0.1～0.8 MHz的工作频段内保持稳定的灵敏度.

由传感器模型分析可知，线圈的工作频带和灵敏度与所绕制的匝数和选用的自积分电阻的大小有关.对于这两种不同的参数，在仿真软件中通过逐次改变其中一个参数来观察对线圈幅频特性的影响，然后得出两个参数的最佳匹配值.［7］

改变自积分电阻的大小可以改变线圈的幅频特性，如图4所示.当选用1 000 Ω的自积分电阻时，设计的最大灵敏度约为30 dB.线圈工作频带的下限在1 MHz左右才达到设计的最大灵敏度.这样虽然能够避开改频段内的噪声干扰，但是在捕捉频率相对较低段局部放电信号的能力方面有所下降，并且最大灵敏度处的工作频带远小于局部放电信号的带宽.如果持续增加自积分值，则原始信号的耦合能力更为减弱.当选用10 Ω的的自积分电阻时，设计的最大灵敏度为-10 dB，下限频率将减少到10 kHz，大大增加了工作频带内耦合干扰信号的可能.为使灵敏度和带宽同时满足要求，将R取为100 Ω.由仿真结果可知，积分电阻在100 Ω时，传感器的灵敏度和工作频带都能很好地满足局部放电信号的测量要求.

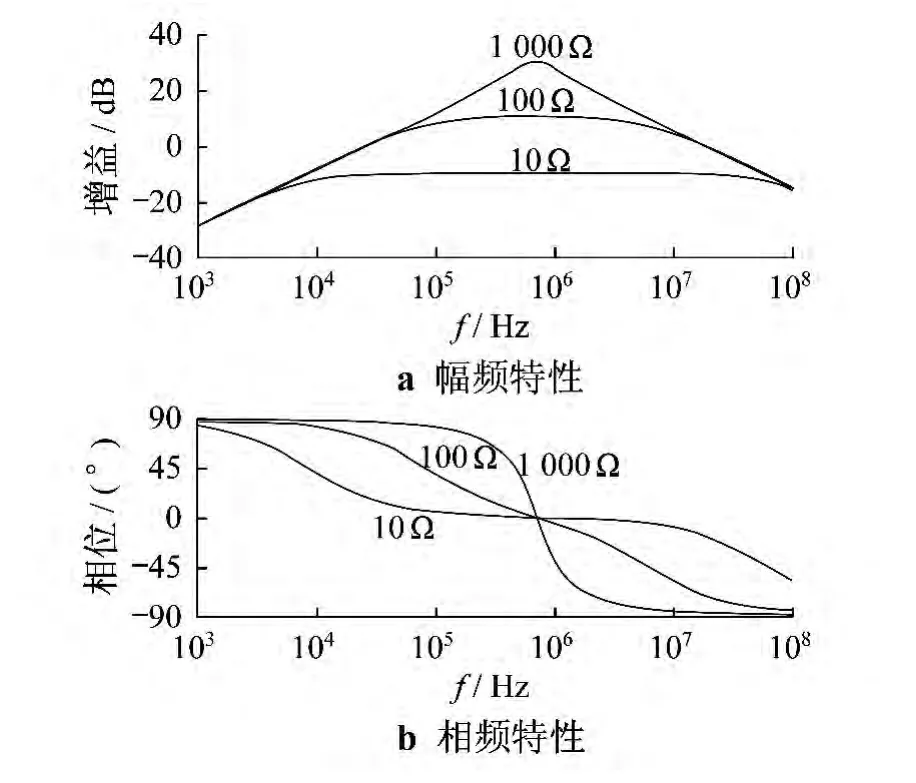
图4 积分电阻影响下的变化规律

改变绕制匝数可以改变线圈的幅频特性，如图5所示.当增加线圈匝数为90匝时，设计的最大灵敏度约为1 dB，线圈在10 kHz时已达到设计的最大灵敏度，工作频带为0.01 ～1.0 MHz.由于干扰信号一般在1 MHz以下，该工作频带导致线圈抗干扰信号的能力有所下降.当减少线圈匝数为10匝时，最大灵敏度为20 dB，工作频带为1～10 MHz.该工作频带对于低频段局部放电信号的捕捉能力较弱，在0.1～1.0 MHz内的信号不能被耦合过来.当匝数为30匝时，传感器灵敏度和工作频带都能很好地满足局部放电信号的测量要求.

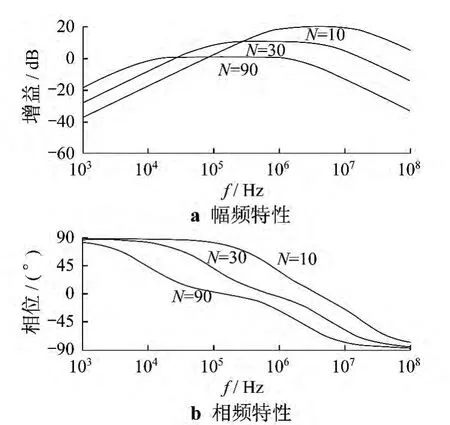
图5 绕线匝数影响下的变化规律

根据仿真结果进行参数调整，最终确定匝数为30匝，积分电阻为100 Ω，工作频带为0．1～8．0 MHz，传感器的工作频带平坦且有12 dB的最大灵敏度．

3 信号处理电路设计

对传感器耦合到的信号，一方面要进行滤波处理，另一方面由于传感器幅频响应曲线在通带和阻带临界处的降落速度不够理想，为提高临界处的信噪比，综合考虑下设计了如图6所示的6阶带通滤波单元．

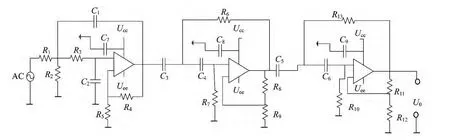
图6 信号处理电路

信号处理部分的频带为0．1～10 MHz．前级采用2阶高通滤波器，通带到阻带临界部分的滚降速度为40 dB/10倍频程，后级采用4阶低通滤波器，临界部分的滚降速度为80 dB/10倍频程，边界滚降性能良好．整个滤波电路的通带增益是电压分压器比值与滤波器部分增益的乘积，取值为1，故有:

式中:AVF1——巴特沃斯滤波器特定阶数设定下的增益．

4 测试结果

搭建波形发生器产生各种频率的正弦波，用高频电容进行分压，再用一个相同的高频电容获得所需的电流信号．将电流信号线尽可能垂直于传感器几何中心穿过，用示波器测取经信号处理电路的电压信号．为了增大线圈的互感，提高线圈的抗干扰能力，采用回绕线方式．测试结果如图7所示．

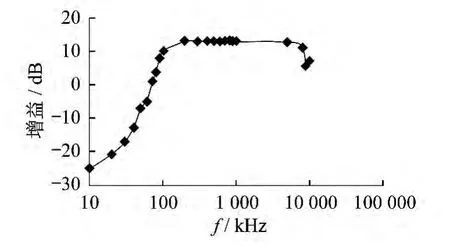
图7 加装处理电路的电流传感器幅频特性

带信号处理电路的电流传感器通带平坦，频率低于下限频率处的曲线以40 dB/10倍频程降落，频率高于上限频率处的曲线以80 dB/10倍频程迅速衰减，处理电路在滤波的同时提高了通带和阻带临界处的信噪比，增加了传感器的耦合能力．

尽管实测传感器和仿真幅频曲线存在一定的灵敏度偏差，但已达到预期幅频要求．偏差原因可能是外界磁场对罗氏线圈造成的影响、母线偏心放置时引起的误差，以及绕线重叠造成的误差等.通过改进绕组的缠绕技术和屏蔽措施(屏蔽壳套)，可以在一定程度上减少传感器的误差.［8］

5 结论

(1)分析了高频电流传感器模型，设置了基本参数对其进行仿真，通过变化规律，确定积分电阻和传感器匝数合适的匹配值，设计制作了性能良好的电流传感器，适合测量0.1～8.0 MHz频段内的局部放电信号.

(2)加装信号滤波处理电路，提高了传感器幅频特性通带到阻带的边界性能，低通部分通带到阻带以80 dB/10倍频程快速降落，能耦合到信噪比高的信号.

(3)加装信号处理电路的电流传感器幅频特性的测试表明，电流传感器在0.1～8.0 MHz的工作频段内具有灵敏度高、工作频带宽、通带曲线波动率小的特点，总体工作性能良好.

［1］ 罗俊华，马翠娇，邱毓昌，等.35kV及以下XLPE电力电缆试验方法的研究［J］.电网技术，2000，24(12):58-61.

［2］ 刑德强.XLPE电力电缆检测技术［J］.电工技术学报，2006，21(11):7-8.

［3］ 陶诗洋.基于振荡波测试系统的XLPE电缆局部放电检测技术［J］.中国电力，2009，42(1):98-101.

［4］ 彭丽.10kV/35kV电子式电压/电流互感器研究［D］.武汉:华中科技大学，2004.

［5］ 张岗.光电混合式电流互感器的设计理论及其在电力系统巾的应用［D］.武汉:华中理工大学，2000.

［6］ 葛景滂，邱昌容.局部放电测量［M］.北京:机械工业出版社，1984:262-268.

［7］ 邹积岩.罗哥夫斯基线圈测量电流的仿真计算及实验研究［J］.电工技术学报，2001，16(1):81-84.

［8］ 申烛，钱政，罗承林.Rogowski线圈测量误差分析和估计［J］.高电压技术，2003，29(1):6-8.