“相遇”类问题s-t图像的表征及意义分析*

张建奋

(广州市白云区教育发展中心，广东广州 510440)

图像表征是指用连续性图像，离散性图像或图表等来描述物理过程、情景或推理过程.有研究指出，不同形式的曲线对不同的认知任务具有不同的表征绩效并引起不同的认知行为，可以根本地改变决策行为.“相遇”是运动学中重要的问题类别.在问题解决中，面临关键特征即临界条件的确定，而临界条件往往是隐含的问题条件，只有通过不同的表征才能发现.用s-t图像表征分析临界条件，有直观和易分析的特点，对解题策略的确定有独特效果.现以2个质点相遇为例，对图像表征及意义进行分析.

1 质点的“相遇”，直观体现在图像的“交点”的存在

例1.一小球以20 m/s的速度竖直上抛出去，与此同时，在距小球4 m正上方有一气球以一定的速度向上匀速运动，求小球可能击中气球的最长时间和最短时间.

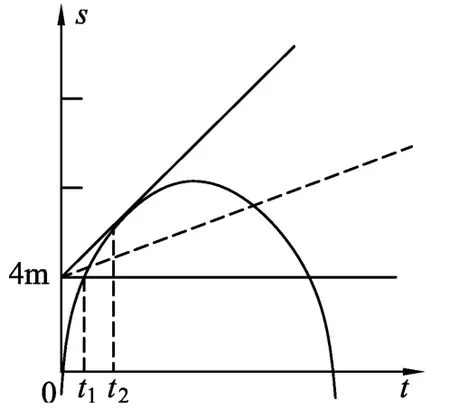
图1

分析:本题要确定质点的“相遇”的临界条件.题目中气球的速度未定，如何确定小球击中气球的最长时间和最短时间对应的临界速度是本题的关键所在.如图1所示，s-t图像表示小球与气球的运动过程，小球击中气球的时刻即直线与抛物线的第1个交点对应的时刻.依题意，气球的速度未定即直线方程斜率未定(但v＞0，即气球以一定的速度向上匀速运动).由图中可看出v→0时即直线与抛物线的第1个交点对应的时间t1为最短时间，直线与横坐标轴相切时，与抛物线的切点对应的时间t2为最长时间.

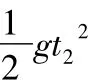
用s-t图像表征质点的“相遇”，可直观体现在图像的“交点”的存在.有简捷和直观的特点，便于对“相遇”的分析，常作为解题前的定性分析，或是解题后对解题结果的定性判断.

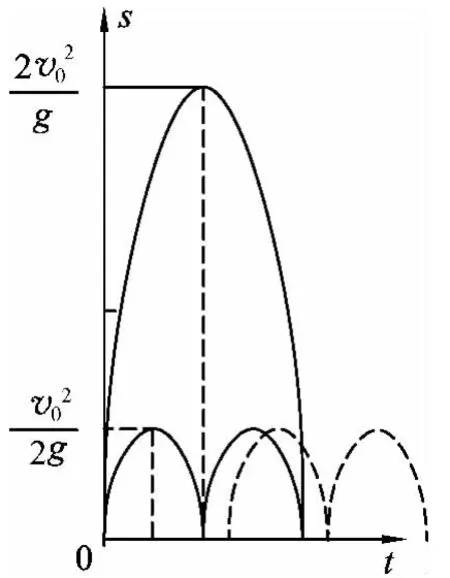
图2

2 相遇“时间间隔”，通过图线平移出现“交点”的发现间隔时间

例2.以初速度为2v0由地面竖直上抛一物体A，然后又以初速度v0由地面竖直上抛另一物体B，若要两物体在空中相遇，试求:抛出两物体的时间间隔.

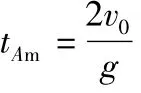
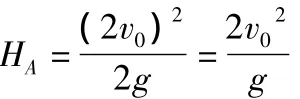
“时间间隔”意义是一种抽象不易用语言描述的.但用运动图像表征的好处是可以直观地表达出来.

3 用s-t图像呈现的关系，抓住“变式”特征，动态分析物理量变化的关系，寻求隐含的临界条件

从例1的变式为例进行分析.原题以气球匀速运动未定的情况下来分析，同样，在其他情况下还有不同的“变式”特征.

变式1:如图3给定气球匀速运动的速度，而小球竖直上抛的初速度可动态变化，画出图线可分析小球竖直上抛初速度变化后，图线的交点(相遇点)位置和时间的变化，还可分析出刚好相遇的条件(即相切或只有1个交点的对应的情况).

变式2:给定了气球匀速运动的速度和小球竖直上抛的初速度，而抛出点相距的可动态变化，(如图4)，可定性看出相遇点(第1个交点)随距离的变化关系，也可分析出刚好相遇的条件(即只有1个交点或刚好相切的情况).

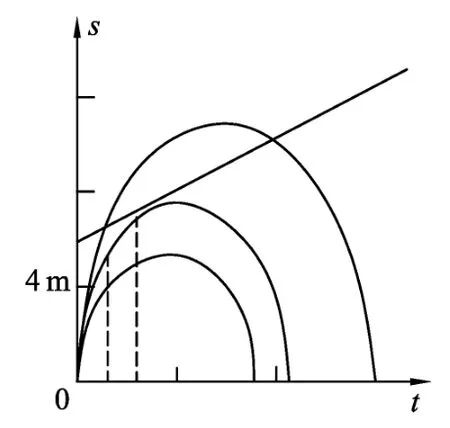
图3

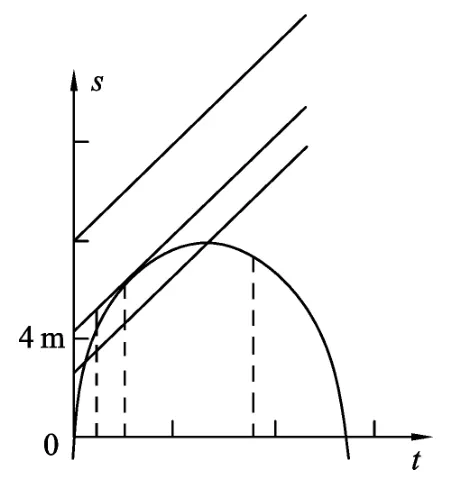
图4

显然，通过“变式”进行拓展，可以通过图线表征直观去理解物理过程的意义.变式1是通过直线与“曲线族”的相切与相关关系(如图3)，变式2是曲线和“直线族”的相切与相关关系(如图4)，通过定性动态分析，可较易找到相遇点的变化和判断发生相遇的条件.

4 探究s-t图像分析“相遇问题”隐含临界条件的基本思路

相遇问题在分析隐含的临界条件时，用s-t图像会比vt图像具有直观和便于定性分析的特点.但教学上要把握好几个最基本的思路:(1)s-t图像分析两质点“相遇”问题，一定要在同一坐标系中画出运动质点的运动图像进行分析.(2)两质点“相遇”隐含着s-t图像中，两运动图线有“相交”的点，还要具体分析相交点的实际物理意义.(3)对“隐含”条件的分析，要从问题情景或条件所隐含的物理意义去讨论(如斜率、相交、相切等)，通过图线的动态分析，去寻求隐含的临界条件.

以上仅以s-t图像为例，探讨“相遇”类问题的表征及意义.用不同分析视角，对学习者来说会有不同的表征，就会呈现不同的意义.图表表征能够支持操作者直接识别问题特征和进行推断，使问题信息更具体和更具有可解释性、可加工性.这方面确实还有不少可研究的空间.

1 Stenning K，Oberlande J.A cognitive theory of graphical and 1inguistic reasoning::Logic and implementation.Cognitive Science，1994，19:97-140.

2 张建奋.适应性与适切性:理教学行动的结构分析［M］.广州:暨南大学出版社，2012:30-58.