基于AdaBoost的链路预测优化算法

吴祖峰，梁棋，刘峤，秦志光

（电子科技大学 计算机科学与工程学院，四川 成都 610054）

1 引言

链路预测(link prediction)问题源于复杂网络研究领域，目的是根据目标网络的观测数据（节点和关系）预测该网络中节点间可能存在的关系和将会产生的关系[1]。典型的链路预测问题解决方案包括优先链接原则和森林火灾模型[2]。

链路预测采用的主要研究方法是依据当前网络的拓扑结构来评估节点间关系的重要性，据此推断节点间存在关系的可能性。链路预测方法可用于恢复目标网络观测数据中的缺失信息[3]，也可以用于研究网络的衍变[1]。此外，由于仅依赖于网络拓扑结构进行推断，所以可以将其推广到多种类型的网络中，如社交网络、生物领域、合作网络等。随着一些链路预测算法开始在商业领域得到应用，与之相关的研究已经成为一个热门领域，其中，基于图的链路预测算法的研究在近年来受到了广泛重视[4]。例如，Facebook采用基于有重启的随机游走（RWR, random walk with restart）算法预测用户的朋友关系，据此提高好友推荐的成功率[5]。

基于网络拓扑图的链路预测算法主要包括基于节点邻居的相似性、基于最大似然估计[6]以及基于概率模型3种类型。代表性算法包括基于局部信息相似性的共同邻居(common neighbor）算法、基于路径相似性的 Katz算法和基于随机游走相似性的RWR算法。其中，基于节点邻居相似性的链路预测算法研究较早，因其性能表现相对良好，多数算法研究工作均将其作为基准参考算法[5]。另一类取得实际推广应用的方法是基于随机游走的链路预测算法。这些算法的基本思想都是对图中节点所有可能的组合进行排序，选择出其中最可能出现在新图中的节点对（即图中的边）。

2007年，Liben-Nowell D等人在链路预测方面所做的开创性工作引起了学术界对于该问题的重视[1]。其提出的一些基本方法也成为链路预测研究中进行算法性能比较的Benchmark算法。其中，被广泛引用的算法包括：共同邻居（CN, common neighbor）法、杰卡德系数（JC, Jaccard's coefficient）法和Adamic/Adar（AA）法。所谓共同邻居法，是指2个节点的共同邻居节点的数目，Kossinets和Watts使用该方法分析了一个大规模的社会网络，发现共同朋友越多的2个人越有可能在未来成为朋友[7,8]。杰卡德算法是共同邻居法的标准化方法，表示2个节点是否含有一个共同特征[9]。Adamic/Adar法是由Adamic和Adar提出的一种方法[10]。在合作网络中，作者w与作者u、v均有合作，如果w和u、v以外的作者没有合作关系，那么u、v之间更有可能合作。

除上述3种Benchmark算法之外，本文还引入了近年来受到广泛关注的基于随机游走相似性指标的重启的随机游走（RWR）算法作为参照[11]。该方法可以视为 PageRank算法的扩展，二者的区别在于RWR算法假设随机漫步者每走一步都以一定概率返回初始位置。该算法已经被应用于推荐系统的算法研究之中[12]。

表1给出了上述算法的名称以及计算公式。其中，符号Γ(u)表示节点u的邻居节点集合。

表1 预测算法名称及公式

Polikar R 等人关于集成学习（ensemble learning）的研究表明，在对各种问题进行决策时，人们通常会在决策前寻求多种可能的选择，通过对这些选择进行权衡通常能够做出最明智的决定，因此相对于单一的专家系统而言，多个不同性质专家系统的集成会产生更为有利的结果。同样的原则适用于统计机器学习领域，即单一的分类器在不同问题上的泛化表现可能不同，而按照一定的原则对多种分类器进行集成则有可能实现算法性能的均衡和提升，减少因分类器选择不当而导致的泛化性能表现过差的风险[13]。例如，由多个医生对病人会诊，不仅有助于降低误诊的风险，而且有助于得出最优的诊断结果。Boosting方法是一类有效的集成学习方法，研究表明它能够提高任意给定学习算法的准确度[14]。本文采用经典的 Adaboost (adaptive boosting)算法作为链路预测算法的集成学习器[13]。

AdaBoost是最具代表性的 Boosting算法，由Freund 和 Schapire 于 1995年提出，现有的各种Boosting算法都是在 AdaBoost算法的基础之上发展而来的。其突出优点是不需要任何关于弱学习器的先验知识，样本分布的改变取决于样本是否被正确分类。算法的基本思路是赋予分类正确的样本以较低的权值，同时调高分类错误样本的权值，作为后续学习器的输入，最终得到的结果是弱分类器的加权组合。AdaBoost是一种有很高精度的分类器，能够有效避免过拟合。

近一两年来，在基于拓扑的链路预测算法的研究中，在对已有算法的改进以及新算法的提出方面，仍然还没有出现有突破性的成果，基于拓扑的链路预测算法的召回率依然较低。

通过本文的研究发现，现有的主流链路预测方法的预测结果并不完全相交，直觉上认为有可能利用算法结果的叠加提高召回率。但是，直接累加求和并不可行，因为会降低总的算法精度（如图1所示）。据此考虑采用基于Boosting的集成学习方法对其进行改进[13]。首先将链路预测问题看作二分类问题，对下一时刻网络中每一条可能存在的边（节点对），其分类结果为2类：存在或不存在。接下来借用Boosting方法通过错误反馈提升弱学习算法得到强学习算法的思想，根据一定的原则选取若干链路预测算法作为弱分类器，基于 AdaBoost算法提出并实现了一个新的算法。在本文所使用的论文合作网络数据集以及邮件通信数据集上的实验结果表明，本文提出的算法对预测算法的准确度和召回率都有一定的提高。

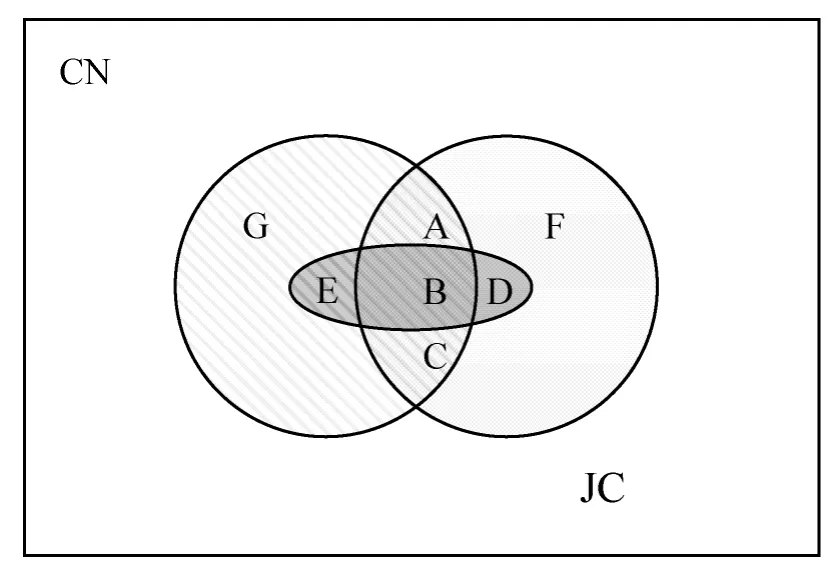
图1 CN和JC的预测范围交集以及正确结果交集

2 算法设计

2.1 算法改进的依据

为了与现有工作做比较，本文选取arXiv论文合作网络数据作为数据集，数据的选择是参照Liben-Nowell D和Leskovec J的工作[5]选取，以便对实验结果进行比较。数据的获取是使用爬虫从www.arxiv.org网站分别爬取4个领域的文章作者列表。爬取策略参见3.1节。以Hep-ph领域数据为例，如果2个作者出现在同一篇文章的作者列表中，则为这2个节点生成一条边，代表他们有进行过合作。笔者以 1994～1996年作为预测的训练集合，1997～1999年作为预测的测试集合。为所有度为3以上的活跃作者做预测。表2可以看到几种常用的链路预测算法在数据集Hep-ph上预测新生成边的正确结果的交集。每 2种算法之间都有交集，但并不完全重合。直觉上可以合并正确结果以扩大正确预测范围。

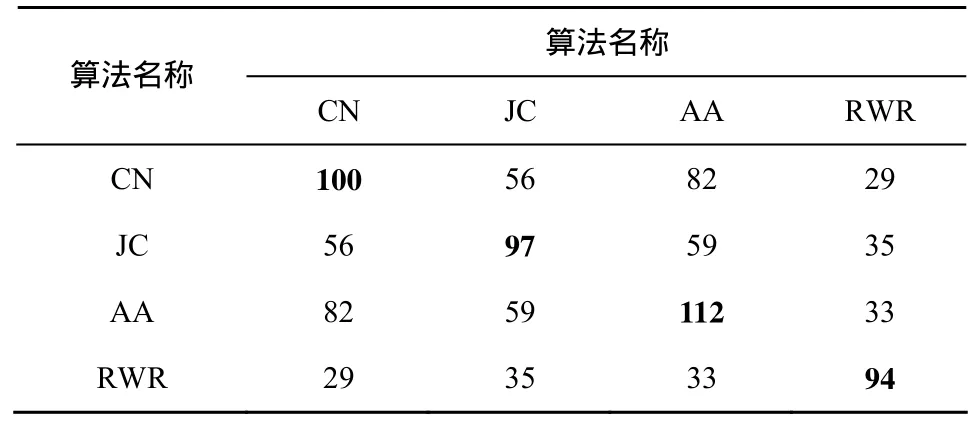
表2 每2个算法预测的正确结果的交集

但是直接合并预测结果会使得预测范围过分扩大，减少预测精度。以算法CN和JC为例。如图1所示。左右两侧的圆形区域分别代表算法CN和算法 JC的预测结果，每个圆形区域表示的节点对的数目为1 500。区域A∪B∪C表示二者预测结果中相同的节点对，数值为692。区域A∪B∪C∪D∪E∪F∪G表示二者预测结果的并集，节点对数目为2 308。区域B∪E以及区域B∪D分别表示算法CN以及算法JC预测结果中正确的部分，节点对的数目分别为100和97。相应的区域B为二者正确预测结果的交集，节点对数目为56。

算法 CN、JC预测的准确率分别为 9.52%和9.23%。如果对 2个算法的预测结果只是做简单的合并，即预测结果是区域A∪B∪C∪D∪E∪F∪G。正确预测值是区域E∪B∪D，节点对数目为141。准确率变为6.10%。由此可以看出，简单的合并会使得准确率下降。

由此考虑采用Boosting的思想。采用每种算法的预测结果，根据错误反馈，将弱学习算法提升为强学习算法能够有效缩小预测范围，即缩小图中 2个圆形区域的并集。扩大正确预测结果的并集，即图中的黑色部分。有效地提升预测精度。

2.2 弱分类器的选择

基于局部信息相似性的链路预测算法是经典算法，因其性能表现相对较好，多数算法研究工作均将其作为基准参考算法。在链路预测中，发现距离为2的2个节点链接的概率大于距离值为其他的节点对[5]，局部信息相似性的算法在链路预测中仍占重要地位，本文选取其中表现相对良好的CN、JC、AA作为弱分类器。而RWR作为基于随机游走的预测算法，因其良好表现，也将之选取作为弱分类器。

Wuv表示节点间已经链接的边的数目。在合作网络中，即二者已合作文章数，图2表示在Hep-th数据集上，作者在1994～1996三年间已合作文章数目与他们在1997～1999三年间再次合作概率的关系图。随着已合作文章数目的增长，两人间再次合作的概率也越来越大。当已合作文章数大于10篇时，两人再次合作的概率可以达到90.32%。可以猜想他们已经形成一种长期合作的关系。已合作文章数目大于2的作者再次合作的概率均超过了50%。根据以上描述，对于已经合作过的人来说，如果他们已有合作，那么有1/2的可能他们会继续合作下去。所以在对节点间当前已有边的情况进行预测时，考虑将Wuv选为弱分类器。

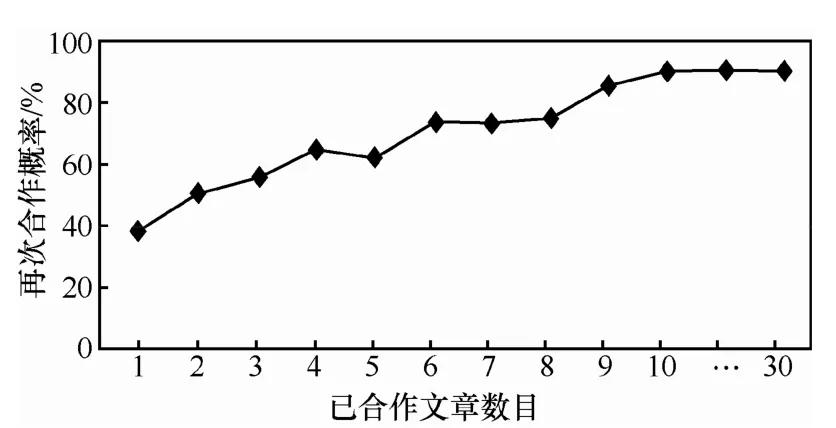
图2 已合作文章数目与再次合作概率关系

2.3 算法概述

算法1给出了算法的基本流程。对于一组长度为m的预测训练集合C。Ω表示xi被分类的类型值的集合。对于xi，如果它确实出现在下一时间段的图中，则yi=1，反之，yi=-1。接着按照式(1)为每个样本的权重赋初始值。

算法1 ALP算法伪代码

给定：长度为m的有着样本标签yi∈Ω,Ω={-1,+1}的预测训练集合

Initialise Weights：

每个样本最终预测结果为

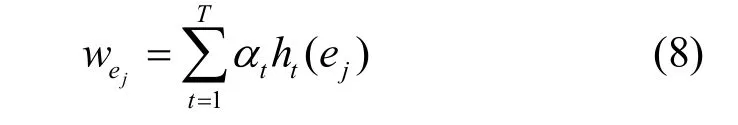
对于每一种预测算法t，计算出C中每一对节点u、v的Suv，然后进行降序排列，选取前m个节点对，形成集合P，表示算法t判定这些节点对会在下一时刻的图中存在，剩下的形成集合Q，表示算法t判定这些节点对不会在下一时刻的图中存在。m是集合C中实际存在于下一时间段的图中的节点对数目。将预测算法t看作一个弱分类器t，t做出的假设为ht。根据式(2)，如果xi∈P，则ht(xi)=1，反之，若xi∈Q，ht(xi)=-1。

进行T次循环，t=1,…,T：每一次循环时，首先为每个分类器计算当前的错误率。对于每一个样本xi，将分类器t对其的分类与其本身所属类型相比，如果不一致，则在此分类器的错误率上加上该样本xi的权重Dt(i)。按照式(3)计算并找出错误率最小的分类器作为当前的分类器。但是如果εt大于1/2。就停止算法。以式(4)对εt进行归一化处理，0＜αt＜1，αt作为当前分类器t的投票权重。更新每个样本xi的权重，如果xi被当前分类器错误分类，则它的权重上升。相对来说xi如果被正确分类，那么它的权重就降低了，具体按照式(5)、式(6)升级每个样本xi的权重。T次循环后，得到每个分类器的投票权重αt。

预测测试集合D中，使用ej表示D中的每个节点对，n为D中所有节点对的数目。对于每种预测算法t，计算出预测测试集合D中每一对节点u、v的Suv，然后进行降序排列，选取前m'个节点对，形成集合P'，剩下的形成集合Q'。m'是集合D中实际存在于下一时间的图中的节点对数目。按照式(7)，如果ej∈P'，则ht(ej)=1，反之，若ej∈Q'，ht(ej)=-1。

由式(8)获得每个分类器t对于样本ej的投票总和。对于每个ej，由每个弱分类器t对其进行投票。如果分类器t判定ej在下一时刻图中存在，则ej的权重Wej加上此分类器的投票权重αt。如果分类器t判定ej在下一时刻的图中不存在，则为ej的权重Wej减去此分类器的投票权重αt。在所有分类器对ej投票完成之后，若ej的权重Wej为正，即预测ej会在下一时刻的图中存在。反之，ej的权重Wej为负，则预测ej不会在下一时刻的图中存在。

3 实验结果与讨论

3.1 数据集

给定一个图G=＜V,E＞，对于合作网络，合作关系不存在方向性，将它视为无向图。对于Email-Net，即邮件网络，视作有向图。边e=(u,v)∈E。设Gi代表了在时刻ti到ti'时间段内图G的子图。选取t0＜t0'＜t1＜t1'＜t2＜t2'这几个时间段。将G0和G1作为分类器权重训练的训练集。将G1和G2作为对G1预测在G2上验证的测试集。

本文使用的数据集包括arXiv论文合作网络中4个领域的数据以及一组电子邮件网络数据。其中，论文合作网络的数据使用scrapy爬虫爬取。具体策略如下。

首先选定爬取的文章领域以及文章发表的时间段，爬取该时间段该领域所有文章的链接并将其存储在数据库中。将所有的文章链接标记为未爬取。然后从数据库中选取一定数量的未被爬取的文章链接，对其进行爬取。完成后将此文章链接标记为已爬取。重复爬取过程直到所有的文章链接标记为已爬取。使用Xpath对爬取下来的页面进行解析，获取每篇文章的题目、发表时间以及作者列表，将结果存入到数据库中。

对于爬取下来的作者列表，以Hep-ph为例。将每个作者视为一个节点，如果2个作者出现在同一篇文章的作者列表中，则为这2个节点间生成一条无向边。对这个领域的所有文章的作者列表处理完成后，生成一个这个领域的关系网络。定义t0为1994年，t0'为1996年，t1为1997年，t1'为1999年，t2为2000年，t2'为2002年。所有的图均为无向图。其他3个领域的数据也按同样的方法处理。

本文所使用的邮件通信数据来源于国内某高校的电子邮件服务器日志，从中截取一段时间的数据作为测试数据。该日志包含的内容较为简单，仅有邮件收发地址和邮件发送时间，通过将用户视为节点、通信关系视为边，可以构造出电子邮件用户间的邮件通信关系网络。取3周的邮件数据，第1周数据生成图G0，第2周的数据生成图G1，第 3周的数据生成图G2。所有的图均为有向图。

3.2 实验设计

实验中考虑2种预测情况。第一种预测是预测完全新生成的边，仅对那些在当前图中没有形成边的节点对进行预测。作为弱分类器的预测算法有CN、JC、AA、RWR。为了与Liben-Nowell D相关工作作比较，参照其实验数据设定，本文仅考虑活跃节点的链路预测问题。定义集合A是在G0、G1中度至少为3的节点的集合，集合B是在G1、G2中度至少为3的节点的集合。预测训练集合为C：A×A-E0。预测测试集合是D：B×B-E1。

另一种预测是将节点间在当前时刻已存在边的情况考虑在内的预测，对该时间段的图中节点两两组合所有可能形成的节点对做预测。在这种情况下，如2.2节所述，加入Wuv作为弱分类器，它表示点u、v之间在当前图中已经存在的边的数目。在合作网络中，表示二者在当前时间段已经合作的文章数目。在邮件网络中，表示二者在当前时间段已经发送的邮件数目。作为预测训练的集合是C：A×A，作为预测测试的集合是D：B×B。数据集合如表3所示。

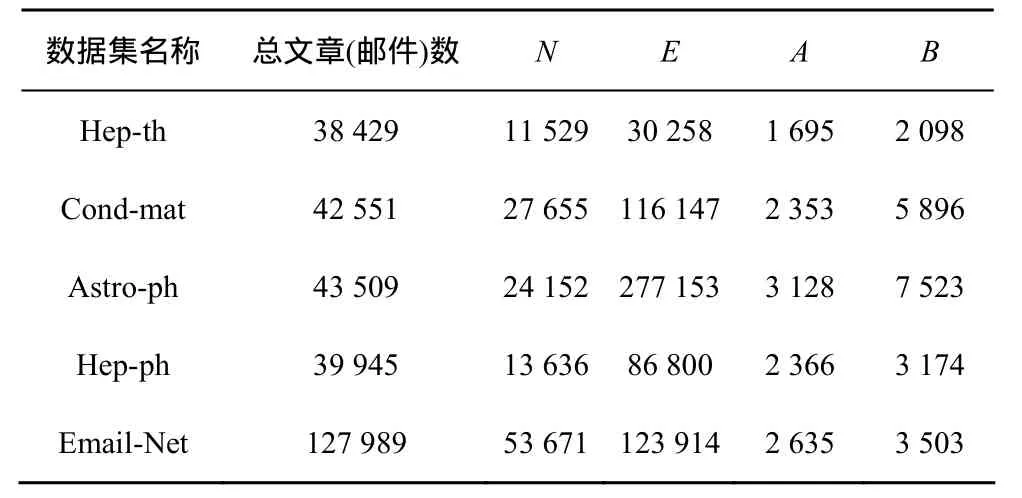
表3 所有的数据集

3.3 实验结果分析

接下来，展示本文提出的算法——ALP（adaBoost link prediction）在每个数据集上的表现，以及它同其他链路预测算法之间的比较。

3.3.1 问题评价方法

用来衡量链路预测算法的精确度指标一般有准确率、召回率和AUC(ROC曲线下的面积) 3种。准确率仅考虑对排在前Mbit的边的预测是否准确。召回率仅考虑对所有标签为真的样本是否被预测为真。两者相对来说评价都比较片面。而 AUC是从整体上来衡量算法的精确度[15]。AUC值同时反映了预测的准确率以及召回率。近年来链路预测工作的评价方法基本采用ROC图和AUC值。

ROC图像是一种对于灵敏度进行描述的功能图像。一个二分类问题的结果要么是真（P），要么是假（N）。假如输出的预测是 P而真实的结果也是 P，那么就叫做真阳性（TP）；但是如果真实的结果是N，就叫做假阳性（FP）。相对来说，一个真阴性发生在预测结果和实际结果都是N的时候，而假阴性是当预测输出是N而实际值是P的时候。TPR决定了一个分类器在所有阳性样本中能正确区分阳性案例的性能，即召回率，由式(9)计算。而FPR决定了在所有阴性的样本中有多少假阳性的判断，由式(10)计算。将假阳性率（FPR）作为x轴，真阳性率（TPR）作为y轴，就生成ROC曲线。每一个预测结果在ROC空间上以一个点代表，一组预测结果就会生成ROC曲线。ROC图上从左下到右上的对角线表示一个完全随机的预测。这条线也叫无识别率线。在这条线以上的点代表了一个好的分类结果，而在这条线以下的点代表了差的分类结果。AUC是ROC曲线的面积。AUC的值越大表示一个分类器的表现越好。本文采用ROC图和AUC值来评测算法的精确度。

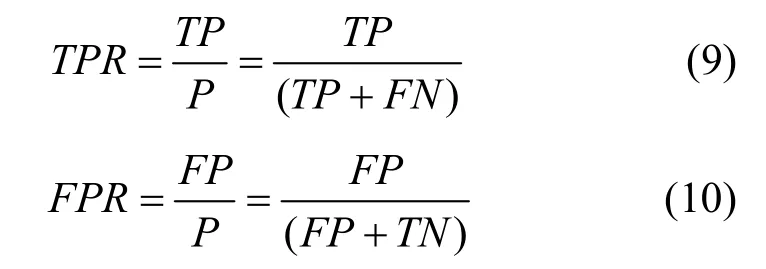
3.3.2 对网络中新出现的边进行预测

该预测仅对那些在当前图中没有形成边的节点对进行预测。观察合作网络的Hep-th领域内的数据表现情况。按上述所说，使用1994～1999年的数据训练出每个分类器的投票权重。在1997～2002年的数据上，对1997～1999年的数据依据之前的投票权重作出预测，在2000～2002年的数据上对预测结果做验证。作为弱分类器的预测算法是 CN、JC、AA、RWR。最后将本文提出算法的预测结果与这几种算法的预测结果做比较。各个算法的表现情况如图3所示。

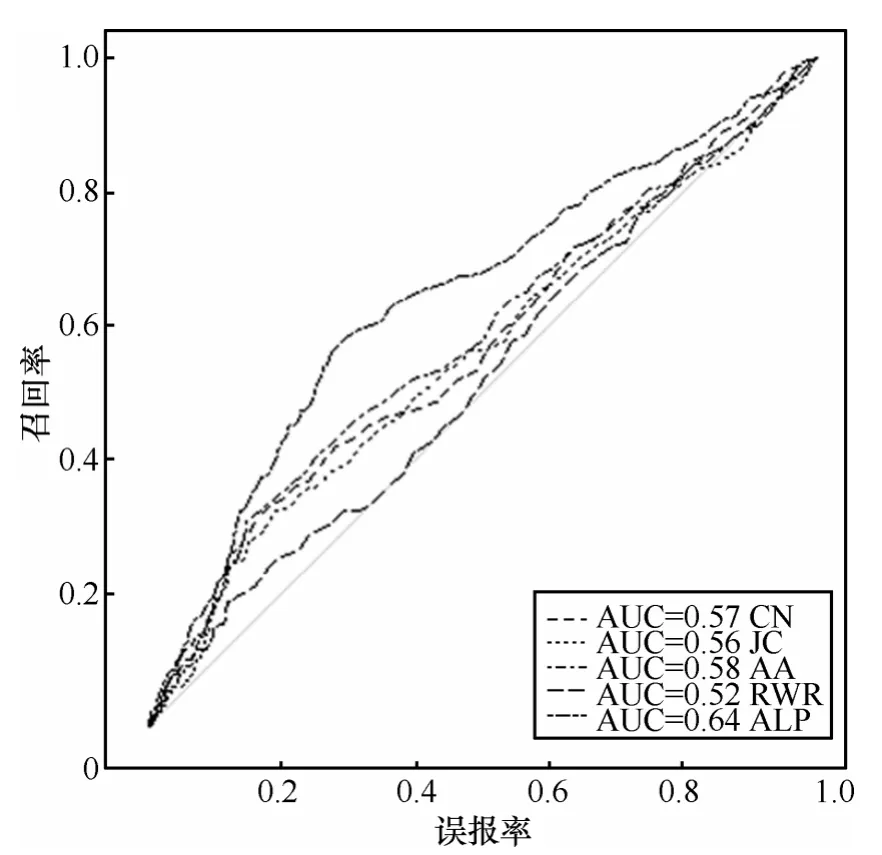
图3 Hep-th 数据集上各算法的ROC曲线(对网络中新出现的边进行预测)

从图3中可以看出，在对Hep-th领域内的数据集做预测时，几乎所有的预测算法曲线都在无识别率线之上。按上节所说，ROC曲线越靠近左上角说明该算法的结果表现越好。可以看出，RWR算法的预测表现最差，几乎贴近无识别率线。算法CN、JC、AA的表现较为接近，它们的ROC曲线离无识别率线均有一定的距离，相对来说预测表现比RWR算法略好。本文所用的基于 AdaBoost的链路预测算法ALP的ROC曲线在其他曲线的上方。且离它们都有一定的距离。由此可见，在对Hep-th领域内的数据做预测时，该算法表现优于其他算法，提高了链路预测的准确率和召回率。对于只预测新生成的边的情况，各个数据集上每个算法的表现情况如表4所示。

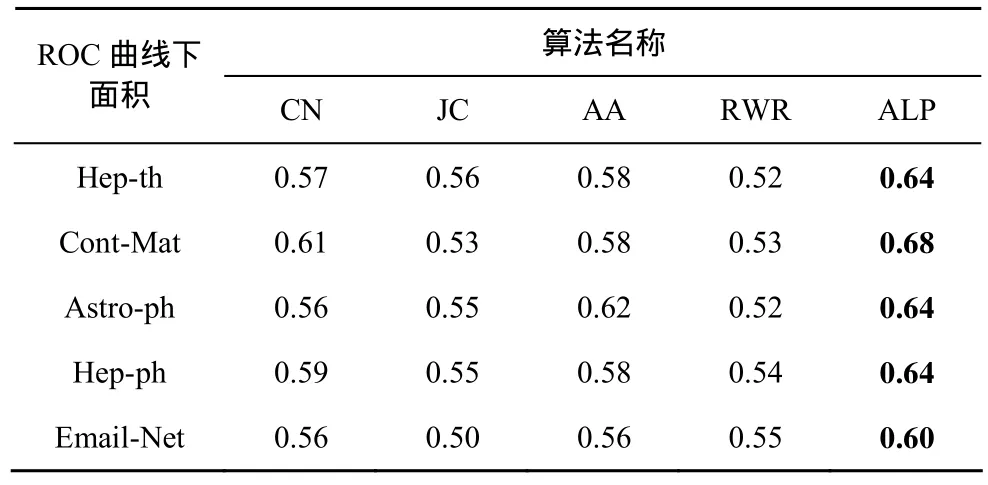
表4 各个算法在5个数据集上的表现(仅对新出现的边进行预测)

从表4中可以看到，对于表中所列的5种预测算法，在实验所用的 5个数据集上。其 AUC值均在随机猜测值 0.5之上，即它们的预测结果都高于随机猜测。本文用作弱分类器的4种算法的表现相差不大。但是CN以及AA方法的AUC值较 JC和 RWR算法略高。而本文提出的算法ALP在合作网络的 Cont-Mat领域数据集上表现最好，在邮件网络上表现较差。但是无论是在论文合作网络还是在电子邮件网络数据集上，它的AUC值均高于其他算法，且存在一定的差值。实验结果表明，该算法在提高了正确预测结果的同时，并没有扩大预测范围，同时提高了链路预测算法的准确度以及召回率。说明本文对于链路预测算法的改进是有效的。

3.3.3 对网络中所有可能存在的边进行预测

该预测是将节点对在当前图中已存在边的情况考虑在内，对该时间段的图中节点两两组合所有可能形成的节点对做预测。笔者同样对合作网络的Hep-th数据集进行测试。按上述所说，使用1994～1999年的数据训练出每个分类器的投票权重。在1997～2002年的数据上，对1997～1999年的数据依据之前的投票权重作出预测，在2000～2002年的数据上对预测结果做验证。作为弱分类器的预测算法是CN、JC、AA、RWR、Wuv。同时这几种算法的预测结果也用来和本文提出的算法 ALP的预测结果比较。各个算法的表现情况如图4所示。

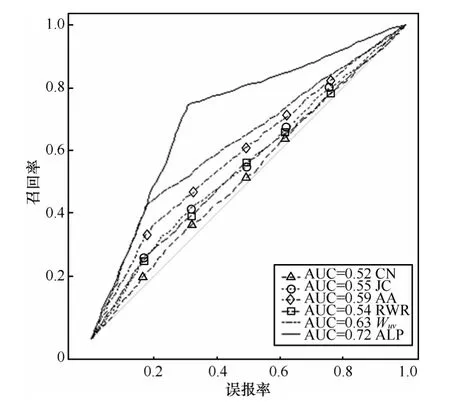
图4 Hep-th数据集上各算法的ROC曲线（对网络中所有可能存在的边进行预测）

从图4中可以看出，在对Hep-th领域内的数据做预测时，所有的预测算法的 ROC曲线都在无识别率线之上。其中，CN的表现相对较差，它的ROC曲线与无识别率线最为贴近。依次往上是算法RWR、JC、AA、Wuv，这几种常用的链路预测算法的 ROC曲线离无识别率线都有一定的距离。但是相互间的间距都不大，没有特别明显的表现差异。图 4最上方的 ROC曲线是本文中提出的基于AdaBoost的链路预测算法ALP，它离无识别率线的距离远远大于其他算法，且离图中的左上方最为接近，可以看出它的预测表现是明显优于其他 5种用于比较的算法。由此可见，在对Hep-th领域内的数据做预测时，该算法表现远优于其他算法，提高了链路预测的准确率和召回率。

各个链路预测算法在本文所用的5个数据集上的表现如表 5所示，当考虑到已有合作或是已存在通信的情况进行链路预测时，在各个数据集上，所有的6种算法的AUC值均大于0.5。说明文中使用的链路预测算法都有一定的预测效果。观察前面 5种用作比较得预测算法，可以看出，它们之间的预测表现得差异不大，算法Wuv的表现相对来说较为良好。在各个数据集上都略高于其他算法。说明作者间已经合作过或是实体间产生过通信对于在以后的时间中继续合作以及继续通信的可能性有很大的影响。本文提出的算法ALP在5个数据集上的AUC值都高于其他用作比较的5种算法。在Hep-th数据集上表现最好。在数据集Astro-ph上表现相对较差。在数据集 Email-Net上的预测效果与在合作网络上的预测效果并无太大差异。说明本文提出的算法ALP具有一定的可适用性。该算法在预测中提高了正确预测结果，并且没有扩大预测范围。显著提高了链路预测算法的准确度以及召回率。说明本文提出的对于链路预测算法的改进是有效的。

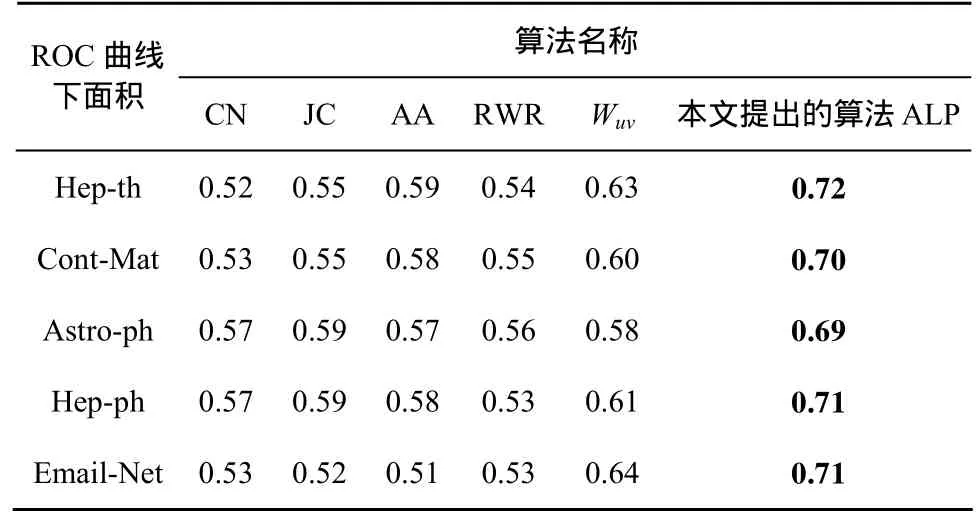
表5 各个数据集上每个算法的表现（对网络中所有可能存在的边进行预测）

该算法的运行时间与所选取的作为弱分类器的链路预测算法有关。在一个处理器为2.5 GB的电脑上运行Hep-th数据的时间约为30 min。

4 结束语

本文提出了一种基于 AdaBoost的链路预测算法。通过在真实的论文合作网络和电子邮件网络数据集上的仿真实验结果表明，本文提出的链路预测算法相对于现有的各种常用算法而言具有更高的灵敏度和更低的误报率，能够在显著提高算法召回率的同时，保持计算结果的正确性。本文的主要贡献是将Boosting算法思想引入到链路预测领域，在以后的工作中，可以选取不同的弱分类器来改进算法，也可以考虑采用其他集成学习方法和手段来设计新型链路预测算法。

[1] LIBEN-NOWELL D, KLEINBERG J. The link-prediction problem for social networks[J]. Journal of the American Society for Information Science and Technology, 2007, 58(7): 1019-1031.

[2] LESKOVEC J, BACKSTROM L, KUMAR R,et al. Microscopic evolution of social networks[A]. Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining[C].Las Vegas, Nevada, USA, 2008.462-470.

[3] MYERS S A, LESKOVEC J. On the convexity of latent social network inference[J]. Threshold, 2010,9:20.

[4] SUN Y, BARBER R, GUPTA M,et al. Co-author relationship prediction in heterogeneous bibliographic networks[A]. Advances in Social Networks Analysis and Mining (ASONAM)[C]. Kaohsiung, 2011.121-128.

[5] LARS BACKSTROM J L. Supervised random walks:predicting and recommending links in social networks[A]. WSDM'11[C]. Hong Kong,China, 2011.635-644.

[6] CLAUSET A, MOORE C, NEWMAN M E J. Hierarchical structure and the prediction of missing links in networks[J]. Nature, 2008,453(7191): 98-101.

[7] LV L Y. Link prediction on complex networks[J]. Journal of University of Electronic Science and Technology of China, 2010, 9: 5-39.

[8] SCHAFER J L, GRAHAM J W. Missing data: our view of the state of the art[J]. Psychol Methods, 2002, 7(2):147-177.

[9] CHOWDHURY G. Introduction to Modern Information Retrieval,Third Edition[M]. Facet Publishing, 2010.

[10] ADAMIC L A, ADAR E. Friends and neighbors on the web[J]. Social Networks, 2003, 25(3): 211-230.

[11] TONG H H, FALOUTSOS C, PAN J Y. Fast random walk with restart and its applications[A]. Proceedings of the ICDM'06[C]. Washington,DC,USA, 2006.613-622.

[12] SHANG M S, LV L, ZENG W,et al. Relevance is more significant than correlation: information filtering on sparse data[J]. Europhys Lett,2009, 88(6): 68008.

[13] POLIKAR R. Ensemble based systems in decision making[J]. IEEE Circuits and Systems Magazine, 2006, 6(3):21-45.

[14] SCHAPIRE R E. The strength of weak learnability[J]. Machine Learning, 1990,5(2):197-227.

[15] BRADLEY A P. The use of the area under the ROC curve in the evaluation of machine learning algorithms[J]. Pattern Recognition,1997, 30(7): 1145-1159.