脉冲状态间隔调制方法及恶劣环境下通信实验

母一宁，王贺，李平，姜会林

(1. 长春理工大学 空间光电技术研究所，吉林 长春 130022；2. 吉林交通职业技术学院 电子系，吉林 长春 130022；3. 长春理工大学 计算机科学技术学院，吉林 长春 130022；4. 长春理工大学 理学院，吉林 长春 130022）

1 引言

激光通信具有通信速率高、频带宽等优点[1]。然而，大气是一种包含固体、气体、液体分子的混合物，俗称气溶胶，所以当调制后的激光信号在大气信道中传输时，该调制信号会被大气信道调制，即大气信道二次调制[2,3]。从微观角度讲，大气信道的二次调制可以分解为大气衰减、大气湍流和大气散射等现象，这些现象影响到调制信号的幅度、相位与频带。所以在无线激光通信的调制解调模型与大气二次调制模型直接相关。目前无线激光通信普遍采用强度调制/直接检测（IM/DD）系统，其基本调制模型为开光键控（OOK），带宽、功率、差错率是衡量一种调制解调性能的重要指标。虽然当今一些学者针对无线激光通信提出了一系列调制方式，比如：PPM、MPPM、DPIM、FDPIM、DP-PIM、DH-PIM、DH-PIM等[4～9]。但是因为大气湍流效应会造成接收功率随机起伏[10]，造成信号误判；大气散射会造成多径效应展宽脉冲[11]，引起码间粘连和码间窜扰。所以大气信道属于一种时变非因果信道，需要根据其信道特性对带宽、功率、差错率这三者进行联合分析，进而制定调制解调模型。

本文首先分析在湍流下差错模型，采用最大似然判决近似计算误码率，从数学的角度论证误码率、误时隙率与误分组率三者之间的关系。接着从香农定理的角度分析大气信道对激光通信系统的干扰模型，在该模型的基础上提出列一种脉冲状态间隔调制编码方式，并且详细论述了该编码结构和带宽需求、功率需求、差错性能这3个指标。最后通过野外恶劣环境的全双工通信实验验证了该调制编码方式的可行性与可靠性。

2 差错通信模型分析

2.1 信道功率误差模型

大气是一种典型的时变非因果系统，其成分、温度、湿度、密度等在小空间和短时间内都是随机变化的，进而是大气信道的折射率也随之变化，这种由大气引入的随机干扰便是大气湍流效应。大气湍流对激光传播的干扰与激光直径和湍流漩涡尺度之比直接相关。当激光直径与湍流尺寸的比值远小于1时会发生光束漂移；当激光直径和湍流涡旋的尺度相当时，湍流涡旋使激光波前发生随机偏折，使到达角随机起伏；当激光直径比湍流涡旋的尺度大得多时会造成光束强度在时间和空间上随机起伏,即所谓的光强闪烁。可见从接收功率角度讲光束漂移、到达角起伏和光强闪烁均会引入噪声功率信号，对于距离在几公里以内的噪声功率可以近似服从对数正态分布，其概率分布函数为

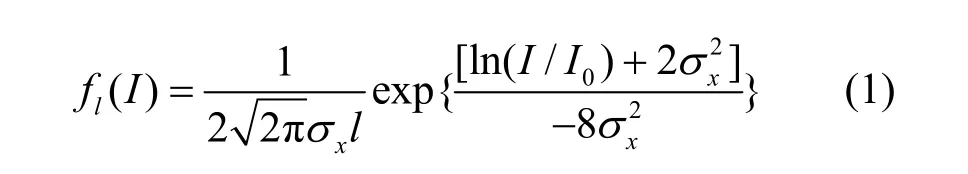
其中，σx为光强闪烁指数，I0为光强的时间平均值，I为接收光强。大气湍流对光波传输影响程度通常用Rytov变量度量，对应于弱起伏平面波的归一化光强起伏方差可表示为

其中，Cn2为折射率结构常数，k为波数(2π/λ)，z为光波的传播距离。传输距离为13 km的CCD探测的光斑平均亮度曲线如图1所示。

背景光噪声可以通过一个高通滤波器将其滤除，光电转换过程与接收机电路引入的噪声服从高斯分布，即引入为加性高斯白噪声。此时的信道等价于大气随机信道与高斯随机信道相互级联。通常情况下调制波形为单极信号。当信号为1时，其时隙信号表达式为ηI+n(t)；当信号为0时，其时隙信号表达式为n(t)，其中，η=γeTegλ/(hc)为光电转换效率，γe为探测量子效率，e为量子电荷，g为光电增益，λ为光波波长，h为普朗克常数，c为光速，T为每个时隙的持续时间。n(t)为加性高斯白噪声Nawng(噪声功率谱密度为nawng)与大气信道噪声Nrand的累加和，其高斯信道下的差错时隙出现概率为Pi，所以级联后的传输错误率为

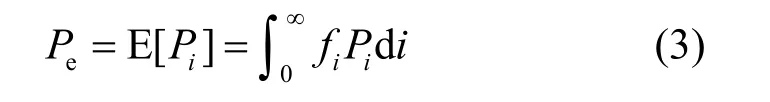
2.2 信道带宽误差模型

激光的波长很短，所以将激光光波作为载波无须考虑载波带宽的问题。由经典香农理论可知

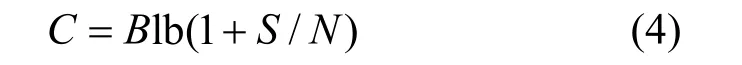
其中，B代表带宽，S代表功率，n为噪声功率谱密度，N代表噪声功率。在无线激光通信中带宽B分别被激光器发射带宽(Bs)、光电检测带宽(Br)和信道传输带宽(Brand)所限制（因为光载波趋近与无穷大所以不加考虑）。相互关系为

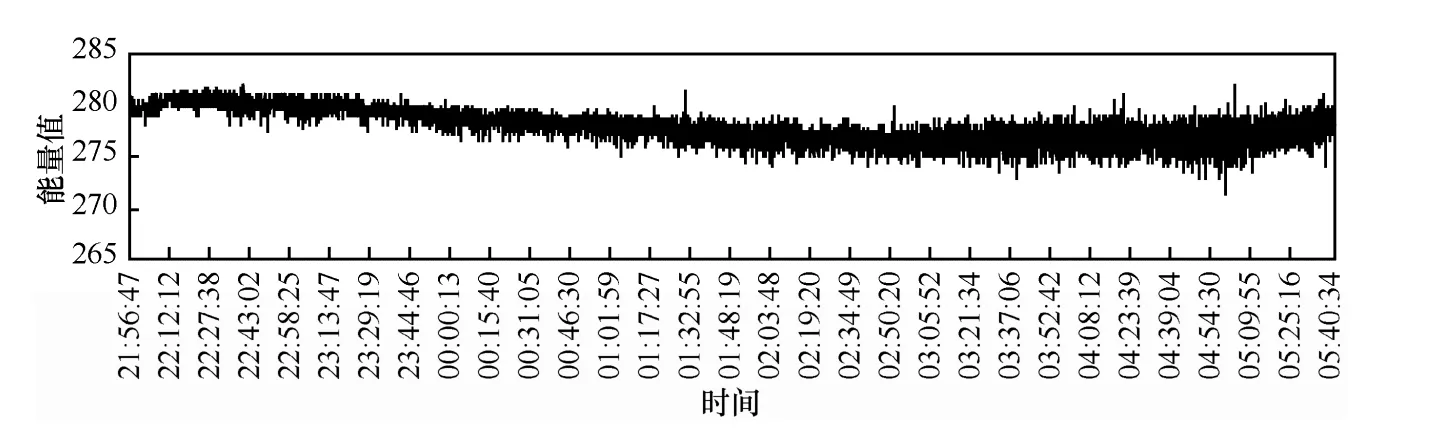
图1 光斑亮度变化曲线

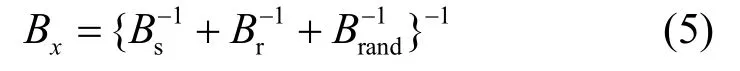
大气对光波的散射效应会改变光子的传播方向，并由于存在多次散射效应，使部分光子到达探测器所经过的时间发生改变（光程不变，路径改变），即激光在大气中传输存在多径效应。可见在实际通信过程中激光器发射带宽和光电检测带宽均是恒定不变的常量，而信道传输带宽是一个随机变量，该变量和天气环境直接相关，即无线激光通信系统的香农极限速率与大气信道环境直接相关，信道带宽对通信带宽的影响是非线性的。

空间无线激光通信（FSO）的香农极限通信速率公式可以改写为

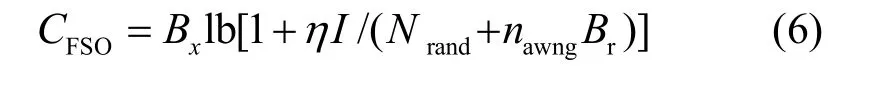
设激光器发射带宽Bs=2 500 MHz，光电检测带宽Br=2 500 MHz，激光接收功率为1 dBm，大气信道引入的光强闪烁噪声Nrand= -10 dBm，接收噪声功率谱密度为nawng=5 pW/MHz，信道传输带宽Brand逐渐降低，其香农极限通信速率变化效果图如图 2所示。同理，设定大气信道带宽恒定在2.5 GHz，大气信道引入光强闪烁噪声逐渐变化，效果图如图 3所示。

图2 信道带宽影响效果

大气信道的变化是不能通用单一的方程式解释的，虽然图2和图3不能完全说明大气信道可通率（因为当大气信道带宽下降的同时，光强闪烁强度也会随之增加），但是图2和图3足以证明大气信道带宽的衰减与大气光强闪烁对激光通信有着相同的抑制作用，所以在确立调制解调模型时应该把功率需求与带宽需求放在同等重要的位置。大气信道带宽的降低直接会对通信引入码间串扰和码间粘连，与调制解调模型的抗差错性能直接相关。

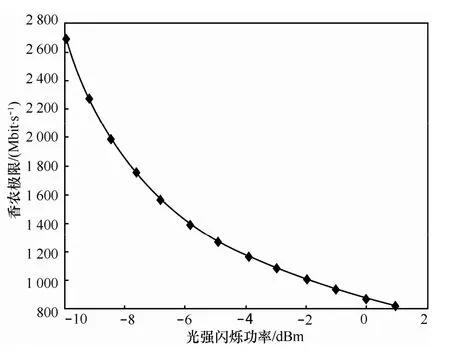
图3 信道功率影响效果

3 PSIM调制概述及相关性能分析

3.1 误码与误分组

从符号结构的角度可以将调制编码分为定长调制与变长调制2大类。最为典型的定长调制编码为 PPM 编码，其符号长度和脉冲数固定，当其调制阶数为M时，其接收到的电流矢量为r= (r0,r1,…,r2M-1)，其各个分量独立统计，假定脉冲出现位置为k∈S{0,1,…,2M-1}时，只有rk＞ max(rj|∈S,j≠k)时才能正常判决，令Aj={rj＜rk,j≠k|r}，符号可以正常判决的概率为A∩Aj，其中，Aj事件均互相独立，A为时钟提取正确几率，误分组率为

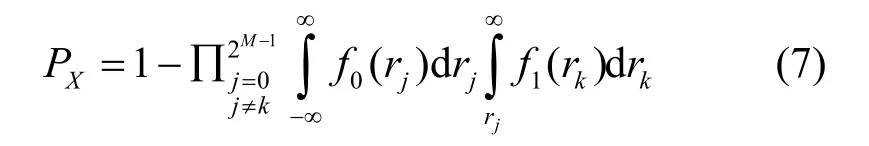
2个积分函数分别为不同时隙电平的电流概率密度，PPM的误符号率的近似表达式为

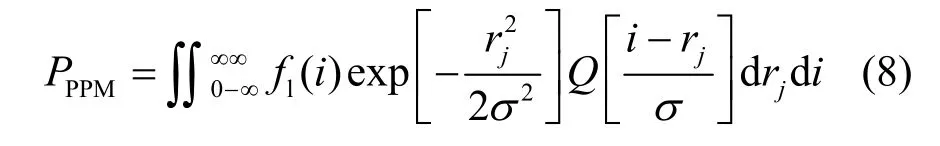
单个符号内发生误判是会同时产生2个时隙误差，所以其时隙误差为[1/(2M-1)]PPPM。错误的符号经过解调后仍会产生部分正确信息，因为在调制前各个码字具有相同的先验概率，其错误概率只能发生在接收译码端，所以PPM平均误比特率为

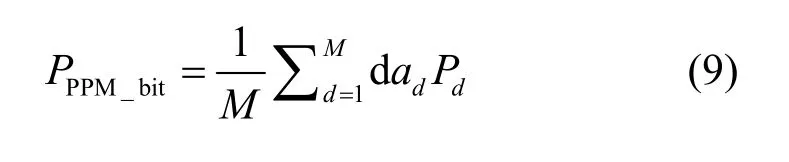
式(9)中的Pd为发送全零码字时，解调出汉明码重为d的码字出现概率，其中，ad是汉明重为d的码字个数。脉冲出错位置为

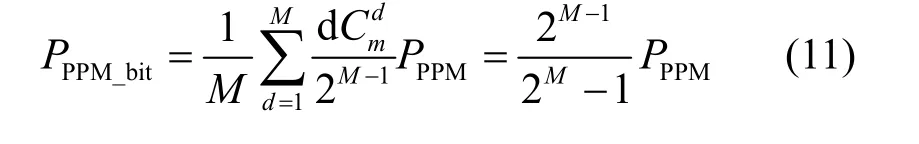
可见这种以 PPM 为代表的定长编码性能主要受调制阶数、大气闪烁强度、平均接收光强及噪声影响。当调制阶数为一阶时，其误比特率和符号率相同，但调制阶数逐渐增大时，误比特率变化与误符号率相似, 但误时隙率则较为平稳。但是以DPIM为代表的变长调制方式，由于符号内时隙个数不定，所以当出现时隙误判时，不仅会影响当前符号，并且会使后续符号均发生错误。进而导致非定长调制编码的误码率高于理论计算的误分组率[12]。

3.2 PSIM符号结构与特点

因为不同调制方法的符号结构各不相同，所以不同种类调制方法的性能特性也有所不同，其中性能特性主要包括功率需求、带宽需求、差错能力等。以 OOK为例，输出高功率激光表示为比特“1”，输出低功率激光表示为比特“0”，用带宽BOOK来表述OOK在传递信息时比特“1”可能出现的频率范围。但采用二进制OOK调制方式传输2X数据时，其频谱带宽BOOK为0～XHz（0 Hz特指连零情况，XHz特指“1”和“0”等间隔出现）。

在调制编码中，设每 2次“1”出现的时间间隔为T，即1/T便是“1”出现的频率fx，其中，“1”出现的时间与总时间T的比为占空比。脉冲出现频率fx的不确定度可以实现信息的传输，例如，PPM根据脉冲出现位置不确定度传递信息，DPIM 根据脉冲间隔不确定度传递信息。但是通过fx的不确定度传递信息。但仅仅靠脉冲之间不确定度传递信息，其带宽利用率必然很低。

脉冲状态间隔调制编码方法则是通过根据脉冲间隔不确定度和不同脉冲间隔出现状态不确定度联合传递信息。以四进制脉冲状态间隔调制编码为例，设四进制PSIM编码拥有5种脉冲时间间隔，分别为T1、T2、T3、T4和Tx，其中，Tx为同步间隔T1、T2、T3、T4为信息间隔，设定每组符号有4组脉冲信息位，每组符号位可以传输8 bit。具体符号编码的组合方式为首先出现时钟同步时隙Tx，然后在Tx的后面为4个信息时隙，根据这4个信息时隙的绝对组合方式获得该符号的信息值。其中，T1、T2、T3、T4这4种时间间隔可以是等变长间隔也可以是渐变长间隔，设时钟同步时隙和最小步进时隙均为Tx，信息间隔时隙表达式为

其中，当a=1时为等变长PSIM编码；当a取值范围为0～1时为渐变长PSIM编码。

四键控渐变长PSIM符号结构如图4所示，该图为可编程逻辑门阵列(FPGA)仿真环境下实际符号结构图。由图可见该符号可以传输32 bit信息。

3.3 性能分析

功率需求与带宽利用率是评价通信模型的2个重要指标，并且这2个指标直接影响该调制方式的抗差错能力，在此分析OOK、PPM、等变长PSIM、渐变长PSIM这4种调制方式在不同键控进制下的功率需求与带宽利用率以及抗差错能力。

从调制表达式的角度对比，在相同误码率条件下，不同调制方式的功率需。本文将带宽利用率定义为

其中，R为数据速率，B为通频带宽，M为信息比特分组长度，n为与M信息比特时间内划分的脉冲位置数，因为ηOOK=B/R=1，所以本文对OOK频带利用率做归一化处理，用其他频带利用率与ηOOK做比较，进而评价带宽利用率的高低程度。设 OOK调制编码的码速为Rb，在相同码速率下，PPM和DPIM带宽需求量为

图4 PSIM符号结构

在相同码速率下，PSIM带宽需求量为

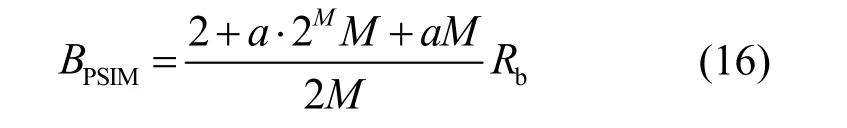
由图5可知，PSIM调制编码的带宽利用率均高于其他编码方式，仅仅低于OOK调制方式。

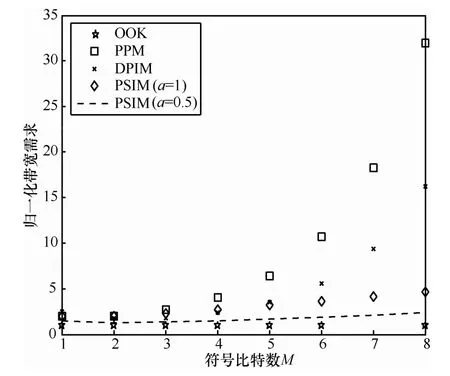
图5 开关键控、脉冲位置调整、脉冲间隔调制、脉冲状态间隔调制带宽对比

同理在对比功率需求时依然对OOK调制的功率需求做归一化处理，在相同码速率下，PPM 和DPIM功率需求为

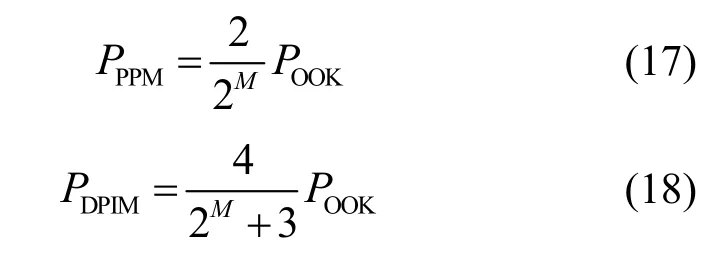
在相同码速率下，PSIM功率需求量为

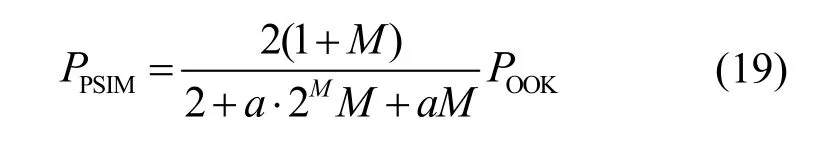
由图6可知，PSIM调制编码的功率需求优于其他编码方式，仅略低于PPM编码方式，当a=0.5时其功率需求较高，但随着键控阶数的增加，功率需求逐渐降低。由图5和图6可知，PSIM的信道利用率和功率需求这2个指标的性能均非常优异，唯有渐变式PSIM的功率需求较高，以至于在低阶次键控（M小于4）调制时这种调制方式不具有可行性，但随着键控阶数增加，这种编码方式的优势便体现出来了，当M不小于4以后，渐变式PSIM编码的高带宽利用率和低功率需求的特点便体现出来，因为在恶劣环境下信道带宽衰减得十分明显，所以本文后续再浓雾环境下进行的野外通信实验就是采有M=4，a=0.5的渐变式PSIM调制模型。

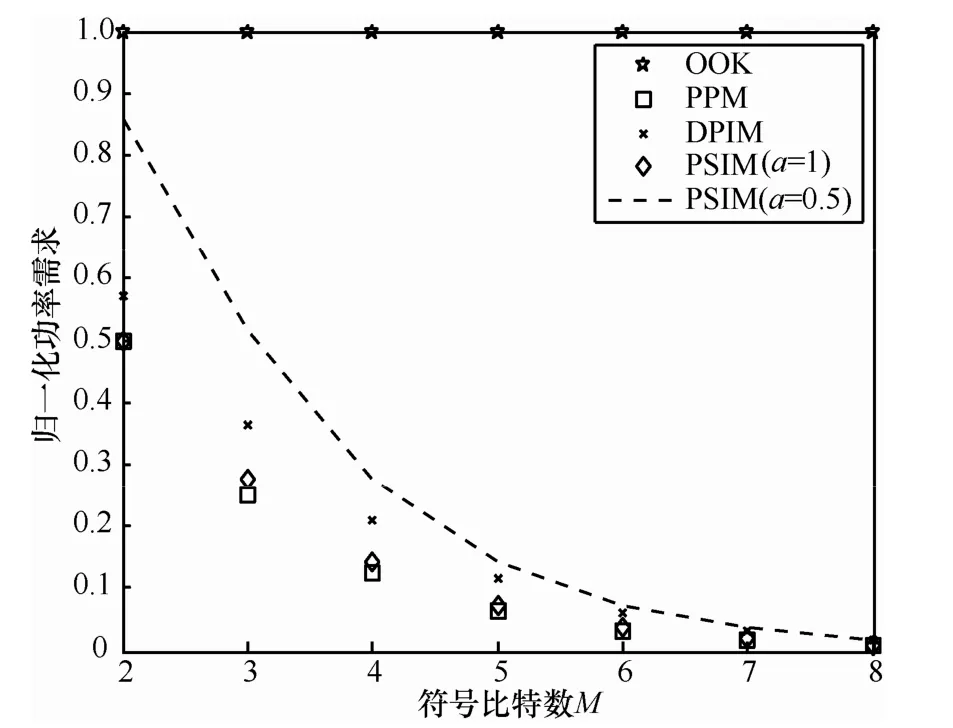
图6 开关键控、脉冲位置调整、脉冲间隔调制、脉冲状态间隔调制功率对比

衡量调制解调模型的抗差错能力可以直接比较不同调制模型星图中的最小欧几里得距离，最小欧几里得距离与误码率之间的关系为

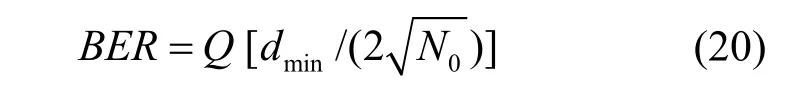
其中，dmin是不同调制码元结构之间的最小欧几里德距离，N0为噪声功率谱密度。最小欧几里得距离的表达式为

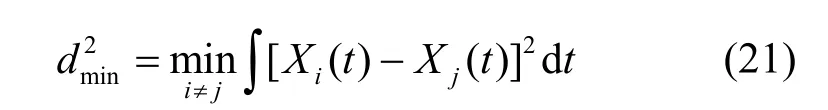
其中，X(t)表示输入为不同码元结构所对应的调制波形。

当大气信道变化时，不仅大气的多径效应会随之变化，而且相应的湍流闪烁效应也会随之增强，所以单独对大气的脉冲展宽模型和光强闪烁模型进行误码率仿真是不足以反映该调制编码在真实的通信情况下的误码性能[6]的。所以通过比较不同编码方式最小欧几里德距离的长短粗略评价编码方式的抗差错能力，最后通过在恶劣气候环境下的野外通信实验验证其可行性。设P为平均功率，Rb为传输速率，即Rb=1/τ，由于在传输信息时 OOK调制中高低电平等间隔出现，所以OOK脉冲的峰值功率为2P，即最小欧几里得距离为

同理可求PPM调制、DPIM调制、PSIM调制的最小欧几里德距离为

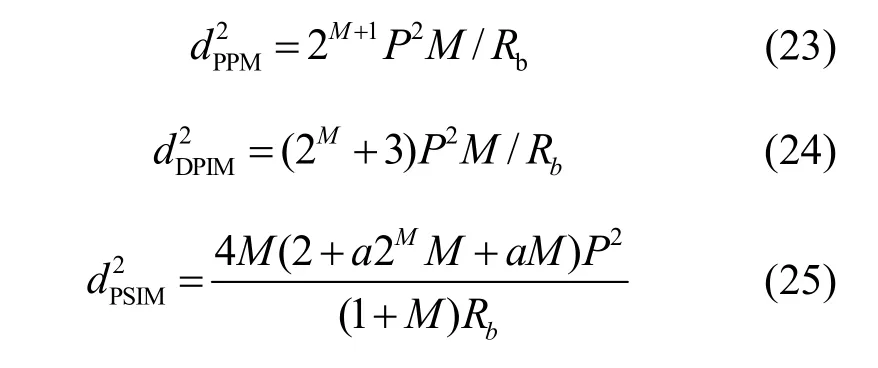
假定上述 4种方法采用相同的激光平均功率和相同的传输速率，最小欧几里德对应如图7所示。

图7 最小欧式距离变化趋势对比

可见，在相同的平均功率和相同传输带宽时，PSIM具有优良的抗差错能力。

4 恶劣环境PSIM通信实验

为了提高环境对PSIM调制模型的影响，所以本系统并未采用大气窗口的通信波长进行通信，而是采用易受大气信道影响的658 nm波段进行通信，该激光器连续输出功率为18 dBm，发散角为0.8 mrad，接收口径为80 mm透射式光学天线，由于通信光属于准单色光，所以只需要对该系统校整球差，无需校整色差，光电探测器选择PIN接收管。PIN探测器前置窄带滤光片。具体光学接收天线如图8所示，整体系统结构如图9所示。

2012年9月1日下午13时～17时，在长春净月潭国家森林公园展开了浓雾环境下2 km野外无线激光通信实验，由于当天大雾弥江，能见度不足500 m，以至于光轴自动对准系统完全失效果，改用手动进行光轴调整，采用全反射角锥棱镜作为第三方合作目标实现光轴对准。

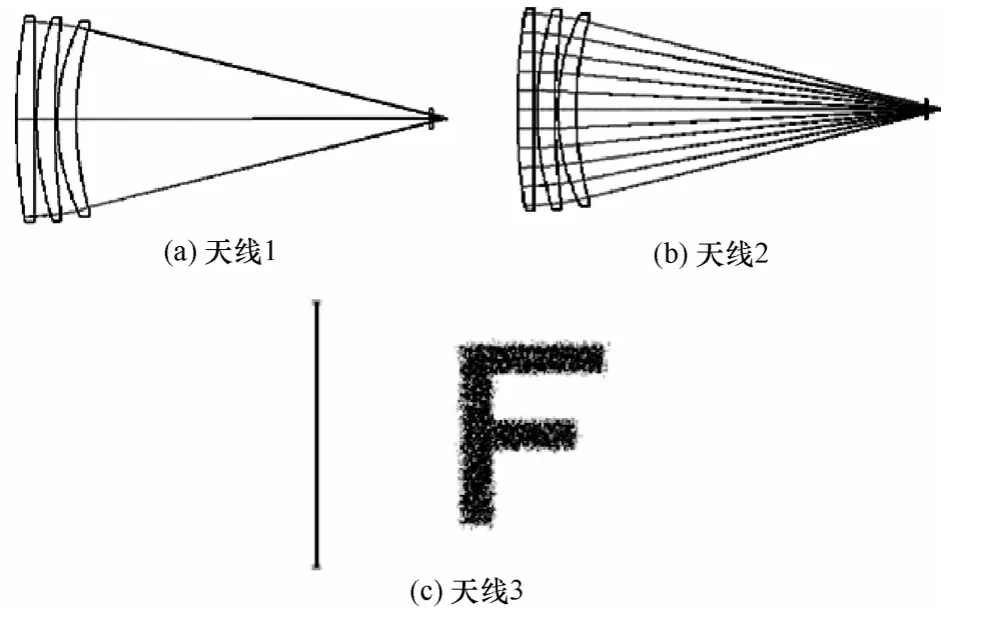
图8 光学天线

系统采用 USB总线控制数据流速率，通过Visual C++编写MFC上位机控制程序，最终实现USB通信速率连续可调，发送固定txt文件通过对比前后数据计算误码率。底层采用PSIM调制解调模型。

当M=4时，时序基准频率为50 MHz，a=1时，其时隙频率出现范围为[50 MHz, 2.94 MHz]，上位机以8 Mbit/s的通信速率进行通信（将上位机作为数据源通信速率较低，所以每发送一个符号后会有一段空闲期），传输数据量为50 Mbyte txt文件，即13 107 200个符号。通信完成后有7个符号发生错误。

当M=4，时序基准频率为16.6 MHz，a=0.5时，其时隙频率出现范围为[16.6 MHz, 1.85 MHz]，上位机以8 Mbit/s的通信速率进行通信，传输数据量为50 Mbyte txt文件，即13 107 200个符号。通信完成后未有符号发生错误。可见，PSIM 在恶劣大气环境下具有通信的可行性，并且大气信道带宽对激光通信影响十分明显。

5 结束语

首先从工程应用的角度分析了无线激光通信模型，通过研究大气信道模型和经典香农理论指出大气信道带宽是直接影响激光通信的重要技术参数，为了降低激光通信对信道带宽的需求，本文提出一种高效率的脉冲状态间隔调制方式，采用脉冲间隔和脉冲间隔的状态联合传递信息，并且分析了该调制编码方式的特性。最后通过恶劣环境下的无线激光通信实验验证该调制编码方式具有通信的可行性和大气信道带宽对激光通信的重要性。

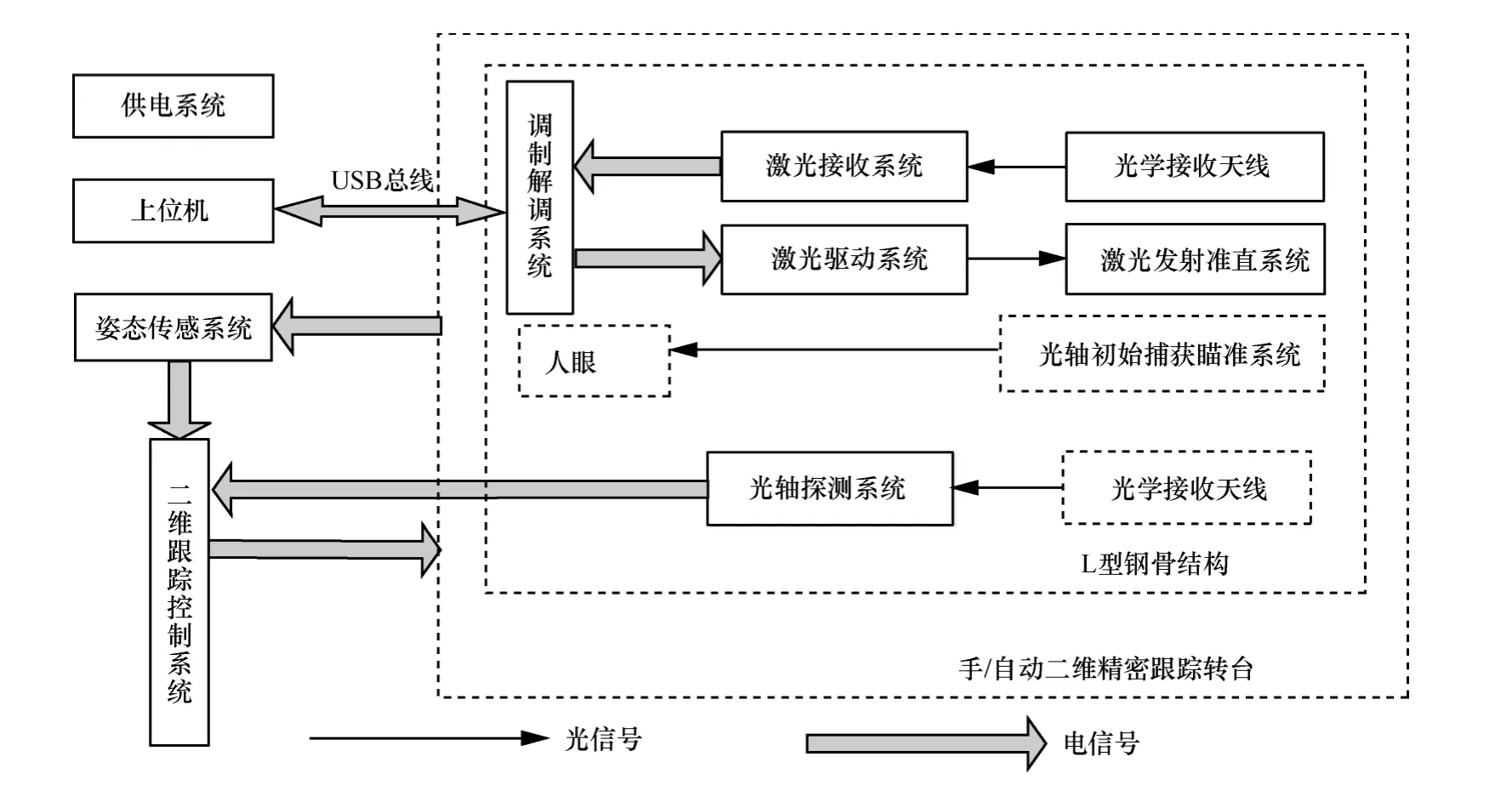
图9 光端机结构

从式(12)可以看出，该编码方式的具有脉冲渐变特性，即a变小时其通信速率增加抗信道影响能力降低，所以大气信道带宽的实时反馈探测技术将是下一步的研究目标，如果可以实现大气信道带宽的实时反馈，便可以根据大气信道情况实时改变通信速率实现“最优激光通信”，为全天候大气无线激光通信奠定基础。

[1] 姜会林, 佟首峰, 宋路等. 空间激光通信技术与系统[M]. 北京: 国防工业出版社, 2011.JIANG H L, TONG S F, SONG L,et al. The System and Technology of the Free Space Laser Communications[M]. Beijing: National Defense Industry Press, 2011.

[2] 母一宁，刘泉，于林韬. 哈特曼技术在序列光斑检测中的应用[J].光学精密工程, 2011, 19(9):2197-2204.MU Y N, LIU Q, YU L T. Application of hartmann technigue in sequence spot detection[J]. Optics and Precision Engineering, 2011,19(9):2197-2204.

[3] 母一宁, 温冠宇, 王贺. 基于序列信息圆心拟合的大气激光光斑检测技术[J]. 空军工程大学学报, 2011, 12(1):59-62.MU Y N,WEN G Y, WANG H. Study of technique of spot detection based on sequence information fit circle center[J]. Journal of Air Force Engineering University, 2011, 12(1):59-62.

[4] ZHU N, ZHU J, ZHONG Q D. The transmission performance of the MPPM modulation in indoor optical wireless communication based on white LED[A]. Proc Asia-Pacific Optical Communication (APOC)[C].Hangzhou, China, 2008. 1-11.

[5] GHASSEMLOOY Z, HAYES A R, SEED N L,et al. Digital pulse interval modulation for optical communications[J]. IEEE Communications Magazine, 1998, 36(12):95-99.

[6] 张铁英, 王红星, 程刚等. 无线光通信中的定长数字脉冲间隔调制[J]. 中国激光, 2007, 34(12):1655-1659.ZHANG T Y, WANG H X, CHENG G ,et al. A novel fixed length digit al pulse interval modulation for optical wireless communications[J]. Chinese Journal of Lasers, 2007,

[7] SH(IU) :DS, KAH.N J M. Differential pulse-position modulation for power efficient optical communication[J]. IEEE Transactions on Communications, 1999, 47(8):1201-1210.

[8] ALDIBBIAT N M, GHASSEMLOOY Z, CLAUGHLIN R M.Performance of du al header pulse interval modulation for optical wireless communication systems[A]. SPIE[C]. Sheffield, UK, 2001.communication systems[A]. SPIE[C]. Sheffield, UK, 2001. 144-152.

[9] 张凯, 张海涛, 巩马理等. 红外双幅度脉冲间隔调制通信系统性能分析[J]. 红外与毫米波学报, 2003, 22(6):411-414.ZHANG K, ZHANG H T, GONG M L,et al. Performance of dual-amplitude pulse interval modulation for wireless infrared communications[J]. Journal of Infrared and Millimeter Waves, 2003,22(6): 411-414.

[10] YUKSEL H. Studies of the Effects of Atmospheric Turbulence on Free Space Optical Communication[D]. Maryland, USA: the University of Maryland, 2005.34-51.

[11] DANIEL V H, DONALD D D. Optimized link model for optical communications through clouds[A]. SPIE[C]. London, UK, 2004.

[12] 胡昊,王红星, 周旻等. 湍流大气中脉冲位置调制和数字脉冲间隔调制差错性能的建模与分析[J]. 中国激光, 2010, 37(5):1269-1274.HU H, WANG H X, ZHOU M,et al. Modeling and analyzing for error performance for pulse position modulation and digital pulse interval modulation under turbulence[J]. Chinese Journal of Laser, 2010, 37(5):1269-1274.