无线传感器网络中带复杂联盟的自适应任务分配算法

郭文忠，苏金树，陈澄宇，陈国龙

(1. 国防科学技术大学 计算机学院，湖南 长沙 410073；2. 福州大学 数学与计算机科学学院，福建 福州 350108)

1 引言

无线传感器网络（WSN, wireless sensor network）作为一种新型的计算模式，它通过在目标区域中部署大量微型无线传感器，以自主组网方式实现大范围内的信息自动采集与处理，具有低成本、高可靠、长周期和抗损毁等优点，有着广阔的应用空间[1]。

由于无线传感器网络中单个节点的能量以及计算和存储能力有限，往往不能独立完成面临的计算任务，需要多个传感器节点采用一定的算法通过交换信息协作完成指定任务。例如，在对象跟踪应用中，为了估计目标的位置，需要进行信号检测、因式分解以及快速傅里叶变换等复杂的数据处理，但是单个节点的计算能力和能量不足以完成这些计算密集型的任务，需要多个节点协同计算移动目标的位置或对多个目标进行分类。又如，在视频传感器应用中，多媒体信息处理通常也都是计算密集型的任务，单个节点的能量以及计算和存储能力无法完成，同样需要多个节点联合处理完成任务[2]。

动态联盟是为了完成特定任务而建立的盟主组织，联盟内的盟主实行资源共享和任务分担，相互合作以期用最佳方式完成任务，使联盟的整体资源得到充分利用，并能保证无线传感器网络任务调度中各个基本任务的服务质量要求。为了适应无线传感器网络拓扑的动态变化、网络和节点资源的局限性以及脆弱的网络环境3个关键特点，本文基于动态联盟思想，很好地将无线传感器网络中任务调度的联盟并行生成机制和自适应调整机制结合，构建了一个基于联盟机制的高度灵活任务调度策略。

2 相关工作

目前，虽然传统网络环境下的任务调度取得了令人满意的成果，但都是假设处理器之间不存在通信冲突，并且几乎不存在能源限制问题。然而，无线传感器网络通信资源受限，传感器节点之间可能存在通信冲突，因此，现有的传统方法难以有效解决无线传感器网络的任务调度问题。

无线传感器网络本身所具有的特性要求任务调度需要从实时性、经济性、节能性和动态协调性等方面改善和满足无线传感器网络对系统性能的要求。文献[2]同时考虑了应用的实时性和网络的能源有效性，提出了一种基于遗传算法 (GA, genetic algorithm)的嵌套优化技术，并在多跳聚簇网络中进行能源高效的任务分配，但该算法在执行的过程中默认网络中传感器节点是同构的；文献[3]基于同构单跳网络环境，设计了一个用于求解任务分配问题的带整数线性规划的多项式时间三阶段启发式算法；文献[4]引入了动态电压调制策略(DVS,dynamic voltage scaling)，提出了一种局部跨层实时的任务映射和调度方案；文献[5]在文献[4]基础上提出了一个基于独立于应用的动态关键路径的任务映射和调度(DCTMP，dynamic critical-path task mapping and scheduling)方案；文献[6]将无线传感器网络任务分配问题抽象为二次0-1规划问题，给出了分布式逐层优化分配算法；文献[7]针对任务在各执行器的协作问题，提出一种动态调度策略，根据执行器节点的剩余能量和工作状态，利用混合模拟退火的粒子群优化(PSO，particle swarm optimization)算法，在任务时效期内统一安排各任务在执行器上的执行周期；文献[8]针对传统的多处理器有向无环图(DAG，directed acyclic graph)调度算法的不足，考虑了能耗和负载平衡2个目标，提出了一种基于GA的任务调度算法；文献[9]同时考虑群间和群内任务分配的合理性，提出了基于可分负载理论的任务最优调度双层规划模型，并利用罚函数原理将线性双层规划转化为目标函数带惩罚项的单层问题进行求解，很好地最小化任务的完成时间和减少节点能耗；文献[10]以空中目标跟踪为背景，针对无线传感器网络协同信息处理中的任务分配问题，提出一种基于最小能量准则的非全连接的环形结构的弹性神经网络模型，解决了多目标跟踪的任务分配问题及多动态联盟对资源竞争冲突时能耗增加的问题；文献[11]基于动态联盟机制，引入联盟覆盖范围和休眠联盟的概念，提出一种带有休眠联盟的动态更新联盟机制，节省了网络资源能耗；文献[12]为延长网络的生命周期，通过平衡所有节点的能量消耗给出了一种能量感知的无线传感器网络任务分配算法。

现有的大部分研究工作仅仅停留在无线传感器网络的静态分配上，虽然有些工作考虑到动态性并提出了一些动态任务分配算法，但大多在任务分配的初始阶段就设定了节点及网络的状态，并没有真正结合无线传感器网络的动态性，来设计真正适用于无线传感器网络的任务分配算法。文献[13]引入动态联盟机制，给出了无线传感器网络任务分配的动态联盟模型及其相应的求解算法，继而采用多agent技术，将动态联盟机制和自适应调整机制相结合，设计了一个基于多agent的无线传感器网络自适应任务调度策略[14]。但该模型只涉及到动态联盟的串行联盟机制，并没有考虑并发的多任务分配和任务截止期的约束。本文基于动态联盟机制，设计了一个无线传感器网络的自适应任务分配算法。算法根据任务截止期赋予任务优先级，优先考虑高优先级任务，对截止期较为紧迫的任务，采用历史信息生成历史联盟，并执行快速子任务分配算法，而对截止期较为宽裕的任务，在满足任务截止期约束条件下，以节点能耗和网络能量分布平衡为优化目标定义适应度函数，设计了一种离散粒子群优化算法，以并行生成联盟，并执行基于负载和能量平衡的子任务分配算法。

3 问题描述

3.1 WSN任务分配问题

考虑一个无线传感器网络由n个异构传感器组成，有m个独立任务要竞争使用传感器，假定该无线传感器网络为一个软实时系统，即在一定范围内允许调度失败而不引起任何灾难性后果，同时截止期未得到保证的任务不予调度执行以避免不必要的能量损耗，则任务分配的目标就是要把这m个任务合理地分配到n个传感器上执行，在尽可能满足任务截止期约束的前提下，优化网络的能耗，均衡网络的负载，并延长网络的生命周期。

根据实际需求，每个任务可以分解为多个不同的子任务，子任务是传感器节点执行的基本单位，最多可达到l个，汇聚节点（sink）实时感知任务并分解成不同需求的子任务，具体的任务需求可由一个m×l的矩阵REQ来表示，其中的元素reqij表示任务i的第j个子任务需求。此外，用一个n维向量E表示节点能量，ei表示第i个节点的能量，并采用一个n×l的矩阵B来表示不同节点对不同子任务的处理能力，元素bi,j表示第i个节点处理第j个子任务的能力，任务的截止期则用一个向量D来表示，元素di可表示为第i个任务的截止时间，另用一个矩阵A表示执行具体子任务的传感器节点，元素aij表示执行第i个任务中第j个子任务的传感器编号，那么可以采用式(1)表示任务i是否错失截止期，若Gapi值为0，则表示按期完成，否则Gapi值为超过截止期的时间。

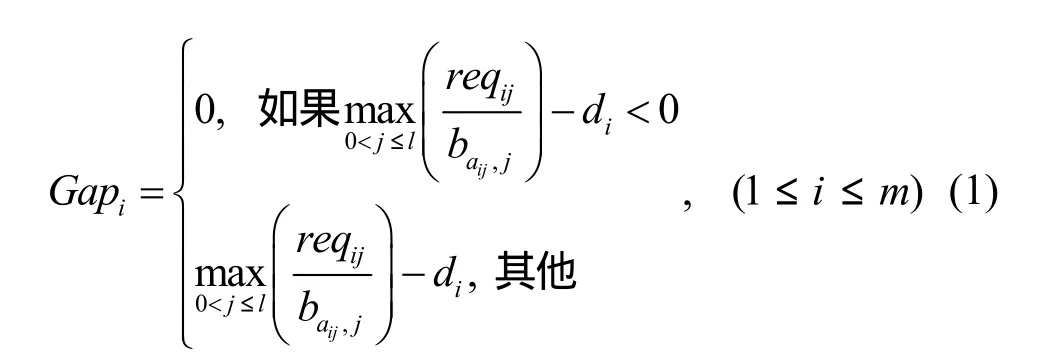
传感器在处理任务i的计算能量消耗具体表示如下

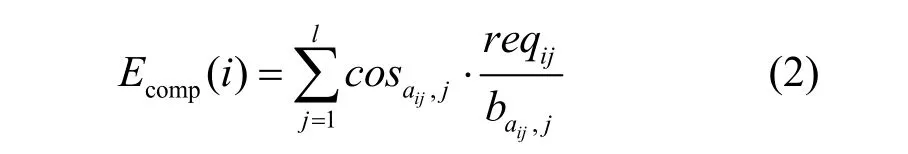
其中，cosi,j是一个n×l矩阵中的元素，表示节点i执行子任务j的单位计算能耗。

传感器在处理任务i的过程中进行调度的必要通信开销如下

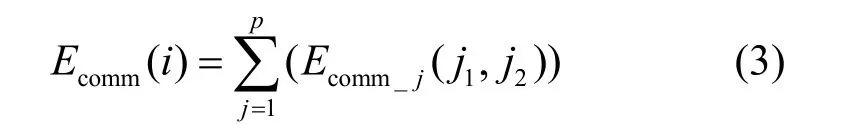
其中，p表示当前任务需要的通信对数，j1与j2分别代表通信两端的节点编号，Ecomm_j表示第j对通信时的能耗，采用文献[15]中的一阶无线模型。

m个任务的总通信能耗EP和当前所有节点的平均能耗AVGEP分别为

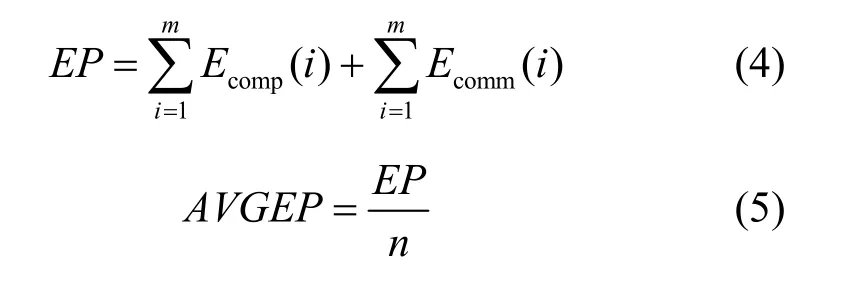
能量分布平衡度是衡量传感器网络的能量分布的平衡程度，其值越小则能量分布平衡越好，从而传感器网络的负载平衡越好，可定义为

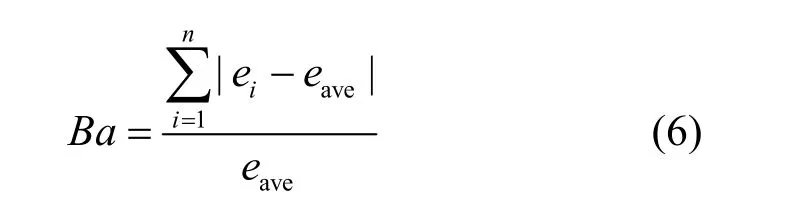
其中，ei为第i个节点的能量，eave是网络所有节点的平均能量。

3.2 动态联盟模型的构造

动态联盟作为多 agent系统中的最为重要协同合作方式之一，它主要通过发挥联盟内各成员的优势或者核心能力，以更高效地完成任务。多任务联盟和交叉联盟是目前复杂联盟的2种主要形式[16]，鉴于动态联盟需要 agent之间反复通信协商以及无线传感器网络节点能量受限，本文设计了一种交叉联盟模型，该模型中一个任务映射一个联盟，每个节点可以加入多个联盟，同一个联盟内的节点需相互合作共同完成任务，联盟由汇聚节点强制生成，无需成员节点多余的协商与交流且不采用联盟最终确认的机制。将该模型运用于传感器网络节点动态组合的研究当中，则传感器在处理任务i的计算能量消耗和通信开销的式(2)和式(3)更新为

从而，无线传感器网络任务分配的动态联盟可抽象为以下多目标优化问题

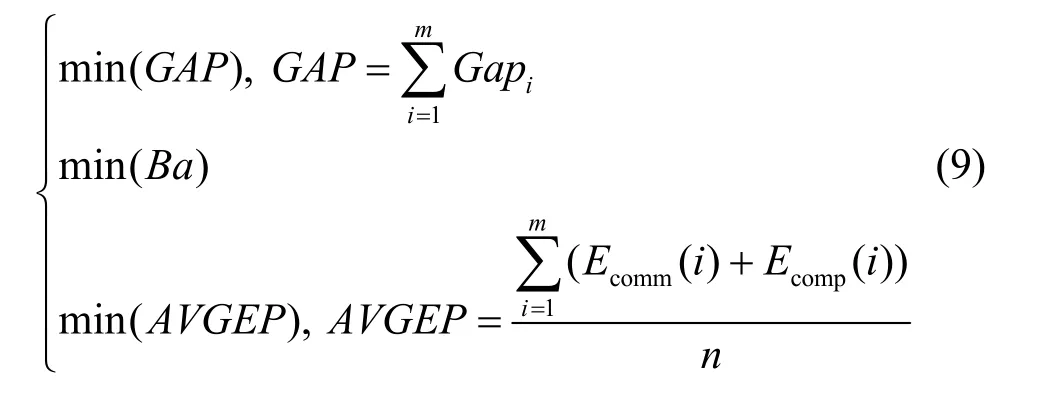
4 算法实现

4.1 自适应任务分配算法的体系结构

最早截止期优先(EDF, earliest deadline first)算法作为最为重要的动态优先级算法之一，已被证明是最佳的动态优先级算法[17]。在系统运行时，汇聚节点利用EDF思想，对感知到的任务按照截止期非减排序，并按与截止期成反比方式设置优先级，即截止期最早的任务拥有最高的优先级，进而以优先级为顺序，分别对每一个任务生成相应的联盟，并在联盟环境下，执行子任务分配算法，最后通过汇聚节点发布任务。当传感器节点收到汇聚节点的指示后，则以子任务所对应任务的优先级为先后顺序执行接收到的各子任务，并向汇聚节点汇报子任务执行状况。而当任务完成后，为避免不必要的能量消耗，汇聚节点解散联盟，释放网络资源，让其余任务顺利得到分配。与此同时，汇聚节点通过维持一个历史联盟信息(HCI, historical coalition information)的阈值，采用先进先出的策略对接收到的HCI进行更新，具体的分配策略如图1所示。

图 1中的联盟生成问题本身是一个 NP难的组合优化问题，要生成一个较好的联盟是一项复杂困难的工作。与其他进化算法相比，PSO算法具有简单实现和更强的全局优化能力的优势，并已经成功解决许多领域中的优化问题[14,18～20]。无线传感器网络中节点部署、节点定位、能量有效分簇、数据融合以及拓扑控制等问题都可抽象为相应的优化问题，文献[21]很好地综述了PSO算法在上述领域的具体应用情况。为很好地解决本文 WSN任务分配中的并行联盟生成问题，需要选用PSO算法并行生成复杂联盟。鉴于PSO在求解联盟生成问题中的算法开销，显然不适合在不同场合下无条件使用PSO算法并行生成联盟，这也无法满足实时性较强任务的时间约束。为此，本文定义了一个时间阈值T0来判断任务截止期的紧迫程度，T0主要取决于PSO算法的时间开销，T0的估值公式为

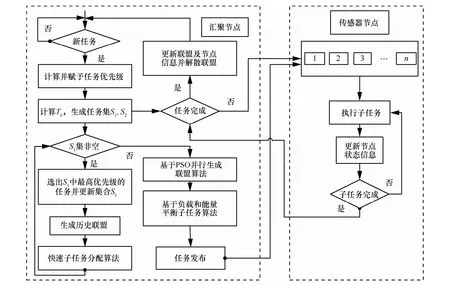
图1 自适应任务分配算法的体系结构

其中，mj为S2下的任务数，K为一常数，Iter_Num为PSO算法的迭代次数，Par_Num为PSO算法中的粒子数，Dmin为集合S2下任务的最早截止期，Dmax则为集合S1中任务的最迟截止期，Cur_Tim为当前时间。

任务可根据截止期的紧迫程度分别被划入集合S1和集合S2，集合S1中任务的截止期紧迫，可根据HCI重新生成历史联盟，并把满足截止期约束作为该集合下唯一的任务分配目标，执行快速子任务分配算法；而集合S2下的任务截止期约束较弱，可采用基于PSO的并行生成联盟算法，在满足任务截止期约束条件下，以节点能耗、负载均衡、网络能量分布平衡为S2集合下任务分配的优化目标，执行基于负载和能量平衡的子任务分配算法。若在当前任务队列还未执行完毕，而新的任务已经到达，则可以回收当前已分配却还未执行的任务，将这些任务和新的任务队列合并为一个任务队列，然后根据上述方案进行任务分配。

4.2 基于PSO的并行生成联盟算法

PSO算法最初被应用于连续空间的优化，然而文中所涉及的并行联盟生成问题本身是一个离散优化问题，需要将基本PSO算法在二进制空间进行扩展，构造一种离散形式的PSO算法模型。本文作者所在的课题组为解决实际工程应用问题，一直跟踪PSO算法的研究进展，很好地将PSO算法用于无线传感器网络任务调度[14]、超大规模集成电路布图规划[19]以及电路划分[20]等问题的应用中，积累了较好的离散PSO算法构造经验。然而文献[14]只涉及到动态联盟的串行联盟机制，并没有考虑并发的多任务分配和任务截止期的约束，本文进一步考虑了任务调度的实时性问题，采用多agent的并行联盟思想，将截止期的概念引入问题求解当中并作为评价联盟性能的指标之一，对不同截止期任务执行不同的子任务分配策略，将无线传感器网络中任务调度的联盟并行生成机制和自适应调整机制结合。借助前期的算法构造经验并对照 PSO算法的基本思想可以发现，可以利用矩阵形式的二进制编码方式表示并行联盟生成问题，以节点能耗、网络能量分布平衡为优化目标定义相应的适应度函数用于指导演化过程已得到优化的结果，从而本文同样选用全局优化能力更强的 PSO算法进行联盟生成问题的求解。

4.2.1 粒子的编码

粒子的编码分别采用一个m×n的矩阵X和V表示[22]，其中，粒子xij(0 ≤i＜m, 0 ≤j＜n)表示如下

则粒子速度与位置的更新公式如下

其中，X(i)和V(i)分别表示第i个粒子的位置和速度，pBest(i) 是第i个粒子的最优值，gBest是全局最优值，w是惯性权值，c1和c2为加速因子，r1和r2是在[0,1]范围内的2个随机数，rand()是[0,1]范围内的随机函数，sigmoid(V)=1/(1+exp(-V))。

w作为更新公式的一个重要参数，合适的w值能够取得全局和局部搜索的平衡，为了提高PSO的全局搜索性能，这里采用经典的线性递减方式[23]

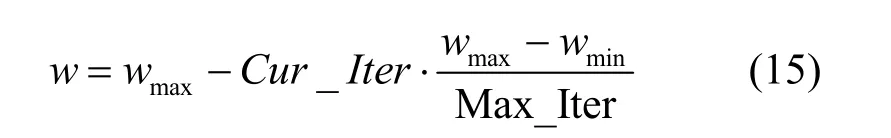
其中，Cur_Iter是当前迭代次数，Max_Iter是最大迭代次数，wmax和wmin分别是初始和最终惯性权值。

4.2.2 适应值函数

由3.2节可知，无线传感器网络任务分配动态联盟模型是一个多目标优化问题，这里采用线性加权和方式转化为单目标优化问题，以期在截止期、网络能耗和网络能量平衡度3个性能指标取得一个折中的任务分配方案。

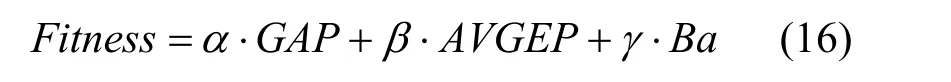
其中，α、β和γ为加权因子。

4.2.3 算法描述

步骤1 随机产生每个粒子的初始位置和初始历史最佳位置pBest，产生全局最佳位置gBest。

步骤2 评价当前各个粒子的适应值，计算每个粒子的评估函数。

步骤3 如果粒子当前位置比历史最佳位置pBest好，更新pBest。

步骤4 如果粒子当前位置比全局最佳位置gBest好，更新gBest。

步骤 5 根据式(13)和式(14)更新粒子的速度和位置。

步骤6 若满足条件，则输出群体的最优值gBest并结束，否则转步骤2。

4.3 子任务分配算法

图2给出了B(i)与ER(i) 2个数据标准化函数曲线，其中，B(i)代表第i个节点的繁忙程度，是通过Sigmoid函数将第i个节点的未来持续繁忙时间Bzyi(0＜i＜n)映射到区间[0, 0.5]，具体计算式如下

其中，Bzymax与Bzymin分别指当前联盟内最繁忙节点的忙碌时间及最空闲节点的忙碌时间。

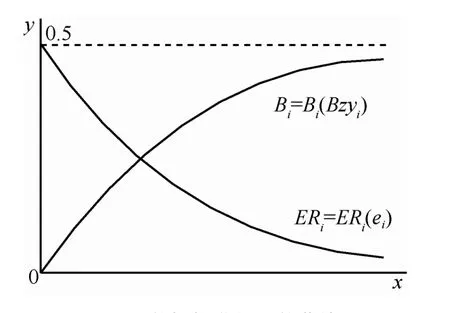
图2 数据标准化函数曲线

同样地，这里节点的剩余能量程度ER(i)也是通过Sigmoid函数将第i个节点的剩余能量值ei(0＜i＜n)映射到区间[0,0.5]，具体计算式如下

其中，emax、emin分别表示当前联盟内节点具有的最大剩余能量值与最小剩余能量值。

综上，节点效能函数U(i)是节点i繁忙程度B(i)和剩余能量程度ER(i)的加权和，其值越小表示节点的综合性能越好。

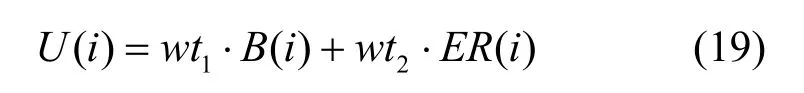
其中，wt1和wt2为权重系数。

针对无线传感器网络任务调度的实时性及节点计算及能量受限的特点，本文根据任务截止期的紧迫程度设计 2个不同的子任务分配算法。对S1集合下截止期紧迫的任务，这里采用快速子任务分配算法，仅把在截止期前完成任务作为子任务分配的唯一目标，算法的具体描述如下。

步骤1 在给定一联盟内，根据式(17)，汇聚节点选择一个具有最小负载值B(i)作为当前待考虑的节点。

步骤 2 该节点挑选其最擅长并未被分配的子任务，被选中的子任务将被映射到该节点待执行。

步骤 3 汇聚节点更新该节点所对应的B(i)、ER(i)和U(i)值。

步骤 4 若存在子任务尚未分配，转步骤 1，否则结束。

针对S2集合下的任务，本文设计了一个基于负载和能量平衡的子任务分配算法，该算法同时考虑联盟内成员节点的剩余能量与当前负载信息，优先挑选剩余能量较多的节点执行子任务，使得联盟内具有较多能量的节点优先承担任务，算法的具体流程如下。

步骤1 根据式(19)，汇聚节点挑选一个具有最小U(i)效能值的联盟成员节点。

步骤 2 针对被选中的节点，挑选其擅长的并未被分配的子任务，被选中的子任务将被映射到该节点待执行。

步骤 3 汇聚节点更新该节点对应的U(i)、B(i)、ER(i)值。

步骤 4 若存在子任务尚未分配，转步骤 1，否则结束。

5 仿真实验与结果分析

贪心算法和随机算法是2种经典的任务分配算法[24,25]，为了说明本文提出算法（简称ERTAA）的有效性，在本文所设计的任务分配体系结构下，融入贪心算法与随机算法分别设计了基于最小完成时间的子任务贪心分配算法(MCTSAA, minimum complete time sub-task allocation algorithm)及随机子任务分配算法(RSAA, random sub-task allocation algorithm)，并将其分别应用于各自算法的子任务分配环节，并通过大量的实验来进行分析与对比。文中主要通过以下3个方面比较ERTAA、MCTSAA及RSAA算法的性能。

1) 截止期错失率(deadline missing ratio)：错失截止期的任务数目与感知到的任务总数的比例。

2) 平均能量消耗(average energy consumption)：无法满足截止期约束的任务不予调度执行，不消耗能量，故为衡量特定算法下能耗指标的优劣，本文所指的平均任务能耗均为被成功执行任务的平均能量消耗。

3) 剩余能量平衡度(remaining energy balance)：表示网络中节点剩余能量的分布平衡度，该值越小表示网络中的节点能量分布的越均衡，计算如式(6)所示。

5.1 实验环境设置

假设节点数n设为100，任务数m为100，同时随机在100 m×100 m的范围内生成各节点坐标，并根据节点坐标位置计算出任意节点之间距离d，任务最多可拆分为不同的子任务数目l被置为12。每个任务的通信节点对数p及需要两子任务通信的子任务编号j1与j2分别由位于(0,l/2]及(0,l]区间的随机整数。每个任务的子任务处理需要reqij均匀分布在区间(2, 6]范围，同等条件下值越大表示需要处理的时间越久，体现了任务处理的难度；节点对不同子任务处理能力bi,j均匀分布在区间(15, 25]，值越大表示节点的处理对应子任务的能力越强；节点处理不同子任务的单位能耗cosi,j均匀分布在区间(3,7]，值越大表示节点单位计算耗能越多。任务截止期di均匀分布在区间(2, 5]，节点初始能量ei均匀分布在区间(45 000, 55 000] mJ。

为了评价和分析本文ERTAA算法的性能，采用主频为2.00 GHz的PC机在VC环境下对ERTAA、MCTSAA和RSAA 3个算法进行一系列的仿真实验，通过多次实验，本文算法的参数按如下设置可以在较短的时间取得优质解：粒子最大速度Vmax为2.5，最大迭代次数Max_Iter为50，粒子个数为30，wmax与wmin为0.9与0.5，c1和c2都为2，α、β和γ分别为0.6、0.3和0.1，wt1和wt2为0.7和0.3。

5.2 实验结果分析

5.2.1 不同任务截止期对性能的影响

下面先通过一组实验来观察任务截止期对无线传感器网络任务分配性能的影响，通过对相同的任务赋予不同的截止期加以测试，设置任务截止期分别在区间(0, 0.5]、[0, 1]、[0, 1.5]、[0, 2]、[0, 2.5]、[0, 3]服从均匀分布，同时采用任务截止期(0, 0.5]的区间环境设置固定的T0值，使得T0值不因实验截止期的变化而变化。

如图3所示，在任务截止期错失率方面，与算法RSAA相比较，ERATA与MCTSAA能够较好地满足任务的截止期约束。当任务截止期位于较为紧迫的(0,0.5]区间时，由于此时的截止期约束过分苛刻导致了3个算法效果都较差，而随着任务截止期限值不断增大，ERATA和MCTSAA的截止期错失率下降的速度分别都超过了RSAA算法，这是因为ERATA与MCTSAA都考虑了传感器节点的负荷，实时动态地根据节点繁忙程度而进行任务分配。而当针对截止期约束宽松的任务时，由于ERATA额外考虑网络节点的能量分布因素，从而效果略微不如MCTSAA，但2个算法的结果非常接近。而对于RSAA，它总是随机地在网络中挑选节点执行任务，这意味着该算法几乎没有考虑在满足任务截止期约束下如何改善网络的性能，因此RSAA在该指标下性能最差。

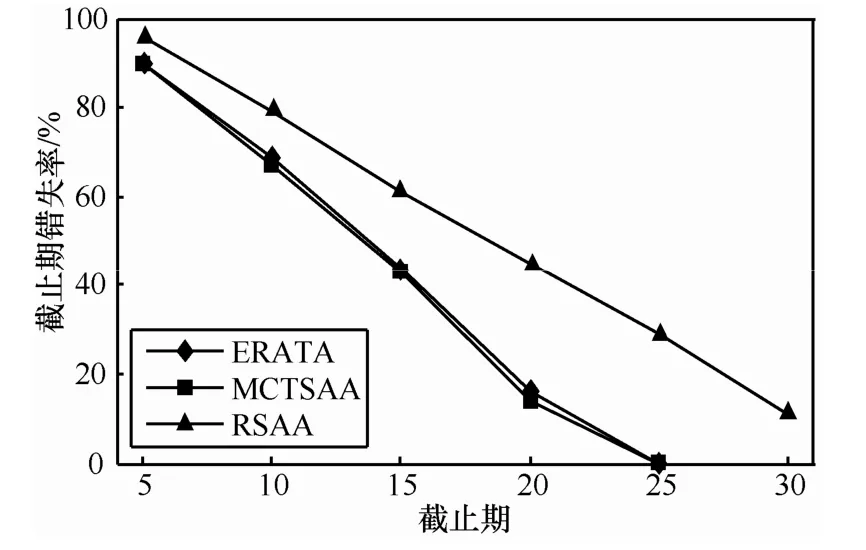
图3 不同截止期下的截止期错失率

图4和图5分别为不同截止期约束下剩余能量平衡度及平均能量消耗的结果比较。由图可知，随着任务截止期值增大，3个算法的剩余能量平衡度及平均能耗都有下降，但 ERATA效果最好，MCTSAA最差，这主要是因为 ERATA不仅考虑了任务截止期约束，而且综合考虑了节点负载和剩余能量因素，而MCTSAA算法则一味地追求最快速完成任务，不对其他性能指标做任何优化。

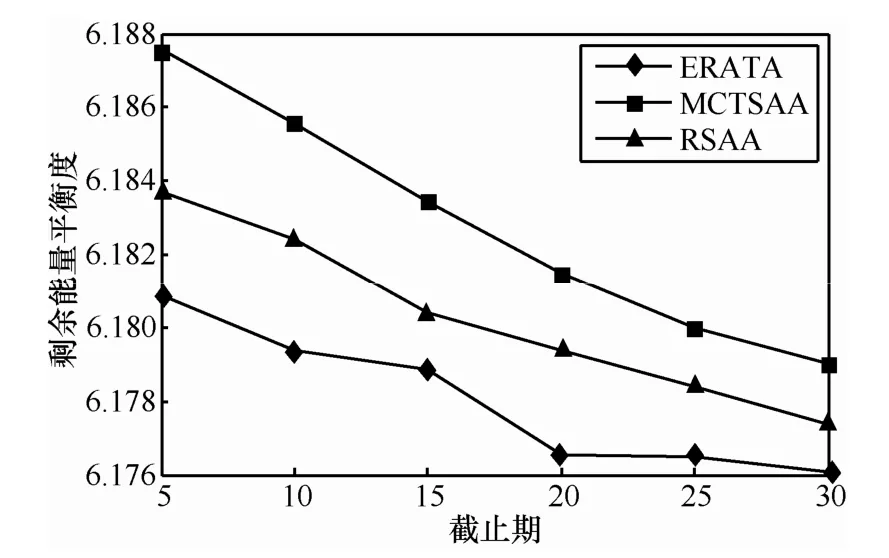
图4 不同截止期下剩余能量平衡度

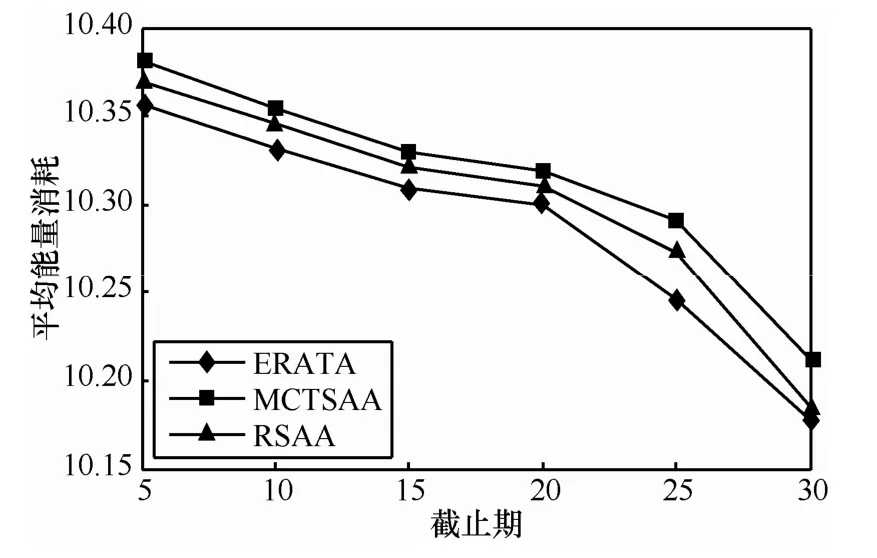
图5 不同截止期下平均能量消耗

由于截止期紧迫会导致采用RSAA的截止期错失率较高，任务分配的成功率较低，多数任务无法得到调度，从而网络整体能耗较少。为了进一步进行实验对比，不失一般性，这里针对任务截止期均匀分布在(0, 2.5]区间的任务对网络的生命周期和网络失效后的平均剩余能量进行测试，同时对所有节点的初始剩余能量重置为1 500 mJ，其他参数未变，结果如表1所示。其中，网络的生命周期用回合数来表示，该值表示某种算法能够运行直至网络失效的次数。

表1 网络的生命周期与平均剩余能量

从表1可以看出，由于ERATA综合考虑了节点当前负载及节点剩余能量的平衡，采用 ERATA算法网络的生命周期明显高于采用 MCTSAA与RSAA算法。另外，由于ERATA对截止期较为宽裕的任务多数采用了基于负载和能量平衡的子任务分配算法，很好地均衡网络能量并延长网络的生命周期，从而当网络失效时，ERATA节点的平均剩余能量会显著低于另外2个算法。

5.2.2 不同节点数对性能的影响

本节通过一组实验来观察网络中不同节点数目对任务分配的影响，不失一般性，对截止期随机分布在(2, 5]区间的任务，分别对具有40、60、80、100、120、140个节点的网络进行了测试，各个节点的剩余能量均匀分布在[45 000, 55 000]mJ范围，具体结果如图6和图7所示。

从图6中可以看出，初始由于可用节点数目较少，任务数量过多，无法确保任务在截止期前完成，但随着节点数目增加，3种算法截止期错失率都呈现迅速下降的趋势，ERATA和MCTSAA下降尤其明显，且曲线基本重合，这主要是它们都考虑了节点的繁忙程度以及节点处理能力，从而 ERATA和MCTSAA在截止期错失率方面明显优于RSAA，能够较好地满足任务截止期要求。从图7可知，随着节点数目不断增加，任务的平均能量消耗也都呈下降趋势，这主要是因为可供选择节点变多，可提供更具节能的选择，同上节实验，可知ERATA具有较少的能量消耗，而MCTSAA为尽早完成任务，以能耗为代价，未考虑节能优化，导致消耗最多的能量。

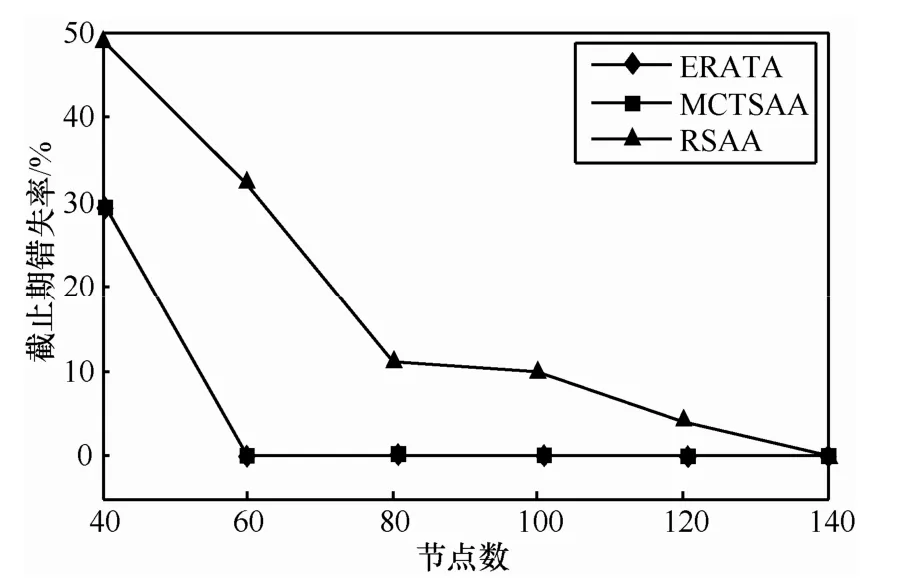
图6 不同节点数下的截止期错失率

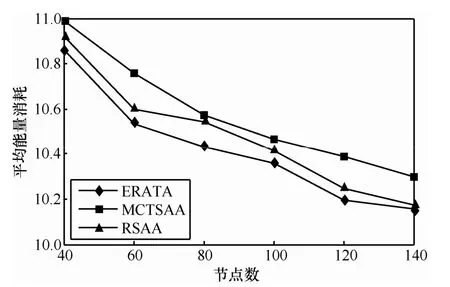
图7 不同节点数下任务的平均能量消耗

表2列出3种算法不同节点数情况下剩余能量平衡度的对比结果，由表2可知，随着节点数的增加，3种算法剩余能量平衡度都随之增大，在同等情况下，ERATA的效果略优于MCTSAA与RSAA，这主要是因为面对不紧迫的任务，ERATA采用了基于负载和能量平衡的子任务分配算法，该算法将节点剩余能量纳入考虑范围，有利于具有较多能量的节点优先选择子任务执行，进而均衡网络节点能量分布，从而在网络具有相同总能量情况下，ERATA更能延长网络生命周期。

表2 不同节点数下的剩余能量平衡度

5.2.3 不同任务数对性能的影响

为测试不同任务数目对任务分配性能的影响，本节针对能量均匀分布在[45 000, 55 000] mJ区间的100个传感器节点，对具有50、100、150、200、250、300个不同的任务进行模拟仿真，不失一般性，设置任务截止期均匀分布在[2, 5]的区间范围。

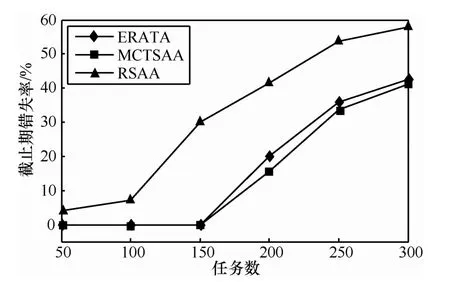
图8 不同任务数下的截止期错失率

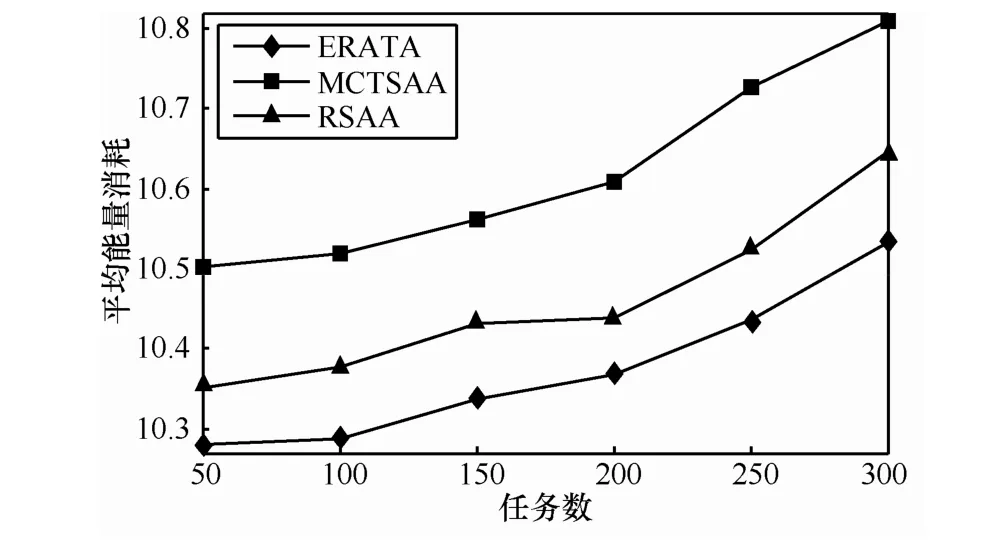
图9 不同任务数下任务的平均能量消耗

表3列出3种算法在不同任务数情况下剩余能量平衡度的对比结果，与表2类似，随着任务数的增加，3种算法剩余能量平衡度都随之增大，同等情况下 ERATA算法的效果略优于 MCTSAA与RSAA 2个算法。

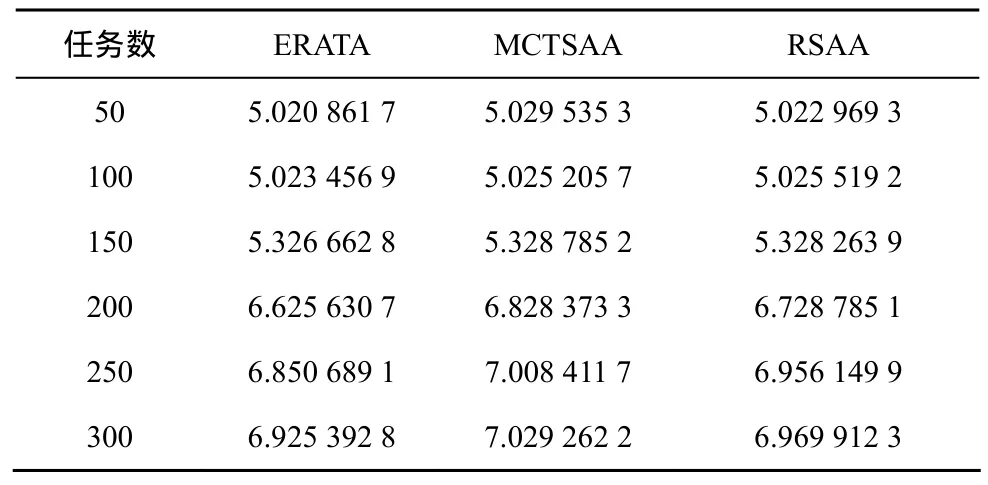
表3 不同任务数下的剩余能量平衡度

6 结束语

无线传感器网络本身所具有的特性要求从实时性、经济性、节能性和动态协调性等方面，改善和满足无线传感器网络对任务调度系统的性能要求。围绕这一中心问题，本文基于动态联盟机制设计了一个无线传感器网络自适应任务分配算法，对截止期较为紧迫的任务采用历史信息生成历史联盟，并执行快速子任务分配算法，而对截止期较为宽裕的任务，构建了一个离散粒子群优化算法以并行生成联盟，并执行基于负载和能量平衡的子任务分配算法。仿真实验结果表明所构造的自适应算法能够较好地满足任务截止期约束，节约节点能耗，均衡网络负载，并在局部求解与全局探索之间能够取得了较好的平衡，在较短的时间内取得满意的解。下一步研究工作重点将进一步考虑容错机制，构建一个具有容错机制的无线传感器网络任务自适应分配算法。

[1] AKYILDIZ I F, SU W, SANKARASUBRAMANIAM Y,et al.Wireless sensor networks: a survey[J]. Computer Networks, 2002,38(4): 393-422.

[2] 朱敬华, 高宏. 无线传感器网络中能源高效的任务分配算法[J]. 软件学报, 2007, 18(5):1198-1207.ZHU J H, GAO H. An energy efficient algorithm for task allocation in wireless sensor networks[J]. Journal of Sofware, 2007, 18(5):1198-1207.

[3] YU Y, VIKTOR K P. Energy-balanced task allocation for collaborative processing in wireless sensor networks[J]. Mobile Networks and Applications, 2005, 10(12): 115-131.

[4] TIAN Y, BOANGOAT J, EKICI E,et al. Real-time task mapping and scheduling for collaborative in-network processing in DVS-enabled wireless sensor networks[A]. Proc of the 20th International Parallel and Distributed Processing Symposium[C]. Island, Greece, 2006.

[5] TIAN Y, GU Y Y, EKICI E,et al. Dynamic critical-path task mapping and scheduling for collaborative in network processing in multi-hop wireless sensor networks[A]. Proc of the 2006 International Conference on Parallel Processing Workshops[C]. Columbus, Ohio,USA, 2006. 215-222.2006. 215-222.

[6] 李志刚, 周兴社, 李士宁等. 传感器网络能源有效任务分配算法[J].计算机研究与发展, 2009, 46(12): 1994-2002.LI Z G, ZHOU X S, LI S N,et al. An energy efficient task assignment algorithm of wireless sensor network[J]. Journal of Computer Research and Development, 2009, 46(12): 1994- 2002.

[7] 易军, 石为人, 唐云建等. 无线传感器/执行器网络任务动态调度策略[J]. 电子学报, 2010, 38(6): 1239-1244.YI J, SHI W R, TANG Y J,et al. A dynamic task scheduling for wireless sensor and actuator networks[J]. Acta Electronica Sinica,2010, 38(6): 1239-1244.

[8] ZENG Z W , LIU A F, LI D,et al. A highly efficient DAG task scheduling algorithm for wireless sensor networks[A]. Proc of the 9th International Conference for Young Computer Scientists[C]. 2008.570-575.

[9] 代亮, 沈中, 常义林等. 无线传感器网络任务调度双层规划方法[J].兵工学报, 2010, 31(12): 1697-1701.DAI L, SHEN Z, CHANG Y L,et al. Bilevel programming method for task scheduling in wireless sensor networks[J]. Acta Armamentarii,2010, 31(12): 1697-1701.

[10] 刘梅, 李海昊, 沈毅. 无线传感器网络空中目标跟踪任务分配技术的研究[J]. 宇航学报, 2007, 28(4): 960-965.LIU M, LI H H, SHEN Y. Research on task allocation technique for aerial target tracking based on wireless sensor network[J]. Journal of Astronautics, 2007, 28(4): 960-965.

[11] 陈剑霞, 于海斌. 一种面向无线传感器网络协同任务分配的动态联盟更新机制[J]. 传感技术学报, 2009, 22(4): 499-504.CHEN J X, YU H B. An updating scheme of the working dynamic coalition for collaborative task allocation in wireless sensor networks[J]. Chinese Journal of Sensors and Actuators, 2009, 22(4):499-504.

[12] ABDELHAK S, GURRAM C S, GHOSH S,et al. Energy balancing task allocation on wireless sensor networks for extending the lifetime[A]. Proc of the 2010 IEEE International 53rd Midwest Symposium on Circuits and Systems[C]. Seattle, Washington, 2010.

[13] 陈国龙, .郭文忠, 陈羽中. 无线传感器网络任务分配动态联盟模型与算法研究[J]. 通信学报, 2009,30(11): 48-55.CHEN G L, GUO W Z, CHEN Y Z. Research on dynamic alliance of task allocation and its algorithm in wireless sensor network[J]. Journal on Communications, 2009,30(11): 48-55.

[14] GUO W Z, XIONG N X, CHAO H C,et al. Design and analysis of self-adapted task scheduling strategies in wireless sensor networks[J].Sensors, 2011, 11(7): 6533-6554.

[15] HEINZELMAN W B, CHANDRAKASN A P, BALAKRISHNAN H.An application specific protocol architecture for wireless micro-sensor networks[J]. IEEE Transactions on Wireless Communications, 2002,1(4): 660-670.

[16] 张国富, 蒋建国, 夏娜等. 基于离散粒子群算法求解复杂联盟生成问题[J]. 电子学报, 2007, 35(2):323-327.ZHANG G F, JIANG J G, XIA N,et al. Solutions of complicated coalition generation based on discrete particle swarm optimization[J].Acta Electronica Sinica, 2007, 35(2): 323-327.

[17] CHETTO H, CHETTO M. Some results of the earliest deadline scheduling algorithm[J]. IEEE Transaction on Software Engineering,1989, 15(10): 1261-1269.

[18] ZHU Z X, ZHOU J R, ZHEN J,et al. DNA sequence compression using adaptive particle swarm optimization-based memetic algorithm[J]. IEEE Transaction on Evolutionary Computation, 2011,15(5): 643-658

[19] CHEN G L, GUO W Z, CHEN Y Z. A PSO-based intelligent decision algorithm for VLSI floor planning[J]. Soft Computing, 2010, 14(12):1329-1337.

[20] 郭文忠, 陈国龙等. 求解 VLSI电路划分问题的混合粒子群优化算法[J]. 软件学报, 2011, 22(5): 833-842.GUO W Z, CHEN G L,et al. Hybrid particle swarm optimization algorithm for VLSI circuit partitioning[J]. Journal of Software, 2011,22(5): 833-842.

[21] KULKARNI R V, VENAYAGAMOORTHY G K. Particle swarm optimization in wireless sensor networks: a brief survey[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part C: Applications and Reviews, 2011, 41(2): 262-267.

[22] GUO W Z, GAO H L, CHEN G L,et al. Particle swarm optimization for the degree constrained MST problem in WSN topology control[A].Proc of the 2009 International Conference on Machine Learning and Cybernetics[C]. 2009. 1793-1798.

[23] SHI Y, EBERHART R C. A modified particle swarm optimizer[A].Proc of the 1998 IEEE International Conference on Evolutionary Computation[C]. Anchorage, Alaska, 1998. 69-73.

[24] LESSER V, ORTIZ C L, TAMBE M. Distributed Sensor Networks: a Multiagent Perspective[M]. Kluwer Academic Publishers, 2003.

[25] ARMSTRONG R, HENSGEN D, KIDD T. The relative performance of various mapping algorithms is independent of sizable variances in run time predictions[A]. Proc of the 7th IEEE Heterogeneous Computing Workshop[C]. Orlando, USA, 1998. 79-87.