应用中值定理验证中值等式的实例分析

汲守峰

（唐山学院 基础教学部，河北 唐山063000）

应用中值定理验证中值等式是高等数学中的重点内容，同时也是教学难点。内容主要涉及连续函数的介值定理（零点定理）和微分中值定理，包括费马定理、罗尔定理（广义罗尔中值定理）、拉格朗日定理、柯西定理［1］、泰勒定理及积分中值定理。另外，利用函数的单调性也可以讨论与中值有关的问题。一般来说，讨论中值的存在性需要用到介值定理、微分中值定理和积分中值定理；讨论唯一性通常利用函数的单调性或反证法，微分中值定理和积分中值定理有时还可以用来求函数极限。以下将通过几个典型的例题进行分析。

1 利用广义罗尔中值定理证明中值等式

例1 设函数f（x）在（0，＋∞）上连续且可微，f（0）＝1，f（x）≤e－x，求证存在一点x0，使得f（x0）＝－e－x0。

证明 首先证明广义罗尔中值定理。

设f（x）在区间［a，＋ ∞）（或（－ ∞，a］）上连续，在（a，＋∞）（或（－∞，a））内可导，且f（x）＝f（a）（或f（x）＝f（a）），则至少存在一点ξ∈ （a，＋∞）（或ξ∈ （－∞，a）），使得f′（ξ）＝0）［1］。

仅在区间［a，＋∞）给出证明。

若f（x）＝f（a），x≥a时结论显然成立。

设x0＞a，f（x0）≠f（a）（不妨设f（x0）＞f（a）时），由连续函数介值定理及f（x）存在且等于f（a）可知，存在x1（x1∈ （a，x0））与x2（x2＞x0），使得

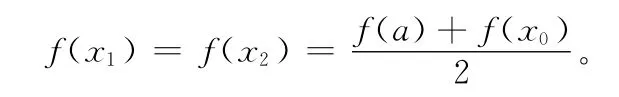
函数f（x）当x＞a时可导，对f（x）在［x1，x2］上应用罗尔中值定理可知，存在ξ∈ ［x1，x2］（a，＋∞），使得f′（ξ）＝0。

本例中，设g（x）＝f（x）－e－x，由f（x）连续且可导知g（x）也连续可导，且g（0）＝f（0）－e－0＝0g（x）＝0，由广义罗尔中值定理知，存在x0∈（a，＋∞），使得g′（x0）＝f′（x0）＋＝0，即f（x0）＝－.

2 利用微分中值定理证明中值等式

例2 设函数f（x）在［－2，2］上二阶可导，且｜f（x）｜≤1，f′（0）＋［f′（0）］2＝4，证明在（－2，2）内至少存在一点x0，使得f（x0）＋f″（x0）＝0。

证明 由拉格朗日中值定理可知，存在x1∈（－2，0），x2∈ （0，2），使得

f（0）－f（－2）＝2f′（x1），f（2）－f（0）＝2f′（x2）。

因为｜f（x）｜≤1，所以

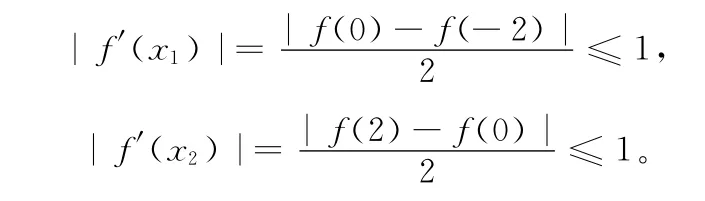
令 g（x）＝ f2（x）＋ ［f′（x）］2，则 ｜g（x1）｜≤ 2，｜g（x2）｜≤2，因为g（x）在［x1，x2］上连续，且g（0）＝4，若设g（x）在［x1，x2］上的最大值g（x）≥4，显然，g（x）取最大值的点在（x1，x2）内，即g（x0）＝g（x），又g（x）在［x1，x2］上可导，由费马定理可得g′（x0）＝0，即

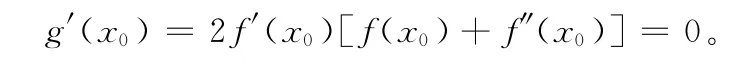
由于g（x）≥4，可知f′（x0）≠0（若不然，f′（x0）＝0，则有g（x0）＝f2（x0）≥4｜f（x0）｜≥2，与｜f（x）｜≤1矛盾），于是f（x0）＋f″（x0）＝0，x0∈ （－2，2）。

例3 设函数f（x），g（x）在［a，b］内存在二阶导数，且g″（x）≠0，f（a）＝f（b）＝g（a）＝g（b）＝0。则以下结论成立：（1）g（x）≠0，x∈ （a，b）；（2）存在ξ∈ （a，b），使得

证明 （1）若存在c∈（a，b），g（c）＝0，由罗尔中值定理可 知，存在c1∈ （a，c），c2∈ （c，b），使得g′（c1）＝g′（c2）＝0，再由g（x）在［a，b］上存在二阶导数，对g′（x）由罗尔中值定理可知，存在η∈（c1，c2），使g″（η）＝0，这与g″（x）≠0矛盾，故特设成立。

（2）令h（x）＝f（x）g′（x）－f′（x）g（x），由f（x），g（x）在［a，b］内存在二阶导数，所以h（x）在［a，b］上可导。又f（a）＝f（b）＝g（a）＝g（b）＝0，则h（a）＝h（b）＝0。

由罗尔中值定理可知，存在ξ∈ （a，b），使得h′（ξ）＝f″（ξ）g（ξ）－g″（ξ）f（ξ）＝0，由（1）及g″（x）≠0，得

例2和例3的证明除了对微分中值定理能够熟练运用外，根据题意构造函数也是非常关键的一个环节，构造的函数既要符合在区间上连续与可导的性质，还要求其一阶导数能与结论中的函数相吻合。一般来讲，可直接根据结论构造函数，也有部分题目中并未明确构造的函数类型，构造辅助函数时需要一定的技巧，但也有规律可循。

3 利用积分中值定理证明中值等式

例4 设函数f（x）在［0，1］上连续，在（0，1）内可导，f（1）＝f（x）dx（c＞1），证明至少存在一点ξ∈ （0，1），使得f′（ξ）＝ （1－ξ－1）f（ξ）。

因为e1－ξ0，所以f′（ξ）＝ （1－ξ－1）f（ξ）。

利用积分中值定理去验证中值等式时，也可以用积分中值定理的推广形式［3］：

函数f（x）在（a，b）上连续，而在x＝a及x＝b为第一类间断点，或只有一个第一类间断点而另一间断点是连续点，则在（a，b）上至少存在一点ξ，使f（x）dx＝f（ξ）（b－a）。

4 利用单调性或反证法讨论中值的唯一性

例5 设f（x）在（a，b）内可导，证明f（x）的任何两个不同的零点之间一定有函数f（x）＋f′（x）的一个零点，并由此证明方程（x－2）ln（x－1）＋＝0在（1，3）内有且仅有一个实根。

证明 假设f（x）在（a，b）上任意两个不同的零点为x1，x2（x1＜x2），即f（x1）＝f（x2）＝0，由f（x）＋f′（x）＝0，解该微分方程得f（x）＝Ce－x（C为任意常数），构造函数令g（x）＝exf（x），则函数g（x）在［x1，x2］上连续，在（x1，x2）上可导，且g（x1）＝g（x2）＝0，由罗尔定理可知，至少存在一点ξ∈ （x1，x2），使得g′（ξ）＝0，即ex（f（ξ）＋f′（ξ））＝0，也就是f（ξ）＋f′（ξ）＝0。

构造函数f（x）＝ （x－3）ln（x－1），则f′（x）＝ln（x－1）＋，f（1）＝f（3）＝0，且f（x）在（1，3）内可导，x＝11，x2＝3是f（x）的两个零点，由前面所证结论可知，在（1，3）内一定存在f（x）＋f′（x）＝ （x－2）ln（x－1）＋的一个零点，即方程（x－2）ln（x－1）＋＝0在（1，3）内至少有一个实根。

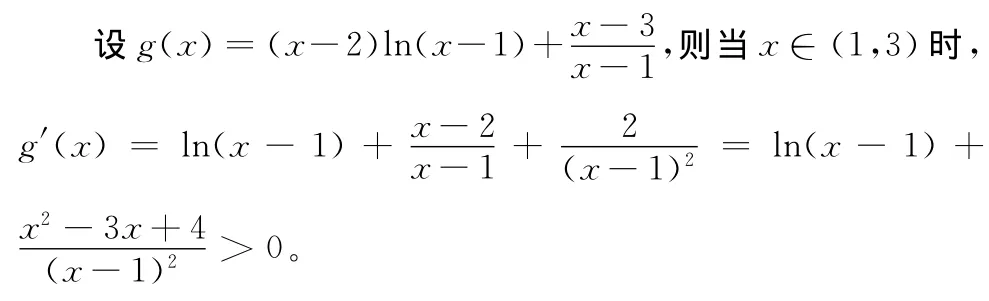
所以g（x）在（1，3）内严格单调递增，因此方程g（x）＝0在（1，3）内至多有一个实根，方程（x－2）ln（x－1）＋＝0在（1，3）内至多有一个实根。

5 结语

介值定理、中值定理不仅可以用来验证中值等式，而且还可以证明一些不等式方程。验证中值的唯一性时除了单调性外还可以用反证法等方法。

［1］ 同济大学数学系.高等数学：上册［M］.6版.北京：高等教育出版社，2007：136.

［2］ 刘玉琏.数学分析讲义［M］.北京：高等教育出版社，2004：212－213.

［3］ 王海玲.微分中值定理的推广及应用［J］.长春理工大学学报，2003（3）：81－85.