经济数学中微分方程案例教学的探索

庄科俊 杨鹏辉

(安徽财经大学统计与应用数学学院，安徽蚌埠 233030)

经济数学是各高校财经类专业设置的核心课程之一，是高等学校经管类各专业的一门重要基础课，在培养高素质科学技术人才中具有独特的、不可替代的重要作用。经济数学有着完整的系统性和逻辑性，概念的形成源于实践，又高于实践，教学中应贯彻“数学为本，经济为用”的思想。然而，传统的经济数学教学往往与专业需求相脱节，将重点放在数学公式的推导及计算方面，而忽略了该课程在经济方面的应用性。目前，已有文献就如何将数学建模的思想融入经济数学课程作了初步探索［1］。因此，本文将以微积分中的常微分方程这部分内容为例，尝试将数学建模思想融入课堂教学，探讨微分方程在经济分析中的应用实例，以加强数学和后续课程的联系，并进一步提高学生的数学素养。

在经济管理和科学技术问题中，往往需要寻找与问题有关的变量之间的函数关系，且需对函数关系予以研究。针对实际经济问题，经过分析、处理和适当简化后，列出的含有未知函数及其导数的关系式，就是常微分方程［2］。在现行的微积分教材中，通常会介绍各种一阶微分方程、二阶常系数线性微分方程的求解，这就让学生产生一种错觉，这部分内容就是计算，没有实际用处。其实不然，下面将分别给出一些具有经济学背景的案例［2-5］。

1 一阶微分方程模型举例

例1(国名经济总值翻番问题)若国民经济总值每年的递增率为7% ，试问:多少年后方可使国民经济总值翻两番?

解:(1)建立数学模型

设国民经济总值为N，且N随时间t的变化而变化。所谓国民经济增长率7%就是国民经济总值N对时间t的变化率，也就是导数dN/dt。于是，所求问题可归结为下列微分方程的初值问题:

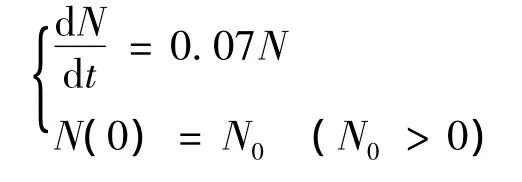
(2)求解数学模型

这是一个可分离变量的微分方程，通过分离变量、两边积分、代入初始条件，可解得特解N(t)=N0e0.07t，即为国民经济总值N与时间t的函数关系。

(3)作出分析

要使国民经济总值翻两番，即4N0=ln4=0.07t，解得t≈20，这就是说，按7% 的增长率，国民经济总值用20a的时间就可翻两番。

例2(新产品的推销问题)设有某种耐用商品在某地区进行推销，最初商家会采取各种宣传活动以打开销路。假设该商品确实受欢迎，则消费者会相互宣传，使购买人数逐渐增加，销售速率逐渐增大，但由于该地区潜在消费总量有限，所以当购买者占到潜在消费总量的一定比例时，销售速率又会逐渐下降，且该比例越接近于1，销售速率越低，这时商家就应更新商品了。假设消费者总量为N，任一时刻t已出售的新商品总量为x(t)，试建立x(t)所应满足的微分方程;并分析x(t)的性态，给出商品的宣传和生产策略。

解:(1)建立数学模型

设在该地区t时刻已售出的该新商品的总量为x(t)，由于潜在消费者总量为N，则在销售初期或当N很大时，该商品销售速率主要受已购者数量x(t)的影响，即每一个已购者在一定时间内吸引若干个欲购者，所以销售速率近似值与已购者的数量x(t)成比例。

但在销售后期或N很小时，该商品的销售速率将主要受未购者数量(N-x(t))的影响，即销售速率近似值与未购者的数量(N-x(t))成比例。综合考虑上述因素，可以认为产品销售速率和x(t)与(N-x(t))的乘积成比例，得到如下模型:

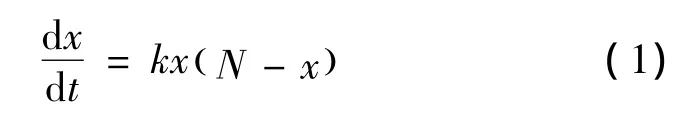
其中k是比例常数，这一模型正是经典的Logistic模型。在许多情况下，统计资料证实它与实际情况相符得很好。

(2)求解模型

(3)分析结果

取k=0.1，N=100，x0=1时，可画出Logistic模型的曲线(见图1)，呈S型曲线，从图形上可以看出，曲线存在拐点，通过计算知拐点为 (t0，50)。这说明，在销出量小于最大需求量的一半时，销售速率不断增大，而当售出量大于最大需求量的一半时，销售速率不断减少，销售量在最大需求量的一半左右时，商品最为畅销。

图1 方程(1)的解曲线

通过对 Logistic模型的分析认为，从20%到80%的用户采用某种新产品的这段时期，应为该产品正式大批量生产的时期，初期应以较小批量生产并加强宣传，而到后期则应适时转产。

2 考虑库存影响的价格调整模型

一般的微积分教材中，很少有涉及到直接的二阶微分方程模型，为了弥补这一不足，这里给出基于二阶常系数非齐次线性微分方程的价格调整模型。

商品的供给函数和需求函数是经济学研究的一个基本任务，在简化的条件下，可以认为需求函数与供给函数都是关于价格P(t)的线性函数，可分别表示为QD(t)=a-bP(t)与QS(t)=c+dP(t)，其中a，b，d均为正常数。在商品市场未达到均衡时，价格的变化率和需求函数与供给函数的差值成正比，即

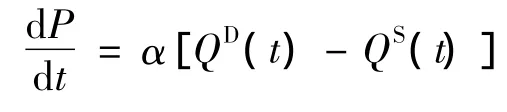
这就是著名的瓦尔拉斯价格调整模型，正数α称为价格调整强度系数。可以想象，当商品供大于求，而剩余供给又不销毁时，就会出现库存。到时间t为止的商品库存量K(t)可表示为QD(s)］ds，可以合理地认为库存量的存在会促使价格下降，因此，可将前述价格调整模型修正为

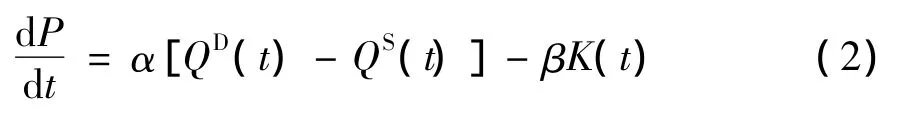
其中β是库存导致的价格调整强度系数，将式(2)对时间再求导一次，并由，可以得到下列的考虑库存影响的价格调整模型:

这是一个二阶常系数非齐次线性微分方程，价格P(t)的均衡解(即数学上的平衡点，也是一个特解)为P*=(a-c)/(b+d)。根据解的结构原理，只需求出对应齐次方程的特征根，即可写出非齐次方程(3)的通解。

对参数取不同值，可以得到不同的解的形式，并借助Matlab画出解曲线，以加深学生对微分方程解的印象。特别地，当 a=700，b=20，c=-80，d=30，β=0.03时，均衡价格P*=15.6，取α为0.01与0.05时的解曲线分别见图2、3。经过一段时间后，商品价格会趋于均衡价格，达到动态的平衡，并且，系数α变大时，趋于均衡价格的速度也越大。

3 混沌金融系统

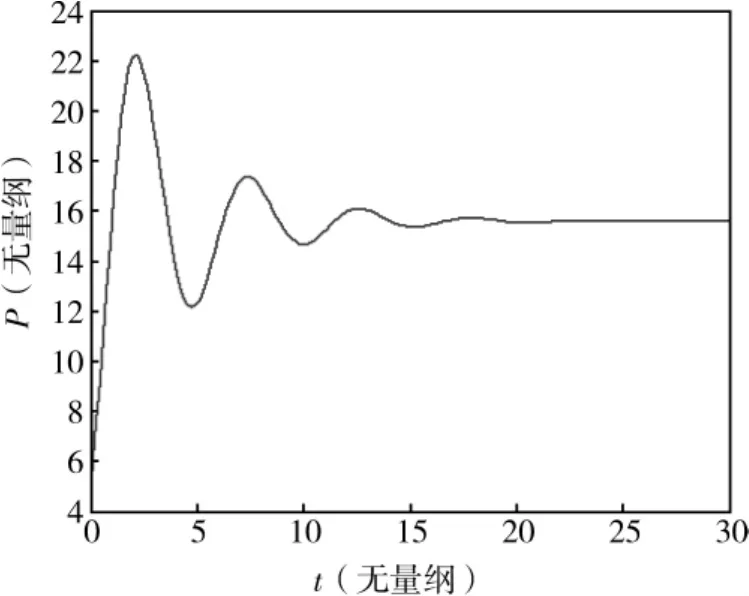
图2 α=0.01时方程组(3)的解曲线

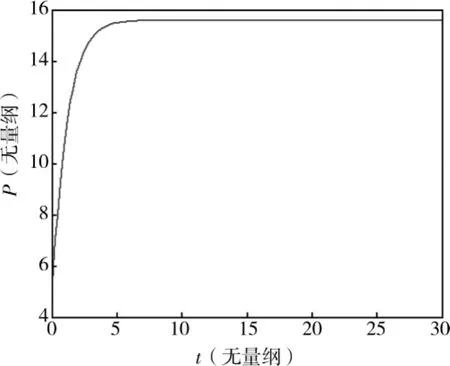
图3 α=0.05时方程组(3)的解曲线

在讲授传统的微积分内容时，也可适当介绍一些较新的研究成果。微积分教材通常给学生造成一种误觉，所有的常微分方程都是可解的。但事实并非如此，应该说，绝大部分常微分方程是无法求出解析解的，只能求得其数值解。

例如，文献［5］建立了一个由生产子块、货币、证券子块和劳动力子块所组成的混沌金融系统，可以用下列三维的常微分方程组表示:

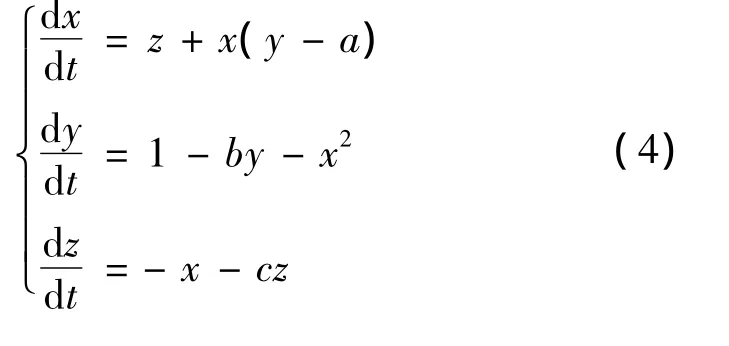
式中:x— 利率;y— 投资需求;z— 价格指数;a≥0为储蓄量;b≥0为单位投资成本;c≥0为商品需求弹性。

方程组(4)看似简单，却无法求出解析解，并且具有非常复杂的动力学性质。当a=3，b=0.1，c=1，初值为(2，3，2)时，利用 Matlab可以画出解的空间相图(图4)，此时有混沌吸引子，俗称“蝶形图”。对模型(4)，无需介绍太多的理论知识，只需说明该系统的经济学含义即可，让学生欣赏混沌吸引子的空间相图。即使是简单的常微分方程组，也可能出现复杂的混沌现象，从而激发学生学习微积分的兴趣，拓宽知识面。

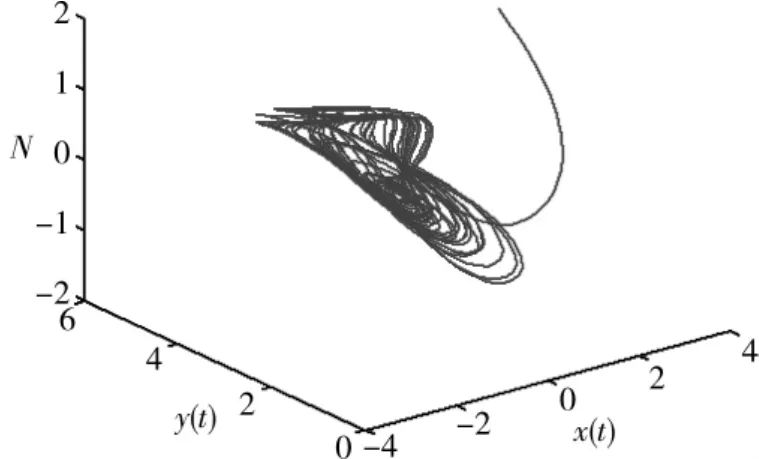
图4 方程组(4)的空间相图

［1］钱和平，徐清舟.数学建模融入经济数学教学中的案例及分析［J］. 大学数学，2012，28(3):92-96.

［2］吴传生.经济数学 —— 微积分［M］.北京:高等教育出版社，2008.

［3］何良材，何牧.数学在经济管理中应用实例析解［M］.重庆:重庆大学出版社，2007.

［4］王兴德.动态经济学图解［M］.上海:上海财经大学出版社，2012.

［5］黄登仕，李后强.非线性经济学的理论和方法［M］.成都:四川大学出版社，1993.