基于不安全度模型的煤矿安全监测系统设计

吕刚 陈圣兵

(合肥学院网络与智能信息处理重点实验室，合肥 230601)

煤矿安全生产是各国煤炭行业的共同话题，各国政府都很重视。我国煤矿井下生产条件复杂，地质条件多变，自然灾害较为严重［1］。我国煤矿安全状况和生产水平与世界发达国家相比，仍有相当大的差距。本文通过对影响煤矿安全生产因素的分析，通过建立模型与计算机仿真对一种小型煤矿安全监测系统进行设计与实现。

1 监测数学模型设计

1.1 不安全度

本文将煤矿安全监测问题归结于讨论判断该煤矿不安全的程度(即发生爆炸事故的可能性)有多大。将造成煤矿安全的因素，即瓦斯浓度、煤尘浓度及它们与温度、含氧量之间的相互关系，均转换为一个度，称为不安全度。通过判断不安全度所在的范围来决定危险程度，从而及时采取相应措施消除危险。这样将很多复杂的变量及关系化简为一个不安全度来分析，使得问题更简单明了，也便于计算机仿真的实现。

1.2 模型的建立

1.2.1 瓦斯的绝对涌出量

根据单位时间的通风量等于巷道的横截面积与通风速度［2］的乘积，可以得到第k个监测点的通风量为:Qk=Skvk，Sk巷道横截面积(m2)、vk巷道风速(m/s)。根据瓦斯绝对涌出量等于风量乘以瓦斯浓度，可以得到第k个监测点的瓦斯绝对涌出量Ak，Ak=Qkcgk，cgk为瓦斯的平均浓度(%)。

1.2.2 瓦斯浓度与风速的关系

各个工作面和回风巷的瓦斯浓度除了与风速有关以外，还与瓦斯的涌出量有关，而且涌出量是一个不可控的因素，即瓦斯的涌出量是不确定的。实际上，瓦斯的浓度与风速成反比，与巷道截面面积成反比。于是各监测点的瓦斯浓度与风速的近似关系为:

其中εk是随机误差，不妨设 εk服从于正态分布N(0，σk)。根据大量的监测数据作最小二乘拟合系数ak和方差σk如表1所示。

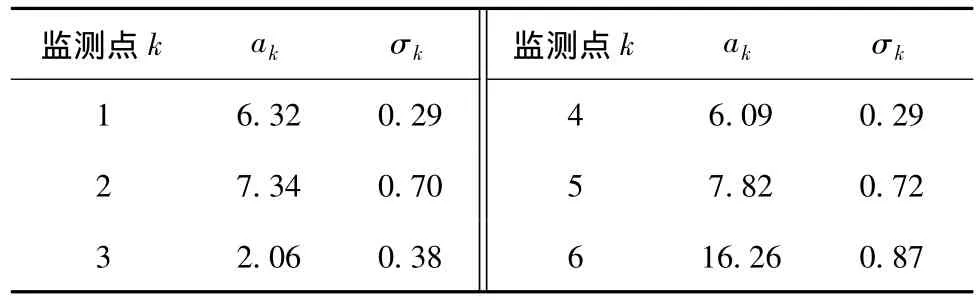
表1 瓦斯浓度与风速的关系拟合系数

由此即可得到各工作面与回风巷的瓦斯浓度随风速变化的近似关系。

1.2.3 煤尘浓度与风速的关系

矿井中煤尘浓度只与风速有直接的关系。一般来说，煤尘与风速应该呈非线性的关系，但实际监测出的风速变化范围很小，相对比较稳定，而且都在1.9 m/s以上。为此，在较小的范围内可近似为线性关系，于是不妨假设各监测点的煤尘浓度与风速的关系近似为:

根据大量的监测数据作最小二乘拟合可得拟合系数见表2。

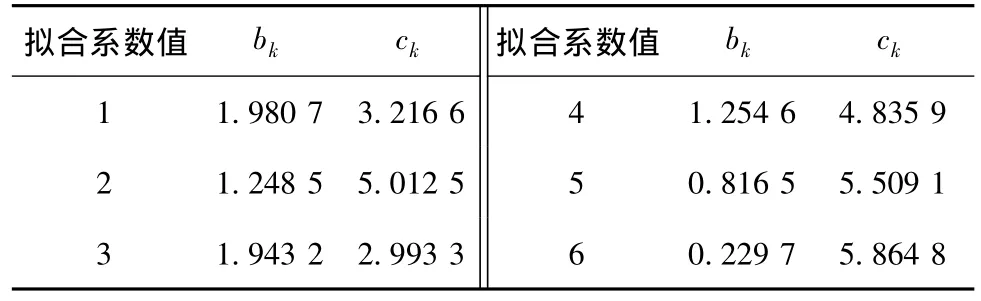
表2 煤尘浓度与风速的关系拟合系数

由此即可得到各工作面与回风巷的煤尘浓度随风速变化的近似关系。

1.2.4 空气中的瓦斯浓度与煤尘爆炸下限的关系

瓦斯参与使煤尘爆炸下限降低。瓦斯浓度低于4%时，煤尘的爆炸下限可用下式计算:

式中:δm—空气中有瓦斯时的煤尘爆炸下限，g/m3;δ—爆尘的爆炸下限，一般为30～50 g/m3;k— 降低系数。

瓦斯浓度对煤尘爆炸下限的影响系数见表3。

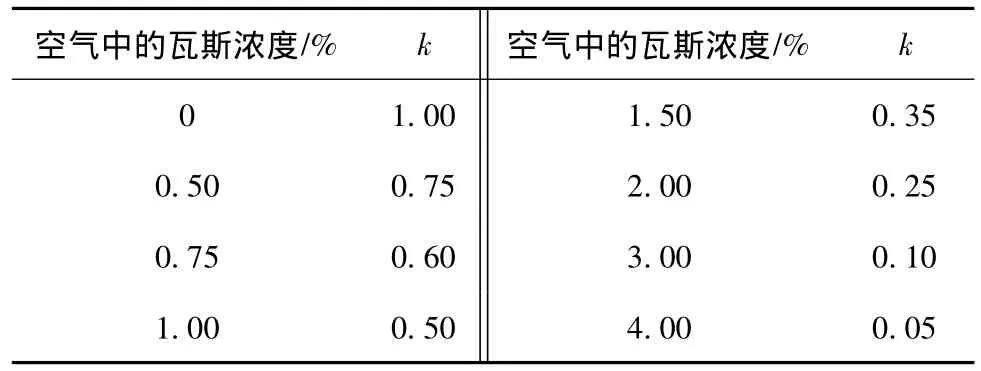
表3 瓦斯浓度对煤尘爆炸下限的影响系数

1.2.5 瓦斯与煤尘影响的不安全度模型

将不安全程度分为由瓦斯浓度引起的不安全程度和由煤尘浓度引起的不安全程度2个部分，取其中最大值作为矿井的不安全度，即

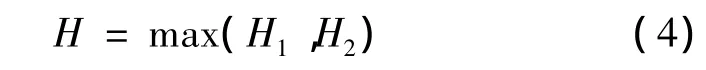
(1)由煤尘浓度引起的不安全程度

煤尘浓度的影响是由于浓度与爆炸下限的临近，引起了矿井的不安全事故，根据式(3)选取爆炸下限组中的值进行拟合，得到煤尘的爆炸下限与瓦斯浓度的关系式为:

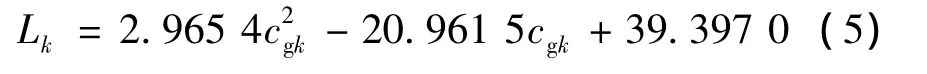
构造倒数模型为:

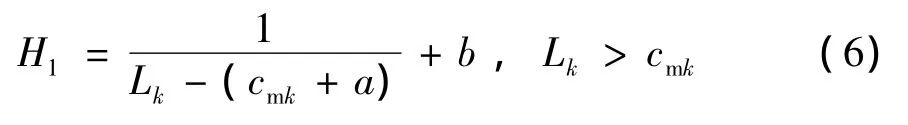
当煤尘的浓度为0时，不安全程度为0;当煤尘的浓度为Lk时，不安全程度为1［4］，即100%。带入模型，可得:

结合实际，求解方程组，可得:

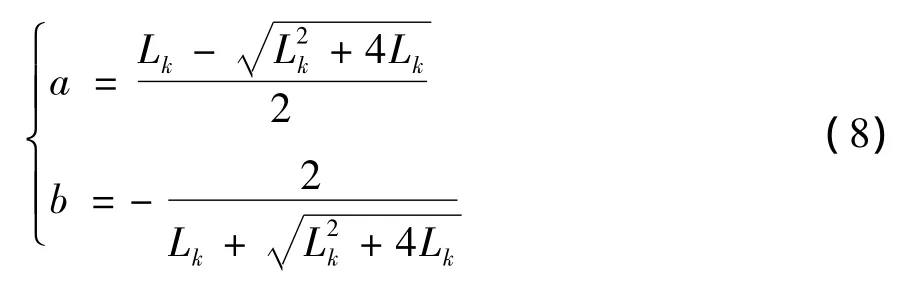
由此可得:

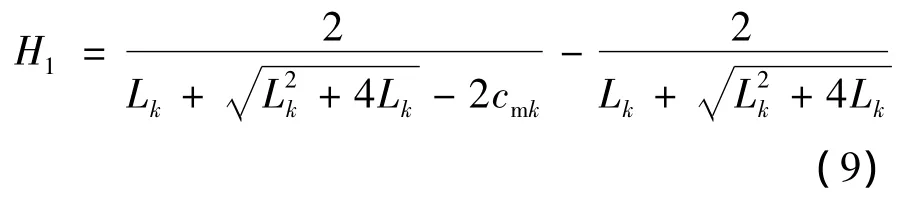
(2)由瓦斯浓度引起的不安全程度

根据煤矿开采工作中的实际情况以及《规程》的实际要求，工作面的瓦斯浓度不能超过1.0%，即当瓦斯浓度超过1.0%时，产生警报，且当浓度超过1.5%时应及时断电，为此构造倒数模型:

由《规程》知，当瓦斯的浓度为1.5%时，不安全程度为1;当瓦斯的浓度为1.0%时，不安全程度为0.8，代入模型可得:

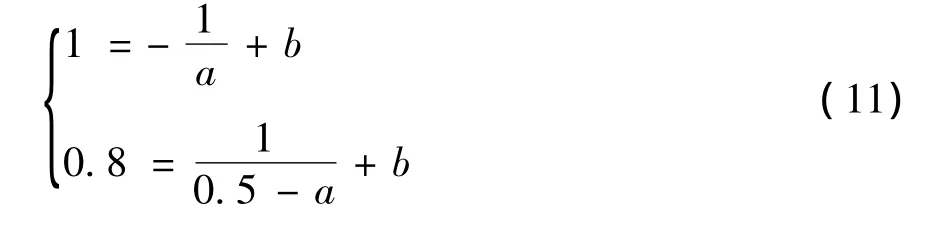
结合实际，求解方程组，得:

由此可以得到模型:

综上所述，当0.8＜H＜1时，警报器发出警报;当H≥1时，不安全程度达到红色危险级别，应及时断电。

2 仿真平台设计与实现

本文选取的小型煤矿环境为一块规则的煤炭待开采区域，上面安置了通风管道;将待开采区域划分为2个采煤工作面，一个掘进工作面，根据《规程》规定在3个工作面、2个回风巷及1个总回风巷上分别安置检测器和报警器，以此作为主仿真登录界面(图1)。

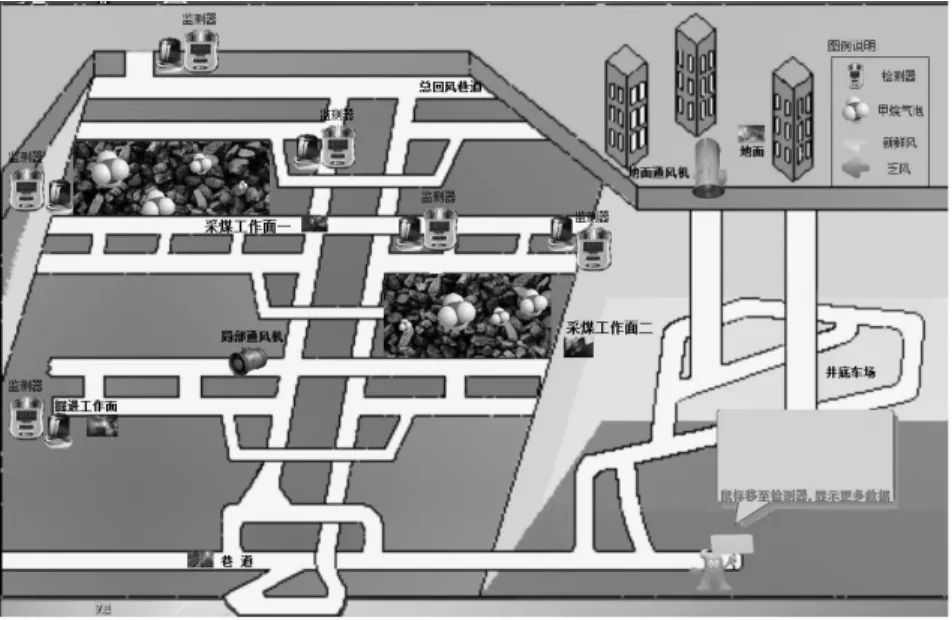
图1 主仿真登录界面

3 结论

本文通过分析，设计了一个小型煤矿安全监测系统，并通过建立瓦斯、煤尘与风速之间的关系，引入矿井的不安全程度概念，建立煤矿安全监测模型，并对数学模型进行求解和仿真。系统仿真界面友好，采用语音报警，各监测点参数实时显示，工作面采用真实图片缩略显示，甲烷气泡代表煤层中瓦斯浓度较大的区域，增加了系统的稳定性和实时性。

［1］马向华，魏震，谢剑英.基于CAN bus的网络控制系统实验平台［J］. 系统仿真学报，2005，17(1):100-103.

［2］He Y，Wang Q G，Lin C，et al.Delay-range-dependent Stability for Systems with Time-varying Delay［J］.Automatica(S0005-1098)，2007，43(2):371-376.

［3］方路平，刘世华，陈盼，等.NS-2网络模拟基础与应用［M］.北京:国防工业出版社，2008.

［4］Hua C，Guan X，Shi P.Robust Backstepping Control for A Class of Time Delayed Systems［J］.IEEE Transactions on Automatic Control(S0018-9286)，2005，50(6):894-899.