基于矩阵变换器的400Hz单相交流电源

吴胜华，赖向东，张显才

（空军预警学院黄陂士官学校，湖北 武汉 430345）

引言

矩阵变换器（MC-Matrix Converter）已广泛应用于交流传动领域。近年来在变频电源方面的研究已逐渐地引起了人们的关注[1-5]。然而，MC的关键技术是功率双向开关的安全换流[6，7]。人们已研究了多种换流控制策略，均是基于输出电流的方向以确定换流的步骤[8]。本文针对SPWM技术及MC变频电源的特点，提出了一种新的门极驱动策略。该方案完全满足MC双向开关的约束条件，不需要提供负载电流或功率器件管压降的任何信息，只要正确地安排同一输出相各双向开关的驱动时序，当某个双向开关关断时，其它相关双向开关便自动提供续流通道。克服了因感性负载瞬间开路而引起的固有电压过冲，保证了双向功率开关的安全。文章详细介绍了智能型自然换流及MC SPWM单相400 Hz交流电源的工作原理，并给出了仿真和实验结果。

1 31MC SPWM控制策略

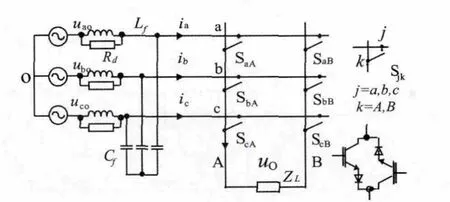
图1 主电路拓扑

三相/单相MC 400 Hz交流电源主电路拓扑如图 1 所示。 图中 uao、ubo、uco为三相交流输入，uo为单相400 Hz 220 V输出(滤波后)。根据MC间接变换原理[5]，可以将MC虚拟为“整流”和“逆变”两个环节。“整流环节”产生虚拟的“直流高压”，“逆变环节”则根据输出的需要对频率和幅值进行变换，以得到预想的正弦交流电压输出。设MC三相输入为

式中：Uim为相电压幅值；ωi为输入电源的角频率。若整流环节理想开关函数为

则虚拟直流电压为

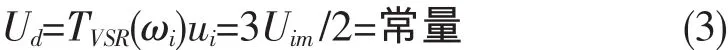
单相逆变环节理想开关函数为

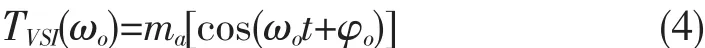
式中：ma为调制系数；ωo为输出电压的角频率；φo为初相角。MC输出电压为

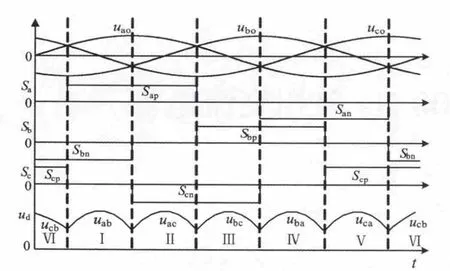
图2 整流开关函数及扇区划分

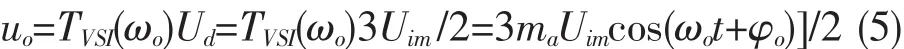
显然，式（3）表示电压型整流器（VSR）的工作原理。式（5）则表示电压型逆变器（VSI）的工作原理。

工程实现时将输入电压一个周期划为6个S型扇区[9]。每一相整流开关函数Sj(j∈a,b,c)可分解成两个子函数 Sjp、Sjn，如图 2所示。

按照二极管不控整流原理，图中Ud即为虚拟直流高压波形。整流开关函数是在不同的扇区选取不同的Sjk组合成逆变器投入工作。MC的输出端便可得到SPWM高频脉冲输出，滤波后即为所需频率和幅值的交流电压。其中一个双向开关Sjk的2路驱动信号 gjk1、gjk2可表示为

式中：uSPWMi（i=1，2）为其中一路参考正弦的脉宽调制信号，为其逻辑非。

2 31MC自然换流原理

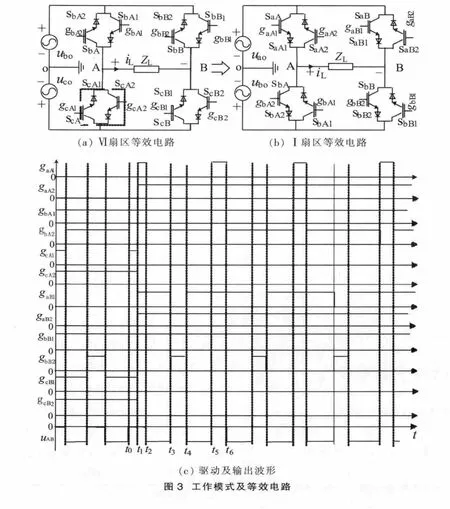
下面以感性负载为例参照图3并以gaA1的时序为基准分析其自然换流原理。分析之前作以下基本假定：①输入为对称三相交流电压；②为具有一般性，考虑死区时间td（图中未能表示出）；③开关频率远高于输入电源频率，一个开关周期内的输入电压可视作常量；④忽略功率器件的管压降。且约定高电平开通，低电平关断；⑤iL及uAB（未滤波）约定极性如图所示。

（1） t0～t1，扇区Ⅵ，等效电路图 3（a）

t1之前，uco＞ubo，uao过零，uco、ubo为 MC 供电，双向开关 ScA、ScB、SbA、SbB组成的 H 桥。 gbA1高电平，因串联二极管反偏，SbA1关断；gbA2低电平，SbA2关断，则SbA关断。 同理 SbB也关断。 gcA1、gcA2及 gcB1、gcB2高电平，ScA、ScB可以为iL提供两个方向的续流通道。按约定极性 iL经 ScA1，ScB2续流。 uAB=0。

（2） t1～t2，扇区Ⅰ，等效电路图 3（b）

t＞t1，gcA1、gcA2及 gcB1、gcB2为低电平，ScA、ScB关断，SaA、SbA、SaB、SbB组成 H 桥。MC 退出扇区Ⅵ，进入扇区Ⅰ。 gbA1、gbB1、gaA1、gaB1、gaB2、gaA2均为高电平。 只有 gbB2、gbA2为低电平，SbA1、SbB1反偏， 则 SbA、SbB截止。 iL由SaA1、SaB2续流。 t1～t2期间 uAB=0。

（3） t2～t3，扇区Ⅰ，等效电路图 3（b）

t2～t3，uao、ubo为 MC 供电。 t＞t2，gaA1低电平，gaA2虽高电平，但SaA2反偏截止，则SaA关断。td期间iL由SbA1、SaB2（或 SbB1、SaA2）向交流电网反馈。td之后，gbA2高电平，gaB1（2）时已为高电平，则 SaB1、SbA2零压零流开通，uAB=-uab。iL则继续沿原路经向电网反馈（如此时iL反向则 SbA1、SaB2零压零流关断）。

（4） t3～t4，扇区Ⅰ，等效电路图 3（b）

SaA维持截止。 t＞t3gaB1低电平，SaB1零压零流关断。td期间，iL的路径及方向不变（如（3）中 iL已反向则经 SbB1、SbA2续流）。 td之后，gbB2高电平，SbB2开通，iL经 SbA1、SbB2（或由 SbB1、SbA2）续流。 uAB=0。

（5） t4～t5，扇区Ⅰ，等效电路图 3（b）

t＞t4，gbB2低电平，SbB2关断。 td期间，iL经 SaB2、SbA1（或 SbB1、SaA2）继续向电网反馈。 td之后，gaB1高电平，SaB1、SbA2再次零压零流开通。 t4～t5期间 uAB=-uab，iL的方向路径不变。至此MC的一个开关周期结束，其间MC输出两个SPWM脉冲。MC输出到滤波网络为常规单极性SPWM脉冲序列。分析可得

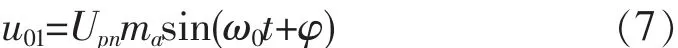
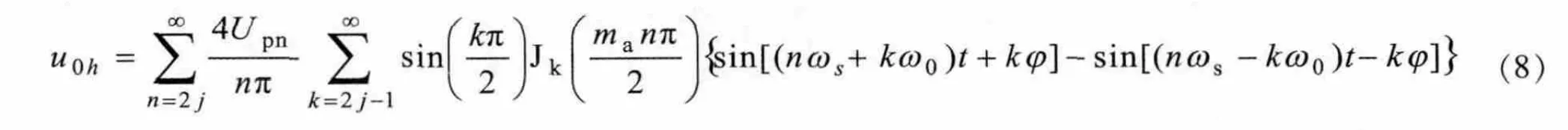
式（7）为基波分量，式（8）为谐波分量。式中Jk（x）为 k 阶贝塞尔级数，谐波分布规律为 nωs±kω0，即各组以nωs为中心边频±kω0两边对称分布。其中n为谐波分组序号，k为谐波次数序号。谐波幅值(4Upn/nπ)Jk(nπma/2)。最低组谐波为 2ωs±kω0，保留了单相逆变器单极倍频的优点。

3 仿真与实验

仿真的主要参数为：三相220 V/380 V/50 Hz对称输入。 Lif=500 μН，Cif=10 μF，Rd=100 Ω。载波频率 fs=15 kHz， 调制频率 fr=400 Hz，mc≈0.66，td≈2.2 μS。 输出滤波 Lof=0.5 mH，Cof=20 μF（图 1 中未表示出）。 输出400 Hz，220 Vrms。S≈4 kVA。 图4为仿真结果。其中图 4(a)、(b)、(c)与图 4(d)、(e)分别共一个时间轴。图4(a)、(b)分别为双向开关SbA两端及MC的输出电压uAB波形。图4(c)为uAB滤波后的输出波形，THD≈2.4%。图4(d)为uAB的展开波形。仿真电路中并未采取缓冲措施，可以看出脉冲波头整齐干净无电压过冲毛刺。说明该换流策略效果理想。图4(e)为SbA的电流波形。图(f)为uAB的频谱，第一组谐波的中心为30 kHz，与式（8）表示的倍频特性相一致。

实验样机的功率双向开关Sjk采用IGW60T120 IGBT及DSEI 60-12A快恢复二极管组成。实验参数与仿真参数基本相同，ma≈0.71，感性负载，阻抗角φ=56.71°。图5为电路实验的部分波形，输出波形uo的THD=2.9，io为负载电流。图中其余各波形的意义清楚，不再逐一说明。仿真及实验结果证实了所提方案及其分析是正确的，Sjk的智能换流效果是理想的。若负载与电网需要隔离，可在A、B端插入400 Hz变压器。

图4 仿真波形

图5 实验波形

4 结论

由以上分析可知该换流策略有如下特点：（1）同一条输出线上的双向开关可以设置死区时间td，提高了功率开关的可靠性；（2）无需检测iL及Sjk两端的电压的极性；（3）为承受反压的功率开关Sjk提供高电平驱动，可为iL提供续流通道；（4）MC的输出为常规单极性SPWM脉冲序列，依旧保留了常规逆变器的倍频特点，有利于输出滤波。结果表明，所提方案正确可行。

[1]Ratanapanachote S,Cha H J,et al.A Digitally Controlled Switch Mode Power Supply Based on Matrix Converter[J].IEEE Trans.on Power Electronics,2006，21(1)：124-130.

[2]Zanchetta P,Wheeler P,Empringham L,et al.Design Control and Implementation of a Three-Phase Utility Power Supply Based on The Matrix Converter[C].IEEE IET Power Electron.,2009,2(2)：156-162.

[3]Katsis D，Wheeler P，Clare J，et al.A Three-Phase Utility Power Supply Based on the Matrix Converter//[C].IEEE IAS’04，2004：1447-1451.

[4]Idris Z，Hamzah M K.Implementation of a new Single-Phase Cyclo-converter based on Single-Phase Matrix Converter Topology using Sinusoidal Pulse Width Modulation with Passive Load Condit[C].IEEE ICIEA，2006：1-6.

[5]Babaei E，Hosseini H S，Gharehpetion G B.Reduction of THD and low order harmonics with Symmetrical output current for single-Phase ac/ac Matrix Converters[M].Electrical Power and Energy Systems，2009：1-11.

[6]Khai NM，Jung YG，Lim YC.A Single-Phase Z-Source Cyclocon- Verter （SPZC）Based on Single-Phase Matrix Converter（SPMC）Topology with safe Commutation Strategy.International Symposium on Electrical and Electronics Engineering[C].2007：205-211.

[7]I Dris Z，Noor S Z M，Hamzah M K.Safe Commutation Strategy in Single Phase Matrix Converter[C].IEEE PEDS 2005：886-891.

[8]孙凯，周大宁，梅杨.矩阵式变换器技术及其应用[M].北京：机械工业出版社，2007.

[9]吴保芳，权建洲，吴胜华，等.非正常输入条件下SPWM矩阵变换器的前馈补偿控制[J].电工技术学报,2005,20(12)：25-29.