基于Ansoft新型交直流混合供电系统接口变压器仿真研究及解决因直流引起的磁饱和问题的措施
柏 海 ,易灵芝 ,董鹏飞 ,王 江 ,陈鸿蔚 ,蒋 鹏
(1.智能计算与信息处理教育部重点实验室(湘潭大学),湖南 湘潭 411105;2.湘潭牵引电气设备研究所有限公司,湖南 湘潭 411101;3.湘潭电机股份有限公司,湖南 湘潭 411101)
引言
三相四线制是低压配电网中最主要的供电方式,在三相四线制系统中,因三相负载的不对称而产生的不平衡电流,尤其是零序电流,严重时会引起电网内电压和电流的不平衡,增加线路及变压器的铜损、铁损,降低变压器的出力,甚至会影响变压器的安全运行。目前抑制零序电流的主要方法是采用 Zigzag变压器,针对该类变压器展研究,具有一定的社会经济价值。
文献[1]指出Zigzag联结在减少三相零序性电流在中性线上,叠加带来的“相位差”导致的危害中有着很大的作用。文献[2]提出在AC-DC电源传输转换双回交流输电线路中采用Zigzag联结,避免由于直流电流流动导致变压器饱和。文献[3]充分发挥Zigzag变压器在治理零序谐波方面的优势,研发Zigzag变压器与APF相结合的新型滤波装置。文献[4]对Zigzag变压器进行建模,进行三相不平衡负载、三相不平衡电源及作为整流变压器应用的3种情况下仿真实验,在三相不平衡运行时Zigzag变压器可以相互补偿铁芯的磁通量,最大限度地控制各相感应电动势的一致性,从而持三相平衡,降低零线电流。
目前,关于Zigzag变压器的研究,都集中在:三相四线制系统中能降低零序电流。本论文探讨三绕组D—Z型联结变压器模型及等效电路分析、磁路分析、基于Ansoft仿真变压器的磁路分析及其在三相四线制系统中的实际应用。
1 Zigzag变压器磁路分析
1.1 Z联结原理
Zigzag变压器采用曲折形联结,也称结Z联结,就是把每相绕组分成两半,分别套在两个铁心柱上,然后倒接串联,也就是说每个铁心柱上都套有分属于两个相位不同的绕组,如图1所示。图1中(a)为三相绕组Z联结的接线方式;(b)为相量图。这种结线方式各相下半截线圈在左边的铁心柱上,称为左行联接。如果反过来下半截线圈在右边铁心柱上,则称为右行联结。左行和右行的区别是,相量U˙A、U˙B、U˙C都向同一方向旋转 60°,但相互之间的相位差仍然都是120°,相位顺序也不变。
鉴于三角形联结能有效衰减三次谐波,而曲折形联结在治理零序谐波方面有独特的优势,使得整套装置具有较高的性价比和广阔的市场应用前景。因此本文研究的三绕组变压器的接线方式为:变压器一次侧采用三角形联结,二次侧采用曲折形联结,接线方式见图2。
1.2 三相Zigzag变压器的等效电路
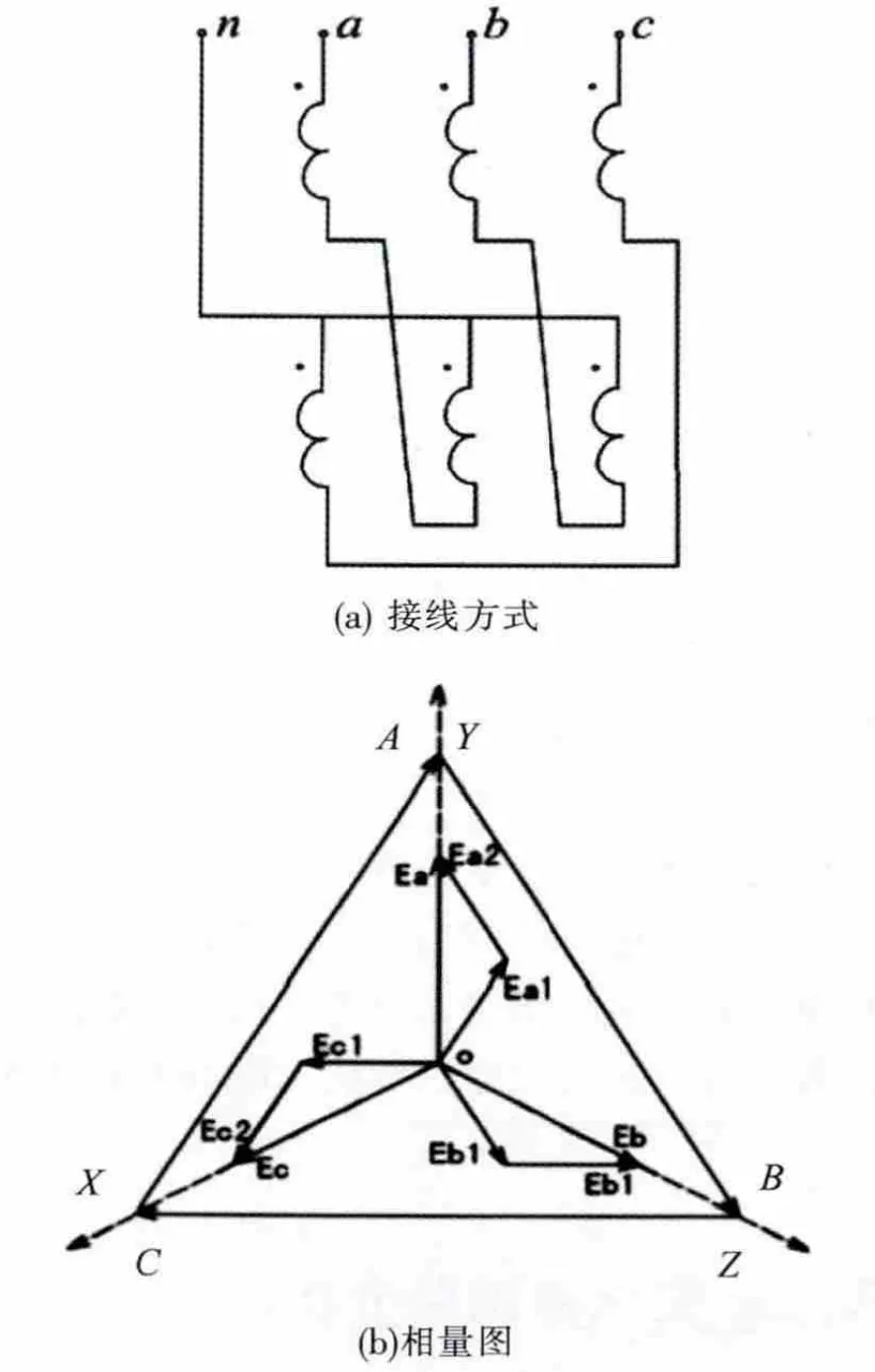
图1 Zigzag变压器连接与相应相量图[8]
通过分析单相三绕组变压器T形等效电路,列写数学方程,得到绕组端电压、电流与变压器各励磁参数的关系,用于工频量和暂态量的分析和计算。研究发现:三绕组变压器的等效电路和双绕组变压器等效电路形式基本一样,只是铁芯柱上多了一个绕组。同理,更容易分析三相三绕组变压器的等效电路[5]。三相三柱式变压器新的数学模型概念清晰,等效电路模型,反映各电流在感应绕组端电压中所起的作用,易于分析和计算。因为三相电路完全对称,所以由单相三绕组等效电路,可得到三相三绕组等效电路[7],见图3。

图2 D-Z接线方式

图3 三相D-Z变压器等效电路


原边电压EA满足:

设移相角为γ,则
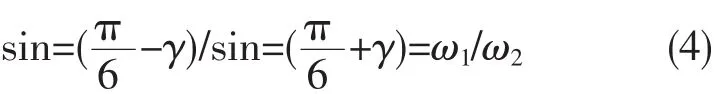
当ω2=ω3时,由其接线方式可得:

式中:LPA、LPB和LPC分别为对应同时交链芯柱A、B和C两侧绕组漏磁通的电感;LAB、LAC和LBC分别为芯柱A与芯柱B、A与C、B与C绕组的互感;Ida、Idb、Idc分别为芯柱 A,B,C 绕组差流;r1、r2、r3分别为简化等效电路的等效电阻。
2 基于Ansoft 12的Zigzag变压器有限元分析
Ansoft Maxwell软件是完全的Window程序,友好的用户界面,使用起来直观、方便。该软件较比其它有限元分析软件具有如下几点优势[6]:① 具有强大的数据处理功能。②拥有简便易行的绘图功能的同时兼有模型输入端口,可以方便的导入其他绘图软件形成的模型。③在剖分过程中,可进行手动剖分和自动剖分,网格形状和疏密程度灵活多样,能量误差可减小到任意指定值。④能够进行各类线性和非线性分析。
2.1 变压器建模
基于D-Z型连接方案,建立Zigzag变压器的Maxwell2D 模型[4],见图 4。
2.2 Zigzag变压器模型外电路连接
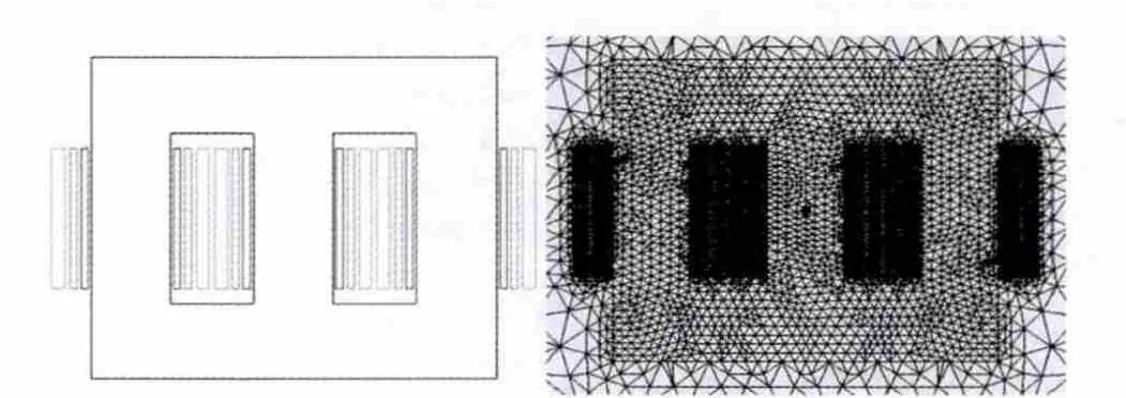
图4 Zigzag变压器Maxwell2D模型和网格剖分

图5 Zigzag变压器原边外电路

图6 2、3次侧外电路
由于Maxwell 2D内部直接向模型上施加电源比较模糊,可以在瞬态场中,采用导入外电路的形式,实现变压器模型一次侧的控制电路,其中A、B、C各相均采用110 kV交流电压源,原边绕组三角形联结。
采用曲折形联结,绕组上的点表示绕组电流的流入端。2次侧加上一个纯电阻负载,3次侧中性点接地,见图6。
在采用高压水力冲刷清淤时必须根据现场实际情况(管径、淤积程度和管渠形状等),选择合适的喷头、冲洗压力(70~140 Bar)和冲洗流速。若沉积物特别密实,则需要采用铣床钻头进行清理(见图1)。
对同一周期内(T=0.02~0.04 s)BC铁芯柱、CA芯柱、AB芯柱的磁力线分布情况进行仿真实验。可以看出随着绕组铁心交链励磁,变压器各个铁芯柱之间磁力线在不断有规律的变化。铁心中既有在铁芯柱内部闭合的主磁通,也有仅与某一绕组交链的主要经空气等非磁性物质闭合的漏磁通,见图7。
同样,通过对同一周期内不同时刻的磁场强度分布进行仿真实验,可以发现:不同铁芯柱上的磁场强度随时间变化而出现强弱不同的情形,在交流电压不断变化的同时,场强也随之变化,见图8。

图7 T=0.029 s和0.032 s时的磁力线分布
因为Zigzag变压器三相参数完全对称,故以A为例,观察其一、二、三次侧绕组电压之间的关系,见图9, 可以看出,a2与A 相差30°,a2与 a1相差60°,正好符合曲折形联结的电压相位关系;a2=a1,波峰值约为107 kV,A波峰值约为188 kV,接近a2的倍,符合曲折形联结的电压幅值关系,验证了所建模型的正确性。

图8 T=0.029 s和0.032 s时的场强分布
根据图9和表1,从电压波形曲线到电压数据表,能直观看到各相一、二、三次侧绕组电压之间的关系(因此三相对称,所以B、C相的结果与A相相近,略去)。 即:
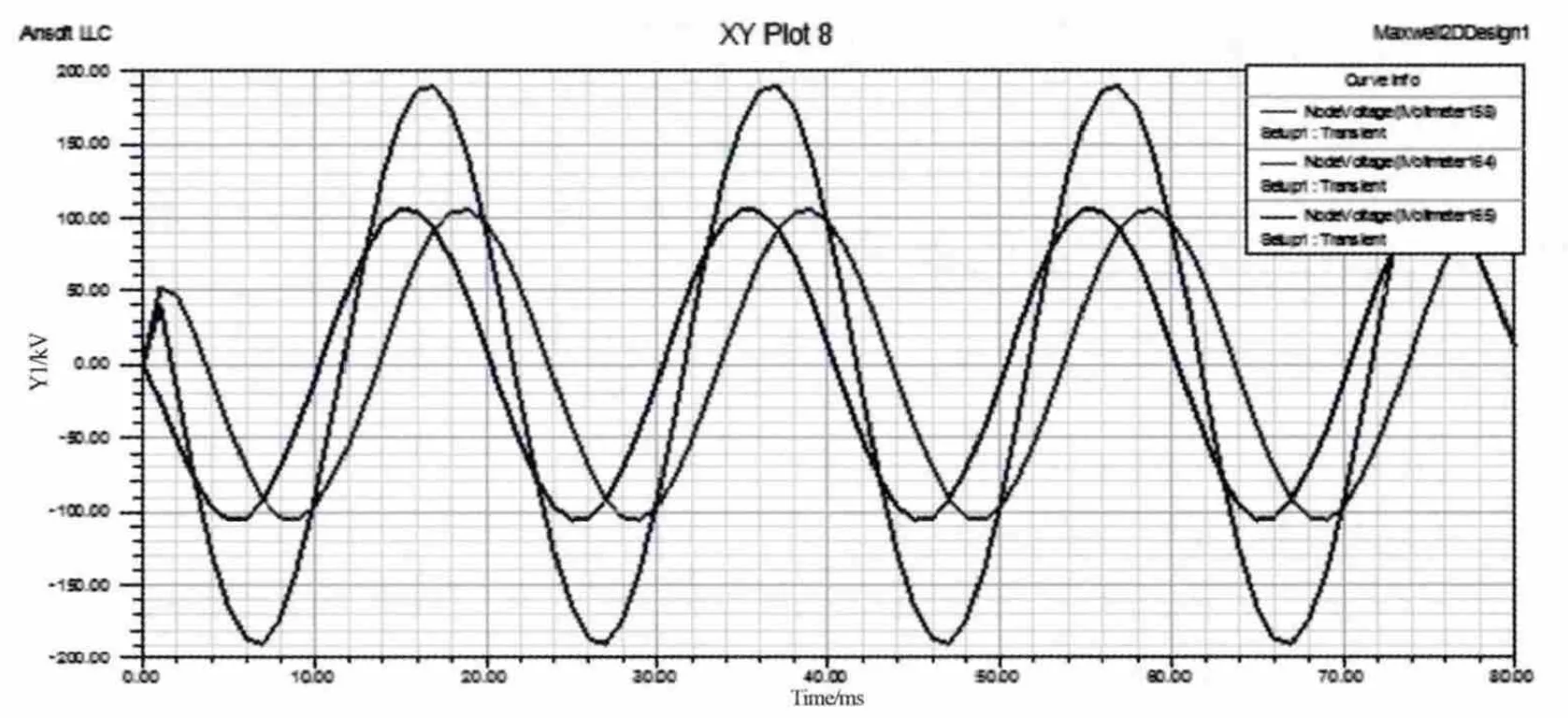
图9 A相一、二、三次侧绕组电压曲线

表1 A相电压数据表

3 Zigzag变压器的应用
3.1 三相不对称负载情况
三相系统的电压对称,均连接110 k V电压源,频率为50 Hz,负载为电阻性负载,A相电阻为139.2 Ω,B相和C相电阻都为69.6 Ω。采用Zigzag变压器进行仿真,观察中性电流。一次侧电路见图5,二、三次侧电路如图6。图10用 Zigzag变压器给三相不平衡负载供电时的中线电流,通过仿真可知在负载不平衡时,Zigzag变压器下的中性点电流为0。
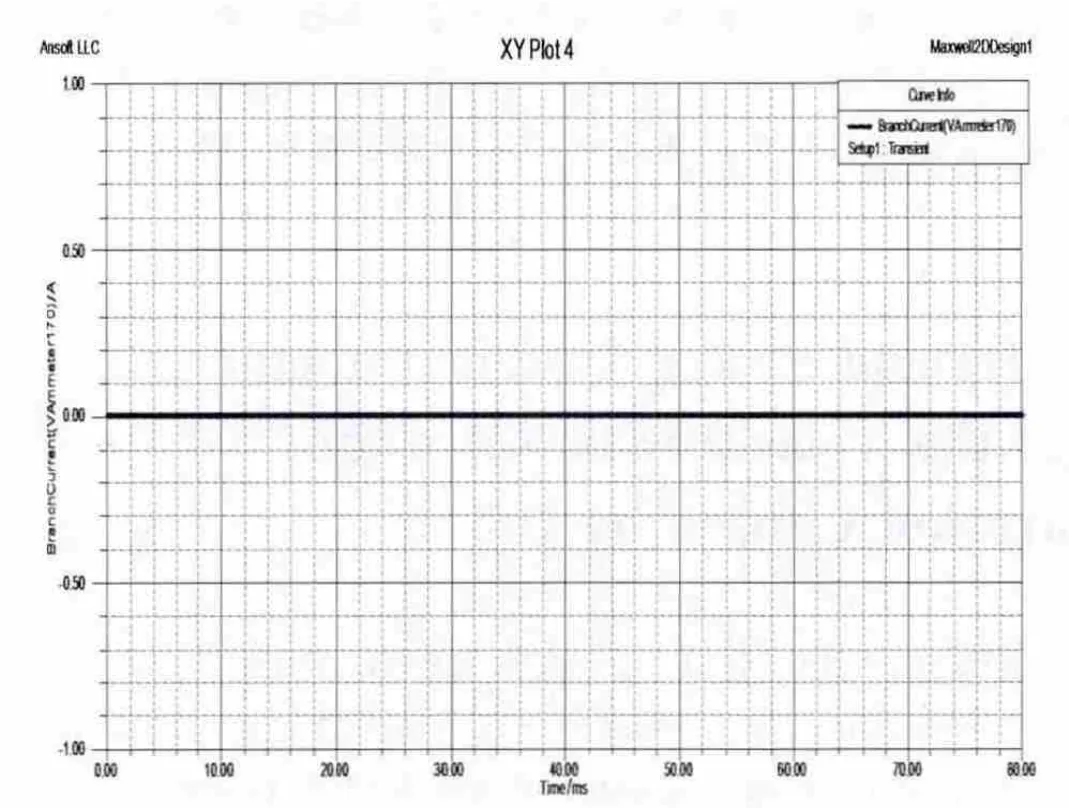
图10 Zigzag变压器供电时的中线电流


3.2 三相不对称电源情况
三相电源分别为初相位为 0°、-120°、+120°,A、B相电压源为110 kV,C相电压有效值为55 kV,频率 50 Hz,负载均为 25 Ω电阻性负载,采用与3.1相同的仿真电路,观察其中线电流。二、三次侧电路见图6,一次侧电路如图5。用Zigzag变压器在三相不平衡电源情况给负载供电时的中线电流,通过仿真可以知道在电源不平衡时,Zigzag变压器下的电流幅值明显减小,即可以减少相应影响。
从图11和图12可以看出注入直流电流后主磁力线变化并不大,漏磁力线减少,由于该变压器三相完全对称,故其电流矢量在中性点处相互抵消,即电流矢量和为零,因此其在中性点处的电流为0。
4 结语
在一般变压器等效电路模型基础上进行扩展,建立三相三柱三绕组变压器数学建模,得到三绕组变压器的等效电路。利用Ansoft Maxwell软件对三绕组D—Z型联结变压器建立变压器内部结构模型,观察该变压器的磁场强度、磁力线、电压电流波形。将Zigzag变压器应用在三相不对称负载和三相不对称电源系统2种情况下,以及交直流混合供电系统中,使因直流引起的磁饱和问题得到有效解决。仿真结果表明:
(1)△接法能有效衰减三次谐波。
(2)D-Z接法提供三相四线制电源不平衡电流回路,能降低由不平衡负载所造成的影响。
(3)鉴于该变压器零序性电流阻抗很小,因此能降低系统中性线的电流含量,使三相对称。
(4)当在副边绕组的中性点上注入直流时,同一铁芯上的两个绕组的直流磁势相互抵消,从而避免了因直流引起的磁饱和现象和一次侧励磁电流的畸变,减小了漏抗。
[1]KAMATH G,MOHAN N,ALBERTSON D.Hardware imple-mentation of a novel reduced rating active filter for 3-phase,4-wire loads[C].Proceedings of the Applied Power ElectronicsConference and Exposition,Dallan,USA:IEEE,1995:984-989.
[2]B H Khan,K P Basu.Stability Improvement of Power System by Simultaneous AC-DC Power Transmission[J].Electric Power System Research.2008,78:756-764.
[3]庞师锋,王莉娜.三相四线制系统新型中线滤波装置研究[J].电力电子.2008(4):40-43.
[4]周鹏,郭忠文.Zigzag变压器的建模与应用[J].电力自动化设备,2007(12):93-95.
[5]索南加乐,等.基于磁路特征的三相三柱式变压器数学模型及等效电路[J].电力系统自动化,2011(15):52-57.
[6]赵博,张洪亮.Ansoft 12在工程电磁场中的应用[M].北京:中国水利水电出版社,2010.
[7]柯广,易灵芝,等.基于双回路交直流同线输电方式线路增容研究[J].电力系统保护与控制,2013,46(6):25-31.
[8]唐介.电机与拖动[M].北京:高等教育出版社,2007.

