一种新颖的三相高频链矩阵式逆变器的控制方法研究

李 黎 ，黄 鑫 ，黄金波

(1.重庆市电力公司城口供电公司，重庆405900；2.浙江省电力公司嘉兴供电公司，浙江 嘉兴 314033）

引言

自1977年Mr.Espelage和Mr.Bose提出了高频链逆变技术的新概念后[1]，三相高频链逆变技术以其重量轻、体积小、功率密度大和可靠性高等优越的性能，在分布式供电系统、新能源发电并网以及UPS供电系统等需要电气隔离的场合中得到广泛的应用。但是，这类逆变器有一个固有的缺点，采用传统PWM技术的后级矩阵变换器在器件换流时打断了高频变压器漏感中连续的电流，于是在高频变压器和矩阵变换器之间造成不可避免的电压过冲。为了实现后级矩阵变换器的安全工作，国内外学者先后提出了多种换流方法，比如自然换相法[2]、重叠换相法[3]、移相控制ZVS法[4]。文献[5]从分析矩阵式变换器拓扑结构入手，提出一种解结耦思路，将其解耦成2个常规的三相电压源逆变器，降低了后级矩阵变换器的控制难度。文献[6]基于此思路，提出了一种SPWM调制策略，但在换流过程中依然存在电压应力过高的问题。

本文就三相高频链矩阵式逆变器的电路拓扑，运用解结耦思路，提出一种SPWM混合调制策略。对构成双向开关的两个单向开关器件不采用移相调制策略中的同步驱动方式，而是分别进行独立控制。通过对单向开关管施加相应的逻辑驱动信号，利用反并联二极管，为负载电流提供续流通路。从而把矩阵变换器的换流问题演化为传统三相半桥逆变器的换流问题，无需添加额外的辅助检测环节，有效解决换流问题，实现一步自适应换流。文中详细分析了高频交流周期内变换器的工作状态。通过对常规SPWM波形进行简单的逻辑处理，即可得到矩阵变换器的12路单向开关器件驱动信号。最后搭建了一台实验样机，实验结果验证了该策略的可行性。

1 电路工作原理

1.1 控制方法

图1 是三相高频链矩阵式逆变器的主电路拓扑，主电路采用DC/AC1/AC2两级功率变换方式。高频变压器隔离输出前级逆变产生的高频交流方波，作为后级矩阵变换器的输入。按照拓扑解耦控制方法[5]，根据高频交流方波的极性将后级矩阵变换器分解成两个常规三相电压源逆变器，如图2所示。当高频逆变桥输出正极性高频方波时，将可以正向工作的逆变器定义为正组。反之，将可以负向工作的逆变器定义为负组。

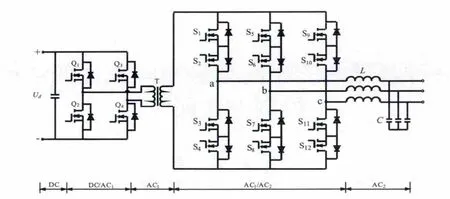
图1 高频链矩阵式逆变器主电路拓扑

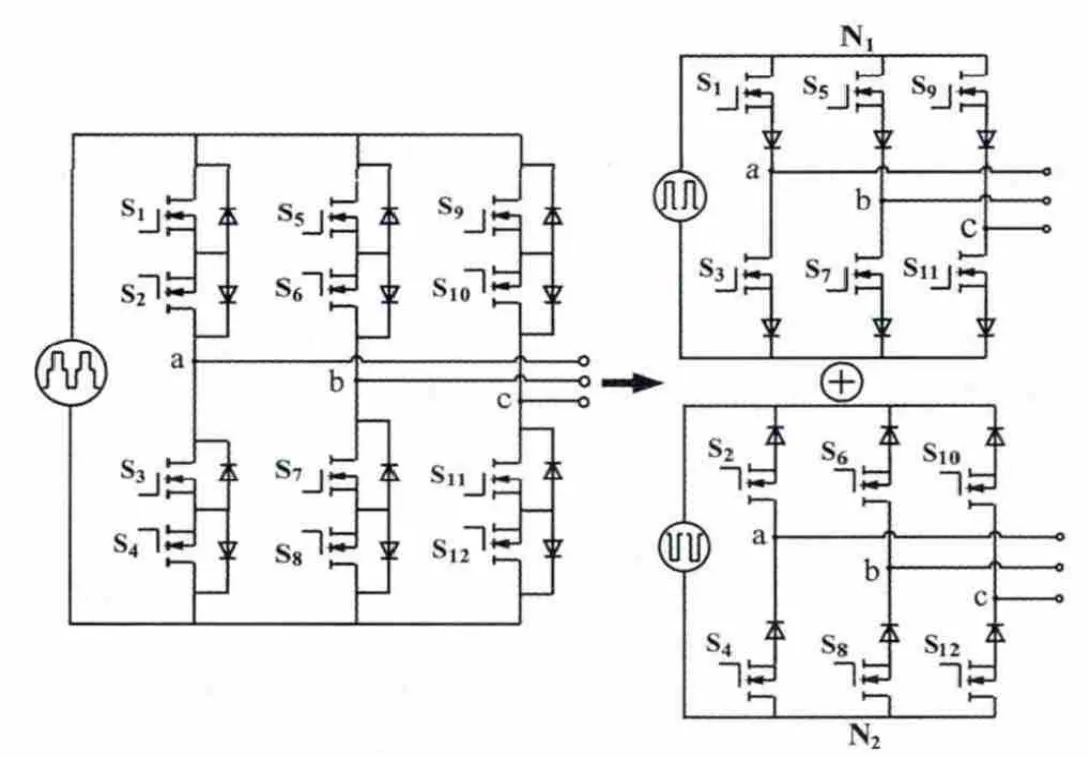
图2 矩阵逆变器的解结耦

按下述原则进行控制，既可获得与传统的三相电压源型逆变器基本相同的输出电压效果，也可有效解决矩阵变换器的换流问题，实现一步自适应换流，如图3所示。

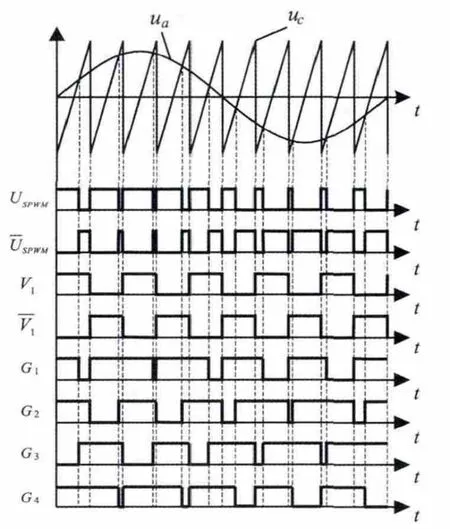
图3 双向桥臂开关驱动信号

（1）当矩阵变换器输入为正极性时，触发负组逆变器N2的所有开关，正组逆变器N1按照常规SPWM调制方式正常工作。

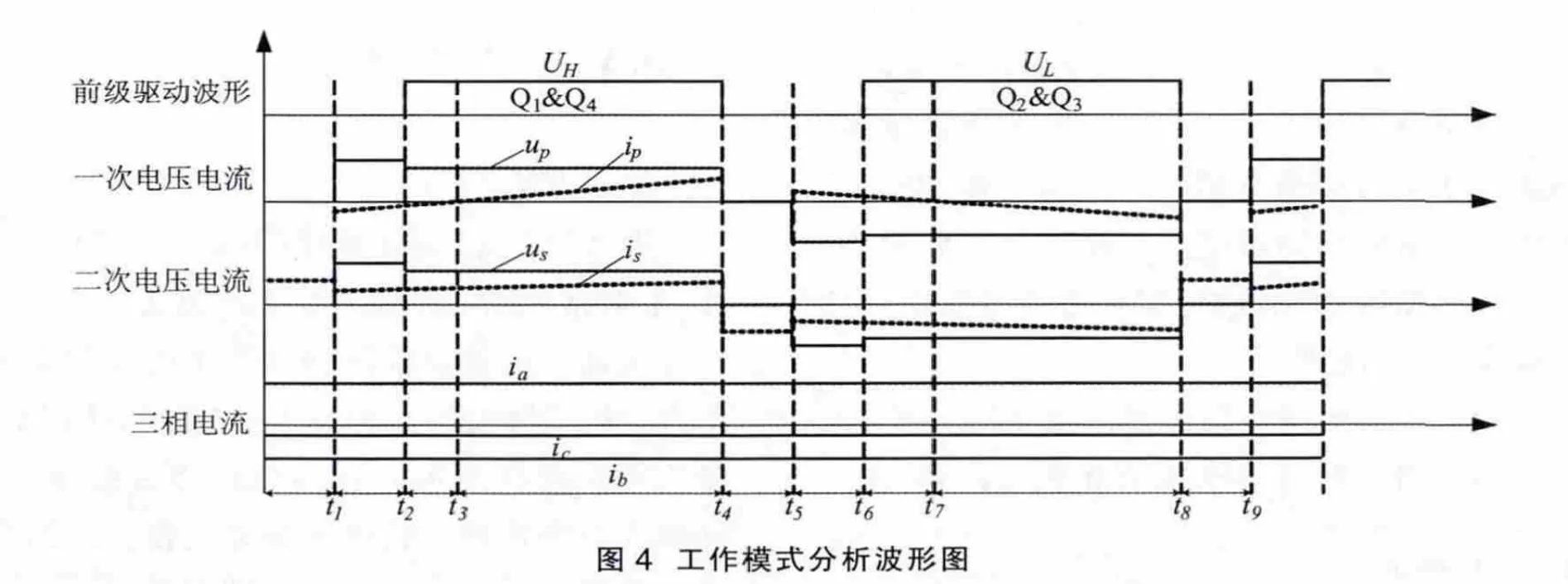
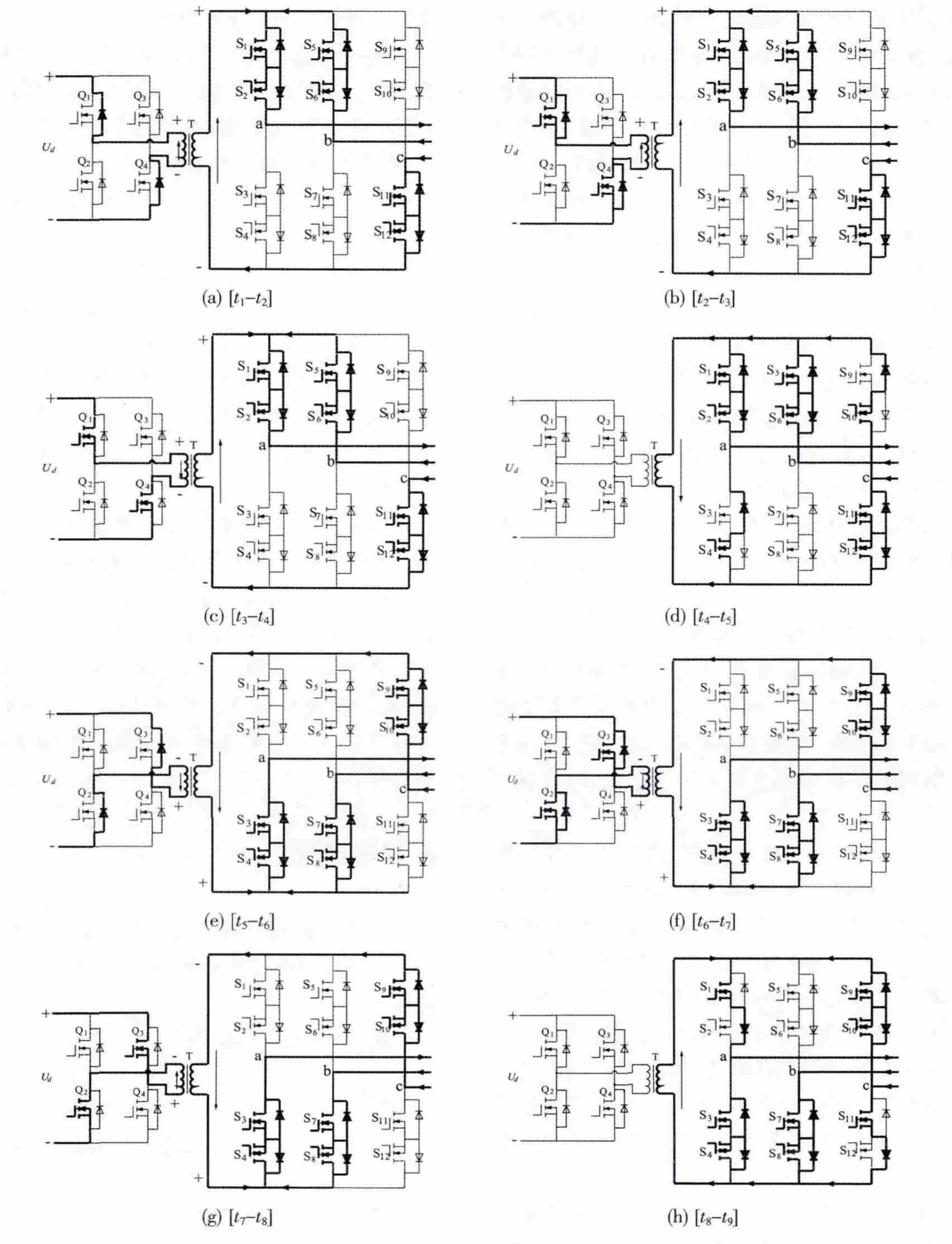
图5 主电路工作模式

（2）当矩阵变换器输入为负极性时，触发正组逆变器N1的所有开关，负组逆变器N2按照常规SPWM调制方式正常工作。

1.2 电路工作过程分析

在前桥逆变器的一个高频交流周期内，对主电路的工作状态进行分析，波形图如4所示。UH、UL分别为前桥逆变器上、下桥臂的驱动信号。把一个高频交流方波周期分为8个工作阶段，其中t3、t7时刻为高频变压器一次侧电流过零时刻，t1、t5时刻分别为高频交流方波的死区中点。假设在此高频周期内三相相电流的方向分别为：ia＞0，ib＜0，ic＜0；后级变换器在高频交流方波的死区中点进行正、负组逆变器切换，从负组向正组切换的时刻t1开始分析。

[t1-t2]时段（见图5a）：该时段内前级高频逆变器的四个开关管保持关断状态，后级矩阵变换器由原来t1时刻之前的负组逆变器续流状态切换成正组逆变器工作状态。这时候变压器二次侧电流由原来的B、C两相减小为只有C相电流通过，这将引起高频变压器磁通变化，从而在二次侧感生出上正下负的感应电压。此电压耦合至高频变压器一次侧，引起开关管Q1、Q4反并联二极管的导通。前级逆变器处于能量回馈的工作状态，后级矩阵变换器仍处于正常的功率输出状态，二次电流逐渐增大。变压器中存储的能量一部分回馈给直流侧，一部分提供给负载。

[t2-t3]时段（见图 5b）：t2时刻，前级逆变器的 Q1、Q4开关管开通，假如t2时刻，前级的能量回馈状态尚未结束，Q1、Q4开关管就可以实现零电压开通的软开关动作，本例中能量回馈状态未结束。后级矩阵变换器仍处于正组逆变器的工作状态，向负载输出功率。

[t3-t4]时段（见图 5c）：t3时刻，变压器储存的能量释放完毕，能量回馈状态结束，高频变压器一次侧回馈电流反向归零。前级逆变器输入电压、电流同向，直流侧向主电路输入功率。后级的矩阵变换器仍与前一工作状态相同，正组逆变器正常工作。

[t4-t5]时段 （见图 5d）：t4时刻，Q1、Q4开关管关断。前级逆变器处于关闭状态，高频变压器一次侧输入电压为零。同样，二次侧电压也为零，后级矩阵变换器通过负组逆变器开通的开关管处于续流状态，二次电流自然反向。

[t5-t6]时段（见图 5e）：t5时刻，后级矩阵变换器由原来的正组逆变器工作切换为负组逆变器工作，二次侧电流由原来的B、C两相减小为只有C相电流通过，从而在二次侧感生出上负下正的感应电压。此电压耦合至一次侧，引起Q2、Q3反并联二极管的导通。这一时段，前级逆变器处于把变压器中储存的能量回馈到直流侧的能量回馈状态；后级矩阵变换器通过负组逆变器向负载提供能量。

[t6-t7]时段（见图 5f）：t6时刻，前级电路中的开关管Q2、Q3开通。本例中，t6时刻，能量回馈尚未结束，Q2、Q3零电压开通。变压器二次侧电压与电流同向，矩阵变换器向负载输出功率。

[t7-t8]时段（见图 5g）：t7时刻，变压器储存的能量释放完毕，前级回馈电流过零反向，电压电流同向。直流侧向主电路输入功率。

[t8-t9]时段（见图 5h）：t8时刻，前级逆变器四个开关管全部关断，高频变压器一次侧输入电压为零，从而二次侧电压同样为零。矩阵变换器通过正组逆变器构成续流回路，处于续流工作状态，二次电流自然反向。此后将进入下一个高频交流方波工作周期。

从前面对主电路的工作模式分析中，可以看到，当前级逆变器四个开关管关断时，后级矩阵变换器进入续流运行状态。这时候，另一组保持导通的逆变器就为负载电流提供了续流通路，避免了出现负载电流的断路。并且，在一个高频交流方波周期内，矩阵变换器的换流过程，是随着电路状态转换而自适应一步实现的，不需要添加辅助换流用的检测环节。

2 实验验证

为了验证SPWM混合调制策略的可行性，搭建了一台阻性负载的实验样机。实验样机的主要技术指标如下：

输入电压：Vin=48 V；

输出电压：Vo=110V/50 Hz；

输出电流：Io=3 A；

额定输出功率：Po=500 W；

高频逆变器开关频率：fs1=10 kHz；

高频逆变器占空比：D=0.5；

矩阵变换器开关频率：fs2=20 kHz；

高频变压器变比：n1：n2=12：45。

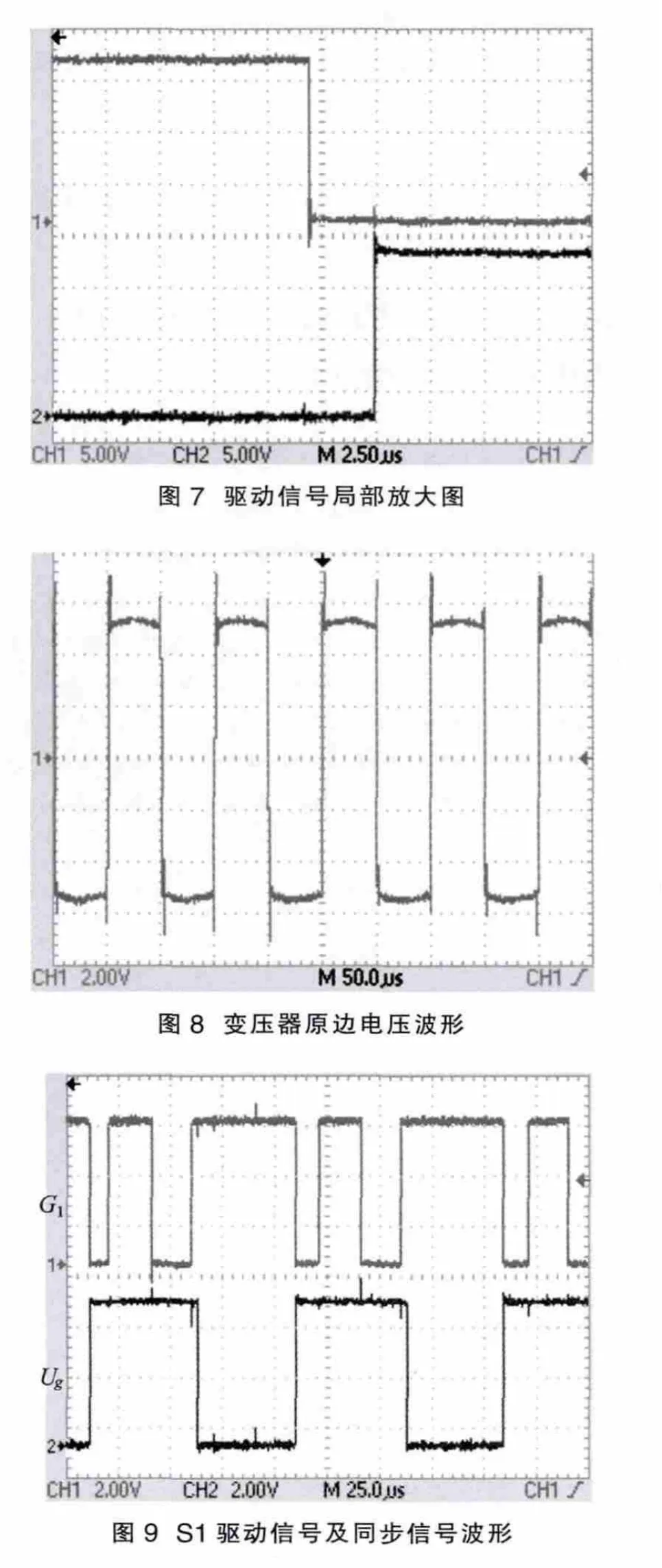
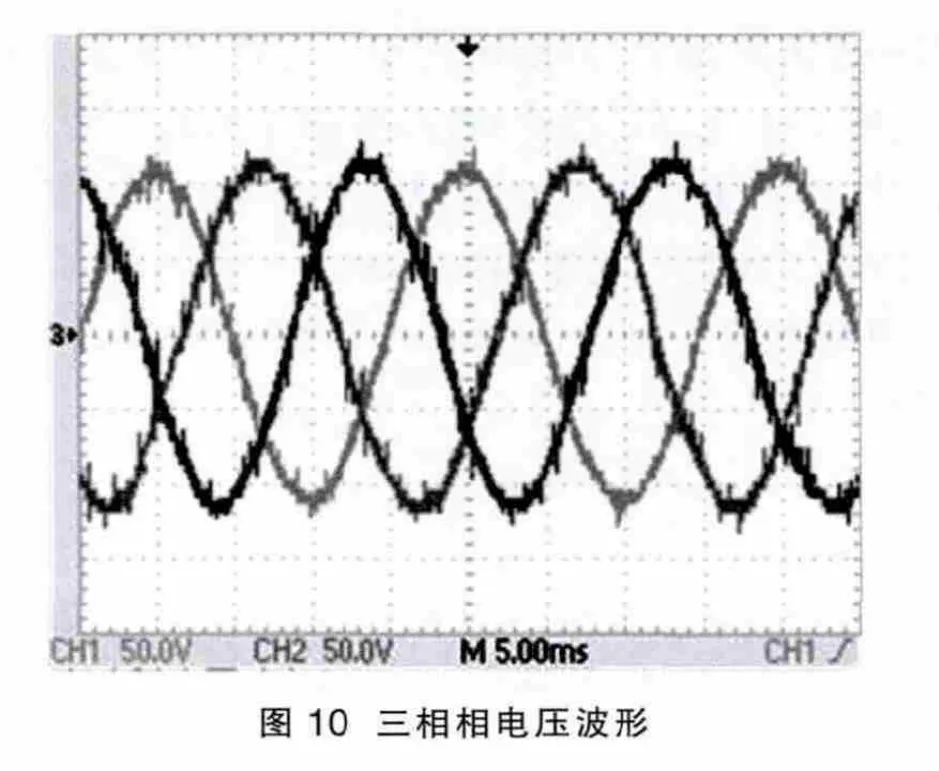
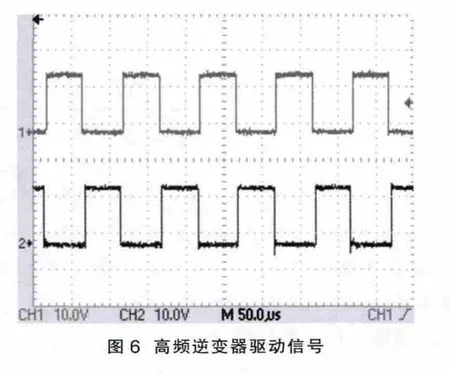
图6 是前级高频逆变器桥臂上下管子的驱动信号波形。在此驱动信号作用下，高频逆变器输出占空比为0.5的双极性高频交流脉冲电压。图7是驱动信号的局部放大图，为了防止桥臂的直通短路现象发生，上下管子的驱动信号设置3 μs的死区时间。图8为输入的48 V直流电压经高频逆变桥逆变后得到的双极性高频交流方波，此电压经高频变压器耦合后作为后级矩阵变换器的输入电压。图9是与双极性高频交流电压脉冲同步的同步信号Ug和矩阵变换器单向开关管S1的驱动信号G1。由图可知，从驱动波形特征上看，在负极性输入电压阶段，管子保持开通；在正极性输入电压阶段，管子按SPWM波形规律进行工作，符合后级矩阵变换器的SPWM混合调制策略的控制要求。本人采用TMS320LF2812DSP作为控制器核心，搭建了一台试验样机。实验系统主要包括以下几个模块：前级单相高频逆变器、高频变压器、矩阵变换器主电路、滤波电路、隔离驱动电路、DSP实验开发板模块。图10为调制比等于0.8时，矩阵变换器带阻性负载输出的110 V/50 Hz三相相电压波形，三相相位对称，幅值和频率都基本正确，但仍含有少量的毛刺电压，需要进一步对滤波参数进行优化。实验结果验证了本文所提电路拓扑和SPWM混合调制策略是正确的。

3 结论

本文针对三相高频链矩阵式逆变器，提出了一种基于拓扑解结耦思想的SPWM混合调制策略，并详细分析了电路系统的具体工作模态。从矩阵变换器的换流角度看，其换流过程是一种自适应一步换流，降低了系统的换流难度，有利于系统安全运行。最后，进行了阻性负载情况下的实验工作，实验结果验证了所提控制策略的正确性与可行性，可望为三相高频链矩阵式逆变器的工程应用提供一定的借鉴。

[1]ESPELAGE P M,BOSE B K.High Frequency Link Power Conversion[J].IEEE Transactions on Industry Applications,1977,13(5)：387-394.

[2]KAWABATA T,HONJO K,SASHIDA N.High frequency link DC/AC converter with PWM cycloconverter[C]//Industry Applications Society Annual Meeting,October 7-12,1990,Seattle,WA,USA.1990：1119-1124.

[3]Matsui M,NAGAI M,NABAE A,et al.High-frequency link DC/AC converter with suppressed voltage clamp circuits-naturally commutated phase angle control with self turn-off devices[J].IEEE Transactions on Industry Applications,1996.32(2)：293-300.

[4]赵永涛,郑连清.单极性移相控制矩阵式高频链逆变器控制方法[J].电源技术,2010,34(03)：284-287.

[5]闫朝阳,李建霞.高频链逆变器之矩阵变换器数学建模与解结耦分析思想证明[J].电工技术学报,2007.22(sup.)：57-63.

[6]郑连清,赵永涛.基于拓扑解耦的矩阵式高频链逆变器控制新方法[J].电力自动化设备,2010,30(8)：41-44.