光伏并网逆变器通用LCL滤波器的设计
赵 明,杨有涛,张 磊,杨 凯,刘伟增
(特变电工西安电气科技有限公司,陕西 西安710119)
引言
伴随着近年来全球光伏发电装机容量的不断增加,光伏并网逆变器的需求量也日益增多,电网电能质量方面的要求迫使光伏并网逆变器在发电质量等方面性能越来越好。滤波器是光伏并网逆变器的重要组成部分,同时也是逆变器提高工作性能的重要环节。
在光伏并网逆变器中,其常用的拓扑结构如图1 所示[1,2],其主要组成部分有:直流断路器、EMI滤波器、逆变桥、滤波器、接触器等。
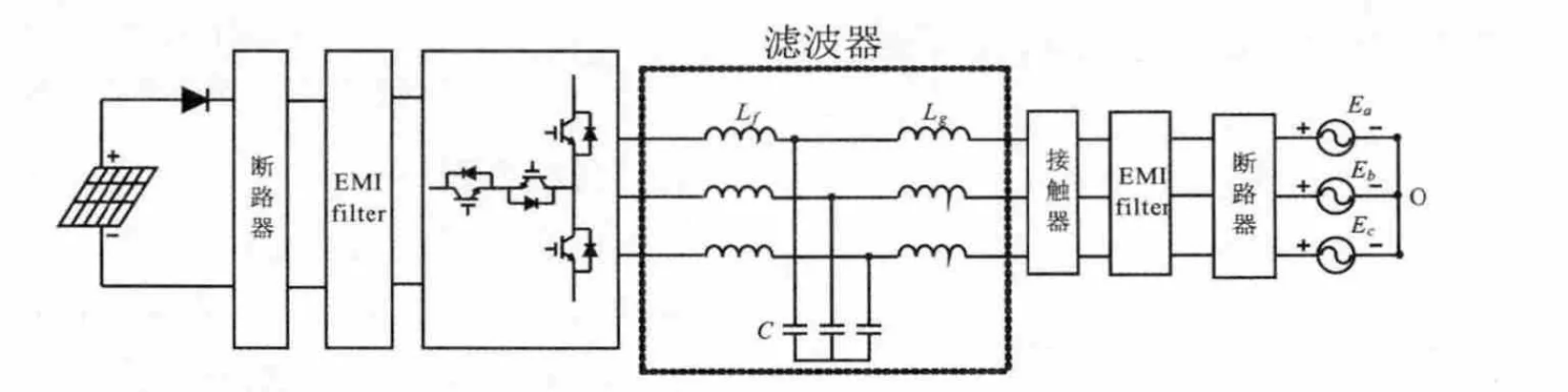
图1 三电平逆变器典型拓扑
本文针对上述常用拓扑结构,对逆变器的工作特点和滤波要求进行了分析,提出了该类滤波器的有效设计方法,同时针对100 kW三电平并网逆变器的参数,设计了LCL滤波器,最后通过仿真验证了该设计的合理性,表明了本文提出的滤波器设计方法的正确性。
1 光伏并网逆变器对LCL滤波器设计的要求
光伏并网逆变器的简化模型如图2所示[2],其主要功能是为电网注入能量,保证注入电流Ig的电能质量。因此对滤波器的要求主要有以下几个方面:谐波、电流纹波、成本、控制系统设计。

图2 逆变器简化模型
1.1 电流纹波方面
输出电流纹波的计算方法在多种文献中提到,在参考文献[3,4]中,电流的纹波公式一般应用于BUCK电路中输出电压被控制的场合,在逆变器中输出控制电流,逆变器的输出电压是电网电压,与输入电压的关系与BUCK电路的公式不同。
逆变器输出电流的纹波主要因为逆变桥开关过程中,电感两端电压VL的不断变化造成的。

在IGBT开通和关断时,VL不同。定义开关函数S:S=1,IGBT 开通;S=0,IGBT 关断。
根据上面定义,根据一般经验以及后面计算可知,Lg电感量一般小于Lf,Lg甚至为线缆电感,因此其压降很小,同时考虑到其输入端有滤波电容,因此可以近似认为VCf电压近似为电网电压,因此可以得到电感Lf两端电压VL的公式为:
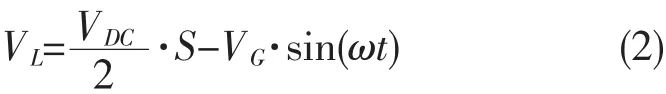
其中,ω是电网角频率。
在光伏并网逆变器中,正常工作时一般要求功率因数为η=0.99,这里可以近似为1。由于控制量与电网相位差φ0很小,对结果影响不大,为便于分析,本文忽略φ0影响,因此:

其中,M是SVPWM发波的调制度,并且满足

联立公式(1)、(2)、(3)可得:
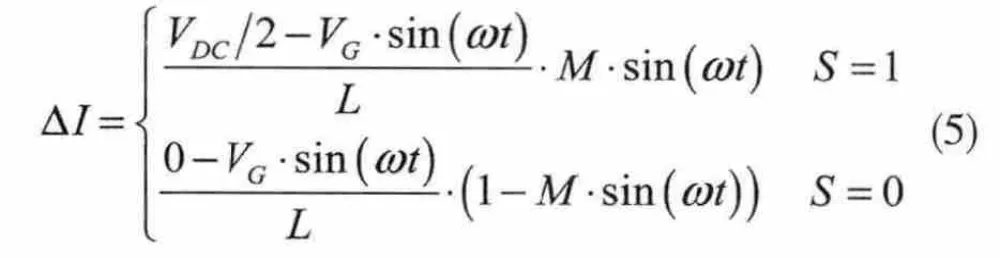
数学推导中,当t满足式(6)时,电流纹波最大值如式(7)所示。

从式(7)可以得出,电流纹波最大值如式(8)所示。
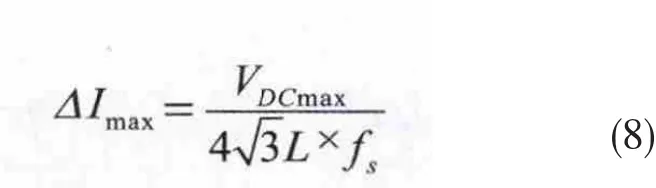
从上面结果可以得出,电流纹波最大值并不是出现在电网电压峰值上,而是随着母线电压的不同而不同,当母线电压为最大值时,纹波电流最大。总输出电流如图4所示。

图3 理论输出电流波形
1.2 谐波方面
根据参考文献[5]国家电网对逆变器的谐波输出的要求为:THD≤5%,并网光伏逆变器必须满足上述要求。降低逆变器谐波的方法一般有两种,一种是通过控制参数及发波的方式降低谐波。另一种是通过合理设计滤波器滤除谐波。本文的方法是针对后者进行设计。
通过公式(8)给出电流纹波计算公式,根据实际需要的纹波电流百分比,可以得到电感的一个取值范围。在此基础之上,需要设计电感Lf,Lg。首先分析逆变器的谐波源。针对图2所示的简化结构,逆变器侧的电压如式(9)所示:

式中:S(t)是开关函数,其随时间变化而变化,根据参考文献[6]可以得到,开关函数如下:

上式中,第一项是基波部分,第二项是高频部分,也是分析的重点,定义其如下:
根据参考文献[6]中的赛贝尔公式,当n为奇数时候,式(11)可变为:
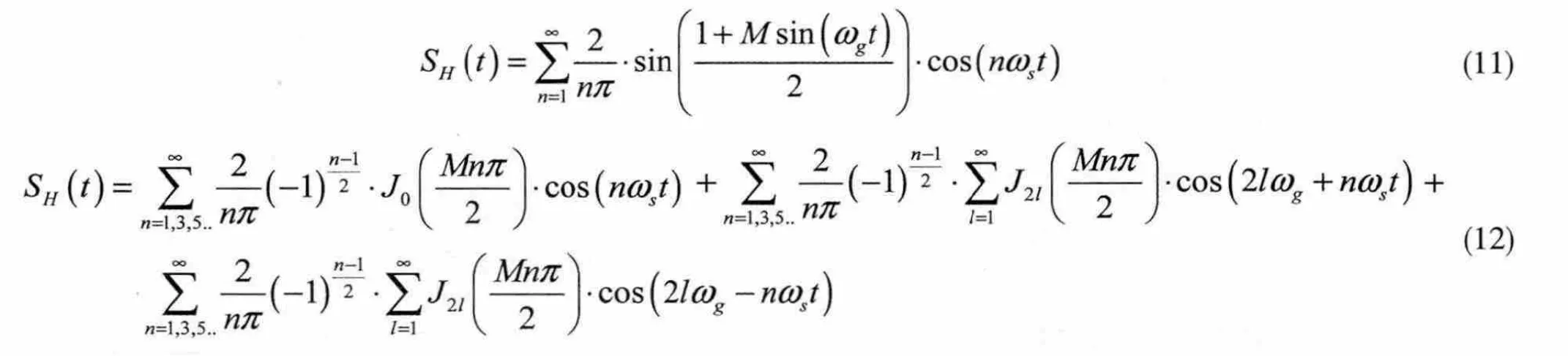
从频率角度看,谐波的频率点为:
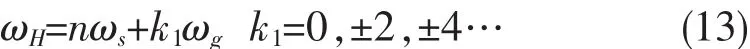
谐波频率处的谐波幅值为:
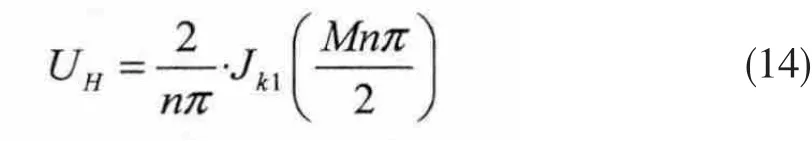
当n为偶数时候,式(11)可变为:
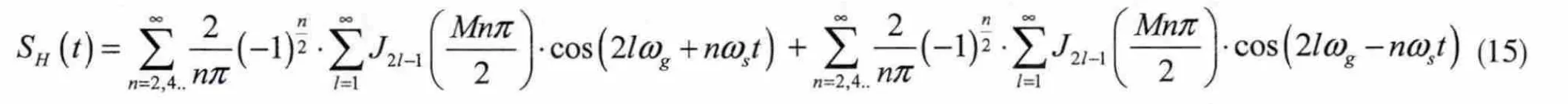
同样,从频率的角度,谐波频率和对应的幅值分别为:

式(14)、(17)是相对于基波含量,由此可以得到各个谐波含量值,即可得总谐波含量:

由此可以看出,谐波含量只与系统的调制度M有关系。
通过上述分析可以计算得出主要频率点上的谐波量,在一般考虑中,计算相对于基波的各个谐波含量如图4所示。
通过上述分析可以得知,该种计算方法和仿真结果一致,证明分析方法的正确性。
1.3 成本方面
LCL滤波器的主要组成元器件为电感和电容,通常情况下,电感的成本会高于电容的成本,因此,在达到相同滤波效果时,通常会增大电容,减小电感,以降低成本,所以电感设计时一般选择两个电感之和较小值。同时,Lf和Lg两个电感值越接近,相对于单个感量相同的所需磁路材料略少,成本略低。但是由于两个电感均衡设计,总体积增加,在设计时需要折中考虑。
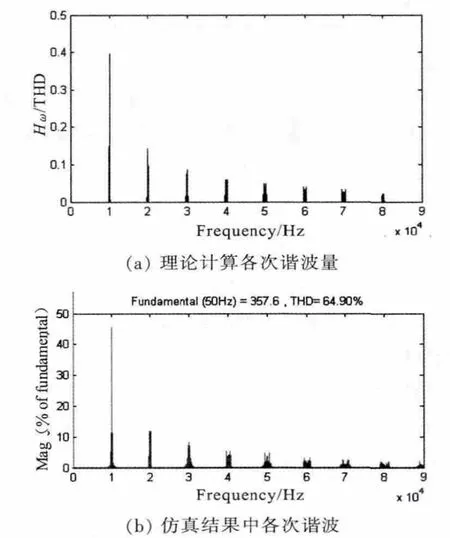
图4 各次谐波含量
1.4 控制系统设计方面
滤波器设计时,存在谐振频率和系统的截止频率,在实际设计时,一般要求截止频率满足式(19)[2],以保证控制系统设计的合理性。

2 LCL滤波器参数设计
根据前节的分析,滤波器的设计过程主要考虑纹波电流量、谐波量,参考成本因素及控制的难易性,经过多次优化最终得到优化的电抗器。本文以表1所示100 kW三电平逆变器为应用场合,对LCL滤波器参数进行设计。
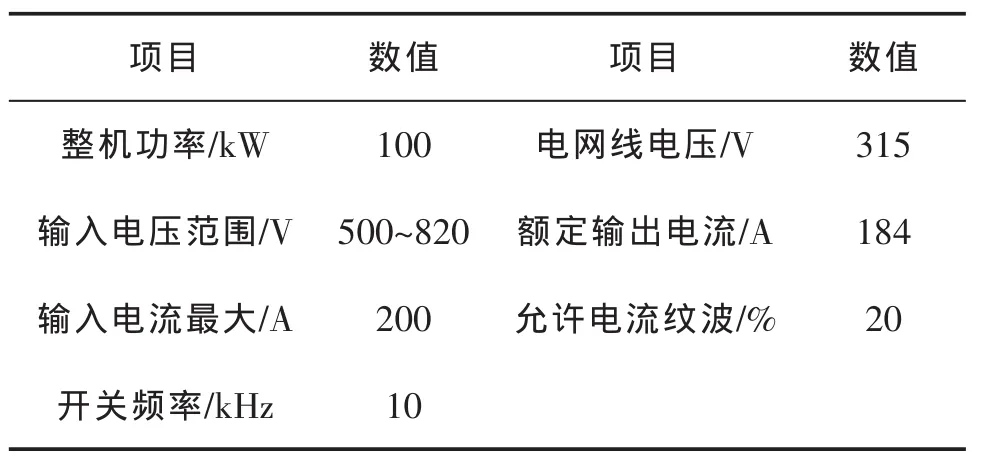
表1 逆变器参数
2.1 纹波设计
根据100 kW三电平逆变器参数表中纹波电流要求可知,输出电流有效值Irms=184 A。由此可得纹波电流最大为:

将式(8)代入(18),代入表中数据可得:

为了降低成本,因此选择Lf=0.23 mH允许纹波电流值为ΔI=51 A。
2.2 谐波设计
LCL滤波器滤除高频谐波的基本原理是通过支路的阻抗匹配,从而使高频谐波电流被电容吸收。
根据参考文献[2]当系统全部输入无功时,电容数值如下:
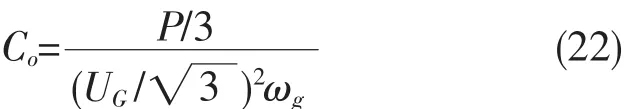
实际系统针对逆变器允许无功量的要求,设定输出电容系数r。

设L是前个电感Lf和Lg的总的电感量,即满足:

设定,Lf是Lg的a倍[7],则在频率ω处的阻抗分别为:

根据滤波器滤除谐波的原理,假设在频率ω处电流注入电网电流是总Iω的λ倍,即:

根据基尔霍夫定律,满足上述可得:
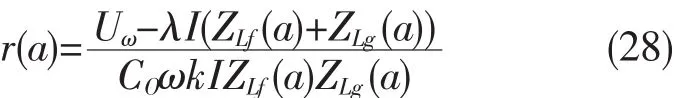
根据一般经验,中开关频率处谐波含量和总谐波含量的关系,要保证THD≤3%,一般保证开关频率处谐波含量小于2%。因此,上述分析中可以代入ω=ωs,λ=0.02,可以得到的 r随 k 的函数曲线如图所示。
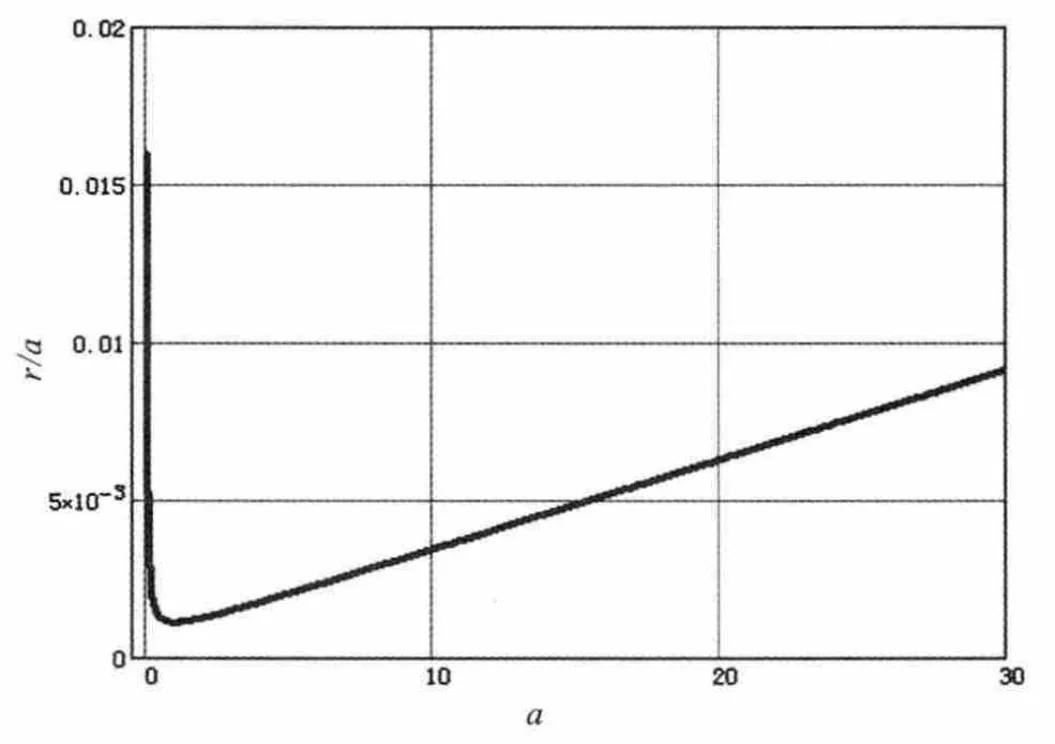
图5 电容系数和电感系数关系
图5 所述曲线是满足既定λ=2%的临界曲线,要想满足λ<2%则需要取曲线上方的取值。
根据上述分析,综合考虑体积、成本和谐振频率,选择 a=20,r=0.01,由此可见余量足够。由式(19)~(26) 可得:Cf=30 μF,Lf=230 μH,Lg=11.5 μH,由于设计网侧电抗比较小,实际系统中,Lg采用线缆电感、升压变压器漏感的作用来实现。
2.3 工作状态校核
根据参考文献[2],LCL滤波器的谐振频率为:
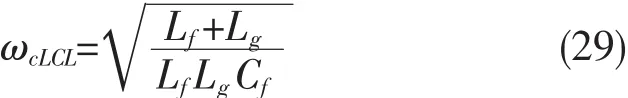
LC滤波器的谐振频率为:

LCL滤波器中当Lg取值很小时,可以看做是LC滤波器。本设计中由于Lg的取值很小,为线缆电感,因此滤波器表现为LC滤波器特点,即将设计结果及系统参数代入式(30),可知,ωc=1.16×104rad/s≈0.185 ωs,满足控制方面设计要求,给系统控制参数设计的带来方便。
3 仿真结果
针对上述设计,利用MATLAB/Simulink中强大的仿真功能,对上述100 kW三电平逆变器设计参数进行仿真验证。其参数与表1参数一致。仿真的纹波和THD分别如图6、图7所示。
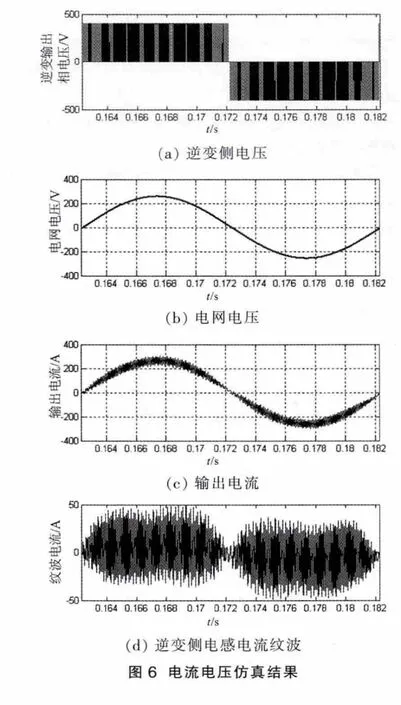
从仿真结果可以看出,图 6(c)、(d)与图 3(b)、(a)中所示分析结果一致,纹波电流最大值控制为50 A,与设计值一致。

图7 谐波仿真结果
由于滤波器设计过程中电感、电容取值保留余量,因此开关频率处的谐波量相对于基波含量为1%,比设计值低,同时THD是2.35%,满足设计要求。
4 实验验证
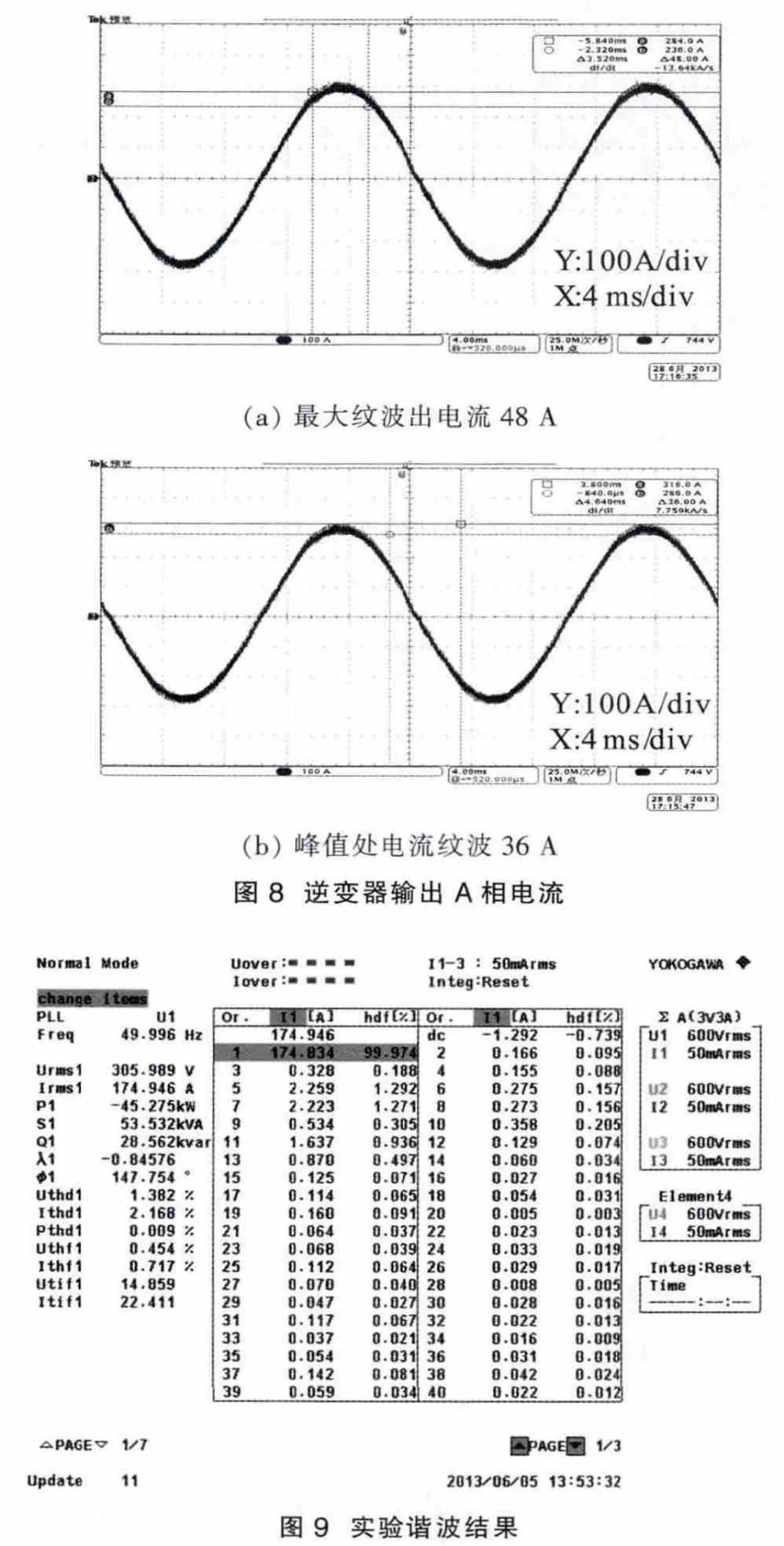
本文在100 kW的实验平台对所设计电抗谐波和纹波电流进行了实验验证。电流纹波波形如图8所示,与图6(c)所示波形一致。在实验中测得输出电流为198 A时,由于示波器无法直接测量纹波电流,因此只能在电流波形中测量纹波电流值,其最大纹波48 A,在电流峰值处电流纹波36 A,由于实际系统中线缆电抗的存在会导致实际值比理论值偏小。
在谐波测试方面,在174.9 A输出电流时,使用YOKOGAWA品牌WT3000功率分析仪测得THD为2.168%,如图9所示。由于测试仪器局限性,该仪器只测试到相对基波100次谐波,并对其计算谐波,尚未测试全部谐波,因此数值相对仿真值偏小。
5 总结
本文从纹波电流、谐波、成本和系统控制等方面出发,对LCL滤波器的设计进行了深入的研究,提出了一种光伏并网逆变器的LCL滤波器的设计方法。针对100 kW三电平光伏并网逆变器的应用,通过纹波电流及谐波源的分析,详细设计了逆变器的LCL滤波器,以满足电网对电能质量的要求。仿真结果表明,所设计的滤波器效果与设计结果一致,仿真和实验验证了设计方法的正确性和合理性。该设计方法作为一种通用设计方法,可为同领域的设计人员进行产品设计时提供有力的参考。
[1]Min-Young Park,Min-Hun Chi.LCL-filter Design for Grid-Connected PCS Using Total Harmonic Distortion and Ripple Attenuation Factor[C].The 2010 International Power Electronics Conference,1688-1694。
[2]Fei Liu,Xiaoming Zha.Design and Research on Parameter of LCL Filter in Three-Phase Grid-Connected Inverter[C].Power Electronics and Motion Control Conference,2009:2174-2177.
[3]C T Wang,Z Ye.Output Filter Design for a Grid-Interconnected Three-Phase Inverter[C].Power Electronics Specialist Conference,2003(2):779-784.
[4]袭景斌,周维来.双馈风电变流器网侧LCL滤波器设计[J].节能与新能源,2009(6):44-46.
[5]中华人民共和国国家标准GB/T 14549-1993.电能质量公用电网谐波[S].
[6]马伟明,张磊.独立电力系统及其电力电子装置的电磁兼容[M].北京:科学出版社.
[7]Marco Liserre,Frede Blaabjerg.Design and Control of an LCL-Filter-Based Three-Phase Active Rectifier[J].TRANSACTIONS ON INDUSTRY APPLICATIONS,VOL.41,NO.5,1281-1291.

